El color de la luna y el sol desde el espacio en los valores de RGB y temperatura de color.

Parece que la cuestión del color de la Luna y el Sol desde el espacio es tan simple para la ciencia moderna que en nuestro siglo no debería haber ningún problema con una respuesta. Estamos hablando de colores cuando se observan con precisión desde el espacio, porque la atmósfera conduce a un cambio de color debido a la dispersión de luz de Rayleigh. "Seguramente en algún lugar de la enciclopedia sobre esto en detalle, en números se ha escrito durante mucho tiempo", dice. Bueno, ahora mismo, intente buscar en Internet esta información. ¿Funcionó? Lo más probable es que no. Lo máximo que encontrarás es un par de palabras de que la luna tiene un tinte marrón y el sol es rojizo. Pero no encontrará información sobre si estos tonos son visibles para el ojo humano o no, especialmente los valores de los colores en RGB o al menos las temperaturas de color. Pero luego encontrará un montón de fotos y videos donde la Luna desde el espacio se muestra absolutamente gris, principalmente en las fotografías del programa estadounidense Apollo, y donde el Sol desde el espacio se muestra en blanco e incluso azul.

Mi opinión puramente personal no es más que una consecuencia de la interferencia de la política en la ciencia. Después de todo, los colores de la Luna y el Sol desde el espacio se relacionan directamente con los vuelos de los estadounidenses a la Luna.

Busqué en muchos artículos y libros científicos en busca de información sobre el color de la luna y el sol desde el espacio. Afortunadamente, resultó que a pesar de que no tienen una respuesta directa en RGB, hay información completa sobre la densidad espectral de la radiación solar y la reflectividad de la luna en el espectro. Esto es suficiente para obtener los colores exactos en los valores RGB. Solo necesita calcular cuidadosamente lo que, de hecho, hice. En este artículo compartiré los resultados de los cálculos con usted y, por supuesto, le contaré en detalle sobre los cálculos mismos. ¡Y verás la luna y el sol desde el espacio en colores reales!

Realicé los cálculos en el programa Mathcad y, en consecuencia, los fragmentos de código estarán en el lenguaje de programación incorporado, que es bastante adecuado como un pseudocódigo que es comprensible para todos.

Al mismo tiempo, le diré en detalle cuál es el modelo de color RGB, con el cual, creo, todos están familiarizados. Esta pregunta tampoco es del todo simple. Por ejemplo, intente responder las siguientes dos preguntas. Deje que se le dé el color rgb (120,80,100) .
1) ¿Cuáles son los valores del color RGB, que es 2 veces más oscuro que el especificado?
2) ¿Cuáles son los valores RGB para el gris que tienen el mismo brillo que el dado?
Parece que lo que hay que pensar, se divide por 2 en el primer caso, es decir, rgb (60,40,50) y promedio en el segundo caso, es decir, rgb (100,100,100) . Por desgracia, las respuestas correctas son: 1) rgb (86.56.71) ; 2) rgb (92.92.92) . Descubrirá por qué las respuestas son solo eso.

También hablaré sobre la temperatura del color y cómo calcularlo.

Espacio de color XYZ

XYZ es un modelo de color de referencia definido en el estricto sentido matemático por CIE (Comisión Internacional de Iluminación) en 1931. El modelo CIE XYZ es un modelo maestro de casi todos los demás modelos de color utilizados en campos técnicos. El color XYZ se establece de la siguiente manera:

$$

$$X = \ int _ {390 \, nm} ^ {830 \, nm} I (\ lambda) \, {\ overline {x}} (\ lambda) \, d \ lambda \\ Y = \ int _ { 390 \, nm} ^ {830 \, nm} I (\ lambda) \, {\ overline {y}} (\ lambda) \, d \ lambda \\ Z = \ int _ {390 \, nm} ^ { 830 \, nm} I (\ lambda) \, {\ overline {z}} (\ lambda) \, d \ lambda$$

donde $$$I (\ lambda)$ - densidad espectral de cualquier cantidad fotométrica de energía (por ejemplo, flujo de radiación, brillo de energía, etc., en términos absolutos o relativos) en el rango de longitud de onda de 390 a 830 nm (esto según 2006, en 1931 el rango era de 380 a 780 nm ); $$${\ overline {x}} (\ lambda)$ , $$${\ overline {y}} (\ lambda)$ , $$${\ overline {z}} (\ lambda)$ - funciones de coincidencia de color. Además, lo que es importante para nosotros, la coordenada Y corresponde al brillo visual de la señal.

Los datos de la función de coincidencia de color que descargué de aquí: [ 1 ]. Allí, las funciones de coincidencia de color se definen para el campo de visión de 2 y 10 grados . Decidí realizar cálculos para ambos casos, comparar los resultados y asegurarme de que, como se esperaba, las coordenadas de color difieren ligeramente. Naturalmente, utilicé estas funciones con la resolución máxima proporcionada, es decir, con un paso de 0.1 nm . Los gráficos de las funciones de coincidencia de color son los siguientes:



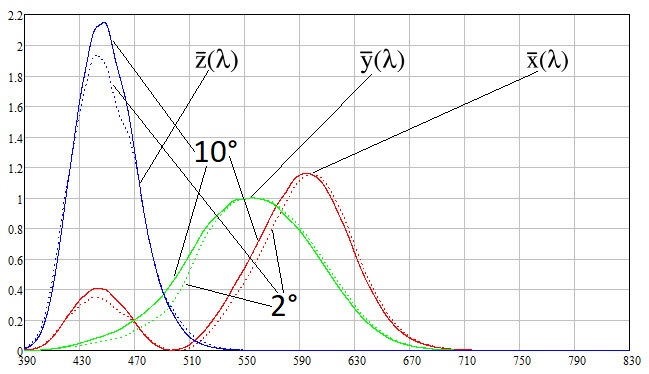
Los gráficos muestran que por encima de 710 nm las funciones se vuelven insignificantes en el sentido de que al observar un color cercano al blanco, la densidad espectral en el rango superior a 710 nm casi no contribuye. Aunque sabemos que la luz visible se encuentra en el rango de hasta 780 nm , debemos entender que esto es con radiación monocromática. Todo esto por el hecho de que en los cálculos tuve que extrapolar en algunos casos los datos faltantes de la luminosidad de la luna solo al rango donde las funciones de coincidencia de colores son esencialmente pequeñas. Por lo tanto, un posible error de extrapolación no conduce a un error notable en los colores calculados.

Calculo las integrales indicadas por el método trapezoidal :


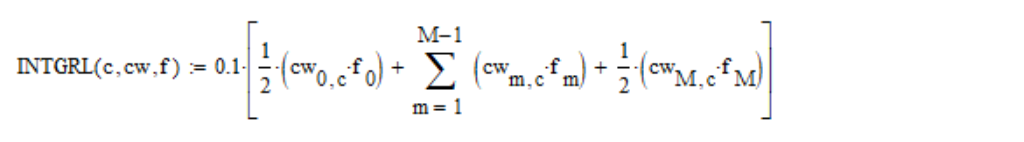
donde c es el número de coordenadas del espacio de color (1, 2, 3 para X, Y, Z, respectivamente); cw - tabla de funciones de coincidencia de color; f es la densidad espectral; M = (830-390) /0.1=4400: el número de pasos de la cuadrícula.

Las funciones de coincidencia de color correctas tienen la propiedad de que el área bajo las tres curvas es la misma:

$$

$$\ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {x}} (\ lambda) \, d \ lambda \, = \ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {y}} (\ lambda) \, d \ lambda \, = \ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {z}} (\ lambda) \, d \ lambda$$

Esto se hace para que el espectro uniforme tenga las mismas coordenadas XYZ. Compruebe si esta propiedad tiene:


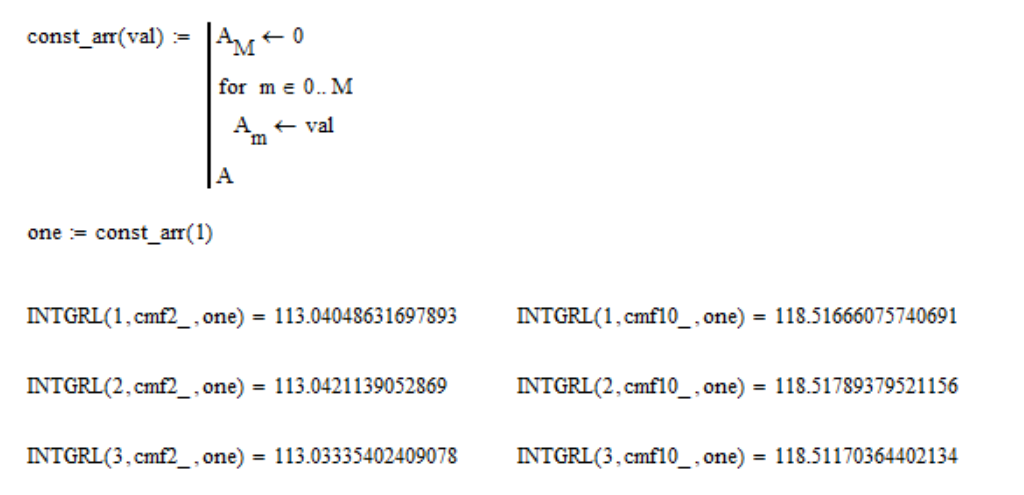
donde uno es una matriz de 1; cmf2_ y cmf10_ son tablas de funciones de coincidencia de color para el campo de visión de 2 y 10 grados , respectivamente. Como puede ver, la propiedad está satisfecha con una precisión del 0.01% , lo cual es muy bueno. Pero aún así, renormalizamos las funciones para la fidelidad:

Normalización de brillo

Considere la operación de una cámara digital. El elemento principal de una cámara digital es una matriz, que consiste en fotosensores. Al proyectar una imagen en una matriz, una carga eléctrica es proporcional a cada uno de sus fotosensores, que es proporcional a la energía de radiación del fotosensor. Los fotosensores capturan el brillo de un elemento de imagen sin ninguna información sobre su color. Para obtener información sobre el color, la matriz de fotosensores se cubre con una matriz de filtros de luz en miniatura en la parte superior. Estos filtros sirven como funciones de coincidencia de color. Cada píxel consta de varios fotosensores, que en total se superponen a todo tipo de filtros.

Entonces, como una función $$$I (\ lambda)$ Deberíamos tomar la densidad espectral de la energía de irradiación de un píxel. Tal densidad espectral se puede representar como

$$

$$I (\ lambda) = coef \ cdot iluminación (\ lambda) \ cdot albedo (\ lambda)$$

donde iluminación es la densidad de radiación espectral de la fuente de luz ; albedo - reflectividad de la superficie del objeto fotografiado; coef : cierto coeficiente constante, que está determinado por el tiempo de exposición, la apertura, la distancia desde la fuente de luz hasta el objeto fotografiado y otros factores. La reflectividad se refiere al albedo aparente , que se define como la relación entre el brillo de un elemento de superficie plana iluminado por un haz de rayos paralelo al brillo de una superficie completamente blanca perpendicular a los rayos.

Ahora imagine que estamos haciendo el trabajo de un medidor de exposición de fotos, con el cual el fotógrafo establece la velocidad de obturación y la apertura de la cámara. En otras palabras, debemos elegir el valor del coeficiente para que la imagen resulte normal en brillo, ni demasiado oscura ni demasiado brillante. Imagine que detrás del objeto fotografiado hay una pantalla completamente blanca. El albedo de reflectancia de dicha pantalla es, por definición, igual a 1 en todas las longitudes de onda. Establezca el valor de coef de modo que el brillo visual Y de esta pantalla en la imagen sea 1. ¿Por qué 1? Porque en el modelo de color RGB, el valor de brillo máximo posible es 1, que se logra con rgb (255,255,255) , es decir, con color blanco. Hablaré de esto más tarde. Dado que los cuerpos ordinarios son de color más oscuro que una pantalla completamente blanca, las imágenes tendrán un brillo normal. De estas consideraciones, obtenemos la siguiente expresión para coef :

$$

$$coef = \ frac {1} {\ int _ {390 \, nm} ^ {830 \, nm} iluminación (\ lambda) \, {\ overline {y}} (\ lambda) \, d \ lambda}$$

Cabe señalar que tal normalización no garantiza que el valor de cada coordenada RGB sea menor o igual a 255. Por ejemplo, si dispara una pantalla absolutamente blanca con una fuente de luz roja, el color RGB se disparará.

Entonces, calculo las coordenadas del espacio de color XYZ de la siguiente manera:


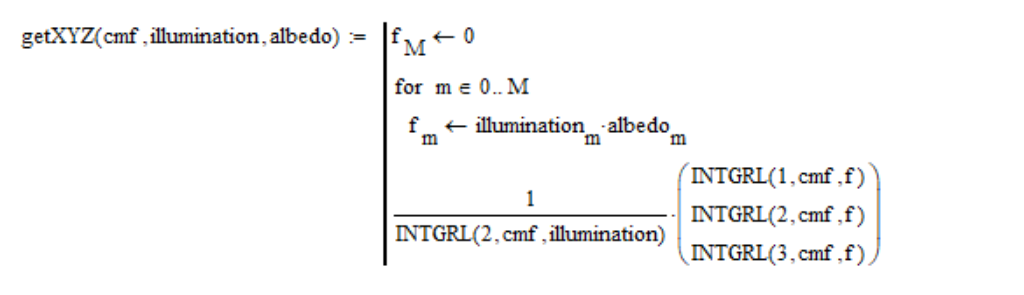
Necesitamos de alguna manera expresar el color del sol. No podemos fotografiarlo directamente, y en nuestro modelo matemático no proporcionamos un caso tan extremo. Obviamente, necesitamos fotografiar la superficie blanca iluminada por el Sol. Como el Sol del espacio exterior tiene un tono rojizo, entonces, como dije, el color de una pantalla absolutamente blanca se sale de escala. Por lo tanto, debemos tomar la superficie más oscura. Experimentalmente descubrí que necesitas tomar papel blanco con un albedo de 0.91. No puedes tomar más albedo, comienza a darse vuelta. Por lo tanto, para obtener el color del Sol, simplemente configuré el valor del albedo en 0.91 en todas las longitudes de onda en la fórmula anterior:

Espacio de color SRGB

El espacio de color más común que usa el modelo RGB es sRGB. Por lo tanto, cuando se habla de RGB sin aclaración, se refieren al espacio de color sRGB, que es el estándar para representar el espectro de color utilizando el modelo RGB. Este estándar fue creado por el International Color Consortium (ICC) en 1996 para unificar el uso del modelo RGB en monitores, impresoras y sitios de Internet. Miremos este estándar, cuya descripción está disponible en [ 2 ].

La conversión de XYZ a sRGB tiene lugar en tres etapas. Primero, las coordenadas XYZ se convierten en coordenadas RGB lineales, luego las coordenadas lineales se convierten en coordenadas RGB no lineales y finalmente las coordenadas no lineales se convierten en coordenadas RGB de 8 bits, que, de hecho, son las coordenadas del espacio de color sRGB.

La conversión de coordenadas XYZ a coordenadas RGB lineales es la siguiente:



y lo contrario es así:



Me pregunto de dónde vienen estos extraños números en matrices cuadradas. Y vinieron de la recomendación ITU-R BT.709 [ 3 ]. Denote la primera matriz cuadrada por XYZ_to_RGB , y la segunda por RGB_to_XYZ . Obviamente, son mutuamente inversos. La Recomendación UIT-R BT.709 especifica los requisitos que deben cumplirse para la segunda matriz. A partir de estos requisitos, podemos calcular de manera única la segunda matriz, y la primera es igual a la matriz inversa de la segunda.

Presentamos las siguientes funciones:

$$

$$XYZ (R, G, B) = RGB \ _to \ _XYZ \ cdot {\ begin {bmatrix} R \\ G \\ B \ end {bmatrix}} \\ W (R, G, B) = XYZ_1 (R , G, B) + XYZ_2 (R, G, B) + XYZ_3 (R, G, B) \\ xy (R, G, B) = \ frac {1} {W (R, G, B)} \ cdot {\ begin {bmatrix} XYZ_1 (R, G, B) \\ XYZ_2 (R, G, B) \ end {bmatrix}}$$

Luego, los requisitos de la recomendación UIT-R BT.709 toman la siguiente forma:

$$

$$xy (1,0,0) = {\ begin {bmatrix} 0.64 \\ 0.33 \ end {bmatrix}}, \; xy (0,1,0) = {\ begin {bmatrix} 0.30 \\ 0.60 \ end {bmatrix}}, \; xy (0,0,1) = {\ begin {bmatrix} 0.15 \\ 0.06 \ end {bmatrix}} \\ xy (1,1,1) = {\ begin {bmatrix} 0.3127 \\ 0.3290 \ end {bmatrix }}$$

Tenemos 8 ecuaciones cuando tenemos 9 elementos desconocidos de la matriz RGB_to_XYZ , es decir, falta una ecuación más. Y la ecuación faltante se estableció implícitamente, tuve que adivinarlo yo mismo. La esencia de esta ecuación es que para el blanco, el brillo visual Y debería ser igual a 1:

$$

$$XYZ_2 (1,1,1) = 1$$

Encontré la solución exacta a estas ecuaciones en números racionales:


Si redondeo los números en mi resultado a cuatro decimales, entonces obtenemos exactamente esos números muy extraños en el estándar del International Color Consortium. En mis cálculos, uso matrices no redondeadas, sino las exactas anteriores (en la medida en que lo permitan los números de coma flotante de precisión doble ).

Entonces, las coordenadas lineales de RGB basadas en la tabla de funciones de coincidencia de color (cmf), densidad de radiación espectral (iluminación) y reflectancia (albedo) calculo de la siguiente manera:



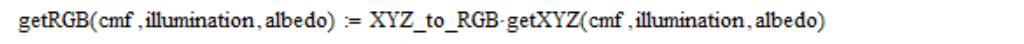
También uso coordenadas RGB lineales, promediadas en un campo de visión de 2 y 10 grados :



A partir de las coordenadas lineales de RGB, el brillo visual Y se calcula utilizando la siguiente fórmula (de manera predeterminada, las matrices de Mathcad están numeradas desde el elemento cero):


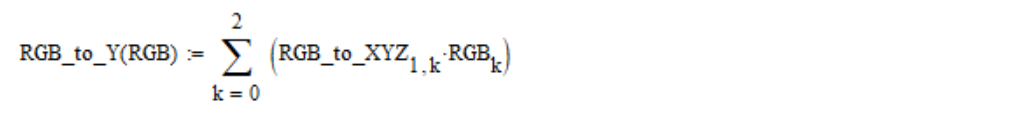
Seguimos desmontando el estándar. Cada coordenada RGB lineal se convierte en no lineal utilizando la función no lineal de lin2bit y viceversa, bit2lin, que se definen de la siguiente manera:


Los gráficos de estas funciones se ven así:



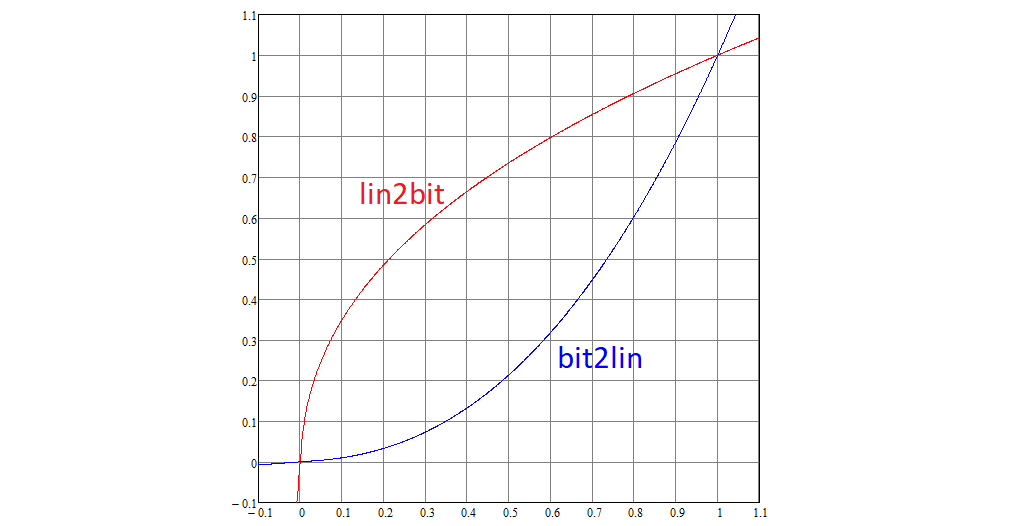
Tenga en cuenta que 0 se convierte en 0, 1 en 1.

Al final, las coordenadas RGB no lineales se convierten a 8 bits multiplicando por 255, seguido de redondeo a enteros.

Por lo tanto, he definido las siguientes funciones para convertir coordenadas RGB lineales a 8 bits y viceversa:

Ahora estamos listos para resolver el problema desde la introducción. Te recuerdo la condición.

Deje que se le dé el color rgb (120,80,100) .
1) ¿Cuáles son los valores del color RGB, que es 2 veces más oscuro que el especificado?
2) ¿Cuáles son los valores RGB para el gris que tienen el mismo brillo que el dado?

Solución:

Respuestas: 1) rgb (86.56.71) ; 2) rgb (92.92.92) .

Temperatura de color

La temperatura de color de la fuente de luz, medida en Kelvin, está determinada por la temperatura de un cuerpo completamente negro ubicado en la tabla de colores en el mismo lugar que la fuente de radiación en cuestión. Si la fuente de luz no cae en la curva de Planck (una curva que está determinada por el conjunto de puntos de color de un cuerpo negro a diferentes temperaturas), se utiliza una temperatura de color correlacionada para caracterizarla. Este valor también se mide en Kelvin y está determinado por la temperatura de un cuerpo completamente negro, cuyo color es lo más cercano posible al color de la fuente de luz. Para encontrar la temperatura de color correlacionada de la fuente de radiación en la tabla de colores construida en las coordenadas (u, v) , se determina el punto más cercano a la fuente en la curva de Planck (es decir, la distancia geométrica más corta). La temperatura del cuerpo negro ubicado en este punto corresponderá a la temperatura de color correlacionada de la fuente considerada [ 4 ].

Para un cuerpo completamente negro de temperatura T, la ley de Planck expresa la potencia de radiación por unidad de área de la superficie radiante en un intervalo de longitud de onda unitaria:

$$

$$R (\ lambda, T) = \ frac {2 \ pi h c ^ 2} {\ lambda ^ 5} \ frac {1} {e ^ {h c / \ lambda k T} -1}$$

En consecuencia, calculo la densidad de radiación espectral de un cuerpo absolutamente negro de la siguiente manera (en la columna cero de la tabla de funciones de coincidencia de colores cmf2 hay longitudes de onda en nanómetros):



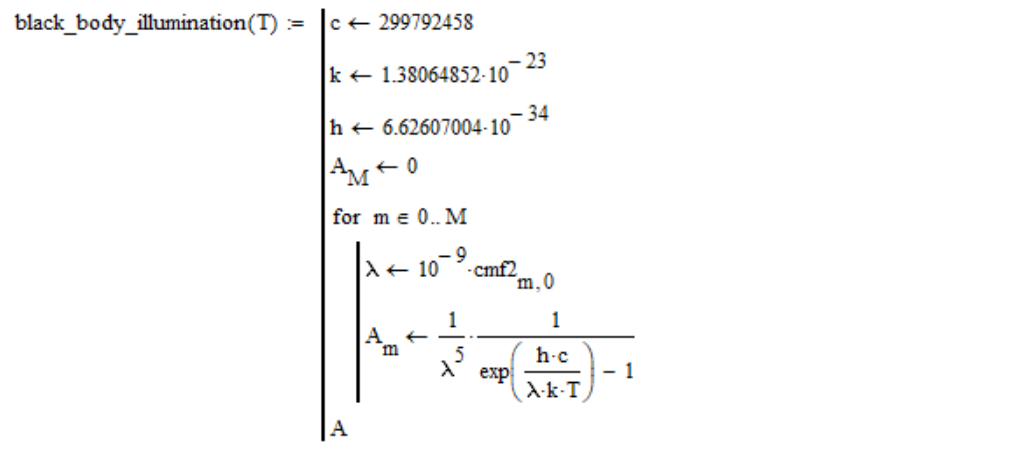
Tenga en cuenta que omití el factor constante, porque todavía disminuye con una mayor normalización por el brillo (el brillo de la fuente de luz no afecta la temperatura del color).

A continuación, calculo las coordenadas lineales de RGB:



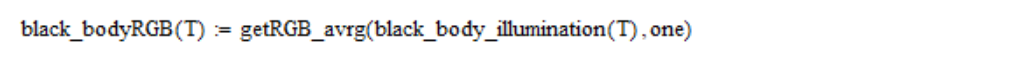
Las coordenadas lineales RGB se convierten en coordenadas (u, v) de la siguiente manera:



En el plano (u, v), se calcula la distancia geométrica entre los puntos del color en cuestión y el color del cuerpo negro de una temperatura T dada:



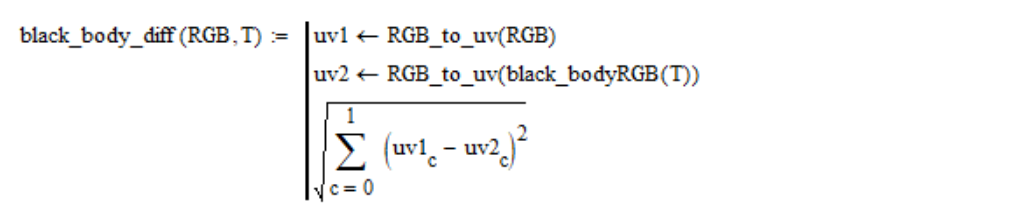
Por ejemplo, para una fuente de luz blanca estándar, la dependencia de esta distancia de la temperatura se ve así:



El valor de T al cual esta dependencia tiene un mínimo es la temperatura de color de la fuente de luz en cuestión.

La densidad espectral de la radiación del sol.

Descargué los datos de la densidad espectral de la radiación solar en ausencia de la atmósfera desde aquí: [ 5 ]. La fuente de luz correspondiente al Sol desde el espacio, en adelante la designaré como E490. Además, a modo de comparación, en los cálculos considero la fuente de luz estándar D65 . Esta fuente representa la luz blanca. Lo miro para mostrar cómo se vería la luna si el sol fuera blanco. Descargué los datos de la densidad espectral de radiación de una fuente de luz estándar D65 desde aquí: [ 6 ].

Como se mostrará a continuación, las fuentes de luz D65 y E490 tienen temperaturas de color de 6467K y 5912K, respectivamente. Las densidades de radiación espectral de las fuentes de luz D65, E490 y cuerpos absolutamente negros de las temperaturas correspondientes son las siguientes:



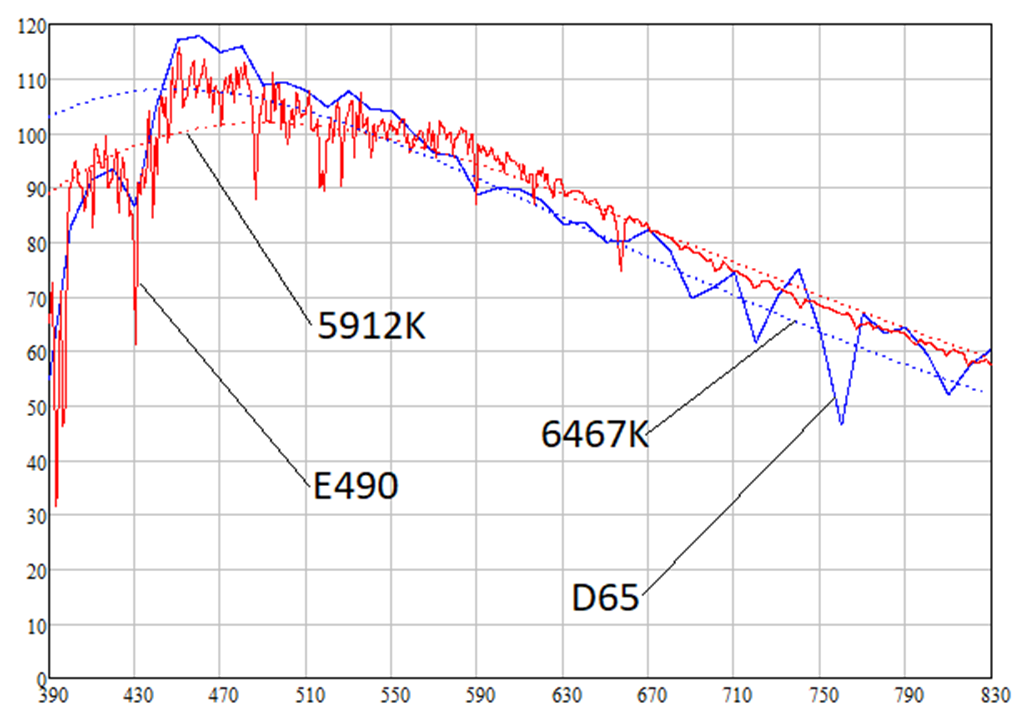
Se puede observar que la densidad espectral de la radiación solar es mayor que la de una fuente de luz blanca en longitudes de onda más largas, es decir, en longitudes de onda de luz roja (620-770 nm). Esto significa que el sol tiene un tinte rojizo. De hecho, los cálculos dan los siguientes colores de las fuentes de luz D65, E490 y cuerpos absolutamente negros de las temperaturas correspondientes (como dije, se considera papel blanco con un albedo de 0.91):



Tenga en cuenta que las coordenadas sRGB del Sol y la temperatura absoluta del cuerpo negro 5912K coinciden exactamente. Esto no se explica por nada, simplemente sucede.

El color de los círculos en la última imagen es el color real del Sol desde el espacio. El ojo humano ve claramente el tinte rojizo del sol. ¡Entonces, el hecho de que el Sol desde el espacio es blanco es un gran mito! Cabe señalar que, por alguna razón, este tono no se observa en las fotografías y el video del programa Apollo. En estas fotografías, el tono rojizo visible del Sol ciertamente aparecería en las superficies blancas de la bandera estadounidense y los trajes espaciales. Y como se mostrará a continuación, esta sombra del Sol hace una contribución notable al "enrojecimiento" de la Luna desde el espacio.

¿Es la luna diferente o igual en color?

Los opositores a la teoría de la conspiración lunar están promoviendo la versión de que la luna es de color diferente. Supuestamente en lugares donde la luna es gris, en lugares donde es marrón, y al mismo tiempo el Apolo aterrizó donde la luna es gris. Pero esta versión contradice directamente los datos científicos. El artículo [ 7 ] dice explícitamente:

Las diferencias de color en la luna son extremadamente pequeñas.

Shevchenko también escribe en su libro [ 8 ]:

Durante muchos años, el famoso investigador estadounidense T. McCord trabajó en esta dirección.Obtuvo más de 200 espectros para varias secciones de la superficie lunar que miden de 10 a 20 km cada una. Todas las curvas obtenidas son básicamente similares en apariencia.

Entonces, no, la luna no es diferente en color, sino igual.

Datos de color de la luna según Shevchenko

Shevchenko en su libro [ 8 ] da la siguiente dependencia de la reflectividad en la longitud de onda.



En mis cálculos, uso la interpolación lineal por partes de estos datos. Recibí los datos faltantes en el rango de 820–830 nm por continuación directa del intervalo en el rango de 690–820 nm.

Datos de color de luna por LRO

La dependencia de la reflectividad de la superficie lunar de las condiciones de iluminación y observación a longitudes de onda de 321 nm a 689 nm se da en [ 9 ]. Los parámetros del modelo se calcularon en base al análisis de los datos obtenidos por el Orbitador de Reconocimiento Lunar (LRO abreviado). Las condiciones de iluminación y observación están determinadas por tres parámetros i (ángulo de incidencia), e (ángulo de reflexión) yg (ángulo de fase). Estos ángulos se muestran en el siguiente diagrama:



El ángulo de fase se puede expresar en términos del ángulo azimutal$$Ψ utilizando elteorema del coseno esférico de lasiguiente manera:$\varPsi$

$$

$$g=\arccos\left(\cos\left(i\right)\cos\left(e\right)+\sin\left(i\right)\sin\left(e\right)\cos\left(\varPsi\right)\right)$$

En los cálculos, tomo los valores tradicionales de los ángulos i = g = 30 °, e = 0 °. Para tales ángulos, se obtiene la siguiente dependencia de la reflectancia en la longitud de onda (gráfico lro30):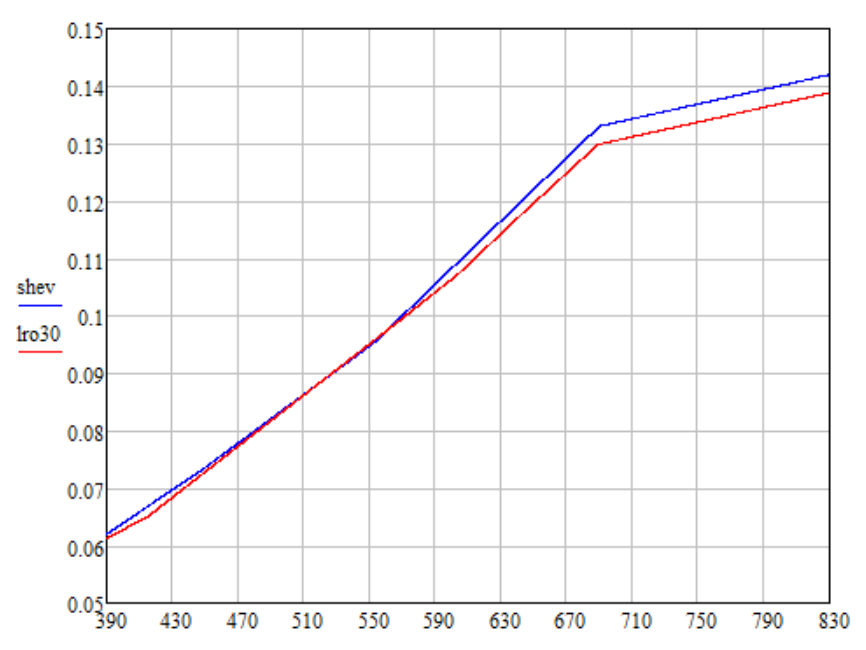


realicé una extrapolación lineal de los datos LRO al intervalo 689-830 nm para que la relación de los valores en los puntos 830 nm y 689 nm fuera la misma que la de los datos de Shevchenko ( horario shev). También renormalicé los datos de Shevchenko multiplicando por 0.8315 para que el brillo de los cálculos de color resultantes según Shevchenko y LRO fueran los mismos.

Información de color para la luna por Kaguya

El trabajo [ 10 ] presenta datos obtenidos por el segundo satélite japonés de luna artificial. Desafortunadamente, la reflectividad en el rango de longitud de onda visible se da con una resolución muy baja, por lo que no la uso en mis cálculos.

Pero el trabajo es interesante porque habla sobre las colosales discrepancias de los datos de Kaguya con los datos de la misión Apolo 16. Y este es uno de los raros casos en que la comunidad científica habla abiertamente de inconsistencias asociadas con los vuelos de los estadounidenses a la luna.

Resultados de calculo

Además, usaré la siguiente notación:
D65 : una fuente estándar de luz blanca D65;
E490 - fuente de luz del Sol en ausencia de atmósfera;
B-0.91 - papel blanco con un albedo de 0.91;
LRO (30 °) : datos de LRO para ángulos tradicionales i = g = 30 °, e = 0 °;
Shevch - datos sobre Shevchenko;
ling. (2 °) - coordenadas lineales RGB en un campo de visión de 2 grados ;
ling. (10 °) - coordenadas lineales RGB en un campo de visión de 10 grados ;
ling. (promedio) - coordenadas lineales RGB promediadas sobreCampo de visión de 2 grados y 10 grados ;
sRGB (100%) : coordenadas sRGB obtenidas de coordenadas RGB lineales promediadas en un campo de visión de 2 y 10 grados ;
sRGB (200%) : coordenadas sRGB obtenidas de coordenadas RGB lineales duplicadas promediadas en un campo de visión de 2 grados y 10 grados ;
sRGB (300%) : coordenadas sRGB obtenidas de coordenadas RGB lineales triplicadas promediadas en un campo de visión de 2 grados y 10 grados ;
sRGB (400%) : coordenadas sRGB obtenidas de coordenadas RGB lineales cuádruples promediadas sobreCampo de visión de 2 grados y 10 grados ;
col. ritmo - temperatura de color obtenida de coordenadas RGB lineales promediadas en un campo de visión de 2 grados y 10 grados ;

D65

	B-0.91	LRO (30 °)	Shevch
ling. (2 °)	0.9076,0.9120,0.8968	0.1177,0.0931,0.0688	0.1202,0.0931,0.0697
ling. (10 °)	0.9084,0.9122,0.8929	0.1165.0.0916.0.0687	0.1188,0.0917,0.0696
ling. (promedio)	0.9080,0.9121,0.8948	0.1171,0.0924,0.0688	0.1195,0.0924,0.0697
sRGB (100%)	rgb (244,245,243)	rgb (96.86.74)	rgb (97.86.75)
sRGB (200%)	-	rgb (133,119,104)	rgb (134,119,104)
sRGB (300%)	-	rgb (160,144,125)	rgb (161,144,126)
sRGB (400%)	-	rgb (182,164,143)	rgb (184,164,144)
col. ritmo	6467K	4928K	4891K

E490

	B-0.91	LRO (30 °)	Shevch
ling. (2 °)	1.0005,0.8892,0.8490	0.1283.0.0909.0.0649	0.1310,0.0909,0.0657
ling. (10 °)	1.0021,0.8888,0.8483	0.1272,0.0895,0.0650	0.1297,0.0895,0.0659
. (.)	1.0013,0.8890,0.8486	0.1277,0.0902,0.0649	0.1303,0.0902,0.0658
sRGB (100%)	rgb(255,242,237)	rgb(100,85,72)	rgb(101,85,73)
sRGB (200%)	-	rgb(138,118,101)	rgb(140,118,102)
sRGB (300%)	-	rgb(166,142,122)	rgb(168,142,123)
sRGB (400%)	-	rgb(189,162,139)	rgb(191,162,140)
. .	5912K	4550K	4512K

La siguiente imagen muestra los colores de la superficie lunar sRGB (100%) , sRGB (200%) (brillo doble), sRGB (300%) (brillo triple), sRGB (400%) (brillo cuádruple) con una fuente de luz E490 (p. Ej. tras la observación desde el espacio) según los datos de LRO y Shevchenko.



Como puede ver, la Luna desde el espacio tiene un color marrón, según LRO y Shevchenko. Por Shevchenko resulta un poco (apenas perceptible) más rojo que por LRO.

Color de la luna en fotos

En esta sección nos ocuparemos del color de las fotografías. Deje que la imagen img y el color en coordenadas lineales de RGB se den. Cada píxel de la imagen se reemplaza por un píxel de un color dado con el mismo brillo que el color del píxel original. La imagen en Mathcad se presenta como una matriz de coordenadas sRGB única, que se obtiene al unir las tres matrices "R", "G", "B" de izquierda a derecha. Con esto en mente, el procedimiento de coloración es el siguiente:

Por interés, tomé fotografías de la superficie lunar de los álbumes de fotos del programa estadounidense Apollo y las volví a pintar con los colores obtenidos de mis cálculos. Solo doy los resultados, pero llego a la conclusión de si estas fotos son genuinas o falsas, usted mismo.

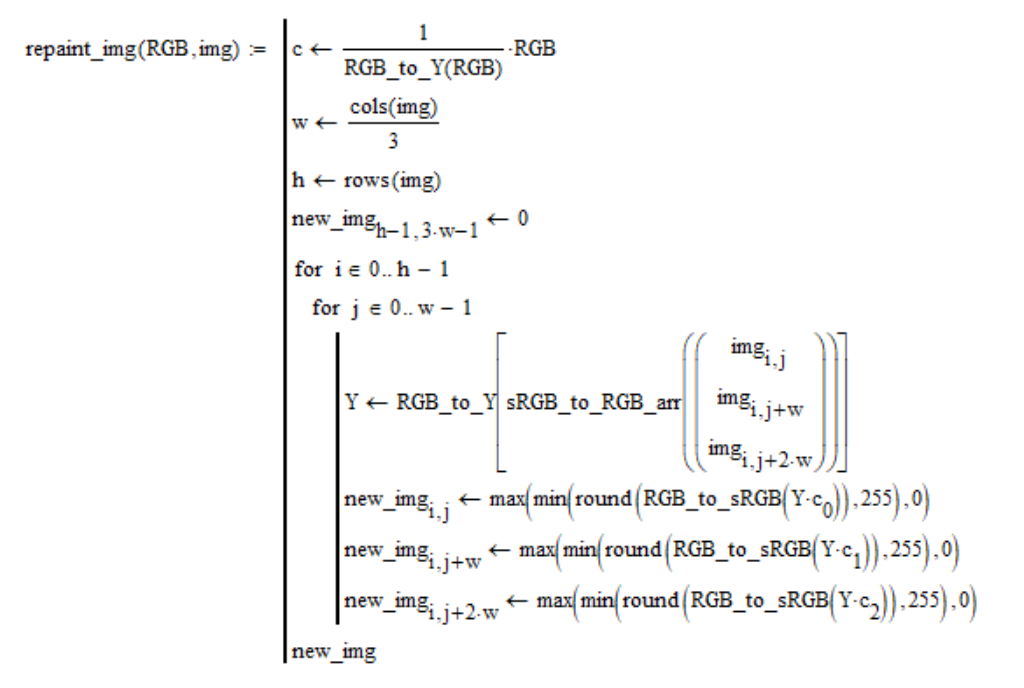
El resultado de colorear la foto AS11-44-6552 :



En el medio están las fotos originales. A la izquierda, las fotos se pintan en colores según los datos de LRO con ángulos tradicionales i = g = 30 ° , e = 0 ° , y a la derecha, según los datos de Shevchenko. La fila superior corresponde a la fuente de luz estándar D65, es decir, la fila superior muestra los colores de la superficie de la luna, que se habrían obtenido si el sol fuera blanco. La fila inferior corresponde a la fuente de luz E490, es decir, la fila inferior muestra los colores naturales de la superficie de la luna cuando se observa desde el espacio.

Como puede ver, el tono rojizo del Sol contribuye notablemente al "enrojecimiento" de la superficie de la Luna, que al final se ve marrón, no gris en absoluto.

El color gris de la Luna en las fotografías de la NASA podría explicarse por el hecho de que la película por alguna razón "se volvió" azul, pero esta versión desaparece inmediatamente si analizamos las imágenes de gradaciones grises al final de los álbumes. La foto como 11-44-chart muestra una imagen para la última foto de arriba. Dejé grises reales del mismo brillo a la izquierda de las gradaciones de gris con el mismo brillo que en la fotografía, y también anoté las coordenadas sRGB. El resultado es la siguiente imagen:



Como puede ver, la película no solo se ha "ido" al azul, sino que incluso se ha "ido" un poco en la dirección opuesta al azul. Tal desviación no puede convertir el marrón en gris.

El resultado de colorear la foto AS11-40-5903 :



En la fotografía original, la superficie lunar en algunos lugares no solo tiene un color gris, sino incluso un ligero tinte azulado. La foto del gráfico as11-40 muestra la imagen de gradación gris correspondiente:



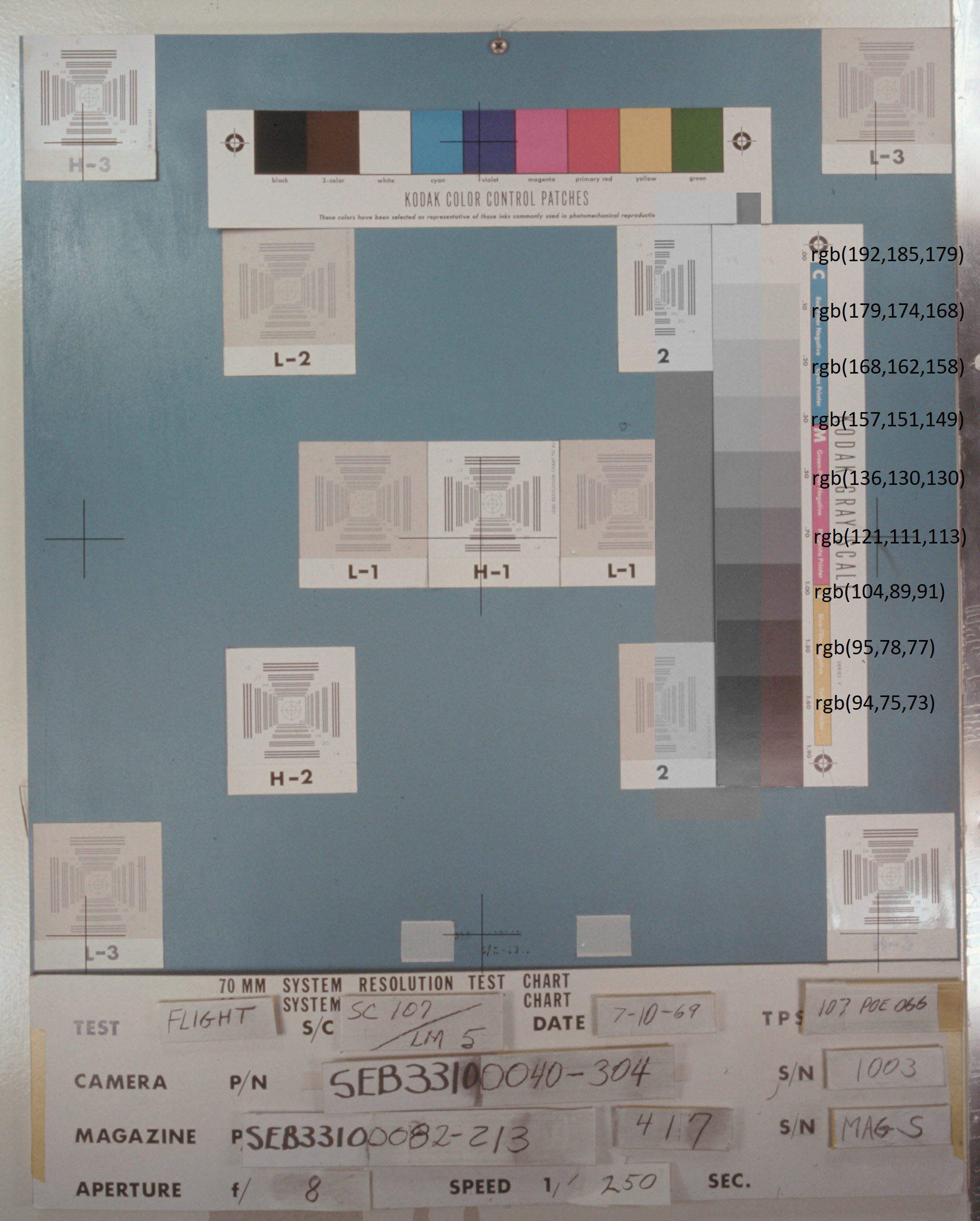
La película no está "desaparecida" en el color "azul", sino en el "rojo". E incluso después de eso, por alguna razón, la superficie lunar en la fotografía de la NASA es gris.

El resultado de colorear la foto AS11-37-5455 :



Esta es una de las raras fotografías del programa Apollo, donde la superficie lunar tiene un tinte marrón, aunque no del todo. A los opositores de la teoría de la conspiración lunar les encanta mostrarlo, dicen, miren, el marrón es el mismo. Pero aquí entró la trampa. Analicemos la foto como gráfico 11-37 , que muestra la imagen correspondiente de gradaciones grises:



La película simplemente "se volvió" marrón. Esa es la razón del tinte marrón de la superficie lunar en las fotografías de la NASA.

La dependencia del color de la superficie lunar de las condiciones de iluminación y observación.

Utilizando los datos LRO presentados en [ 9 ] , estudiamos cómo cambia el color de la superficie lunar debido a las condiciones de iluminación y observación. Considere la fuente de luz E490 (el Sol desde el espacio) y los diferentes valores de los ángulos i , e , $$$\ varPsi$ . La siguiente imagen muestra el resultado, donde los colores en la fila superior son tres veces más brillantes y los colores en la fila inferior se reducen al mismo brillo Y = 0.5 .



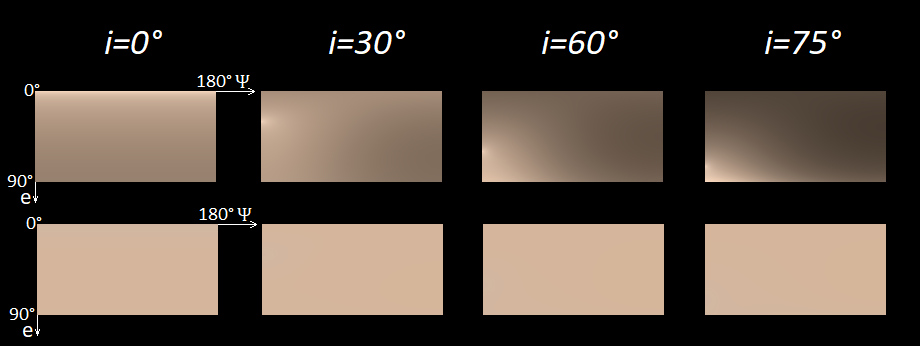
Como puede ver en la imagen, solo cambia el brillo. En la fila inferior, los colores son casi los mismos en todas partes para el ojo humano. Aunque, si observa de cerca, en el caso i = 0 °, puede ver una desviación muy débil hacia el lado gris cuando e se acerca a cero.

El color del suelo lunar.

Hay una fotografía muy extraña en el sitio web de la NASA, a saber, esta fotografía de la muestra de suelo lunar No. 10005 .



El suelo lunar en la fotografía se ve marrón, incluso demasiado marrón, dado que la iluminación fue producida por una fuente de luz blanca. El balance de blancos correcto puede verificarse por el color del papel blanco que cayó en el marco.

¿Quizás es el mismo suelo anaranjado que descubrieron los astronautas del Apolo 17? No! El documento [ 11 ] establecía claramente que la muestra fue tomada por los astronautas del Apolo 11.

Ahora escuchemos lo que dice Neil Armstrong (astronauta del Apolo 11) en una entrevista con Patrick Moore [ 12 ] , que dio en 1970.

Cuando miras el suelo cerca o en tu mano, descubres que en realidad es gris carbón, y especialmente no pudimos encontrar nada diferente a este color.

(Cuando miras el material a corta distancia, como si estuvieras en tu mano, descubres que es de hecho un gris carbón, y nunca pudimos encontrar algo que fuera muy diferente de ese color).

Resulta que, Neil Armstrong, no tengo miedo de la palabra, mintió.

Literatura

1) Laboratorio de investigación de color y visión: nuevas funciones CIE XYZ transformadas de las funciones LIE de CIE (2006)
2) International Color Consortium: un espacio de color predeterminado estándar para Internet: sRGB
3) Recomendación UIT-RBT.709 - Valores de parámetros para los estándares de HDTV para producción e intercambio internacional de programas
4) Robertson R. "Cálculo de la temperatura de color correlacionada y la temperatura de distribución" /.Opt. Soc. Am. 58, 1528 (1968).
5) Referencia de espectro extraterrestre estándar ASTM 2000 E-490-00
6) CIE Standard Illuminant D65
7) "Los primeros resultados de la determinación de las propiedades fisico-mecánicas de los suelos de la luna", Moscú: 1970. Gosstroy, URSS, bajo la dirección de prof. Dr. tech. Ciencias de V. G. Bulychev, p. 8.
8) Shevchenko V.V., Moon y su observación, 1983, pp. 91-92.
9) Hapke, B., B. Denevi, H. Sato, S. Braden y M. Robinson (2012), La dependencia de la longitud de onda de la curva de fase lunar vista por la Cámara Gran Angular del Orbitador de Reconocimiento Lunar, J. Geophys. Res., 117, E00H15
10) Ohtake, M. et al. (2010), Derivando la reflectancia absoluta de la superficie lunar utilizando datos de imágenes multibanda SELENE (Kaguya), Space Sci. Rev., 154, 57-77
11) APOLLO 11 TUBOS DE CONDUCCIÓN, Disección y descripción por Judith H. Allton, NASA (1978)
12) BBC Neil Armstrong Entrevista con Patrick Moore (1970)