Nota Traducción abreviada, más bien volver a contar en sus propias palabras.
UPD: como se señaló en los comentarios, los ejemplos no son perfectos. El autor no está buscando la mejor solución al problema, su objetivo es explicar la complejidad de los algoritmos "en los dedos".Se necesita una notación O grande para describir la complejidad de los algoritmos. Para esto, se utiliza el concepto de tiempo. El tema es aterrador para muchos, los programadores evitan hablar sobre "el tiempo del orden N" es algo común.
Si puede evaluar el código en términos de Big O, lo más probable es que se lo considere un "tipo inteligente". Y lo más probable es que pases por tu próxima entrevista. No se detendrá con la pregunta de si es posible reducir la complejidad de cualquier código para n log n contra n ^ 2.
Estructuras de datos
La elección de la estructura de datos depende de la tarea específica: del tipo de datos y del algoritmo para su procesamiento. Se creó una variedad de estructuras de datos (en .NET o Java o Elixir) para ciertos tipos de algoritmos.
A menudo, al elegir una u otra estructura, simplemente copiamos la solución generalmente aceptada. En la mayoría de los casos, esto es suficiente. Pero, de hecho, sin comprender la complejidad de los algoritmos, no podemos hacer una elección informada. El tema de las estructuras de datos solo se puede pasar después de la complejidad de los algoritmos.
Aquí usaremos solo matrices de números (como en una entrevista). Ejemplos de JavaScript.
Comencemos con el más simple: O (1)
Tome una matriz de 5 números:
const nums = [1,2,3,4,5];
Suponga que necesita obtener el primer elemento. Usamos el índice para esto:
const nums = [1,2,3,4,5]; const firstNumber = nums[0];
¿Qué tan complicado es este algoritmo? Podemos decir: "nada complicado, simplemente tome el primer elemento de la matriz". Esto es cierto, pero es más correcto describir la complejidad a través del número de operaciones realizadas para lograr el resultado, dependiendo de la entrada (
operaciones de entrada).
En otras palabras: cuántas operaciones aumentarán a medida que aumente el número de parámetros de entrada.
En nuestro ejemplo, hay 5 parámetros de entrada, porque hay 5 elementos en la matriz. Para obtener el resultado, debe realizar una operación (tomar un elemento por índice). ¿Cuántas operaciones serán necesarias si hay 100 elementos en la matriz? O 1000? O 100.000? De todos modos, solo se necesita una operación.
Es decir: "una operación para todos los datos de entrada posibles" - O (1).
O (1) puede leerse como "complejidad de orden 1" (orden 1) o "algoritmo se ejecuta en tiempo constante / constante" (tiempo constante).
Ya has adivinado que los algoritmos O (1) son los más eficientes.
Iteraciones y "tiempo de orden n": O (n)
Ahora busquemos la suma de los elementos de la matriz:
const nums = [1,2,3,4,5]; let sum = 0; for(let num of nums){ sum += num; }
Nuevamente nos preguntamos: ¿cuántas operaciones de entrada necesitamos? Aquí debe ordenar todos los elementos, es decir operación en cada elemento. Cuanto más grande es la matriz, más operaciones.
Uso de la notación Big O: O (n), o "complejidad del orden n (orden n)". Además, este tipo de algoritmo se llama "lineal" o que el algoritmo está "escalado linealmente".
Análisis
¿Podemos hacer la suma más eficiente? En general no. ¿Y si sabemos que la matriz está garantizada para comenzar en 1, ordenada y no tiene huecos? Entonces podemos aplicar la fórmula S = n (n + 1) / 2 (donde n es el último elemento de la matriz):
const sumContiguousArray = function(ary){
Tal algoritmo es mucho más eficiente que O (n), además, se ejecuta en "tiempo constante / constante", es decir es O (1).
De hecho, hay más de una operación: necesita obtener la longitud de la matriz, obtener el último elemento, realizar la multiplicación y la división. ¿No es eso O (3) o algo así? En la notación Big O, el número real de pasos no es importante, es importante que el algoritmo se ejecute en tiempo constante.
Los algoritmos de tiempo constante son siempre O (1). Lo mismo con los algoritmos lineales, de hecho, las operaciones pueden ser O (n + 5), en Big O la notación es O (n).
No son las mejores soluciones: O (n ^ 2)
Escribamos una función que verifique la matriz en busca de duplicados. Solución de bucle anidado:
const hasDuplicates = function (num) {
Ya sabemos que la iteración de matriz es O (n). Tenemos un bucle anidado, para cada elemento que iteramos nuevamente, es decir O (n ^ 2) o "complejidad del orden n cuadrado".
Los algoritmos con bucles anidados sobre la misma colección son siempre O (n ^ 2).
"La complejidad del orden de log n": O (log n)
En el ejemplo anterior, un bucle anidado, por sí solo (si no tiene en cuenta que está anidado), tiene complejidad O (n), porque Es la enumeración de los elementos de la matriz. Este ciclo termina tan pronto como se encuentra el elemento deseado, es decir de hecho, no todos los elementos serán enumerados. Pero la notación Big O siempre considera el peor de los casos: el elemento que está buscando puede ser el último.
Aquí, un bucle anidado se usa para buscar un elemento dado en una matriz. La búsqueda de un elemento en una matriz, bajo ciertas condiciones, se puede optimizar, hacerlo mejor que O lineal (n).
Deje que se ordene la matriz. Luego podemos usar el algoritmo de búsqueda binaria: dividir la matriz en dos mitades, descartar lo innecesario, dividir el resto nuevamente en dos partes, y así sucesivamente hasta encontrar el valor deseado. Este tipo de algoritmo se llama divide y vencerás Divide y vencerás.
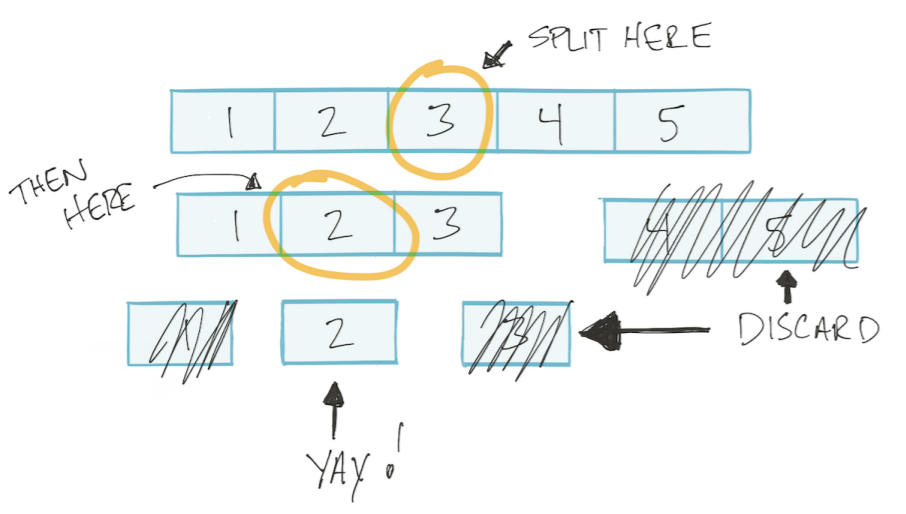
Este algoritmo se basa en un logaritmo.
Descripción rápida de los logaritmos
Considere un ejemplo, ¿a qué será igual x?
x ^ 3 = 8
Necesitamos tomar la raíz cúbica de 8, esto será 2. Ahora más difícil
2 ^ x = 512
Usando el logaritmo, el problema se puede escribir como
log2 (512) = x
"El logaritmo de base 2 de 512 es x". Presta atención a la "base 2", es decir pensamos en dos: cuántas veces necesitas multiplicar 2 para obtener 512.
En el algoritmo de búsqueda binaria, en cada paso dividimos la matriz en dos partes.
Mi adicion. Es decir en el peor de los casos, realizamos tantas operaciones como podemos dividir la matriz en dos partes. Por ejemplo, ¿cuántas veces podemos dividir una matriz de 4 elementos en dos partes? 2 veces ¿Y una matriz de 8 elementos? 3 veces Es decir número de divisiones / operaciones = log2 (n) (donde n es el número de elementos en la matriz).
Resulta que la dependencia del número de operaciones en el número de elementos de entrada se describe como log2 (n)
Por lo tanto, utilizando la notación Big O, el algoritmo de búsqueda binaria tiene complejidad O (log n).
Mejore O (n ^ 2) a O (n log n)
Volvamos a la tarea de verificar la matriz en busca de duplicados. Realizamos iteraciones sobre todos los elementos de la matriz, y para cada elemento nuevamente iteramos. Hicieron O (n) dentro de O (n), es decir O (n * n) u O (n ^ 2).
Podemos reemplazar el bucle anidado con una búsqueda binaria *. Es decir solo tenemos que pasar por todos los elementos de O (n), dentro hacemos O (log n). Resulta O (n * log n) u O (n log n).
const nums = [1, 2, 3, 4, 5]; const searchFor = function (items, num) {
* ATENCIÓN, para evitar la
impresión . Usar la búsqueda binaria para verificar una matriz en busca de duplicados es una mala solución. Solo muestra cómo, en términos de Big O, evaluar la complejidad del algoritmo que se muestra en la lista de códigos anterior. Un buen algoritmo o uno malo no es importante para este artículo; la visibilidad es importante.
Pensando en términos de Big O
- Obtener el elemento de colección es O (1). Si se obtiene por índice en una matriz o por clave en un diccionario en notación Big O, será O (1)
- Iterando sobre una colección es O (n)
- Los bucles anidados sobre la misma colección son O (n ^ 2)
- Divide y vencerás siempre O (log n)
- Las iteraciones que usan Divide and Conquer son O (n log n)