En los artículos anteriores, discutimos el motor de indexación PostgreSQL, la interfaz de los métodos de acceso y dos métodos de acceso: índice hash y árbol B. En este artículo, describiremos los índices GiST.

Gist

GiST es una abreviatura de "árbol de búsqueda generalizada". Este es un árbol de búsqueda equilibrado, al igual que "b-tree" discutido anteriormente.

Cual es la diferencia El índice "Btree" está estrictamente conectado a la semántica de comparación: todo lo que es capaz de hacer es el soporte de operadores "mayores", "menores" e "iguales" (¡pero muy capaces!) Sin embargo, las bases de datos modernas almacenan tipos de datos para los cuales estos operadores simplemente no tiene sentido: geodatos, documentos de texto, imágenes, ...

El método de índice GiST nos ayuda en estos tipos de datos. Permite definir una regla para distribuir datos de un tipo arbitrario en un árbol equilibrado y un método para utilizar esta representación para el acceso de algún operador. Por ejemplo, el índice GiST puede "acomodar" el árbol R para datos espaciales con soporte de operadores de posición relativa (ubicados a la izquierda, a la derecha, contiene, etc.) o el árbol RD para conjuntos con soporte de operadores de intersección o inclusión.

Gracias a la extensibilidad, se puede crear un método totalmente nuevo desde cero en PostgreSQL: para este fin, se debe implementar una interfaz con el motor de indexación. Pero esto requiere una premeditación no solo de la lógica de indexación, sino también de la asignación de estructuras de datos a páginas, la implementación eficiente de bloqueos y el soporte de un registro de escritura anticipada. Todo esto supone altas habilidades de desarrollo y un gran esfuerzo humano. GiST simplifica la tarea al hacerse cargo de los problemas de bajo nivel y ofrecer su propia interfaz: varias funciones que no pertenecen a las técnicas, sino al dominio de la aplicación. En este sentido, podemos considerar GiST como un marco para construir nuevos métodos de acceso.

Estructura

GiST es un árbol de altura equilibrada que consta de páginas de nodos. Los nodos consisten en filas de índice.

Cada fila de un nodo hoja (fila hoja), en general, contiene algún predicado (expresión booleana) y una referencia a una fila de tabla (TID). Los datos indexados (clave) deben cumplir con este predicado.

Cada fila de un nodo interno (fila interna) también contiene un predicado y una referencia a un nodo secundario, y todos los datos indexados del subárbol secundario deben cumplir con este predicado. En otras palabras, el predicado de una fila interna incluye los predicados de todas las filas secundarias. Este rasgo importante del índice GiST reemplaza la simple ordenación del árbol B.

La búsqueda en el árbol GiST utiliza una función de coherencia especializada ("coherente"), una de las funciones definidas por la interfaz e implementada a su manera para cada familia de operadores admitida.

Se llama a la función de coherencia para una fila de índice y determina si el predicado de esta fila es coherente con el predicado de búsqueda (especificado como " expresión de operador de campo indexado "). Para una fila interna, esta función realmente determina si es necesario descender al subárbol correspondiente, y para una fila de hoja, la función determina si los datos indexados cumplen con el predicado.

La búsqueda comienza con un nodo raíz, como una búsqueda de árbol normal. La función de coherencia permite averiguar en qué nodos secundarios tiene sentido ingresar (puede haber varios) y cuáles no. El algoritmo se repite para cada nodo secundario encontrado. Y si el nodo es hoja, la fila seleccionada por la función de coherencia se devuelve como uno de los resultados.

La búsqueda es profunda primero: el algoritmo primero intenta alcanzar un nodo hoja. Esto permite devolver los primeros resultados pronto siempre que sea posible (lo que podría ser importante si el usuario está interesado en solo varios resultados en lugar de en todos).

Observemos una vez más que la función de coherencia no necesita tener nada que ver con operadores "mayores", "menores" o "iguales". La semántica de la función de consistencia puede ser bastante diferente y, por lo tanto, no se supone que el índice devuelva valores en un cierto orden.

No discutiremos los algoritmos de inserción y eliminación de valores en GiST: algunas funciones de interfaz más realizan estas operaciones. Sin embargo, hay un punto importante. Cuando se inserta un nuevo valor en el índice, la posición para este valor en el árbol se selecciona de modo que los predicados de sus filas principales se extiendan lo menos posible (idealmente, no se extienden en absoluto). Pero cuando se elimina un valor, el predicado de la fila principal ya no se reduce. Esto solo sucede en casos como estos: una página se divide en dos (cuando la página no tiene suficiente espacio para la inserción de una nueva fila de índice) o el índice se recrea desde cero (con el comando REINDEX o VACUUM FULL). Por lo tanto, la eficiencia del índice GiST para los datos que cambian con frecuencia puede degradarse con el tiempo.

Además, consideraremos algunos ejemplos de índices para varios tipos de datos y propiedades útiles de GiST:

• Puntos (y otras entidades geométricas) y búsqueda de vecinos más cercanos.
• Intervalos y restricciones de exclusión.
• Búsqueda de texto completo.

R-tree para puntos

Ilustraremos lo anterior con un ejemplo de un índice para puntos en un plano (también podemos construir índices similares para otras entidades geométricas). Un árbol B normal no se adapta a este tipo de datos ya que no se definen operadores de comparación para los puntos.

La idea de R-tree es dividir el plano en rectángulos que en total cubran todos los puntos que se indexan. Una fila de índice almacena un rectángulo, y el predicado se puede definir así: "el punto buscado se encuentra dentro del rectángulo dado".

La raíz del árbol R contendrá varios rectángulos más grandes (posiblemente intersectados). Los nodos secundarios contendrán rectángulos de menor tamaño que están incrustados en el primario y en total cubren todos los puntos subyacentes.

En teoría, los nodos hoja deben contener puntos que se indexan, pero el tipo de datos debe ser el mismo en todas las filas de índice y, por lo tanto, nuevamente los rectángulos se almacenan, pero se "colapsan" en puntos.

Para visualizar dicha estructura, proporcionamos imágenes para tres niveles del árbol R. Los puntos son coordenadas de aeropuertos (similares a los de la tabla "aeropuertos" de la base de datos de demostración , pero se proporcionan más datos de openflights.org ).


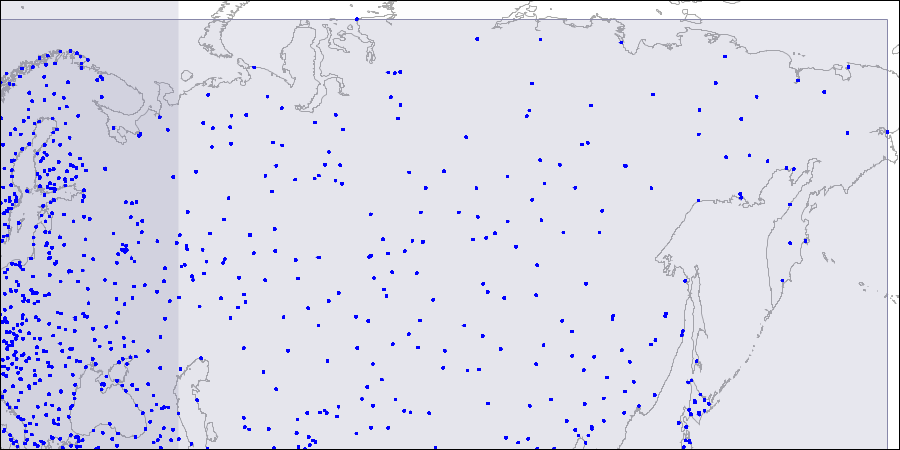Nivel uno: dos grandes rectángulos que se cruzan son visibles.


Nivel dos: los rectángulos grandes se dividen en áreas más pequeñas.


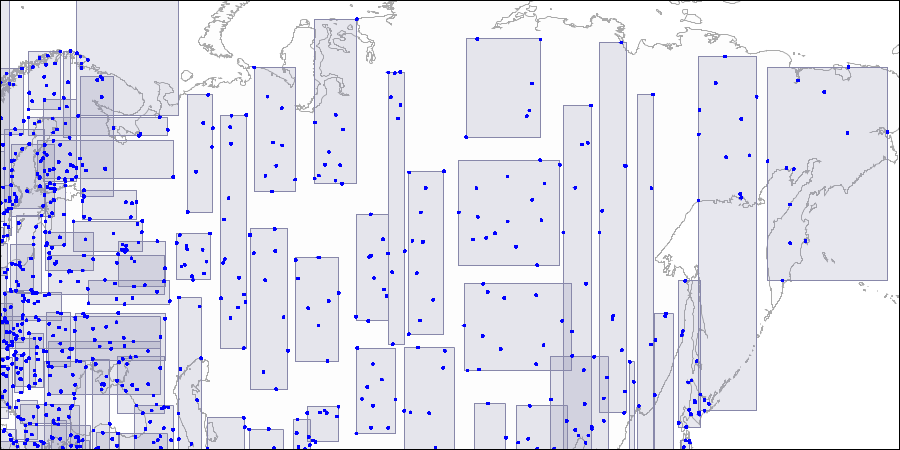Nivel tres: cada rectángulo contiene tantos puntos como para caber en una página de índice.

Ahora consideremos un ejemplo muy simple de "un nivel":

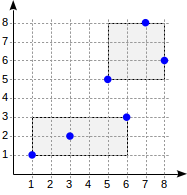
postgres=# create table points(p point); postgres=# insert into points(p) values (point '(1,1)'), (point '(3,2)'), (point '(6,3)'), (point '(5,5)'), (point '(7,8)'), (point '(8,6)'); postgres=# create index on points using gist(p); 

Con esta división, la estructura del índice tendrá el siguiente aspecto:



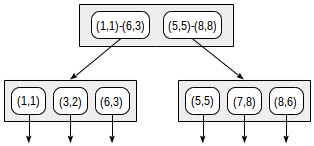
El índice creado se puede usar para acelerar la siguiente consulta, por ejemplo: "buscar todos los puntos contenidos en el rectángulo dado". Esta condición se puede formalizar de la siguiente manera: p <@ box '(2,1),(6,3)' (operador <@ de la familia "points_ops" significa "contenido en"):

 postgres=# set enable_seqscan = off; postgres=# explain(costs off) select * from points where p <@ box '(2,1),(7,4)'; 

  QUERY PLAN ---------------------------------------------- Index Only Scan using points_p_idx on points Index Cond: (p <@ '(7,4),(2,1)'::box) (2 rows) 

La función de coherencia del operador (" campo indexado <@ expresión ", donde el campo indexado es un punto y la expresión es un rectángulo) se define de la siguiente manera. Para una fila interna, devuelve "sí" si su rectángulo se cruza con el rectángulo definido por la expresión . Para una fila de hojas, la función devuelve "sí" si su punto (rectángulo "colapsado") está contenido en el rectángulo definido por la expresión.



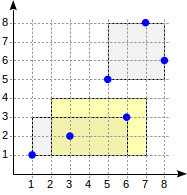
La búsqueda comienza con el nodo raíz. El rectángulo (2,1) - (7,4) se cruza con (1,1) - (6,3), pero no se cruza con (5,5) - (8,8), por lo tanto, no es necesario para descender al segundo subárbol.



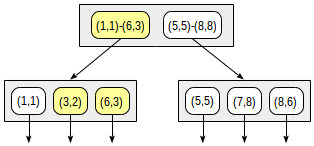
Al llegar a un nodo hoja, pasamos por los tres puntos contenidos allí y devolvemos dos de ellos como resultado: (3.2) y (6.3).

 postgres=# select * from points where p <@ box '(2,1),(7,4)'; 

  p ------- (3,2) (6,3) (2 rows) 

Internos

Desafortunadamente, la "inspección de página" habitual no permite buscar en el índice GiST. Pero hay otra forma disponible: extensión "gevel". No se incluye en la entrega estándar, por lo tanto, consulte las instrucciones de instalación .

Si todo se hace correctamente, tres funciones estarán disponibles para usted. Primero, podemos obtener algunas estadísticas:

 postgres=# select * from gist_stat('airports_coordinates_idx'); 

  gist_stat ------------------------------------------ Number of levels: 4 + Number of pages: 690 + Number of leaf pages: 625 + Number of tuples: 7873 + Number of invalid tuples: 0 + Number of leaf tuples: 7184 + Total size of tuples: 354692 bytes + Total size of leaf tuples: 323596 bytes + Total size of index: 5652480 bytes+ (1 row) 

Está claro que el tamaño del índice en las coordenadas del aeropuerto es de 690 páginas y que el índice consta de cuatro niveles: la raíz y dos niveles internos se muestran en las figuras anteriores, y el cuarto nivel es hoja.

En realidad, el índice de ocho mil puntos será significativamente más pequeño: aquí se creó con un factor de relleno del 10% para mayor claridad.

En segundo lugar, podemos generar el árbol de índice:

 postgres=# select * from gist_tree('airports_coordinates_idx'); 

  gist_tree ----------------------------------------------------------------------------------------- 0(l:0) blk: 0 numTuple: 5 free: 7928b(2.84%) rightlink:4294967295 (InvalidBlockNumber) + 1(l:1) blk: 335 numTuple: 15 free: 7488b(8.24%) rightlink:220 (OK) + 1(l:2) blk: 128 numTuple: 9 free: 7752b(5.00%) rightlink:49 (OK) + 1(l:3) blk: 57 numTuple: 12 free: 7620b(6.62%) rightlink:35 (OK) + 2(l:3) blk: 62 numTuple: 9 free: 7752b(5.00%) rightlink:57 (OK) + 3(l:3) blk: 72 numTuple: 7 free: 7840b(3.92%) rightlink:23 (OK) + 4(l:3) blk: 115 numTuple: 17 free: 7400b(9.31%) rightlink:33 (OK) + ... 

Y tercero, podemos generar los datos almacenados en filas de índice. Tenga en cuenta el siguiente matiz: el resultado de la función debe convertirse al tipo de datos necesario. En nuestra situación, este tipo es "caja" (un rectángulo delimitador). Por ejemplo, observe cinco filas en el nivel superior:

 postgres=# select level, a from gist_print('airports_coordinates_idx') as t(level int, valid bool, a box) where level = 1; 

  level | a -------+----------------------------------------------------------------------- 1 | (47.663586,80.803207),(-39.2938003540039,-90) 1 | (179.951004028,15.6700000762939),(15.2428998947144,-77.9634017944336) 1 | (177.740997314453,73.5178070068359),(15.0664,10.57970047) 1 | (-77.3191986083984,79.9946975708),(-179.876998901,-43.810001373291) 1 | (-39.864200592041,82.5177993774),(-81.254096984863,-64.2382965088) (5 rows) 

En realidad, las cifras proporcionadas anteriormente se crearon solo a partir de estos datos.

Operadores para buscar y ordenar

Los operadores discutidos hasta ahora (como <@ en el predicado p <@ box '(2,1),(7,4)' ) pueden llamarse operadores de búsqueda ya que especifican condiciones de búsqueda en una consulta.

También hay otro tipo de operador: operadores de pedidos. Se utilizan para especificaciones del orden de clasificación en la cláusula ORDER BY en lugar de especificaciones convencionales de nombres de columna. El siguiente es un ejemplo de dicha consulta:

 postgres=# select * from points order by p <-> point '(4,7)' limit 2; 

  p ------- (5,5) (7,8) (2 rows) 

p <-> point '(4,7)' aquí es una expresión que usa un operador de orden <-> , que denota la distancia de un argumento al otro. El significado de la consulta es devolver dos puntos más cercanos al punto (4.7). Una búsqueda como esta se conoce como k-NN - k-búsqueda de vecinos más cercanos.

Para admitir consultas de este tipo, un método de acceso debe definir una función de distancia adicional, y el operador de pedido debe incluirse en la clase de operador apropiada (por ejemplo, clase "points_ops" para puntos). La consulta a continuación muestra los operadores, junto con sus tipos ("s" - buscar y "o" - ordenar):

 postgres=# select amop.amopopr::regoperator, amop.amoppurpose, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'point_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'gist' and amop.amoplefttype = opc.opcintype; 

  amopopr | amoppurpose | amopstrategy -------------------+-------------+-------------- <<(point,point) | s | 1 strictly left >>(point,point) | s | 5 strictly right ~=(point,point) | s | 6 coincides <^(point,point) | s | 10 strictly below >^(point,point) | s | 11 strictly above <->(point,point) | o | 15 distance <@(point,box) | s | 28 contained in rectangle <@(point,polygon) | s | 48 contained in polygon <@(point,circle) | s | 68 contained in circle (9 rows) 

También se muestran los números de estrategias, con sus significados explicados. Está claro que hay muchas más estrategias que para "btree", solo algunas de ellas son compatibles con puntos. Se pueden definir diferentes estrategias para otros tipos de datos.

La función de distancia se llama para un elemento de índice y debe calcular la distancia (teniendo en cuenta la semántica del operador) desde el valor definido por la expresión (" expresión de operador de ordenación de campo indexado ") hasta el elemento dado. Para un elemento hoja, esta es solo la distancia al valor indexado. Para un elemento interno, la función debe devolver el mínimo de las distancias a los elementos secundarios de la hoja. Dado que recorrer todas las filas secundarias sería bastante costoso, se permite que la función subestime de manera optimista la distancia, pero a expensas de reducir la eficiencia de búsqueda. Sin embargo, la función nunca puede sobreestimar la distancia, ya que esto interrumpirá el trabajo del índice.

La función de distancia puede devolver valores de cualquier tipo ordenable (para ordenar valores, PostgreSQL usará semántica de comparación de la familia de operadores apropiada del método de acceso "btree", como se describió anteriormente ).

Para los puntos en un plano, la distancia se interpreta en un sentido muy habitual: el valor de (x1,y1) <-> (x2,y2) es igual a la raíz cuadrada de la suma de los cuadrados de las diferencias de las abscisas y las ordenadas. La distancia desde un punto a un rectángulo delimitador se considera la distancia mínima desde el punto a este rectángulo o cero si el punto se encuentra dentro del rectángulo. Es fácil calcular este valor sin caminar a través de puntos secundarios, y el valor no es mayor que la distancia a cualquier punto secundario.

Consideremos el algoritmo de búsqueda para la consulta anterior.



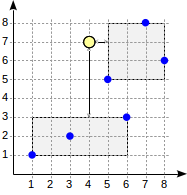
La búsqueda comienza con el nodo raíz. El nodo contiene dos rectángulos delimitadores. La distancia a (1,1) - (6,3) es 4.0 y a (5,5) - (8,8) es 1.0.

Los nodos secundarios se recorren en el orden de aumentar la distancia. De esta manera, primero descendemos al nodo hijo más cercano y calculamos las distancias a los puntos (mostraremos los números en la figura para visibilidad):



Esta información es suficiente para devolver los dos primeros puntos, (5,5) y (7,8). Como somos conscientes de que la distancia a los puntos que se encuentran dentro del rectángulo (1,1) - (6,3) es 4.0 o mayor, no necesitamos descender al primer nodo secundario.

Pero, ¿y si necesitáramos encontrar los primeros tres puntos?

 postgres=# select * from points order by p <-> point '(4,7)' limit 3; 

  p ------- (5,5) (7,8) (8,6) (3 rows) 

Aunque el segundo nodo secundario contiene todos estos puntos, no podemos devolver (8,6) sin mirar el primer nodo secundario ya que este nodo puede contener puntos más cercanos (desde 4.0 <4.1).



Para las filas internas, este ejemplo aclara los requisitos para la función de distancia. Al seleccionar una distancia más pequeña (4.0 en lugar de 4.5 real) para la segunda fila, redujimos la eficiencia (el algoritmo comenzó a examinar innecesariamente un nodo adicional), pero no rompió la corrección del algoritmo.

Hasta hace poco, GiST era el único método de acceso capaz de tratar con operadores de pedidos. Pero la situación ha cambiado: el método de acceso RUM (que se discutirá más adelante) ya se ha unido a este grupo de métodos, y no es improbable que el viejo árbol B se una a ellos: se está implementando un parche desarrollado por Nikita Glukhov, nuestro colega. discutido por la comunidad.

A partir de marzo de 2019, se agregó compatibilidad con k-NN para SP-GiST en el próximo PostgreSQL 12 (también creado por Nikita). El parche para B-tree todavía está en progreso.

R-árbol para intervalos

Otro ejemplo del uso del método de acceso GiST es la indexación de intervalos, por ejemplo, intervalos de tiempo (tipo "tsrange"). La diferencia es que los nodos internos contendrán intervalos delimitadores en lugar de rectángulos delimitadores.

Consideremos un ejemplo simple. Alquilaremos una cabaña y almacenaremos los intervalos de reserva en una tabla:

 postgres=# create table reservations(during tsrange); postgres=# insert into reservations(during) values ('[2016-12-30, 2017-01-09)'), ('[2017-02-23, 2017-02-27)'), ('[2017-04-29, 2017-05-02)'); postgres=# create index on reservations using gist(during); 

El índice se puede utilizar para acelerar la siguiente consulta, por ejemplo:

 postgres=# select * from reservations where during && '[2017-01-01, 2017-04-01)'; 

  during ----------------------------------------------- ["2016-12-30 00:00:00","2017-01-08 00:00:00") ["2017-02-23 00:00:00","2017-02-26 00:00:00") (2 rows) 

 postgres=# explain (costs off) select * from reservations where during && '[2017-01-01, 2017-04-01)'; 

  QUERY PLAN ------------------------------------------------------------------------------------ Index Only Scan using reservations_during_idx on reservations Index Cond: (during && '["2017-01-01 00:00:00","2017-04-01 00:00:00")'::tsrange) (2 rows) 

&& operador && para intervalos denota intersección; por lo tanto, la consulta debe devolver todos los intervalos que se cruzan con el dado. Para dicho operador, la función de coherencia determina si el intervalo dado se cruza con un valor en una fila interna o de hoja.

Tenga en cuenta que esto no se trata de obtener intervalos en un cierto orden, aunque los operadores de comparación se definen para intervalos. Podemos usar el índice "btree" para intervalos, pero en este caso, tendremos que prescindir de operaciones como estas:

 postgres=# select amop.amopopr::regoperator, amop.amoppurpose, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'range_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'gist' and amop.amoplefttype = opc.opcintype; 

  amopopr | amoppurpose | amopstrategy -------------------------+-------------+-------------- @>(anyrange,anyelement) | s | 16 contains element <<(anyrange,anyrange) | s | 1 strictly left &<(anyrange,anyrange) | s | 2 not beyond right boundary &&(anyrange,anyrange) | s | 3 intersects &>(anyrange,anyrange) | s | 4 not beyond left boundary >>(anyrange,anyrange) | s | 5 strictly right -|-(anyrange,anyrange) | s | 6 adjacent @>(anyrange,anyrange) | s | 7 contains interval <@(anyrange,anyrange) | s | 8 contained in interval =(anyrange,anyrange) | s | 18 equals (10 rows) 

(Excepto la igualdad, que está contenida en la clase de operador para el método de acceso "btree").

Internos

Podemos mirar dentro usando la misma extensión "gevel". Solo necesitamos recordar cambiar el tipo de datos en la llamada a gist_print:

 postgres=# select level, a from gist_print('reservations_during_idx') as t(level int, valid bool, a tsrange); 

  level | a -------+----------------------------------------------- 1 | ["2016-12-30 00:00:00","2017-01-09 00:00:00") 1 | ["2017-02-23 00:00:00","2017-02-27 00:00:00") 1 | ["2017-04-29 00:00:00","2017-05-02 00:00:00") (3 rows) 

Restricción de exclusión

El índice GiST se puede usar para admitir restricciones de exclusión (EXCLUDE).

La restricción de exclusión asegura que los campos dados de cualquiera de las dos filas de la tabla no se "correspondan" entre sí en términos de algunos operadores. Si se elige el operador "igual", obtenemos exactamente la restricción única: los campos dados de dos filas no son iguales entre sí.

La restricción de exclusión es compatible con el índice, así como la restricción única. Podemos elegir cualquier operador para que:

1. Es compatible con el método de índice: propiedad "can_exclude" (por ejemplo, "btree", GiST o SP-GiST, pero no GIN).
2. Es conmutativo, es decir, se cumple la condición: un operador b = b operador a.

Esta es una lista de estrategias adecuadas y ejemplos de operadores (los operadores, como recordamos, pueden tener diferentes nombres y estar disponibles no para todos los tipos de datos):

• Para "btree":
  
  • "Igual" =
• Para GiST y SP-GiST:
  
  • "Intersección" &&
  • "Coincidencia" ~=
  • Adyacencia -|-

Tenga en cuenta que podemos usar el operador de igualdad en una restricción de exclusión, pero no es práctico: una restricción única será más eficiente. Eso es exactamente por qué no tocamos las restricciones de exclusión cuando discutimos los árboles B.

Proporcionemos un ejemplo del uso de una restricción de exclusión. Es razonable no permitir reservas para intervalos de intersección.

 postgres=# alter table reservations add exclude using gist(during with &&); 

Una vez que creamos la restricción de exclusión, podemos agregar filas:

 postgres=# insert into reservations(during) values ('[2017-06-10, 2017-06-13)'); 

Pero un intento de insertar un intervalo de intersección en la tabla dará como resultado un error:

 postgres=# insert into reservations(during) values ('[2017-05-15, 2017-06-15)'); 

 ERROR: conflicting key value violates exclusion constraint "reservations_during_excl" DETAIL: Key (during)=(["2017-05-15 00:00:00","2017-06-15 00:00:00")) conflicts with existing key (during)=(["2017-06-10 00:00:00","2017-06-13 00:00:00")). 

Extensión "Btree_gist"

Vamos a complicar el problema. Ampliamos nuestro humilde negocio, y vamos a alquilar varias casas de campo:

 postgres=# alter table reservations add house_no integer default 1; 

Necesitamos cambiar la restricción de exclusión para que se tengan en cuenta los números de las casas. Sin embargo, GiST no admite la operación de igualdad para números enteros:

 postgres=# alter table reservations drop constraint reservations_during_excl; postgres=# alter table reservations add exclude using gist(during with &&, house_no with =); 

 ERROR: data type integer has no default operator class for access method "gist" HINT: You must specify an operator class for the index or define a default operator class for the data type. 

En este caso, la extensión " btree_gist " ayudará, lo que agrega el soporte GiST de las operaciones inherentes a los B-trees. GiST, eventualmente, puede soportar cualquier operador, entonces ¿por qué no deberíamos enseñarlo a soportar operadores "mayores", "menores" e "iguales"?

 postgres=# create extension btree_gist; postgres=# alter table reservations add exclude using gist(during with &&, house_no with =); 

Ahora todavía no podemos reservar la primera cabaña para las mismas fechas:

 postgres=# insert into reservations(during, house_no) values ('[2017-05-15, 2017-06-15)', 1); 

 ERROR: conflicting key value violates exclusion constraint "reservations_during_house_no_excl" 

Sin embargo, podemos reservar el segundo:

 postgres=# insert into reservations(during, house_no) values ('[2017-05-15, 2017-06-15)', 2); 

Pero tenga en cuenta que aunque GiST de alguna manera puede admitir operadores "mayores", "menores" e "iguales", B-tree todavía lo hace mejor. Por lo tanto, vale la pena usar esta técnica solo si se necesita esencialmente el índice GiST, como en nuestro ejemplo.

RD-tree para búsqueda de texto completo

Acerca de la búsqueda de texto completo

Comencemos con una introducción minimalista a la búsqueda de texto completo de PostgreSQL (si está al tanto, puede omitir esta sección).

La tarea de la búsqueda de texto completo es seleccionar del conjunto de documentos aquellos documentos que coinciden con la consulta de búsqueda. (Si hay muchos documentos coincidentes, es importante encontrar la mejor coincidencia , pero no diremos nada al respecto en este momento).

Para fines de búsqueda, un documento se convierte en un tipo especializado "tsvector", que contiene lexemas y sus posiciones en el documento. Los lexemas son palabras convertidas a la forma adecuada para la búsqueda. Por ejemplo, las palabras generalmente se convierten en minúsculas y las terminaciones variables se cortan:

 postgres=# select to_tsvector('There was a crooked man, and he walked a crooked mile'); 

  to_tsvector ----------------------------------------- 'crook':4,10 'man':5 'mile':11 'walk':8 (1 row) 

También podemos ver que algunas palabras (llamadas palabras de detención ) se descartan por completo ("allí", "era", "a", "y", "él"), ya que presumiblemente ocurren con demasiada frecuencia para buscarlas para que tengan sentido. Todas estas conversiones ciertamente pueden configurarse, pero esa es otra historia.

Una consulta de búsqueda se representa con otro tipo: "tsquery". Aproximadamente, una consulta consta de uno o varios lexemas unidos por conectivos: "y" &, "o" |, "no"! .. También podemos usar paréntesis para aclarar la prioridad de la operación.

 postgres=# select to_tsquery('man & (walking | running)'); 

  to_tsquery ---------------------------- 'man' & ( 'walk' | 'run' ) (1 row) 

Solo se utiliza un operador de coincidencia @@ para la búsqueda de texto completo.

 postgres=# select to_tsvector('There was a crooked man, and he walked a crooked mile') @@ to_tsquery('man & (walking | running)'); 

  ?column? ---------- t (1 row) 

 postgres=# select to_tsvector('There was a crooked man, and he walked a crooked mile') @@ to_tsquery('man & (going | running)'); 

  ?column? ---------- f (1 row) 

Esta información es suficiente por ahora. Nos sumergiremos un poco más en la búsqueda de texto completo en el próximo artículo que presenta el índice GIN.

RD-árboles

Para una búsqueda rápida de texto completo, en primer lugar, la tabla debe almacenar una columna de tipo "tsvector" (para evitar realizar una conversión costosa cada vez que se busca) y, en segundo lugar, se debe construir un índice en esta columna. Uno de los posibles métodos de acceso para esto es GiST.

 postgres=# create table ts(doc text, doc_tsv tsvector); postgres=# create index on ts using gist(doc_tsv); postgres=# insert into ts(doc) values ('Can a sheet slitter slit sheets?'), ('How many sheets could a sheet slitter slit?'), ('I slit a sheet, a sheet I slit.'), ('Upon a slitted sheet I sit.'), ('Whoever slit the sheets is a good sheet slitter.'), ('I am a sheet slitter.'), ('I slit sheets.'), ('I am the sleekest sheet slitter that ever slit sheets.'), ('She slits the sheet she sits on.'); postgres=# update ts set doc_tsv = to_tsvector(doc); 

Sin duda, es conveniente confiar un disparador al último paso (conversión del documento a "tsvector").

 postgres=# select * from ts; 

 -[ RECORD 1 ]---------------------------------------------------- doc | Can a sheet slitter slit sheets? doc_tsv | 'sheet':3,6 'slit':5 'slitter':4 -[ RECORD 2 ]---------------------------------------------------- doc | How many sheets could a sheet slitter slit? doc_tsv | 'could':4 'mani':2 'sheet':3,6 'slit':8 'slitter':7 -[ RECORD 3 ]---------------------------------------------------- doc | I slit a sheet, a sheet I slit. doc_tsv | 'sheet':4,6 'slit':2,8 -[ RECORD 4 ]---------------------------------------------------- doc | Upon a slitted sheet I sit. doc_tsv | 'sheet':4 'sit':6 'slit':3 'upon':1 -[ RECORD 5 ]---------------------------------------------------- doc | Whoever slit the sheets is a good sheet slitter. doc_tsv | 'good':7 'sheet':4,8 'slit':2 'slitter':9 'whoever':1 -[ RECORD 6 ]---------------------------------------------------- doc | I am a sheet slitter. doc_tsv | 'sheet':4 'slitter':5 -[ RECORD 7 ]---------------------------------------------------- doc | I slit sheets. doc_tsv | 'sheet':3 'slit':2 -[ RECORD 8 ]---------------------------------------------------- doc | I am the sleekest sheet slitter that ever slit sheets. doc_tsv | 'ever':8 'sheet':5,10 'sleekest':4 'slit':9 'slitter':6 -[ RECORD 9 ]---------------------------------------------------- doc | She slits the sheet she sits on. doc_tsv | 'sheet':4 'sit':6 'slit':2 

¿Cómo debe estructurarse el índice? El uso de R-tree directamente no es una opción, ya que no está claro cómo definir un "rectángulo delimitador" para los documentos. Pero podemos aplicar alguna modificación de este enfoque para conjuntos, un llamado árbol RD (RD significa "Muñeca Rusa"). Se entiende que un conjunto es un conjunto de lexemas en este caso, pero en general, un conjunto puede ser cualquiera.

Una idea de los árboles RD es reemplazar un rectángulo delimitador con un conjunto delimitador, es decir, un conjunto que contenga todos los elementos de los conjuntos secundarios.

Surge una pregunta importante sobre cómo representar conjuntos en filas de índice. La forma más directa es enumerar todos los elementos del conjunto. Esto podría verse de la siguiente manera:



Entonces, por ejemplo, para el acceso por condición doc_tsv @@ to_tsquery('sit') podríamos descender solo a los nodos que contienen el lexema "sit":



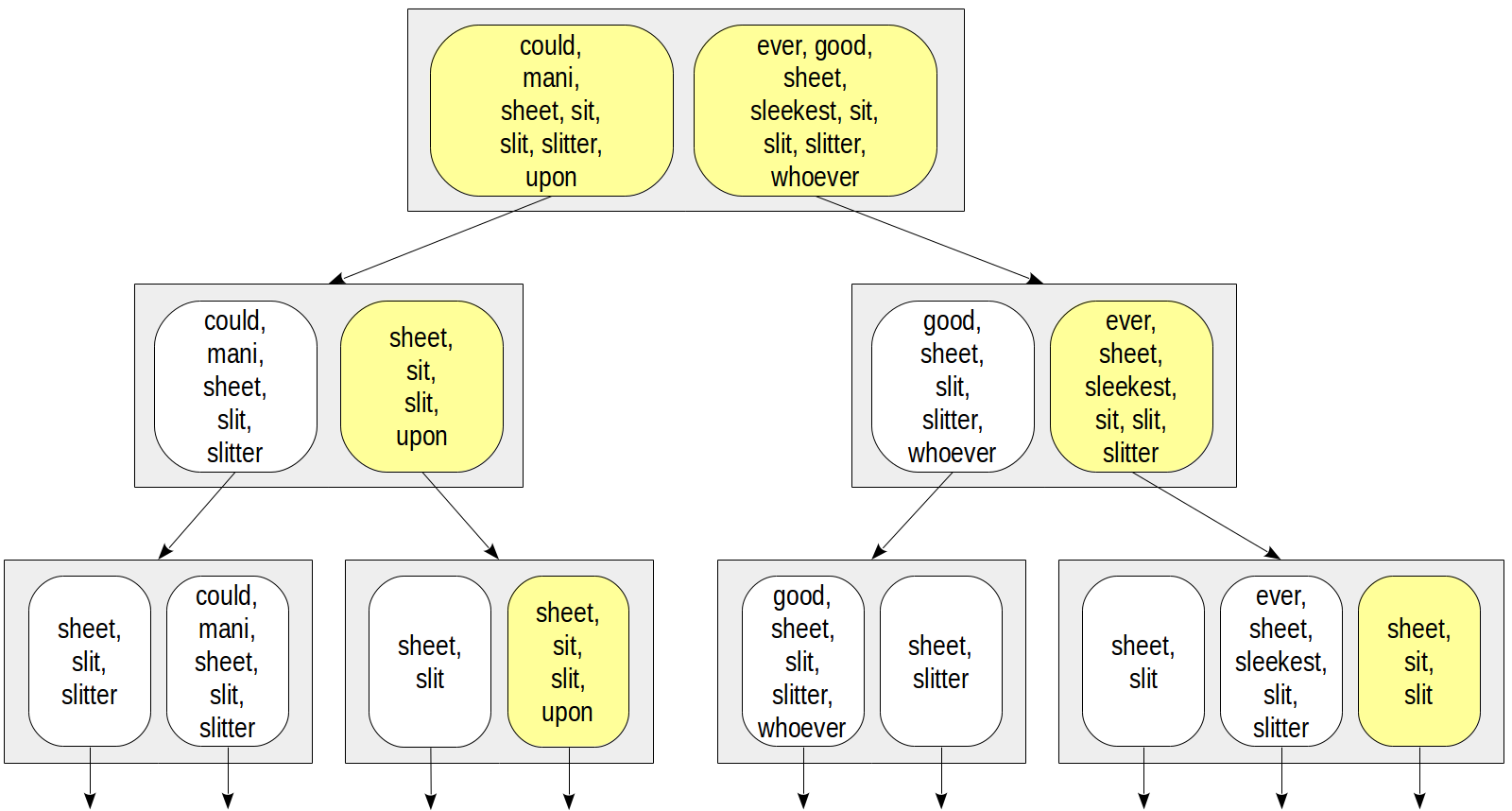
Esta representación tiene problemas evidentes. El número de lexemas en un documento puede ser bastante grande, por lo que las filas de índice tendrán un gran tamaño y entrarán en TOAST, lo que hará que el índice sea mucho menos eficiente. Incluso si cada documento tiene pocos lexemas únicos, la unión de conjuntos puede ser muy grande: cuanto mayor sea la raíz, mayores serán las filas de índice.

A veces se usa una representación como esta, pero para otros tipos de datos. Y la búsqueda de texto completo utiliza otra solución más compacta: el denominado árbol de firmas . Su idea es bastante familiar para todos los que trataron con el filtro Bloom.

Cada lexema se puede representar con su firma : una cadena de bits de cierta longitud donde todos los bits menos uno son cero. La posición de este bit está determinada por el valor de la función hash del lexema (discutimos los aspectos internos de las funciones hash anteriormente ).

La firma del documento es el OR bit a bit de las firmas de todos los lexemas del documento.

Asumamos las siguientes firmas de lexemas:

 podría 1,000,000
 siempre 0001000
 bien 0000010
 mani 0000100
 hoja 0000100
 0100000 más elegante
 sentarse 0010000
 hendidura 0001000
 cortadora 0000001
 sobre 0000010
 quien sea 0010000

Entonces las firmas de los documentos son así:

 ¿Puede una cortadora de hojas cortar hojas?  0001101
 ¿Cuántas hojas podría cortar una cortadora de hojas?  1001101
 Corté una hoja, una hoja que corté.  0001100
 Sobre una sábana cortada me siento.  0011110
 Quien cortó las sábanas es una buena cortadora de sábanas.  0011111
 Soy una cortadora de sábanas.  0000101
 Corté sábanas.  0001100
 Soy la cortadora de sábanas más elegante que jamás haya cortado las sábanas.  0101101
 Ella corta la sábana en la que se sienta.  0011100

El árbol de índice se puede representar de la siguiente manera:



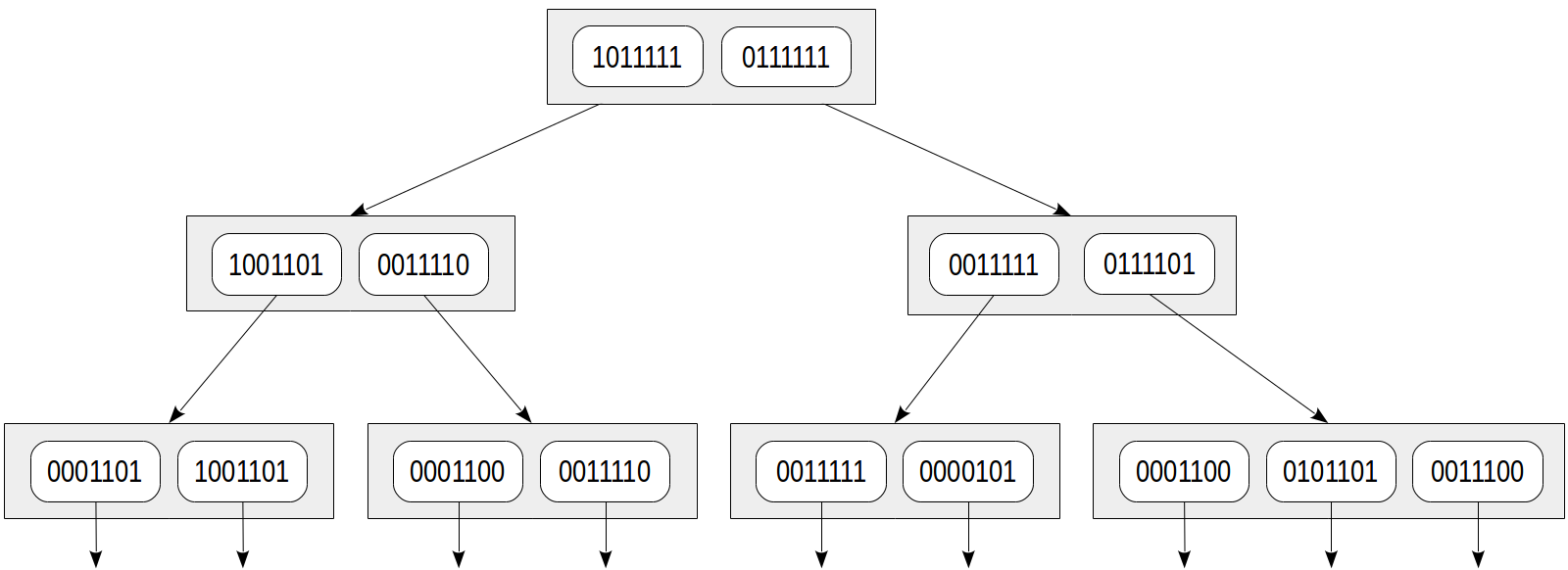
Las ventajas de este enfoque son evidentes: las filas de índice tienen tamaños pequeños iguales, y dicho índice es compacto. Pero un inconveniente también es claro: la precisión se sacrifica a la compacidad.

Consideremos la misma condición doc_tsv @@ to_tsquery('sit') . Y calculemos la firma de la consulta de búsqueda de la misma manera que para el documento: 0010000 en este caso. La función de coherencia debe devolver todos los nodos secundarios cuyas firmas contienen al menos un bit de la firma de consulta:



Compare con la figura anterior: podemos ver que el árbol se volvió amarillo, lo que significa que se producen falsos positivos y se pasan nodos excesivos durante la búsqueda. Aquí recogimos el lexema "quienquiera", cuya firma desafortunadamente era la misma que la firma del lexema "sentarse". Es importante que no se puedan producir falsos negativos en el patrón, es decir, estamos seguros de no perder los valores necesarios.

Además, puede suceder que diferentes documentos también obtengan las mismas firmas: en nuestro ejemplo, los documentos desafortunados son "He cortado una hoja, he cortado una hoja" y "He cortado hojas" (ambos tienen la firma de 0001100). Y si una fila de índice de hoja no almacena el valor de "tsvector", el índice mismo dará falsos positivos. Por supuesto, en este caso, el método le pedirá al motor de indexación que vuelva a verificar el resultado con la tabla, para que el usuario no vea estos falsos positivos. Pero la eficiencia de la búsqueda puede verse comprometida.

En realidad, una firma es de 124 bytes en la implementación actual en lugar de 7 bits en las figuras, por lo que es mucho menos probable que ocurran los problemas anteriores que en el ejemplo. Pero en realidad, también se indexan muchos más documentos. Para reducir de alguna manera el número de falsos positivos del método de índice, la implementación se vuelve un poco complicada: el "tsvector" indexado se almacena en una fila de índice de hoja, pero solo si su tamaño no es grande (un poco menos de 1/16 de una página, que es aproximadamente medio kilobyte para páginas de 8 KB).

Ejemplo

Para ver cómo funciona la indexación en los datos reales, tomemos el archivo del correo electrónico "pgsql-hackers". La versión utilizada en el ejemplo contiene 356125 mensajes con la fecha de envío, asunto, autor y texto:

 fts=# select * from mail_messages order by sent limit 1; 

 -[ RECORD 1 ]------------------------------------------------------------------------ id | 1572389 parent_id | 1562808 sent | 1997-06-24 11:31:09 subject | Re: [HACKERS] Array bug is still there.... author | "Thomas G. Lockhart" <Thomas.Lockhart@jpl.nasa.gov> body_plain | Andrew Martin wrote: + | > Just run the regression tests on 6.1 and as I suspected the array bug + | > is still there. The regression test passes because the expected output+ | > has been fixed to the *wrong* output. + | + | OK, I think I understand the current array behavior, which is apparently+ | different than the behavior for v1.0x. + ... 

Agregar y completar la columna de tipo "tsvector" y construir el índice. Aquí uniremos tres valores en un vector (asunto, autor y texto del mensaje) para mostrar que el documento no necesita ser un solo campo, sino que puede constar de partes arbitrarias totalmente diferentes.

 fts=# alter table mail_messages add column tsv tsvector; fts=# update mail_messages set tsv = to_tsvector(subject||' '||author||' '||body_plain); 

 NOTICE: word is too long to be indexed DETAIL: Words longer than 2047 characters are ignored. ... UPDATE 356125 

 fts=# create index on mail_messages using gist(tsv); 

Como podemos ver, un cierto número de palabras se descartaron debido al tamaño demasiado grande. Pero el índice finalmente se crea y puede admitir consultas de búsqueda:

 fts=# explain (analyze, costs off) select * from mail_messages where tsv @@ to_tsquery('magic & value'); 

  QUERY PLAN ---------------------------------------------------------- Index Scan using mail_messages_tsv_idx on mail_messages (actual time=0.998..416.335 rows=898 loops=1) Index Cond: (tsv @@ to_tsquery('magic & value'::text)) Rows Removed by Index Recheck: 7859 Planning time: 0.203 ms Execution time: 416.492 ms (5 rows) 

Podemos ver que junto con 898 filas que coinciden con la condición, el método de acceso devolvió 7859 filas más que se filtraron al volver a verificar con la tabla. Esto demuestra un impacto negativo de la pérdida de precisión en la eficiencia.

Internos

Para analizar el contenido del índice, usaremos nuevamente la extensión "gevel":

 fts=# select level, a from gist_print('mail_messages_tsv_idx') as t(level int, valid bool, a gtsvector) where a is not null; 

  level | a -------+------------------------------- 1 | 992 true bits, 0 false bits 2 | 988 true bits, 4 false bits 3 | 573 true bits, 419 false bits 4 | 65 unique words 4 | 107 unique words 4 | 64 unique words 4 | 42 unique words ... 

Los valores del tipo especializado "gtsvector" que se almacenan en filas de índice son en realidad la firma más, tal vez, la fuente "tsvector". Si el vector está disponible, la salida contiene el número de lexemas (palabras únicas), de lo contrario, el número de bits verdaderos y falsos en la firma.

Está claro que en el nodo raíz, la firma degeneró en "todos", es decir, un nivel de índice se volvió absolutamente inútil (y uno más se volvió casi inútil, con solo cuatro bits falsos).

Propiedades

Veamos las propiedades del método de acceso GiST (las consultas se proporcionaron anteriormente ):

  amname | name | pg_indexam_has_property --------+---------------+------------------------- gist | can_order | f gist | can_unique | f gist | can_multi_col | t gist | can_exclude | t 

La ordenación de valores y la restricción única no son compatibles. Como hemos visto, el índice puede construirse en varias columnas y usarse en restricciones de exclusión.

Las siguientes propiedades de capa de índice están disponibles:

  name | pg_index_has_property ---------------+----------------------- clusterable | t index_scan | t bitmap_scan | t backward_scan | f 

Y las propiedades más interesantes son las de la capa de columna. Algunas de las propiedades son independientes de las clases de operador:

  name | pg_index_column_has_property --------------------+------------------------------ asc | f desc | f nulls_first | f nulls_last | f orderable | f search_array | f search_nulls | t 

(La ordenación no es compatible; el índice no se puede utilizar para buscar una matriz; se admiten NULL).

Pero las dos propiedades restantes, "distancia_orderable" y "retornable", dependerán de la clase de operador utilizada. Por ejemplo, para los puntos obtendremos:

  name | pg_index_column_has_property --------------------+------------------------------ distance_orderable | t returnable | t 

La primera propiedad indica que el operador de distancia está disponible para buscar vecinos más cercanos. Y el segundo dice que el índice puede usarse para escaneo de solo índice. Aunque las filas de índice de hoja almacenan rectángulos en lugar de puntos, el método de acceso puede devolver lo que se necesita.

Las siguientes son las propiedades de los intervalos:

  name | pg_index_column_has_property --------------------+------------------------------ distance_orderable | f returnable | t 

Para intervalos, la función de distancia no está definida y, por lo tanto, no es posible buscar vecinos más cercanos.

Y para la búsqueda de texto completo, obtenemos:

  name | pg_index_column_has_property --------------------+------------------------------ distance_orderable | f returnable | f 

Se ha perdido la compatibilidad con el escaneo de solo índice ya que las filas de la hoja pueden contener solo la firma sin los datos en sí. Sin embargo, esta es una pérdida menor ya que a nadie le interesa el valor del tipo "tsvector" de todos modos: este valor se utiliza para seleccionar filas, mientras que es el texto fuente que debe mostrarse, pero de todos modos falta en el índice.

Otros tipos de datos

Finalmente, mencionaremos algunos tipos más que actualmente son compatibles con el método de acceso GiST, además de los tipos geométricos ya discutidos (por ejemplo, puntos), intervalos y tipos de búsqueda de texto completo.

De los tipos estándar, este es el tipo " inet " para las direcciones IP. Todo lo demás se agrega a través de extensiones:

• cube proporciona el tipo de datos "cube" para cubos multidimensionales. Para este tipo, al igual que para los tipos geométricos en un plano, se define la clase de operador GiST: R-tree, que admite la búsqueda de vecinos más cercanos.
  
• seg proporciona el tipo de datos "seg" para intervalos con límites especificados con cierta precisión y agrega compatibilidad con el índice GiST para este tipo de datos (R-tree).
  
• intarray amplía la funcionalidad de las matrices de enteros y agrega compatibilidad con GiST para ellas. Se implementan dos clases de operador: "gist__int_ops" (árbol RD con una representación completa de las claves en las filas de índice) y "gist__bigint_ops" (árbol RD de firma). La primera clase se puede utilizar para matrices pequeñas y la segunda, para tamaños más grandes.
  
• ltree agrega el tipo de datos "ltree" para estructuras en forma de árbol y el soporte GiST para este tipo de datos (árbol RD).
  
• pg_trgm agrega una clase de operador especializada "gist_trgm_ops" para el uso de trigramas en la búsqueda de texto completo. Pero esto se discutirá más a fondo, junto con el índice GIN.
  

Sigue leyendo .