Recuerdo una conclusión importante de las partes anteriores. Para un comportamiento secuencial cíclico que no contiene múltiples señales (cambio de un ciclo más de dos veces), la función lógica mínima de cada señal se puede representar de la siguiente forma (naturalmente, en ausencia de conflictos CSC):
1)
donde a * b * ... * c es el implicante de una o más variables. g + h + ... + i: este es posiblemente un conjunto vacío de implicantes que consta de una variable. x * f es un implante de 2 variables, cuya presencia en forma mínima no es necesaria. Todas las variables, excepto x, se pueden incluir en la fórmula tanto en forma directa como inversa, dependiendo de la disposición de los signos de los eventos correspondientes. Todas las variables se incluyen en la fórmula como argumentos estrictamente una vez.
Antes de continuar, veremos más de cerca un fenómeno como la descomposición. En primer lugar, la descomposición es de interés, lo que preserva la auto-sincronización. Al descomponer una función lógica NOT-AND-OR, se puede distinguir como un nuevo elemento:
a) uno o más implicados,
b) varias señales (variables) de un implante,
c) un inversor de entrada.
Para empezar, consideramos un caso especial de la función NOR AND. El comportamiento de dicha función lógica (x = a + b + c + d) para el modelo en cuestión:
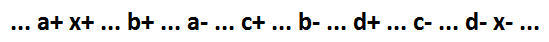
Ella puede distinguir varias señales como un elemento separado.
De hecho, la selección de un nuevo elemento durante la descomposición es la adición de una nueva señal (f). Para mantener el comportamiento correcto, la semi-modularidad y la auto-sincronización, el cambio de la señal recién agregada f debe tener eventos de consecuencia. Dado que la descomposición afecta solo a un elemento del circuito (en este caso, x) y no afecta a los elementos restantes del circuito, el cambio de la señal f solo puede causar el cambio de la señal x. De lo contrario, la función lógica de otra señal dependería de la señal f. Dada esta conclusión, intentemos resaltar varias variables, excepto la variable a como un nuevo elemento f. Tomemos por ejemplo las variables by c. Forman el elemento lógico f = b + c.
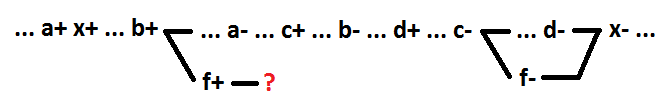
Como se puede ver, para el evento f + es imposible determinar el evento consecuencia sin violar la corrección del comportamiento. Cualquier grupo de señales que no contenga la variable a no puede asignarse como un elemento separado mientras se mantiene la auto-sincronización.
Una señal como la de este ejemplo se llamará encendido. En el caso general, la señal de conmutación para la función OR (AND) es una señal cuyo cambio a 1 (0) cambia el valor de la función de 0 a 1 (de 1 a 0). Para mantener la auto-sincronización durante la descomposición de la función lógica OR (Y) al seleccionar un nuevo elemento, debe usar la señal de conmutación. Al seleccionar un nuevo elemento, también es necesario usar solo las señales que forman una cadena conectada (en el ejemplo a continuación a + b). x = f + c + d, f = a + b.
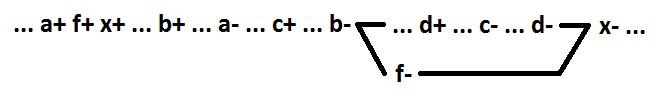
Cuando se usan señales a + b + d, la auto-sincronización no se conserva.
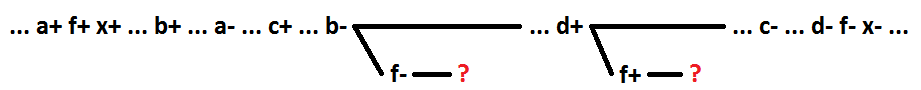
Por lo tanto, para comportamientos secuenciales sin señales múltiples durante la descomposición de la función lógica OR (I), destacando como el nuevo elemento los primeros en el curso del despliegue del proceso de señal, comenzando por el de conmutación, garantiza la auto-sincronización del circuito.
Ahora considere la función no OR (x =! A +! B). Como elemento separado (f) mientras se mantiene la sincronización automática, solo se puede seleccionar el inversor de entrada que corresponde a la señal de conmutación (x = f +! B, f =! A). La separación de otros inversores de entrada como un elemento separado conducirá a una violación de la auto-sincronización.
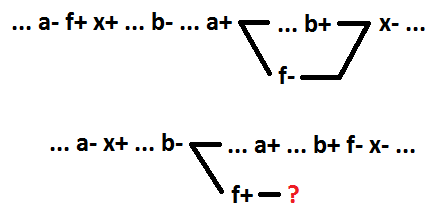
Pasemos a la función AND-OR. De manera similar, como señal de conmutación para la función OR, definimos el implicante de conmutación para la función AND-OR. Esto es un implicante, cambiar el valor del cual de 0 a 1 conduce a un cambio en el valor de la función de 0 a 1. Del mismo modo, como se descubrió para la función OR, para comportamientos secuenciales sin señales múltiples al descomponer la función AND-OR lógica, seleccionando los primeros como un elemento nuevo. En el proceso de despliegue, el implicante, comenzando con la inclusión, garantiza la preservación de la auto-sincronización del circuito. De lo contrario, la auto-sincronización se romperá. En el ejemplo a continuación, antes de la descomposición x = a * b + c. Después de la descomposición, x = f + c, f = a * b.
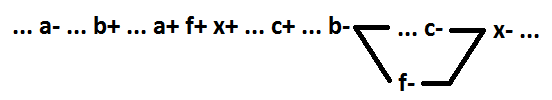
Ahora para la función AND-OR, consideramos la selección como un nuevo elemento de varias variables incluidas en el mismo implicante. Solo se consideran las funciones mínimas. A continuación se presentan todas las opciones posibles para el ejemplo de la función x = a * b * c + d (para la opción 4 - x = a * b * c + d + e, para la opción 6 - x = a * b * c * d + e) . El elemento resaltado es f = a * b.

En la opción 1, el cambio de una de las señales asignadas (a +) es la causa del evento x +. En la opción 2, la conmutación de una de las señales asignadas (a-) es la causa del evento x. En las opciones 3 y 4, la conmutación de una de las señales asignadas (a + y a-, respectivamente) se ubica entre los eventos x + yx-, y no es la causa del evento x-. La opción 5 es un caso especial de la opción 4, cuando el implicante, en el que se asignan las señales, es inclusivo. La opción restante 6: todas las conmutaciones de las señales asignadas se encuentran entre los eventos x- yx +, y no son las causas del evento x +.
Como puede ver, en las opciones 1 y 6, el evento f no se puede colocar correctamente. Dichas transformaciones no son descomposición con la preservación de la auto-sincronización. En las opciones 2, 3 y 4, se mantiene la auto-sincronización. Pero el valor de la función x resulta ser diferente de f * c + d (f * c + d + e para 4 opciones). Para 2 opciones - x = f * (d + c), para 3 opciones x = c * x + d *! F + x *! F, para 4 opciones x = (f + d) * (e + c). Tales transformaciones no son descomposiciones.
La única opción 5 es una descomposición con preservación de la auto-sincronización (x = f * c + d). En este caso, como un elemento separado en el implicante de inclusión, se seleccionan las primeras señales, comenzando con la inclusión (la señal que incluye el implicante de Y es la misma que la señal que incluye la función de AND). Pero, como se muestra arriba, se logra un resultado similar en dos pasos. Primero, se destaca la inclusión del implante. En el segundo paso, las primeras señales se seleccionan en el nuevo elemento, comenzando con la señal de conmutación.
Pasemos a la función NO-Y-O. Señalemos el inversor de entrada como un elemento separado. La señal a corresponde a la entrada del elemento x, al que está conectado un inversor de entrada dedicado (f =! A).
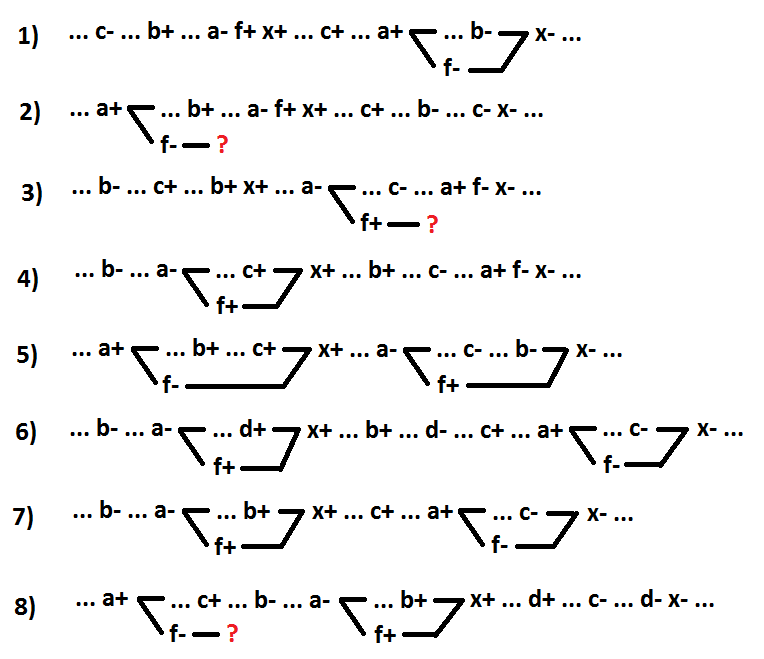
Opciones 1 y 2: la señal de conmutación a es la causa del evento x + (1 - x =! A + b * c, 2 - x = b *! A + c). Opciones 3 y 4: cambiar la señal a es la causa del evento x- (3 - x =! A + b * c, 4 - x =! A * b + c). Opciones 5 y 6: el cambio de la señal a se encuentra entre los eventos x + y x-, y no es la causa del evento x- (5 - x = b *! A + c, 6 - x =! A * b + d + c). La opción 7 es un caso especial de la opción 6, cuando la señal a es una señal de conmutación que incluye implicantes (x =! A * b + c). La opción restante 8: todas las señales de conmutación a se ubican entre los eventos x- yx +, y no son las causas del evento x + (x = c *! A * b + d).
Como puede ver, las opciones 2, 3 y 8 no son una descomposición con preservación de la auto-sincronización, ya que es imposible posicionar correctamente la señal de conmutación f. Para la opción 4, después de la conversión x = f * (c + b). Para la opción 5, después de la conversión x = c *! F +! F * x + b * x. Para la opción 6, después de la conversión x = (f + c) * (d + b). Estas transformaciones (opciones 4, 5 y 6) no son descomposiciones. Para la opción 7, después de la conversión x = f * b + c. La opción 7 es una descomposición con preservación de la auto-sincronización. En este caso, un inversor correspondiente a la señal de conmutación que incluye los implantes se asigna como un elemento separado. Se logra un resultado similar en dos pasos utilizando las transformaciones anteriores. Primero, se resalta la inclusión del implicante, luego se le asigna el inversor de entrada de la señal de encendido. Para la opción 1, después de la conversión x = f + b * c. La opción 1 también es una descomposición con preservación de la auto-sincronización. Este es un caso especial de la opción 7, cuando la inclusión del implicante consiste en una señal.
Sistematizamos los resultados obtenidos. Para el modelo en consideración, cuando se descompone una función lógica NO-Y-O para mantener el auto-sincronismo, solo son posibles las siguientes transformaciones: la asignación como un elemento separado:
1 - uno o más, comenzando desde el implicante superpuesto inclusivo (un caso especial - para la función de selección NO-OR de varias señales superpuestas, comenzando desde el inclusivo);
2 - en la inclusión implicante de varias, a partir de la inclusión, señales superpuestas;
3 - inversor de entrada correspondiente a la señal de conmutación incluyendo implicantes (un caso especial para la función NON-OR es la selección del inversor de entrada correspondiente a la señal de conmutación).
Estas transformaciones no permiten que el implicante sea inclusivo si no fue antes de la transformación. De ahí la conclusión: si una función lógica contiene un implicante, que consiste en más de una señal y no es inclusiva, dicha función no puede fragmentarse utilizando una descomposición que conserve la auto-sincronización, hasta elementos de dos entradas. Cualquier función lógica NOT-AND-OR en la que más de una variable contiene solo un implicante inclusivo se puede dividir en elementos de dos entradas (2AND-NOT, 2OR-NOT) utilizando una descomposición que preserva la auto-sincronización.
Paso 1: si el elemento lógico contiene solo un implicante (o todos los implicantes consisten en una variable), vaya al paso 3; de lo contrario, vaya al paso 2.
Paso 2: seleccione como elemento separado todos los implantes, excepto uno, comenzando con la inclusión. A continuación, trabajamos con el artículo recién recibido. Ve al paso 1.
Paso 3: si el elemento consta de dos variables, vaya al paso 5; de lo contrario, vaya al paso 4.
Paso 4: seleccionamos como elemento separado todas las variables, excepto una, comenzando con la inclusión. A continuación, trabajamos con el artículo recién recibido. Ve al paso 3.
Paso 5: se aplica a todos los elementos de dos entradas recibidos.
Paso 5.1: si los inversores de entrada están en ambas entradas, convertiremos el elemento a dual.
Paso 5.2: si el inversor de entrada es uno y corresponde a una señal que no se enciende, convertiremos el elemento en uno dual.
Paso 5.3: el inversor de entrada, si lo hay, se resalta como un elemento separado. Aplastamiento completado.
Ahora volvamos a la fórmula 1 al comienzo del texto. Si el implicante x * f no está en la expresión lógica, entonces la función se ve así: x = a * b * c + g + h + i. Su comportamiento:
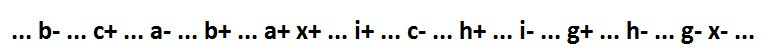
Como puede ver, el único implicante de más de una variable (a * b * c) es inclusivo. Y esta función con la ayuda de descomposición se puede fragmentar a los componentes mínimos mientras se mantiene la auto-sincronización.
Si el implicante x * f está presente en una expresión lógica, entonces la función se ve así: x = a * b * c + x * f + g + h + i. Su comportamiento:
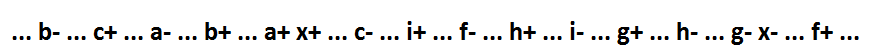
El implicante x * f no inclusivo consta de más de una variable. Dicha función no puede fragmentarse mientras se mantiene la auto-sincronización. Pero aplicamos una transformación que preserva la auto-sincronización: agregue la señal y - dual a la señal x. Agregar la señal y cambia la función de solo la señal xy la señal, cuyo cambio fue consecuencia del evento x- (la variable x se reemplaza por la variable y).
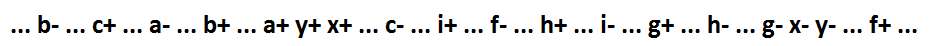
Ahora x = (f + i + h + g) * y, y = c * b * a + x. Los implicantes f + i + h + g y c * b * a que incluyen y, respectivamente, las funciones x e y pueden fragmentarse a los componentes mínimos mientras se mantiene la auto-sincronización.
Un modelo de comportamiento simplificado (sin paralelismo, elección y señales múltiples) le permite identificar propiedades que son naturalmente inherentes a los procesos binarios. La síntesis de circuitos sincrónicos en una base mínima es un fenómeno natural que no requiere ningún diseño.