En un artículo anterior, señalé qué tan extendido está el problema del mal uso del criterio t en las publicaciones científicas (y esto solo se puede hacer gracias a su apertura, y qué basura se crea cuando se usa en cualquier curso, informes, tareas de capacitación, etc., se desconoce) . Para discutir esto, hablé sobre los conceptos básicos del análisis de varianza y el nivel de significancia α establecido por el propio investigador. Pero para una comprensión completa de la imagen completa del análisis estadístico, es necesario enfatizar una serie de cosas importantes. Y el más básico de ellos es el concepto de error.
Error y aplicación incorrecta: ¿cuál es la diferencia?
Cualquier sistema físico contiene algún tipo de error, inexactitud. En la forma más diversa: la llamada tolerancia: la diferencia de tamaño de diferentes productos del mismo tipo; característica no lineal: cuando un dispositivo o método mide algo de acuerdo con una ley bien conocida dentro de ciertos límites, y luego se vuelve inaplicable; discreción: cuando técnicamente no podemos garantizar una característica de salida fluida.
Y al mismo tiempo, hay un error puramente humano: uso incorrecto de dispositivos, instrumentos, leyes matemáticas. Hay una diferencia fundamental entre el error inherente en el sistema y el error al aplicar este sistema. Es importante distinguir y no confundir entre sí estos dos conceptos, llamados la misma palabra "error". En este artículo, prefiero usar la palabra "error" para denotar las propiedades del sistema y "uso incorrecto", por su uso erróneo.
Es decir, el error de la regla es igual a la tolerancia del equipo, poniendo trazos en su lienzo. Un error en el sentido del uso incorrecto sería usarlo al medir los detalles de un reloj. El error del steelyard está escrito en él y asciende a unos 50 gramos, y el mal uso del steelyard sería pesar una bolsa de 25 kg, que estira el resorte desde la región de la ley de Hooke hasta la región de las deformaciones plásticas. El error de un microscopio de fuerza atómica se deriva de su discreción: no puede "tocar" objetos con una sonda más pequeña que con un diámetro de un átomo. Pero hay muchas formas de usarlo mal o de interpretar mal los datos. Y así sucesivamente.
Entonces, ¿qué tipo de error tiene esto en los métodos estadísticos? Y este error es precisamente el notorio nivel de significancia α.
Errores del primer y segundo tipo
Un error en el aparato matemático de la estadística es su esencia probabilística bayesiana misma. En el último artículo, ya mencioné en qué métodos estadísticos se basan: determinar el nivel de significancia α como la mayor probabilidad permitida para rechazar ilegalmente la hipótesis nula, y el investigador para asignar independientemente este valor al investigador.
¿Ya ves esta convención? De hecho, en los métodos de criterios no hay un rigor matemático familiar. Las matemáticas operan sobre características probabilísticas.
Y aquí llega otro punto donde es posible una mala interpretación de una palabra en un contexto diferente. Es necesario distinguir entre el concepto de probabilidad y la implementación real de un evento, expresado en la distribución de probabilidad. Por ejemplo, antes de comenzar cualquiera de nuestros experimentos, no sabemos qué tipo de valor obtendremos como resultado. Hay dos resultados posibles: habiendo hecho un cierto valor del resultado, realmente lo obtendremos o no. Es lógico que la probabilidad de ambos eventos sea 1/2. Pero la curva gaussiana que se muestra en el artículo anterior muestra
la distribución de probabilidad de que adivinemos correctamente la coincidencia.
Puede ilustrar esto claramente con un ejemplo. Permítanos tirar dos dados 600 veces: regular y trampa. Obtenemos los siguientes resultados:

Antes del experimento, para ambos cubos la pérdida de cualquier cara será igualmente probable: 1/6. Sin embargo, después del experimento, aparece la esencia del cubo de engaño, y podemos decir que la densidad de probabilidad de los seis que caen sobre él es del 90%.
Otro ejemplo que los químicos, físicos y cualquier persona interesada en los efectos cuánticos conocen son los orbitales atómicos. Teóricamente, un electrón puede ser "manchado" en el espacio y ubicado en casi cualquier lugar. Pero en la práctica hay áreas donde será en el 90 por ciento o más de los casos. Estas regiones del espacio formadas por una superficie con una densidad de probabilidad del electrón que es 90% son orbitales atómicos clásicos en forma de esferas, pesas, etc.
Entonces, al establecer independientemente el nivel de significancia, aceptamos deliberadamente el error descrito en su nombre. Debido a esto, ni un solo resultado puede considerarse "completamente confiable"; siempre nuestras conclusiones estadísticas contendrán alguna probabilidad de falla.
Un error formulado al determinar el nivel de significancia α se llama
error del primer tipo . Se puede definir como una "falsa alarma" o, más correctamente, un resultado falso positivo. De hecho, ¿qué significan las palabras "rechazar erróneamente la hipótesis nula"? Esto significa tomar por error los datos observados para detectar diferencias significativas entre los dos grupos. Hacer un diagnóstico falso sobre la presencia de la enfermedad, apresurarse a revelar al mundo un nuevo descubrimiento, que en realidad no existe: estos son ejemplos de errores de primer tipo.
Pero entonces, ¿debería haber resultados falsos negativos? Muy bien, y se llaman
errores del segundo tipo . Los ejemplos son un diagnóstico prematuro o una decepción como resultado del estudio, aunque de hecho contiene datos importantes. Los errores del segundo tipo están indicados por la letra, curiosamente, β. Pero este concepto en sí no es tan importante para las estadísticas como el número 1-β. El número 1-β se llama la
potencia del criterio , y como se puede adivinar, caracteriza la capacidad del criterio para no perderse un evento significativo.
Sin embargo, el contenido en los métodos estadísticos de errores del primer y segundo tipo no es solo su limitación. El concepto mismo de estos errores puede usarse directamente en el análisis estadístico. Como?
Análisis ROC
El análisis ROC (de la característica operativa del receptor) es un método para cuantificar la aplicabilidad de un determinado atributo a una clasificación binaria de objetos. En pocas palabras, podemos encontrar alguna forma de distinguir a las personas enfermas de las personas sanas, los gatos de los perros, los negros de los blancos, y luego verificar la validez de este método. Veamos un ejemplo nuevamente.
Permita que sea un científico forense en ciernes y desarrolle una nueva forma de determinar de manera discreta e inequívoca si una persona es un criminal. Se te ocurrió un signo cuantitativo: evaluar las inclinaciones criminales de las personas por la frecuencia con la que escuchan a Mikhail Krug. ¿Pero su síntoma dará resultados adecuados? Vamos a hacerlo bien.
Necesitará dos grupos de personas para validar sus criterios: ciudadanos comunes y delincuentes. De hecho, supongamos que el tiempo promedio anual que escuchan a Mikhail Krug difiere (vea la figura):
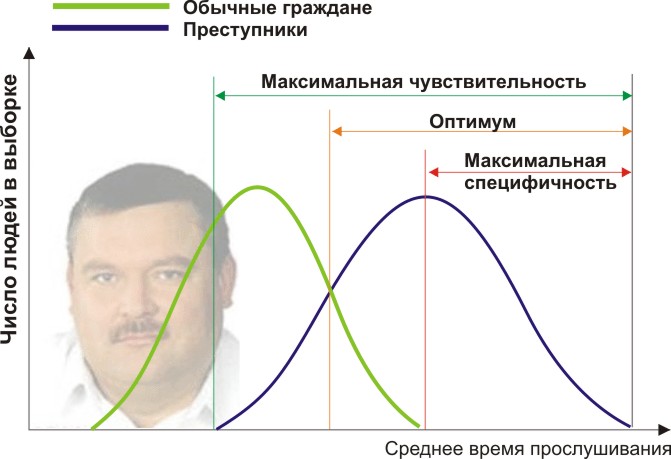
Aquí vemos que por el signo cuantitativo del tiempo de escucha, nuestras muestras se cruzan. Alguien escucha el Círculo espontáneamente en la radio sin cometer delitos, y alguien viola la ley al escuchar otra música o incluso ser sordo. ¿Qué condiciones de frontera tenemos? El análisis ROC introduce los conceptos de selectividad (sensibilidad) y especificidad. La sensibilidad se define como la capacidad de identificar todos los puntos de interés para nosotros (en este ejemplo, los delincuentes), y la especificidad, para no capturar nada falso positivo (para no sospechar a los habitantes comunes). Podemos establecer algunos rasgos cuantitativos críticos que separan algunos de los otros (naranja), que van desde la sensibilidad máxima (verde) hasta la especificidad máxima (rojo).
Veamos el siguiente diagrama:

Al cambiar el valor de nuestro atributo, cambiamos la proporción de resultados falsos positivos y falsos negativos (el área debajo de las curvas). Del mismo modo, podemos definir Sensibilidad = Posición. Res-t / (Positivo Res-t + falso negativo. Res-t) y Especificidad = Neg. Res-t / (Negativo Res-t + falso positivo. Res-t).
Pero lo más importante, podemos evaluar la proporción de positivos positivos a falsos positivos en todo el rango de valores de nuestro atributo cuantitativo, que es nuestra curva ROC deseada (ver figura):

¿Y cómo entendemos de este gráfico cuán bueno es nuestro atributo? Muy simple, calcule el área bajo la curva (AUC, área bajo la curva). La línea discontinua (0,0; 1,1) significa la coincidencia completa de las dos muestras y un criterio completamente sin sentido (el área bajo la curva es 0.5 del cuadrado completo). Pero la convexidad de la curva ROC solo indica la perfección del criterio. Si logramos encontrar un criterio tal que las muestras no se crucen en absoluto, entonces el área debajo de la curva ocupará todo el gráfico. En general, el rasgo se considera bueno, lo que permite separar de manera confiable una muestra de otra si AUC> 0.75-0.8.
Con este análisis, puede resolver una variedad de problemas. Habiendo decidido que muchas amas de casa estaban bajo sospecha debido a Michael Krug, y además, se echaron de menos los reincidentes peligrosos que escuchaban a Noggano, puede rechazar este criterio y desarrollar otro.
Después de haber surgido como una forma de procesar señales de radio e identificar "amigo o enemigo" después de un ataque a Pearl Harbor (de ahí el extraño nombre de las características del receptor), el análisis ROC se ha utilizado ampliamente en estadísticas biomédicas para analizar, validar, crear y caracterizar paneles de biomarcadores etc. Es flexible de usar si se basa en una lógica de sonido. Por ejemplo, puede desarrollar indicaciones para el examen médico de pacientes centrales retirados mediante la aplicación de un criterio altamente específico, aumentando la eficiencia de detección de enfermedades cardíacas y no sobrecargando a los médicos con pacientes innecesarios. Y durante una epidemia peligrosa de un virus previamente desconocido, por el contrario, se puede llegar a un criterio altamente selectivo para que nadie más se escape literalmente de la vacuna.
Nos encontramos con errores de ambos tipos y su visibilidad en la descripción de los criterios validados. Ahora, partiendo de estos fundamentos lógicos, podemos destruir una serie de descripciones estereotipadas falsas de los resultados. Algunas formulaciones incorrectas capturan nuestras mentes, a menudo confundidas por sus palabras y conceptos similares, y también por la poca atención que se presta a la interpretación incorrecta. Esto, tal vez, deberá escribirse por separado.