Algoritmo de triangulación de Delaunay por método de línea de barrido

Buen dia

En este artículo, describiré en detalle el algoritmo que obtuve como resultado de usar la idea de "barrer la línea recta" para construir la triangulación de Delaunay en un plano. Hay varias ideas que nunca conocí cuando leí artículos sobre triangulación.
Quizás alguien también los encuentre inusuales. Intentaré hacer todo con la mejor tradición e incluir lo siguiente en la historia: una descripción de las estructuras de datos utilizadas, una descripción de los pasos del algoritmo, prueba de corrección, estimaciones de tiempo, así como una comparación con un algoritmo iterativo que utiliza el árbol kD.

Definiciones y enunciado del problema.

Triangulación

Se dice que la triangulación se da en el conjunto de puntos en el plano si algunos pares de puntos están conectados por un borde, cualquier cara finita en el gráfico resultante forma un triángulo, los bordes no se cruzan y el gráfico es máximo en el número de bordes.

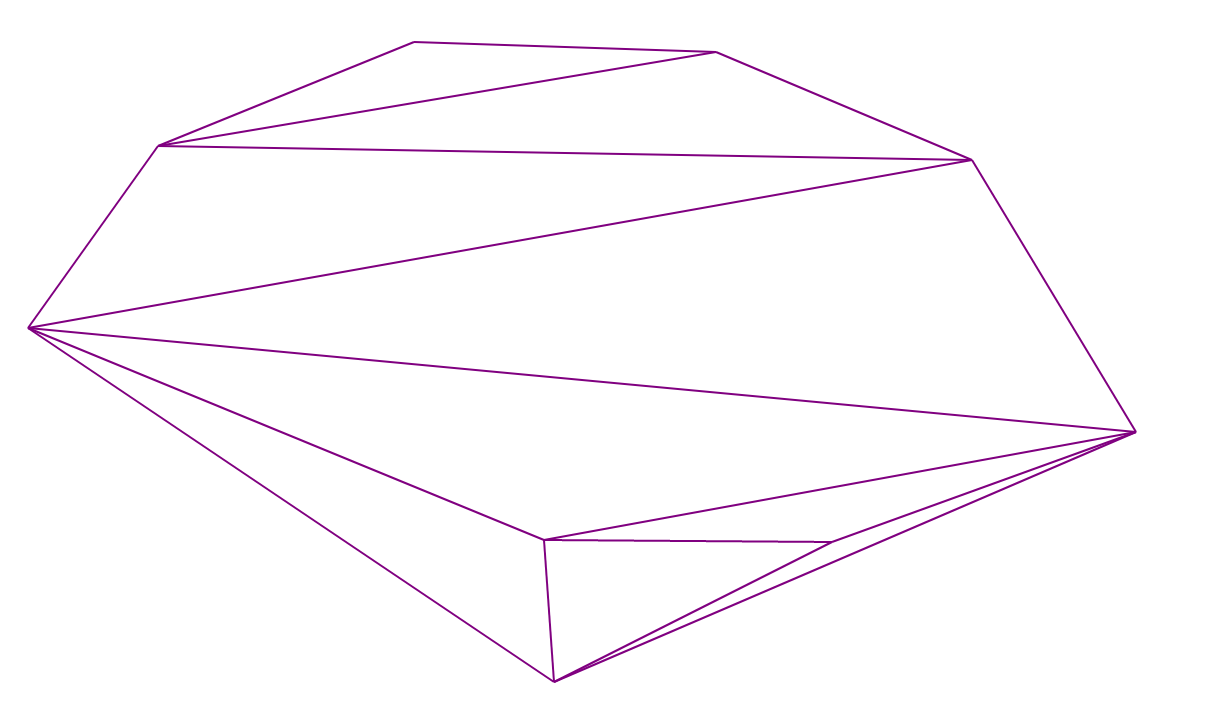
Triangulación de Delaunay

Una triangulación de Delaunay es una triangulación en la que para cualquier triángulo es cierto que no hay puntos del conjunto original dentro del círculo circunscrito a su alrededor.

Nota : para un conjunto dado de puntos en el que no hay 4 puntos en el mismo círculo, hay exactamente una triangulación de Delaunay.

La condición de Delaunay

Deje una triangulación en el conjunto de puntos. Decimos que cierto subconjunto de puntos satisface la condición de Delaunay si la triangulación limitada en este subconjunto es la triangulación de Delaunay para él.

Criterio para la triangulación de Delaunay

El cumplimiento de la condición de Delaunay para todos los puntos que forman un cuadrángulo en una triangulación es equivalente al hecho de que esta triangulación es una triangulación de Delaunay.

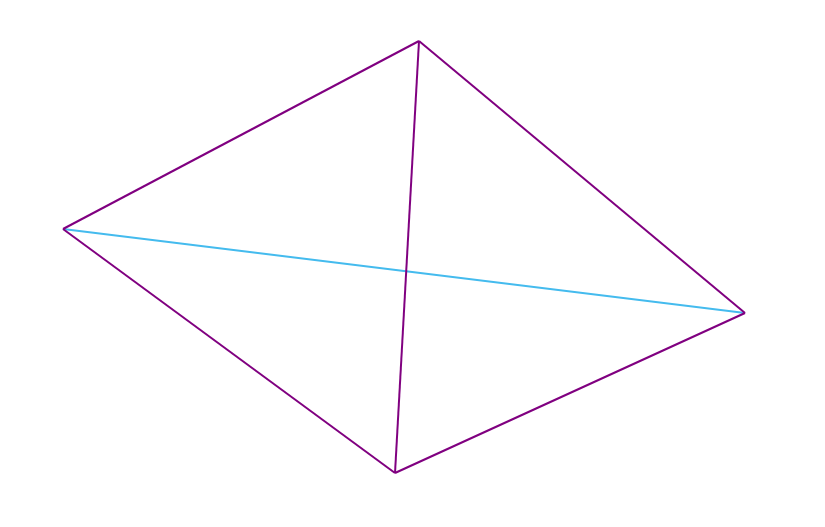
Nota : para los cuadrángulos no convexos, la condición de Delaunay siempre se cumple, y para los cuadrángulos convexos (cuyos vértices no se encuentran en el mismo círculo) hay exactamente 2 triangulaciones posibles (una de las cuales es la triangulación de Delaunay).

La tarea es construir una triangulación de Delaunay para un conjunto dado de puntos.

Descripción del algoritmo

Puntos visibles y bordes visibles.

Deje que se proporcione un casco convexo mínimo (en adelante MBO) de un conjunto finito de puntos (bordes que conectan algunos de los puntos para que formen un polígono que contenga todos los puntos del conjunto) y un punto A que se encuentra fuera del casco. Entonces, el punto del plano se llama visible para el punto A, si el segmento que lo conecta al punto A no se cruza con el MBO.

Un borde MBO se llama visible para el punto A si sus extremos son visibles para A.

En la siguiente imagen, los bordes visibles para el punto rojo están marcados en rojo:

Nota : el contorno de triangulación de Delaunay es el MBO para los puntos en los que está construido.

Observación 2 : en el algoritmo, los bordes visibles para el punto A agregado forman una cadena, es decir, varios bordes MBO en una fila

Almacenar triangulación en la memoria

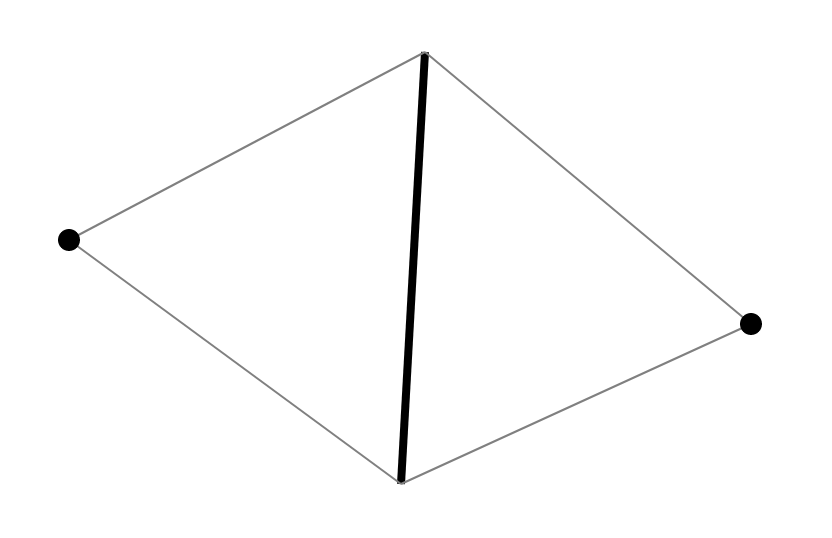
Hay algunos métodos estándar que están bien descritos en el libro de Skvortsov [1]. Debido a los detalles del algoritmo, ofreceré mi propia versión. Como queremos verificar los 4 gones para la condición de Delaunay, consideramos su estructura. Cada cuadrilátero en triangulación es 2 triángulos que tienen un borde común. Cada borde tiene exactamente 2 triángulos adyacentes. Por lo tanto, cada cuadrángulo en la triangulación es generado por un borde y dos vértices opuestos al borde en triángulos adyacentes.
Dado que dos triángulos y su adyacencia se restauran a lo largo del borde y dos vértices, podemos restaurar la triangulación para todas esas estructuras. En consecuencia, se propone almacenar un borde con dos vértices en el conjunto y realizar una búsqueda a lo largo del borde (un par ordenado de vértices).

Algoritmo

La idea de la línea de barrido es que todos los puntos se ordenan en una dirección y luego se procesan por turnos.

1. Ordenar todos los puntos a lo largo de una línea recta (para simplificar, por coordenadas $$$x$)
2. Construimos un triángulo en los primeros 3 puntos.
   
   Además, para cada punto siguiente llevaremos a cabo pasos que preserven la invariante de que hay una triangulación de Delaunay para los puntos ya agregados y, en consecuencia, un MBO para ellos.
3. Agregue los triángulos formados por los bordes visibles y el punto en sí (es decir, agregue los bordes del punto en cuestión a todos los extremos de los bordes visibles).
4. Verificamos en la condición de Delaunay todos los cuadrángulos generados por los bordes visibles. Si en algún lugar la condición no se cumple, entonces reconstruimos la triangulación en el cuadrilátero (recuerdo que solo hay dos de ellos) y ejecutamos de forma recursiva la verificación de los cuadrángulos generados por los bordes del cuadrángulo actual (porque solo después de ellos podría violarse la condición de Delaunay).

Nota : en el paso (4) durante un inicio recursivo, no puede verificar los cuadrángulos generados por los bordes que provienen del punto considerado en esta iteración (siempre hay dos de cada cuatro). La mayoría de las veces no serán convexos, porque la prueba convexa es puramente geométrica, se la dejaré al lector. Además, suponemos que solo se realizan 2 inicios recursivos para cada reconstrucción.

Verificación de una condición de Delaunay

Las formas de probar los cuadrángulos para la condición de Delaunay se pueden encontrar en el mismo libro [1]. Solo noto que al elegir un método con funciones trigonométricas a partir de ahí, con una implementación inexacta, se pueden obtener valores negativos de los senos, tiene sentido tomarlos como módulo.

Buscar bordes visibles

Queda por entender cómo encontrar efectivamente los bordes visibles. Tenga en cuenta que el punto S anterior agregado está en el MBO en la iteración actual, ya que tiene la coordenada más grande $$$x$, y también es visible para el punto actual. Luego, observando que los extremos de los bordes visibles forman una cadena continua de puntos visibles, podemos ir desde el punto S en ambas direcciones a lo largo del MBO y recoger los bordes mientras están visibles (la visibilidad del borde se verifica usando el producto vectorial). Por lo tanto, es conveniente almacenar el MBO como una lista doblemente conectada, en cada iteración eliminando los bordes visibles y agregando 2 nuevos desde el punto considerado.

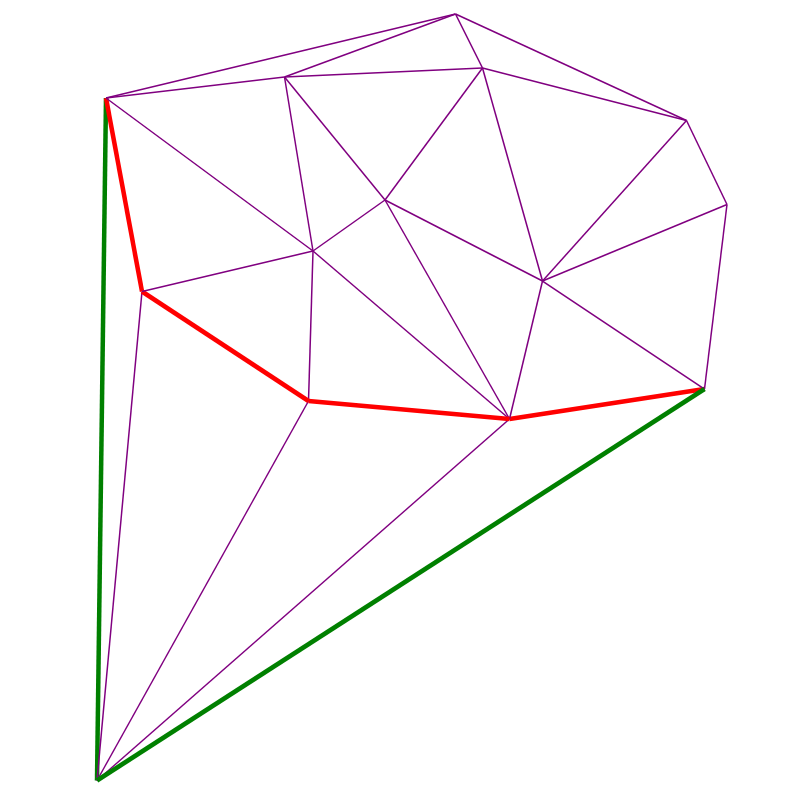
Visualización de algoritmos

Dos puntos rojos: agregado y anterior. Los bordes rojos en cada momento forman la pila de recursión del paso (4):

Algoritmo correcto

Para probar la exactitud del algoritmo, es suficiente probar la conservación de la invariante en los pasos (3) y (4).

Paso (3)

Después del paso (3), obviamente, obtenemos una triangulación del conjunto actual de puntos.

Paso (4)

En el proceso del paso (4), todos los cuadrángulos que no satisfacen la condición de Delaunay están en la pila de recursión (se deduce de la descripción), lo que significa que al final del paso (4) todos los cuadrángulos satisfacen la condición de Delaunay, es decir, la triangulación de Delaunay se construye realmente. Entonces queda por demostrar que el proceso en el paso (4) algún día terminará. Esto se deduce del hecho de que todos los bordes agregados durante la reconstrucción provienen del vértice actual en cuestión (es decir, en el paso $$$k$no hay más que $$$k-1$) y por el hecho de que después de agregar estos bordes no consideraremos los cuadrángulos generados por ellos (ver el comentario anterior), lo que significa que no agregaremos más de una vez.

Complejidad de tiempo

En promedio, el algoritmo funciona bastante bien en distribuciones uniformes y normales (los resultados se muestran en la tabla a continuación). Se supone que su tiempo de trabajo es $$$O (NlogN)$. En el peor de los casos, se realiza una evaluación. $$$O (N ^ 2)$.

Echemos un vistazo al tiempo de trabajo en partes y comprendamos cuál tiene el mayor impacto en el tiempo total:

Ordenar por direccion

Para ordenar, usaremos la estimación $$$O (NlogN)$.

Buscar bordes visibles

Primero, mostramos que el tiempo total dedicado a buscar bordes visibles es $$$O (N)$. Tenga en cuenta que en cada iteración encontramos todos los bordes visibles y 2 más (primero no visible) en tiempo lineal. En el paso (3), agregamos 2 aristas nuevas al MBO. Por lo tanto, en total, no más de $$$2N$costillas, por lo tanto, y varias costillas visibles ya no estarán $$$2N$. También encontraremos $$$2N$bordes que no son visibles. Por lo tanto, en total no hay más $$$4N$costillas que corresponde al tiempo $$$O (N)$.

Construyendo nuevos triángulos

El tiempo total para construir triángulos desde el paso (3) con bordes visibles ya encontrados es obviamente $$$O (N)$.

Reconstruyendo la triangulación

Queda por tratar con el paso (4). Primero, tenga en cuenta que verificar la condición de Delaunay y reconstruir si no se cumple son acciones bastante costosas (aunque funcionan para $$$O (1)$) Solo al comprobar la condición de Delaunay se pueden realizar unas 28 operaciones aritméticas. Veamos el número promedio de reconstrucciones durante este paso. Los resultados prácticos en algunas distribuciones se dan a continuación. Para ellos, realmente quiero decir que el número promedio de reordenamientos crece con una velocidad logarítmica, pero dejemos esto como una suposición.

Aquí también quiero señalar que el número promedio de reordenamientos por punto puede variar mucho de la dirección a lo largo de la cual se realiza la clasificación. Entonces, para un millón distribuido uniformemente en un rectángulo largo y bajo con una relación de aspecto de 100000: 1, este número varía de 1.2 a 24 (estos valores se logran al ordenar los datos horizontal y verticalmente, respectivamente). Por lo tanto, veo el punto de elegir la dirección de clasificación de manera arbitraria (en este ejemplo, con selección arbitraria, se obtuvieron en promedio aproximadamente 2 reconstrucciones) o seleccionarla manualmente si los datos se conocen de antemano.

Por lo tanto, el tiempo principal que el programa suele llevar al paso (4). Si se ejecuta rápidamente, tiene sentido pensar en acelerar la clasificación.

Peor caso

El peor caso en $$$k$se produce la iteración $$$k-1$la llamada recursiva en el paso (4), es decir, sumando todo i, obtenemos el comportamiento asintótico en el peor de los casos $$$O (N ^ 2)$. La siguiente imagen ilustra un hermoso ejemplo en el que el programa puede funcionar durante mucho tiempo (1100 reconstrucciones en promedio al agregar un nuevo punto con una entrada de 10,000 puntos).

Comparación con un algoritmo iterativo para construir una triangulación de Delaunay usando kD-tree

Descripción del algoritmo iterativo.

Describiré brevemente el algoritmo anterior. Cuando llega el siguiente punto, usamos el árbol kD (si no lo sabe, le aconsejo que lo lea en alguna parte), encontramos un triángulo que ya está bastante cerca de él. Luego, evitando en profundidad, buscamos un triángulo, en el que cae el punto. Extendemos los bordes a los vértices del triángulo encontrado y realmente realizamos el paso (4) desde nuestro algoritmo para los nuevos cuadrángulos. Como el punto puede estar fuera de la triangulación, para simplificar se propone cubrir todos los puntos con un triángulo grande (para construirlo de antemano), esto resolverá el problema.

Similitud de algoritmos

De hecho, si los puntos se agregan en orden ordenado por dirección, entonces nuestro algoritmo realmente funciona igual que iterativo, excepto que el número de reordenamientos es menor. La siguiente animación lo demuestra perfectamente. En él, se agregaron puntos de derecha a izquierda, y todos están cubiertos por un triángulo grande, que posteriormente se elimina.

Diferencias de algoritmo

En un algoritmo iterativo, la localización de un punto (búsqueda del triángulo deseado) ocurre en promedio sobre $$$O (logN)$, en las distribuciones anteriores, en promedio, ocurren 3 reordenamientos (como se muestra en [1]) bajo la condición de un orden arbitrario de suministro de puntos. Por lo tanto, la línea de barrido gana el tiempo del algoritmo iterativo en la localización, pero lo pierde en la reconstrucción (lo cual, recuerdo, es bastante difícil). Además, el algoritmo iterativo funciona en línea, que también es su característica distintiva.

Conclusión

Aquí solo muestro algunas triangulaciones interesantes resultantes de la operación del algoritmo.

Hermoso patrón

Distribución normal, 1000 puntos.

Distribución uniforme, 1000 puntos

Triangulación basada en las ubicaciones de todas las ciudades de Rusia.

Aquí puede ver un ejemplo de mi código para este algoritmo:
github.com/Vemmy124/Delaunay-Triangulation-Algorithm

Gracias por su atencion!

Literatura

[1] Skvortsov A.V. La triangulación de Delaunay y su aplicación. - Tomsk: editorial Tom. Universidad, 2002 .-- 128 p. ISBN 5-7511-1501-5