Nos dedicamos a la compra de tráfico de Adwords (una plataforma publicitaria de Google). Una de las tareas habituales en esta área es la creación de nuevos banners. Las pruebas muestran que los banners pierden efectividad con el tiempo, a medida que los usuarios se acostumbran al banner; Las estaciones y las tendencias están cambiando. Además, tenemos el objetivo de capturar diferentes nichos de audiencia, y los banners con un objetivo específico funcionan mejor.

En relación con la entrada en nuevos países, surgió el problema de la localización de pancartas. Para cada banner, debe crear versiones en diferentes idiomas y con diferentes monedas. Puede pedirles a los diseñadores que hagan esto, pero este trabajo manual agregará una carga adicional a un recurso ya escaso.

Parece una tarea fácil de automatizar. Para hacer esto, es suficiente crear un programa que imponga en el banner en blanco un precio localizado para la "etiqueta de precio" y un llamado a la acción (una frase como "comprar ahora") en el botón. Si imprimir texto en una imagen es lo suficientemente simple, entonces determinar dónde debe colocarlo no siempre es trivial. Peppercorns agrega que el botón viene en diferentes colores y tiene una forma ligeramente diferente.

Este artículo está dedicado a: ¿cómo encontrar el objeto especificado en la imagen? Se resolverán los métodos populares; Áreas de aplicación, características, pros y contras. Los métodos anteriores se pueden usar para otros fines: desarrollar programas para cámaras de seguridad, automatización de pruebas de IU y similares. Las dificultades descritas se pueden encontrar en otras tareas, y los métodos utilizados se pueden utilizar para otros fines. Por ejemplo, el Canny Edge Detector se usa a menudo para preprocesar imágenes, y la cantidad de puntos clave se puede usar para evaluar la "complejidad" visual de una imagen.

Espero que las soluciones descritas repongan su arsenal de herramientas y trucos para resolver problemas.

El código está en Python 3.6 ( repositorio ); Se requiere la biblioteca OpenCV. Se espera que el lector comprenda los conceptos básicos de álgebra lineal y visión por computadora.

Nos centraremos en encontrar el botón en sí. Recordaremos sobre encontrar etiquetas de precio (ya que encontrar un rectángulo también se puede resolver de manera más simple), pero omítalo, ya que la solución se verá de la misma manera.

Coincidencia de plantillas

El primer pensamiento que viene a la mente es ¿por qué no elegir y encontrar en la imagen la región que es más similar al botón en términos de diferencia de color de píxeles? Esto es lo que hace que la coincidencia de plantillas sea un método basado en encontrar espacio en la imagen que sea más similar a la plantilla. La "similitud" de una imagen está definida por una métrica específica. Es decir, la plantilla se "superpone" en la imagen, y se considera la discrepancia entre la imagen y la plantilla. La posición de la plantilla en la que esta discrepancia será mínima e indicará la ubicación del objeto deseado.

Puede usar diferentes opciones como métrica, por ejemplo, la suma de las diferencias al cuadrado entre una plantilla y una imagen (suma de las diferencias al cuadrado, SSD), o usar la correlación cruzada (CCORR). Sea fyg la imagen y el patrón con dimensiones (k, l) y (m, n), respectivamente (ignoraremos los canales de color por ahora); i, j : posición en la imagen a la que "adjuntamos" la plantilla.

$$

$$SSD_ {i, j} = \ sum_ {a = 0..m, b = 0..n} {(f_ {i + a, j + b} - g_ {a, b}) ^ 2}$$

$$

$$CCORR_ {i, j} = \ sum_ {a = 0..m, b = 0..n} {(f_ {i + a, j + b} \ cdot g_ {a, b}) ^ 2}$$

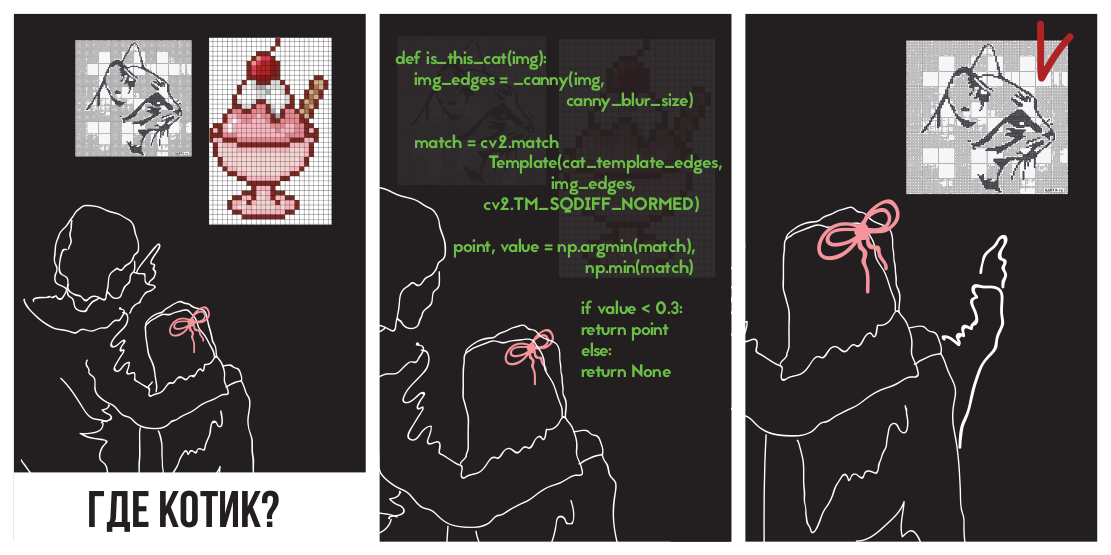
Intentemos aplicar la diferencia de cuadrados para encontrar un gatito

En la foto

(Fotografía tomada de PETA Caring for Cats).

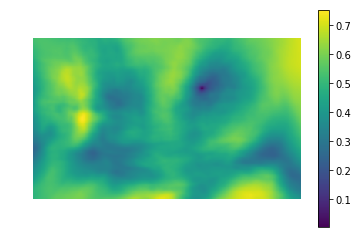
La imagen de la izquierda es el valor métrico de la similitud del lugar en la imagen con la plantilla (es decir, los valores de SSD para diferentes i, j). El área oscura es el lugar donde la diferencia es mínima. Este es un puntero al lugar que más se parece a una plantilla; en la imagen de la derecha, este lugar está rodeado.

La correlación cruzada es en realidad una convolución de dos imágenes. Las convoluciones se pueden implementar rápidamente utilizando la rápida transformación de Fourier. Según el teorema de convolución, después de la transformada de Fourier, la convolución se convierte en una simple multiplicación por elementos:

$$

$$CCORR_ {i, j} = f \ circledast g = IFFT (FFT (f \ circledast g)) = IFFT (FFT (f) \ cdot FFT (g))$$

Donde $$$\ circledast$ - operador de convolución. De esta forma podemos calcular rápidamente la correlación cruzada. Esto proporciona la complejidad general de O (kllog (kl) + mnlog (mn)) , frente a O (klmn) cuando se implementa de frente. El cuadrado de la diferencia también se puede realizar mediante convolución, ya que después de abrir los corchetes se convertirá en la diferencia entre la suma de los cuadrados de los valores de píxeles de la imagen y la correlación cruzada:

$$

$$SSD_ {i, j} = \ sum_ {a = 0..m, b = 0..n} {(f_ {i + a, j + b} - g_ {a, b}) ^ 2} =$$

$$

$$= \ sum_ {a = 0..m, b = 0..n} {f_ {i + a, j + b} ^ 2 - 2 f_ {i + a, j + b} g_ {a, b} + g_ {a, b} ^ 2} =$$

$$

$$= \ sum_ {a = 0..m, b = 0..n} {f_ {i + a, j + b} ^ 2 + g_ {a, b} ^ 2} - 2CCOR_ {i, j}$$

Los detalles se pueden ver en esta presentación .

Pasemos a la implementación. Afortunadamente, los colegas del departamento de Intel de Nizhny Novgorod se encargaron de nosotros al crear la biblioteca OpenCV, que ya implementa una búsqueda de una plantilla utilizando el método matchTemplate (por cierto, utiliza la implementación FFT, aunque esto no se menciona en la documentación), utilizando diferentes métricas de discrepancia :

• CV_TM_SQDIFF: la suma de los cuadrados de la diferencia en valores de píxeles
• CV_TM_SQDIFF_NORMED: la suma del cuadrado de las diferencias de color, normalizado al rango 0..1.
• CV_TM_CCORR: la suma de los productos elemento por elemento de la plantilla y el segmento de imagen
• CV_TM_CCORR_NORMED: la suma del elemento funciona, normalizada al rango -1..1.
• CV_TM_CCOEFF: correlación cruzada de imágenes sin promedio
• CV_TM_CCOEFF_NORMED - correlación cruzada entre imágenes sin un promedio, normalizado a -1..1 (correlación de Pearson)

Los usaremos para encontrar un gatito:

Se puede ver que solo TM_CCORR no hizo frente a su tarea. Esto es comprensible: dado que es un producto escalar, el mayor valor de esta métrica será al comparar una plantilla con un rectángulo blanco.

Puede notar que estas métricas requieren una coincidencia de patrón de píxel por píxel en la imagen deseada. Cualquier desviación de gamma, luz o tamaño dará como resultado que los métodos no funcionen. Permítame recordarle que este es exactamente nuestro caso: los botones pueden ser de diferentes tamaños y colores.

El problema de los diferentes colores y luces se puede resolver aplicando un filtro de detección de bordes. Este método solo deja información sobre dónde en la imagen hubo cambios bruscos de color. Apliquemos Canny Edge Detector (lo analizaremos un poco más) a los botones de diferentes colores y brillo. A la izquierda están los banners originales, y a la derecha está el resultado de aplicar el filtro Canny.

En nuestro caso, también hay un problema de diferentes tamaños, pero ya se ha resuelto. La transformación logarítmica polar transforma una imagen en un espacio en el que el zoom y la rotación aparecerán como un desplazamiento. Usando esta transformación, podemos restaurar la escala y el ángulo. Después de eso, al escalar y rotar la plantilla, puede encontrar la posición de la plantilla en la imagen original. También puede usar FFT a lo largo de este procedimiento, como se describe en Una técnica basada en FFT para traducción, rotación y registro de imagen invariante a escala . En la literatura, el caso se considera cuando los patrones horizontales y verticales se cambian proporcionalmente, mientras que el factor de escala varía dentro de límites pequeños (2.0 ... 0.8). Desafortunadamente, cambiar el tamaño de un botón puede ser grande y desproporcionado, lo que puede conducir a un resultado incorrecto.

Aplicamos la construcción resultante (filtro Canny, restaurando solo la escala a través de la transformación logarítmica polar, obteniendo la posición mediante la búsqueda del lugar con la mínima discrepancia cuadrática), para encontrar el botón en tres imágenes. Utilizaremos el botón amarillo grande como plantilla:

Al mismo tiempo, los botones en los banners serán de diferentes tipos, colores y tamaños:

En el caso de cambiar el tamaño del botón, el método no funcionó correctamente. Esto se debe al hecho de que el método implica cambiar el tamaño de los botones en la misma cantidad de veces, tanto horizontal como verticalmente. Sin embargo, este no es siempre el caso. En la imagen de la derecha, el tamaño del botón no ha cambiado verticalmente, pero horizontalmente ha disminuido considerablemente. Si el cambio de tamaño es demasiado grande, las distorsiones causadas por la transformación logarítmica polar hacen que la búsqueda sea inestable. En este sentido, el método no pudo detectar el botón en el tercer caso.

Detección de puntos clave

Puede intentar un enfoque diferente: en lugar de buscar el botón completo, busquemos sus partes típicas, por ejemplo, las esquinas del botón o los elementos del borde (hay un trazo decorativo a lo largo del contorno del botón). Parece que encontrar esquinas y un borde es más fácil, ya que estos son objetos pequeños (y por lo tanto simples). Lo que se encuentra entre las cuatro esquinas y el borde será un botón. La clase de métodos para encontrar puntos clave se denomina "detección de puntos clave", y los algoritmos para comparar y buscar imágenes utilizando puntos clave se denominan "coincidencia de puntos clave". La búsqueda de un patrón en una imagen se reduce a aplicar un algoritmo para detectar puntos clave en un patrón y una imagen, y comparar los puntos clave de un patrón y una imagen.

Por lo general, los "puntos clave" se encuentran automáticamente al encontrar píxeles cuyo entorno tiene ciertas propiedades. Se inventaron muchos métodos y criterios para encontrarlos. Todos estos algoritmos son heurísticos que encuentran algunos elementos característicos de la imagen, por regla general: ángulos o cambios bruscos de color. Un buen detector debería funcionar rápidamente y ser resistente a las transformaciones de la imagen (al cambiar la imagen, los puntos clave no deben dejar de estar / moverse).

Detector de esquina Harris

Uno de los algoritmos más básicos es el detector de esquina Harris . Para la imagen (en adelante consideramos que estamos operando con "intensidad", una imagen traducida a escala de grises), trata de encontrar puntos en los alrededores de los cuales las diferencias de intensidad son mayores que un cierto umbral. El algoritmo se ve así:

1. De intensidad $$$I$ son derivados a lo largo de los ejes x e y ( $$$I_x$ y $$$I_y$ respectivamente). Se pueden encontrar, por ejemplo, aplicando el filtro Sobel.

   
   

2. Para un píxel, considere el cuadrado $$$I_x$ plaza $$$I_y$ y funciona $$$I_x$ y $$$I_y$ . Algunas fuentes los etiquetan como $$$I_ {xx}$ , $$$I_ {xy}$ y $$$I_ {xy}$ - lo cual no agrega claridad, ya que uno podría pensar que estas son las segundas derivadas de la intensidad (y esto no es así).

   
   

3. Para cada píxel, consideramos las sumas en un vecindario determinado (más de 1 píxel) con las siguientes características:

   $$

   $$A = \ sum_ {x, y} {w (x, y) I_xI_x}$$
   
   

   $$

   $$B = \ sum_ {x, y} {w (x, y) I_xI_y}$$
   
   

   $$

   $$C = \ sum_ {x, y} {w (x, y) I_yI_y}$$
   
   Al igual que en la detección de plantillas, este procedimiento para ventanas grandes se puede llevar a cabo de manera eficiente utilizando el teorema de convolución.
   

4. Para cada píxel, calcule el valor $$$^ \ star$ R heurística

   $$

   $$R = Det (H) - k (Tr (H)) ^ 2 = (AB - C ^ 2) - k (A + B) ^ 2$$
   
   Valor $$$k$ seleccionado empíricamente en el rango [0.04, 0.06] Si $$$R$ algunos píxeles tienen un cierto umbral, entonces el vecindario $$$w$ Este píxel contiene un ángulo, y lo marcamos como un punto clave.
   

5. La fórmula anterior puede crear grupos de puntos clave uno al lado del otro, en cuyo caso vale la pena eliminarlos. Esto se puede hacer comprobando para cada punto si tiene un valor $$$R$ Máximo entre vecinos inmediatos. Si no, entonces el punto clave se filtra. Este procedimiento se llama supresión no máxima .

   
   

$$$\ star$ Formula $$$R$ elegido por una razón $$$A, B, C$ - componentes del tensor estructural - matriz que describe el comportamiento del gradiente en la vecindad:

$$

$$H = \ begin {pmatrix} A y C \\ C & B \ end {pmatrix}$$

Esta matriz es similar en muchos aspectos a su matriz de covarianza. Por ejemplo, ambas son matrices positivamente semidefinidas, pero la similitud no se limita a esto. Permíteme recordarte que la matriz de covarianza tiene una interpretación geométrica. Los vectores propios de la matriz de covarianza indican las direcciones de la mayor varianza de los datos de origen (sobre los cuales se calculó la covarianza), y los valores propios indican la dispersión a lo largo del eje:

Imagen tomada de http://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix/

Los valores propios del tensor estructural también se comportan de la misma manera: describen la propagación de los gradientes. En una superficie plana, los valores propios del tensor estructural serán pequeños (porque la extensión de los propios gradientes será pequeña). Los valores propios del tensor estructural construido en una pieza de una imagen con una cara variarán mucho: un número será grande (y corresponderá a su propio vector dirigido perpendicular a la cara), y el segundo será pequeño. En el tensor de ángulo, ambos valores propios serán grandes. En base a esto, podemos construir una heurística ( $$$\ lambda_1, \ lambda_2$ Son los valores propios del tensor estructural).

$$

$$R = \ lambda_1 \ lambda_2 - k (\ lambda_1 + \ lambda_2) ^ 2$$

El valor de esta heurística será grande cuando ambos valores propios son grandes.

La suma de los valores propios es la traza de la matriz, que puede calcularse como la suma de los elementos en la diagonal (y si observa las fórmulas A y B, queda claro que esta también es la suma de los cuadrados de las longitudes de los gradientes en la región):

$$

$$\ lambda_1 + \ lambda_2 = Tr (H) = A + B$$

El producto de los valores propios es el determinante de una matriz, que también es fácil de escribir en el caso de 2x2:

$$

$$\ lambda_1 \ lambda_2 = Det (H) = AB - C ^ 2$$

Por lo tanto, podemos calcular efectivamente $$$R$ , expresándolo en términos de los componentes del tensor estructural.

Rápido

El método de Harris es bueno, pero hay muchas alternativas. No consideraremos todo de la misma manera que el método anterior, solo mencionaremos algunos populares para mostrar trucos interesantes y compararlos en acción.

Píxeles verificados por el algoritmo FAST

Una alternativa al método de Harris es RÁPIDO . Como su nombre indica, FAST es mucho más rápido que el método anterior. Este algoritmo intenta encontrar los puntos que se encuentran en los bordes y esquinas de los objetos, es decir. en lugares de diferencia de contraste. Su ubicación es la siguiente: FAST construye un círculo de radio R alrededor del píxel candidato y comprueba si tiene un segmento continuo de píxeles de longitud t que es más oscuro (o más claro) del píxel candidato por K unidades. Si se cumple esta condición, el píxel se considera un "punto clave". Para ciertas t, podemos implementar esta heurística de manera eficiente agregando algunas comprobaciones preliminares que cortarán los píxeles que se garantiza que no son esquinas. Por ejemplo, cuando $$$R = 3$ y $$$t = 12$ , es suficiente para verificar si hay 3 píxeles consecutivos entre los 4 píxeles extremos que son estrictamente más oscuros / claros que el centro en K (en la imagen: 1, 5, 9, 13). Esta condición le permite cortar efectivamente a los candidatos que definitivamente no son puntos clave.

SIFT

Ambos algoritmos anteriores no son resistentes al cambio de tamaño de la imagen. No le permiten encontrar una plantilla en la imagen si la escala del objeto ha cambiado. SIFT (transformación de características invariantes de escala) ofrece una solución a este problema. Tome la imagen de la que extraemos los puntos clave y comience a reducir gradualmente su tamaño con un pequeño paso, y para cada opción de escala encontraremos los puntos clave. El escalado es un procedimiento difícil, pero reducirlo en 2/4/8 / ... veces se puede hacer de manera eficiente saltando píxeles (en SIFT estas escalas múltiples se denominan "octavas"). Las escalas intermedias se pueden aproximar aplicando un azul gaussiano con un tamaño de núcleo diferente a la imagen. Como describimos anteriormente, esto puede hacerse computacionalmente de manera eficiente. El resultado se verá si primero redujimos la imagen y luego la ampliamos a su tamaño original: se pierden pequeños detalles y la imagen se vuelve "borrosa".

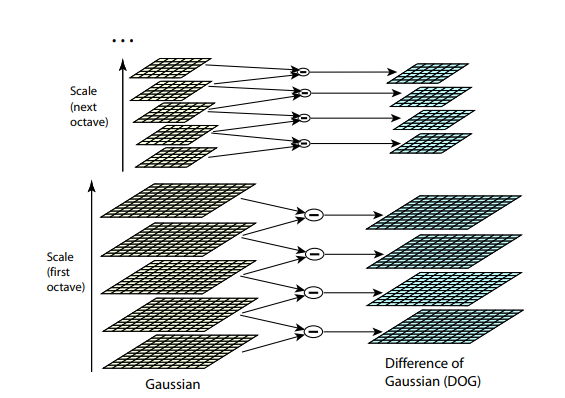
Después de este procedimiento, calculamos la diferencia entre escalas vecinas. Los valores grandes (en valor absoluto) en esta diferencia se obtendrán si alguna parte pequeña deja de ser visible en el siguiente nivel de escala, o, por el contrario, el siguiente nivel de escala comienza a capturar alguna parte que no era visible en el anterior. Esta técnica se llama DoG, Diferencia de Gauss. Podemos suponer que la gran importancia de esta diferencia ya es una señal de que hay algo interesante en este lugar en la imagen. Pero estamos interesados ​​en la escala para la cual este punto clave será más expresivo. Para hacer esto, consideraremos un punto clave no solo como un punto que difiere de su entorno, sino que también difiere más fuertemente entre las diferentes escalas de imagen. En otras palabras, elegiremos un punto clave no solo en el espacio X e Y, sino en el espacio $$$(X, Y, Escala)$ . En SIFT, esto se hace mediante la búsqueda de puntos en la DoG (Diferencia de gaussianos), que son máximos o mínimos locales en $$$3x3x3$ cubo de espacio $$$(X, Y, Escala)$ a su alrededor

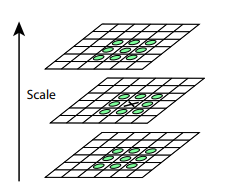
Los algoritmos para encontrar puntos clave y construir descriptores SIFT y SURF están patentados. Es decir, para su uso comercial es necesario obtener una licencia. Es por eso que no están disponibles en el paquete principal de opencv, sino solo en un paquete separado de opencv_contrib. Sin embargo, hasta ahora nuestra investigación es de naturaleza puramente académica, por lo tanto, nada nos impide participar en el SIFT en comparación.

Descriptores

Intentemos aplicar algún tipo de detector (por ejemplo, Harris) a la plantilla y a la imagen.

Después de encontrar los puntos clave en la imagen y la plantilla, debe compararlos de alguna manera entre sí. Permítame recordarle que hasta ahora solo hemos extraído las posiciones de los puntos clave. Lo que significa este punto (por ejemplo, en qué dirección se dirige el ángulo encontrado), aún no lo hemos determinado. Y tal descripción puede ayudar al comparar puntos de imagen y patrones entre sí. Algunos de los puntos de la plantilla en la imagen pueden ser desplazados por distorsiones, cubiertos por otros objetos, por lo que depender únicamente de la posición de los puntos entre sí parece poco confiable. Por lo tanto, tomemos su vecindario para cada punto clave para construir una determinada descripción (descriptor), que luego nos permite tomar un par de puntos (un punto de la plantilla, uno de la imagen), y comparar su similitud.

BREVE

(.. 0 1), , XOR , . ? , N . , i- , , — i- 1. N. - (, — ), : , “”. , ( ). BRIEF .

. . , GII .

, , (.. , , ). OpenCV .

SIFT

SIFT , . SIFT 1616 , 44 . ( , ). 8 (, -, , ..). — 8 , , . . , 8- . 128 ( 4*4 = 16 , 8 ). .

Comparación

( — , ), - :

— . ?

, . , , . , , , , . ? BRIEF, , , . , BRIEF 1/16 . SIFT — - 1/4 .

SIFT.

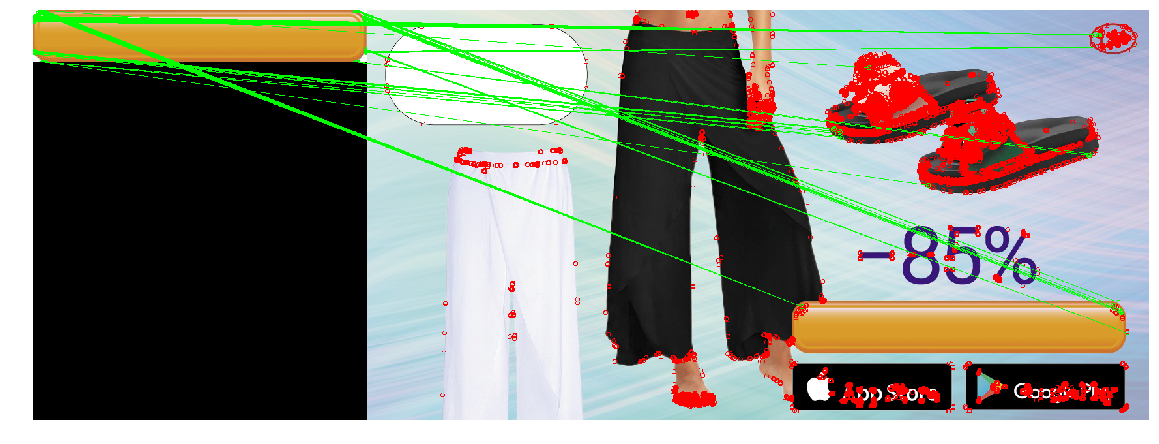
Ahora aplicamos todo el conocimiento adquirido para resolver nuestro problema. En nuestro caso, los requisitos para el detector de punto clave son suficientes: no necesitamos invariancia para cambiar el tamaño, así como un rendimiento extremadamente alto. Compara los tres detectores.

Detector de esquina Harris	Rápido	SIFT

SIFT encontró muy pocos puntos clave en el botón. Esto es comprensible: el botón es un objeto bastante pequeño y plano, y el zoom no ayuda a encontrar puntos clave.

Además, ni un solo detector manejó el tercer caso. Esto es explicable y esperado. Por lo general, los métodos anteriores se utilizan para encontrar un objeto de una plantilla en una imagen en la que se puede ocultar, rotar o distorsionar parcialmente. En nuestro caso, queremos encontrar no exactamente el mismo objeto , sino un objeto que sea bastante similar a la plantilla (botón) . Esta es una tarea ligeramente diferente. Por lo tanto, al cambiar la forma del botón en sí (por ejemplo, el radio de redondeo de las esquinas, o el grosor del marco de puntos) cambia los puntos clave en ellos y sus descriptores. Además, los puntos clave se ubicarán en la esquina del botón. Debido a la posición en el borde, los puntos serán inestables: su ubicación exacta y los descriptores se ven afectados por lo que se dibuja al lado del botón.

Conclusión: el método es bueno y cumple correctamente situaciones en las que se gira el objeto deseado, se cambia su tamaño o el objeto está parcialmente oculto (lo cual es bueno para encontrar objetos complejos o una etiqueta de precio, por ejemplo). Sin embargo, si hay pocos puntos en el objeto que pueden ser "atrapados", o la forma del objeto cambia demasiado, entonces los puntos clave y ellos en la plantilla y la imagen pueden no coincidir. Además, un fondo con muchos detalles pequeños puede cambiar los "puntos clave" o cambiar sus descriptores.

Podemos encontrar una coincidencia que use las coordenadas de los puntos clave. En lugar de buscar pares de puntos en la plantilla y la imagen, cuyo vecindario es similar, puede buscar dichos conjuntos de puntos, la interposición de puntos clave en la plantilla y la imagen será similar. En el caso general, esta es una tarea bastante complicada (tanto computacionalmente como desde un punto de vista de programación), especialmente en una situación en la que algunos puntos pueden ser cambiados o ausentes. Pero, dado que tenemos puntos clave - ángulos, es suficiente para nosotros encontrar grupos que aproximadamente formarán un rectángulo de las proporciones deseadas, y dentro del cual no habrá puntos clave. Poco a poco llegamos al siguiente método:

Detección de contorno

Por lo general, un botón es algún tipo de objeto rectangular (a veces con esquinas redondeadas), cuyos lados son paralelos a los ejes de coordenadas. Luego, intentemos distinguir las zonas de diferencia de contraste (bordes), y entre ellas encontraremos caras cuyos contornos son similares al contorno del objeto que necesitamos. Este método se llama detección de contorno.

Detección de bordes

A diferencia de la detección de puntos clave, estamos interesados ​​no solo en los ángulos de los puntos clave, sino también en los bordes. Sin embargo, las ideas básicas que podemos tomar de allí. Alise la imagen con un filtro gaussiano, y como en el detector de esquina Harris. Luego calculamos las derivadas de la intensidad $$$I_x$ y $$$I_y$ . Dado que no necesitamos distinguir los ángulos de los bordes, no necesitamos considerar el tensor estructural; es suficiente para calcular la fuerza del gradiente: $$$I_l = I_x ^ 2 + I_y ^ 2$ (por cierto, esta es la raíz de $$$Tr (H)$ , o de la suma de la diagonal del tensor estructural). Después de eso, dejamos solo píxeles que son máximos locales en términos de $$$I_l$ (utilizando la supresión no máxima ya considerada), pero como configuración regional elegiremos no 8 píxeles vecinos, sino aquellos píxeles de estos 8, a los que me dirijo, y del lado opuesto:

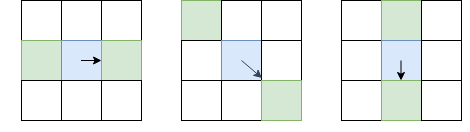
El píxel en cuestión es azul, la flecha es la dirección I. Los píxeles verdes son los que se tendrán en cuenta durante la supresión no máxima.

Una elección tan inusual de píxeles para la comparación se debe al hecho de que no queremos hacer huecos en el borde. En la imagen de la izquierda, la cara va de arriba a abajo, y dado que la supresión no máxima no comparará las intensidades con los píxeles arriba y abajo del azul, obtenemos una cara continua.

Obviamente, una supresión no máxima no es suficiente, y debe aplicar algún tipo de filtrado para eliminar bordes con un Il demasiado bajo. Para hacer esto, aplicamos la técnica de "doble umbral": eliminamos todos los píxeles con Il, con una intensidad de gradiente por debajo del umbral bajo, y asignamos todos los píxeles por encima del umbral alto para que sean "bordes fuertes". Los píxeles en los que la intensidad del gradiente se encuentra entre Bajo y Alto se denominarán "bordes débiles", solo los dejamos si están conectados a "bordes fuertes":

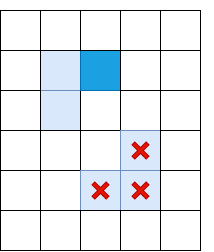
Azul claro indica "costillas débiles", azul oscuro - fuerte. Las costillas en la parte inferior están cernidas, ya que no están conectadas a ninguna costilla fuerte.

Acabamos de describir Canny Edge Detector. Es extremadamente utilizado hasta el día de hoy como un procedimiento simple y rápido que le permite encontrar los contornos de los objetos.

Seguimiento de la frontera

La siguiente acción es seleccionar los contornos entre el mapa con las caras encontradas. Encuentre los componentes relacionados (islas de píxeles adyacentes que han pasado todas las comprobaciones) y compruebe cada uno de ellos, cuánto se parece a un botón. Después de aplicar la supresión no máxima en Canny, tenemos garantías de que los bordes tendrán un grosor de un píxel, pero confiemos en ello. Para cada píxel que se asignó a una cara, y al lado del cual hay un píxel que no es de cara, lo asignamos a un "borde". Pasando de un píxel del borde a otro, volvemos al mismo píxel (y luego encontramos el camino), o a un callejón sin salida (entonces puede intentar regresar si había una bifurcación en algún lugar del camino):

Aquí se describe el algoritmo de seguimiento de borde completo, teniendo en cuenta diferentes casos de borde (por ejemplo, cuando un objeto con una cara gruesa genera dos contornos, interno y externo). Después de aplicar este algoritmo, tendremos un conjunto de contornos que podrían ser botones.

Filtrado de ruta

¿Cómo saber que nuestro circuito es un botón? Para rectángulos y polígonos hay un excelente método basado en simplificar el contorno . Es suficiente con "colapso" gradual de las costillas, si están casi en línea recta, y luego calcular el número de costillas restantes y verificar los ángulos entre ellas. Desafortunadamente, para nuestro caso, estos métodos no son adecuados: nuestro rectángulo tiene esquinas redondeadas. Además, hay coincidencia de contornos para figuras con geometría compleja, pero esto tampoco se trata de nosotros, ya que solo tenemos un rectángulo (en el artículo se dan ejemplos con un contorno humano). Por lo tanto, es mejor hacer un filtro basado en las propiedades de la figura misma. Sabemos que:

• El botón es lo suficientemente grande (área de más de 100 píxeles)
• Los lados son paralelos a los ejes de coordenadas.
• La relación del área de la figura al área del rectángulo delimitador debe estar bastante cerca de la unidad. Establecemos el umbral en 0.8, ya que el botón es un rectángulo con lados paralelos a los ejes de coordenadas, y el 20% que falta son las esquinas redondeadas.

Además, por la experiencia de usar detectores de puntos clave, recordamos que puede haber problemas con situaciones en las que hay un objeto de contraste debajo del botón. Por lo tanto, después de aplicar Canny, desenfocamos los bordes para cerrar pequeños agujeros que podrían surgir de tales objetos.

Aplicamos el enfoque resultante:

La aplicación de filtro Canny (imagen 2) encontró la forma necesaria, pero debido a la forma compleja del botón y el gradiente, se encontraron muchos contornos a la vez, y debido a la supresión no máxima, algunos de ellos no se cerraron. La aplicación de desenfoque (imagen 3) solucionó el problema.

Enfoque de prueba

Ejecute la búsqueda de contornos en la imagen resultante. Colorea los contornos que pasaron la prueba en rojo. Si hay varios de ellos, entonces debemos elegir la opción más exitosa entre ellos. Seleccionamos el contorno del área más grande y lo pintamos de verde.

El | El | El | El |

El diseño resultante encontró botones en las imágenes de prueba. Una ejecución en todos los banners mostró que ocasionalmente (1 caso de ~ 20), en lugar de un botón, selecciona mosaicos rectangulares de iOS Appstore y Google Apps, u otros objetos rectangulares (cajas del teléfono). Por lo tanto, agregando la capacidad de indicar manualmente la posición en ese raro caso de una determinación incorrecta, implementamos esta opción en la herramienta de localización.

Conclusión

Para resumir. El CV "clásico" sin aprendizaje profundo todavía funciona, y en base a él puedes resolver problemas. No son pretenciosos y no requieren una gran cantidad de datos etiquetados, hardware potente, y son más fáciles de depurar. Sin embargo, introducen suposiciones adicionales y, por lo tanto, con su ayuda, no todos los problemas se pueden resolver de manera efectiva.

• La coincidencia de plantillas es la forma más fácil, basada en encontrar un lugar en la imagen que sea más similar (por alguna métrica simple) a una plantilla. Efectivo con la comparación píxel por píxel. Puede hacerse resistente a las curvas y pequeños cambios de tamaño, pero con grandes cambios puede que no funcione correctamente.
• Detección / coincidencia de puntos clave: encuentre los puntos clave, haga coincidir los puntos de la imagen y la plantilla. Los detectores son resistentes a las rotaciones, al zoom (según el detector y descriptor seleccionados) y a la coincidencia, a solapamientos parciales. Pero este método funciona bien solo si hay suficientes "puntos clave" en el objeto, y los locales de la plantilla y los puntos de imagen coinciden bastante bien (es decir, el mismo objeto en la plantilla y la imagen).
• Detección de contorno : encontrar los contornos de los objetos y encontrar un contorno similar al contorno del objeto deseado. Esta solución solo tiene en cuenta la forma del objeto e ignora su contenido y color (que puede ser tanto un más como un menos).
  Un lector experto puede notar que nuestro problema puede resolverse con la ayuda de métodos modernos de visión por computadora capacitados. Por ejemplo, la red YOLO devuelve el cuadro delimitador del objeto deseado, y esto es lo que nos interesa. Sí, probamos y lanzamos con éxito la solución basada en el aprendizaje profundo, pero como una segunda iteración (ya después de que se lanzó la herramienta de localización y comenzó a funcionar). Estas soluciones son más resistentes a los cambios en los parámetros de los botones y tienen muchas propiedades positivas: por ejemplo, en lugar de seleccionar umbrales y parámetros con las manos, simplemente puede agregar ejemplos de banners en los que la red está equivocada (Aprendizaje activo) en el conjunto de entrenamiento. Usar el aprendizaje profundo para nuestra tarea tiene sus problemas y puntos interesantes. Por ejemplo, muchos métodos modernos de visión por computadora requieren una gran cantidad de imágenes marcadas, pero no teníamos marcado (como en muchos casos reales), y el número total de diferentes banners no excede varios miles. Por lo tanto, decidimos diseñar una pequeña cantidad de imágenes nosotros mismos y escribir un generador que creará otros banners similares sobre la base de ellos. En esta dirección hay muchos trucos interesantes . Hay muchas otras trampas, y la tarea misma de determinar la posición de un objeto de visión por computadora es extensa y tiene muchas soluciones. Por lo tanto, se decidió limitar el campo de visión del artículo y no se consideraron las decisiones basadas en el aprendizaje profundo.

El código con blocs de notas que implementan los métodos descritos y dibuja imágenes del artículo se puede encontrar en el repositorio ).