Es más difícil escribir sobre matemáticas (por lo que es interesante) que sobre física. Sin embargo, espero que leas al menos los ejemplos de locos programas de C.
Los monstruos pueden surgir de cosas completamente inofensivas. Tomemos, por ejemplo, el juego de las subcadenas. Escribimos una cadena de letras ayb y seleccionamos las subcadenas del carácter 1 al carácter 2, del 2 al 4, del tres al 6, de n a 2n, hasta que la longitud de la cadena principal sea suficiente. Nuestra tarea es asegurarnos de que en estas subcadenas el más corto no entre más. Incluso escribí un analizador SQL:
declare @s varchar(max) = 'abbbaaaaaaab' declare @n int=1 declare @sub table (n int, sub varchar(max)) while @n*2<=len(@s) begin insert into @sub select @n,substring(@s,@n,@n+1) set @n=@n+1 end select *,(select max(sub) from @sub I where In>On and charindex(O.sub,I.sub)>0) as FoundMatch from @sub O order by 1
Aquí hay un ejemplo de salida:
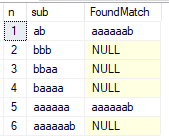
Como puede ver, las subcadenas 1 y 5 no pasaron la prueba. Podemos eliminar el último carácter, y la cadena de 11 caracteres resultante 'abbbaaaaaaaa' pasará la prueba. Resulta que esta es la cadena más larga posible en el alfabeto de dos caracteres que satisface esta condición.
Para un alfabeto de un carácter, la longitud máxima de la cadena es 3, y luego por razones puramente técnicas. Resulta que la longitud máxima es finita para un alfabeto de cualquier número de letras. Entonces tenemos:
f(1)=3
f(2)=11
f(3)=???$
Pon a prueba tu intuición sobre cuánto tiempo se puede hacer una cadena en un alfabeto de tres letras. 100? 1000? De hecho, mucho más que Googol, y mucho más que GoogolPlekh.
f(3)>2 uparrow7198158836
Y tengo que pasar tiempo para mostrar la fuerza de los tiradores.
Flechas (hiperoperación)
Usamos la multiplicación para no escribir muchas operaciones de suma:
2∗5=2+2+2+2+2
Usamos exponenciación para no escribir muchas multiplicaciones:
23=2∗2∗2
Considerando la suma como una operación de nivel 0, la multiplicación como 1, la exponenciación como 2, podemos introducir la operación "flecha", por ejemplo,
3 uparrow3=3(33)=327=7′625′597′484′987
Tenga en cuenta que los paréntesis ya son importantes aquí. El siguiente nivel es la operación de dos flechas:
3 uparrow uparrow3=3 uparrow(3 uparrow3)=3 uparrow7625597484987=33...3
La última pirámide de triples tiene una altura de 7 mil millones, y este número ya es mucho, mucho mayor que googol y googolpleks. Denotamos este gran número como
Oscuridad (era un número tal en el antiguo idioma ruso) e intentamos dar un paso más:
3 uparrow33=3 uparrow uparrow uparrow3=3 uparrow uparrow(3 uparrow uparrow3)=3 uparrow uparrowoscuridad=3 uparrow3 uparrow3... uparrow3
(y tantas veces) ... Ya se imagina qué tan grande es este número. Tenga en cuenta que cuando hay muchas flechas, escribimos un repetidor en la parte superior. Entonces puedes entender lo genial
f(3)>2 uparrow7198158836
Y mas
Usando flechas, solo se crea el más pequeño de los números grandes, por así decirlo. La tasa de crecimiento de las funciones se mide en cierta escala, comparándola con
funciones de rápido crecimiento . La primera función en esta jerarquía corresponde a la suma, la segunda a la multiplicación, la tercera a la flecha y las flechas n-ésima a n-2 (aproximadamente, no exactamente). Pero puedes definir
fw(n)=fn(n)
Dicha función para n = 3 es comparable con una flecha, para n = 4 con dos flechas y, a medida que el parámetro n crece, supera el crecimiento de la función con cualquier número estático de flechas.
Puedes ir aún más lejos:
fw,fw+1,fw+n,fw2,fw2,fww,fwww,f epsilon Estas funciones están indexadas por ordinales, o en la literatura rusa por números ordinales. La imagen con la estructura de los números ordinales iniciales precede al artículo, pero se extienden mucho más y comienza
Poco misticismo
La infinita pirámide de omega da un ordinal
e p s i l o n 0 . Lea sobre la
función cuyo crecimiento se mide con este ordinal. ¡Resulta que una función crece tan rápido que la aritmética formal no puede, en principio, probar que dicha función está definida en absoluto!
Por supuesto, usted sabe sobre el teorema de Godel de que hay declaraciones que no se pueden probar. Pero, como regla, el único ejemplo de tal declaración es la construcción de Gödel en sí misma ("No soy demostrable"). El teorema de Goodstein es un buen ejemplo de tal afirmación.
Además, resulta que los ordinales de alguna manera
miden el poder de las teorías . La "fuerza" de la aritmética formal es
e p s i l o n 0 , la
teoría de conjuntos simplificada de Kripke-Plateka tiene la fuerza del
ordinal de Feferman-Schutte , etc.
Tin - torniquete de matemáticas - concurso de lenguaje C
Se realizó una competencia para generar grandes números. No, la programación para una máquina de Turing sigue siendo demasiado cruel, por lo que C se usó para una máquina infinita abstracta con sizeof (int) = infinity. También podría usar malloc (), y la cantidad de memoria, como la pila, es ilimitada. Solo la longitud del programa era limitada: el programa debía caber en 512 bytes (excluyendo espacios), pero se permitía el uso de un preprocesador (#define).
Los resultados se publican en
el sitio web de matemáticas . Al mismo tiempo, verifique el diseño del sitio de un verdadero matemático. Los resultados están
aquí . Aquí está el texto del programa, que ocupó el segundo lugar, dando el número sobre
f w w ( 10 500 )
typedef int J; JP(J x,J y) { return x+y ? x%2 + y%2*2 + P(x/2,y/2)*4 : 0 ;} JH(J z) { return z ? z%2 + 2*H(z/4) : 0 ;} JI(J f,J e,J r){ return f ? P(P(f,e),r) : r ;} JM(J x,J e) { return x ? I(x%2, M(e,0), M(x/2, e+1)) : 0 ;} JD(J,J); JE(J f,J e,J r,J b) { return e ? E(1, D(e,b), I(b-1, D(e,b), I(f-1,e,r)), b) : I(f-1,e,r) ; } JD(J x,J b) { return x ? E( H(H(x)), H(H(x)/2), H(x/2), b) : 0 ;} JF(J x,J b) { return x ? F(D(x,b+1),b+1) : b ;} JG(J x) { return F(M(x,9), 9) ;} J f(J n,J x) { return n ? f(n-1, G(x ? f(n,x-1) : n)) : G(x) ;} J g(J x) { return f(x,x) ;} J h(J n,J x) { return n ? h(n-1, g(x ? h(n,x-1) : n)) : g(x) ;} J main(void) { return h(g(9),9) ;}
El texto del programa ganador es más largo, solo quería mostrar dónde comienza:
#define R { return #define PP ( #define LL ( #define TS (v, y, c, #define C ), #define X x) #define F );}
Pero incluso al organizador del concurso le resultó difícil evaluar qué tan grande resultó el número (escrito
muy grande )
Castores ocupados
Bien, lo suficiente como para lidiar con números pequeños, hagamos los grandes. Imagine que se ha organizado un concurso universal para escribir un programa para generar el mayor número. Como el número de programas no supera los 512 caracteres, por supuesto, siempre hay un ganador absoluto. Vamos a designarlo como BB (512) -
función de castor ocupado .
Está claro que BB (1024) >> BB (512). Pero, ¿qué tan rápido crece la función BB? Resulta que está creciendo más rápido que todo lo que conocimos. La función BB en sí misma es algorítmicamente insoluble; no se puede calcular en una computadora. Pero a medida que aumenta la duración del programa válido, podemos implementar más y más ideas nuevas. Entonces BB crece más rápido que cualquier función algorítmicamente decidible.
PIE GRANDE
Bien, lo suficiente como para lidiar con números pequeños, hagamos los grandes. Ah, ¿ya dije eso? Sería genial ejecutar BB (BB (n)). Pero dado que BB no es computable, existen dificultades técnicas con esto (tal función es computable en máquinas Turing con oráculos, para no confundir los oráculos con Oracle DBMS).
Pero puede hacerlo más fácilmente, en lugar de un
programa, considere una
fórmula con cuantificadores de longitud n. Una fórmula cuantificadora no importa si algo es computable o no. Por lo tanto, al menos puede tomar la función BB (1,000,000,000) y aplicarla a usted BB (BB (BB (1,000,000))) veces. Y esto es solo lo que primero vino a mi mente.
El número más grande que puede denotarse mediante una fórmula de como máximo n caracteres se denota por FOOT (n).
P I E G R A N D E = P I E 10 ( 10 100 )
PS
Para el próximo artículo me gustaría entender en qué enfocarme, participe en la encuesta por favor