🥪 🔹 🍱 Disminución del tamaño de la muestra de datos experimentales sin pérdida de información. 🔙 ☘️ 🧘🏼

¿Cuál es el problema de los histogramas de datos experimentales?

La base de la gestión de la calidad del producto de cualquier empresa industrial es la recopilación de datos experimentales con su posterior procesamiento.

El procesamiento inicial de los resultados experimentales implica comparar las hipótesis sobre la ley de la distribución de datos, que describe, con el error más pequeño, una variable aleatoria sobre la muestra observada.

Para esto, la muestra se presenta en forma de histograma que consiste en

k

$k$ columnas construidas a intervalos de longitud

d

$d$ .

La identificación de la forma de la distribución de los resultados de medición también requiere una serie de problemas cuya eficacia de solución difiere para diferentes distribuciones (por ejemplo, utilizando el método de mínimos cuadrados o calculando las estimaciones de entropía).

Además, la identificación de la distribución también es necesaria porque la dispersión de todas las estimaciones (desviación estándar, exceso, curtosis, etc.) también depende de la forma de la ley de distribución.

El éxito de identificar la forma de distribución de los datos experimentales depende del tamaño de la muestra y, si es pequeño, las características de distribución están enmascaradas por la aleatoriedad de la muestra misma. En la práctica, no es posible proporcionar un tamaño de muestra grande, por ejemplo, más de 1000, por varias razones.

En tal situación, es importante distribuir los datos de la muestra de la mejor manera en los intervalos, cuando la serie de intervalos es necesaria para posteriores análisis y cálculos.

Por lo tanto, para una identificación exitosa, es necesario resolver el problema de asignar el número de intervalos k

A. Hald en el libro [1] convence ampliamente de que hay un número óptimo de intervalos de agrupación cuando la envolvente escalonada del histograma construido en estos intervalos está más cerca de la curva de distribución uniforme de la población general.

Uno de los signos prácticos de acercarse al óptimo es la desaparición de las inmersiones en el histograma, y luego la mayor k se considera cercana al óptimo, en el que el histograma aún conserva un carácter uniforme.

Obviamente, el tipo de histograma depende de la construcción de intervalos de pertenencia a una variable aleatoria, sin embargo, incluso en el caso de una partición uniforme, todavía no se dispone de un método satisfactorio para esta construcción.

La partición, que podría considerarse correcta, lleva al hecho de que el error de aproximación por la función constante por partes de la densidad de distribución supuestamente continua (histograma) será mínimo.

Las dificultades son causadas por el hecho de que la densidad estimada es desconocida; por lo tanto, el número de intervalos afecta fuertemente la forma de la distribución de frecuencia de la muestra final.

Para una longitud de muestra fija, la ampliación de los intervalos de partición conduce no solo a un refinamiento de la probabilidad empírica de entrar en ellos, sino también a una pérdida inevitable de información (tanto en el sentido general como en el sentido de la curva de distribución de densidad de probabilidad), por lo tanto, con una ampliación injustificada adicional, la distribución estudiada se suaviza demasiado. .

Una vez que ha surgido, la tarea de dividir óptimamente el rango bajo el histograma no desaparece del campo de visión de los especialistas, y hasta que aparezca la única opinión establecida sobre su solución, la tarea seguirá siendo relevante.

Elección de criterios para evaluar la calidad del histograma de datos experimentales.

El criterio de Pearson, como se sabe, requiere dividir la muestra en intervalos: en ellos se evalúa la diferencia entre el modelo adoptado y la muestra comparada.

c h i^{2} = s u m_{j = 1}^{m} f r a c (E_{j} - M_{j})^{2} M_{j}

$\ chi ^ {2} = \ sum_ {j = 1} ^ {m} \ frac {(E_ {j} -M_ {j}) ^ {2}} {M_ {j}}$

donde:

E_{j}

$E_ {j}$ - frecuencias experimentales

(n_{j})

$(n_ {j})$ ;

M_{j}

$M_ {j}$ - valores de frecuencia en la misma columna; número m de columnas de histograma.

Sin embargo, la aplicación de este criterio en el caso de intervalos de longitud constante, generalmente utilizados para construir histogramas, es ineficiente. Por lo tanto, en los trabajos sobre la efectividad del criterio de Pearson, los intervalos se consideran no con la misma longitud, sino con la misma probabilidad de acuerdo con el modelo aceptado.

En este caso, sin embargo, el número de intervalos de igual longitud y el número de intervalos de igual probabilidad difieren varias veces (con la excepción de una distribución igualmente probable), lo que permite dudar de la fiabilidad de los resultados obtenidos en [2].

Como criterio de proximidad, es aconsejable utilizar el coeficiente de entropía, que se calcula de la siguiente manera [3]:

k_{e} = f r a c d n 2 s i g m a 10^{b e t a}

$k_ {e} = \ frac {dn} {2 \ sigma} 10 ^ {\ beta}$

b e t a = - f r a c 1 n s u m_{i = 1}^{m} n_{i} l g (n_{i})

$\ beta = - \ frac {1} {n} \ sum_ {i = 1} ^ {m} {n_ {i} lg (n_ {i})}$

donde:

n_{i}

$n_ {i}$ - el número de observaciones en el intervalo i-ésimo

i = 0, . . ., m

$i = 0, ..., m$

Algoritmo para evaluar la calidad del histograma de datos experimentales utilizando el coeficiente de entropía y el módulo numpy.histogram

La sintaxis para usar el módulo es la siguiente [4]:

numpy.histogram (a, bins = m, range = None, normed = None, pesos = Ninguno, densidad = Ninguno)

Consideraremos métodos para encontrar el número óptimo m de intervalos de división de histograma implementados en el módulo numpy.histogram:

• 'auto' : clasificaciones máximas de 'sturges' y 'fd' , proporciona un buen rendimiento;
• 'fd' (Freedman Diaconis Estimator) : un evaluador confiable (resistente a las emisiones) que tiene en cuenta la variabilidad y el tamaño de los datos;
• 'doane' : una versión mejorada de la estimación de sturges que funciona con mayor precisión con conjuntos de datos con una distribución no normal;
• 'scott' es un evaluador menos confiable que tiene en cuenta la variabilidad y el tamaño de los datos;
• 'piedra' : el evaluador se basa en una verificación cruzada de la estimación del cuadrado del error, puede considerarse como una generalización de la regla de Scott;
• 'arroz' : el evaluador no tiene en cuenta la variabilidad, sino solo el tamaño de los datos, a menudo sobreestima el número de intervalos requeridos;
• 'sturges' : el método (por defecto), teniendo en cuenta solo el tamaño de los datos, es óptimo solo para datos gaussianos y subestima el número de intervalos para grandes conjuntos de datos no gaussianos;
• 'sqrt' es el estimador de raíz cuadrada para el tamaño de datos utilizado por Excel y otros programas para cálculos rápidos y fáciles de la cantidad de intervalos.

Para comenzar la descripción del algoritmo, adaptamos el módulo numpy.histogram () para calcular el coeficiente de entropía y el error de entropía:

from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#       m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#  ke=h/std (a)#    (1). return ke,h

Ahora considere las etapas principales del algoritmo:

1) Formamos una muestra de control (en adelante denominada "muestra grande") que cumple los requisitos para el error en el procesamiento de datos experimentales . A partir de una muestra grande, al eliminar todos los miembros impares, formamos una muestra más pequeña (en adelante denominada "muestra pequeña");

2) Para todos los evaluadores 'auto', 'fd', 'doane', 'scott', 'stone', 'rice', 'sturges', 'sqrt' calculamos el coeficiente de entropía ke1 y el error h1 para una muestra grande y el coeficiente de entropía ke2 y el error h2 para una muestra pequeña, así como el valor absoluto de la diferencia - abs (ke1-ke2);

3) Controlando los valores numéricos de los evaluadores al nivel de al menos cuatro intervalos, seleccionamos el evaluador que proporciona el valor mínimo de la diferencia absoluta - abs (ke1-ke2).

4) Para la decisión final sobre la elección de un evaluador, construimos en un histograma las distribuciones para las muestras grandes y pequeñas con el evaluador proporcionando el valor mínimo de abs (ke1-ke2), y en el segundo con el evaluador proporcionando el valor máximo de abs (ke1-ke2). La aparición de saltos adicionales en una pequeña muestra en el segundo histograma confirma la elección correcta del evaluador en el primero.

Considere el trabajo del algoritmo propuesto en una muestra de datos de una publicación [2]. Los datos se obtuvieron seleccionando al azar 80 espacios en blanco de 500 con la medición posterior de su masa. La pieza de trabajo debe tener una masa en los siguientes límites:

m = 17_{- 0.4}^{+ 0.6}

$m = 17 _ {- 0.4} ^ {+ 0.6}$ kg Determinamos los parámetros óptimos del histograma utilizando la siguiente lista:

Listado

 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#      m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#   ke=h/std (a)#  return ke,h a =array([17.37, 17.06, 16.96, 16.83, 17.34, 17.45, 17.60, 17.30, 17.02, 16.73, 17.08, 17.28, 17.08, 17.21, 17.29,17.47, 16.84, 17.39, 16.95, 16.92, 17.59, 17.28, 17.31, 17.25, 17.43,17.30, 17.18, 17.26, 17.19, 17.09,16.61, 17.16, 17.17, 17.06, 17.09,16.83, 17.17, 17.06, 17.59, 17.37,17.09, 16.94, 16.76, 16.98, 16.70, 17.27, 17.48, 17.21, 16.74, 17.12,17.33, 17.15, 17.56, 17.45, 17.49,16.94, 17.28, 17.09, 17.39, 17.05, 16.97, 17.16, 17.38, 17.23, 16.87,16.84, 16.94, 16.90, 17.27, 16.93,17.25, 16.85, 17.41, 17.37, 17.50,17.13, 17.16, 17.05, 16.68, 17.56 ] ) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print("     (n=80) : %s"%round(std(a),3)) print("    (n=80):%s"%round(mean(a),3)) print("     (n=40): %s"%round(std(b),3)) print("   (n=40): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n    abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title('  : %s \n    abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()

Obtenemos:

La desviación estándar para la muestra (n = 80): 0.24
La expectativa matemática para la muestra (n = 80): 17.158
La desviación estándar para la muestra (n = 40): 0.202
La expectativa matemática de la muestra (n = 40): 17.138
ke1 = 1.95, h1 = 0.467, ke2 = 1.917, h2 = 0.387, dke = 0.033, m = auto
ke1 = 1.918, h1 = 0.46, ke2 = 1.91, h2 = 0.386, dke = 0.008, m = fd
ke1 = 1.831, h1 = 0.439, ke2 = 1.917, h2 = 0.387, dke = 0.086, m = doane
ke1 = 1.918, h1 = 0.46, ke2 = 1.91, h2 = 0.386, dke = 0.008, m = scott
ke1 = 1.898, h1 = 0.455, ke2 = 1.934, h2 = 0.39, dke = 0.036, m = piedra
ke1 = 1.831, h1 = 0.439, ke2 = 1.917, h2 = 0.387, dke = 0.086, m = arroz
ke1 = 1.95, h1 = 0.467, ke2 = 1.917, h2 = 0.387, dke = 0.033, m = esturiones
ke1 = 1.831, h1 = 0.439, ke2 = 1.917, h2 = 0.387, dke = 0.086, m = sqrt

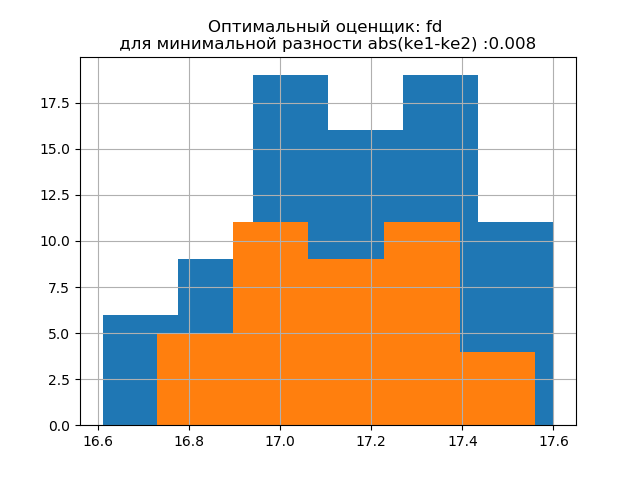
La forma de la distribución de una muestra grande es similar a la forma de la distribución de una muestra pequeña. Como se deduce del guión, 'fd' es un evaluador confiable (resistente a las emisiones) que tiene en cuenta la variabilidad y el tamaño de los datos. En este caso, el error de entropía de la muestra pequeña incluso disminuye ligeramente: h1 = 0.46, h2 = 0.386 con una ligera disminución en el coeficiente de entropía de k1 = 1.918 a k2 = 1.91.

Los patrones de distribución de muestras grandes y pequeñas difieren. Como sugiere la descripción, 'doane' es una versión mejorada del puntaje 'sturges' que funciona mejor con conjuntos de datos con una distribución no normal. En ambas muestras, el coeficiente de entropía es cercano a dos, y la distribución es cercana a la normalidad. La aparición de saltos adicionales en una muestra pequeña en este histograma, en comparación con la anterior, indica adicionalmente la elección correcta del evaluador 'fd' .

Generamos dos nuevas muestras para la distribución normal con los parámetros mu = 20, sigma = 0.5 y size = 100 usando la relación:

 a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)])

El método desarrollado es aplicable a la muestra obtenida utilizando el siguiente programa:

Listado

 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#      m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#   ke=h/std (a)#  return ke,h #a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)]) a=array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945,20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print("     (n=100):%s"%round(std(a),3)) print("    (n=100):%s"%round(mean(a),3)) print("     (n=50):%s"%round(std(b),3)) print("   (n=50): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n    abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title('  : %s \n    abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()

Obtenemos:
La desviación estándar para la muestra (n = 100): 0.524
La expectativa matemática para la muestra (n = 100): 19.992
La desviación estándar para la muestra (n = 50): 0.462
La expectativa matemática de la muestra (n = 50): 20.002
ke1 = 1.979, h1 = 1.037, ke2 = 2.004, h2 = 0.926, dke = 0.025, m = auto
ke1 = 1.979, h1 = 1.037, ke2 = 1.915, h2 = 0.885, dke = 0.064, m = fd
ke1 = 1.979, h1 = 1.037, ke2 = 1.804, h2 = 0.834, dke = 0.175, m = doane
ke1 = 1.943, h1 = 1.018, ke2 = 1.934, h2 = 0.894, dke = 0.009, m = scott
ke1 = 1.943, h1 = 1.018, ke2 = 1.804, h2 = 0.834, dke = 0.139, m = piedra
ke1 = 1.946, h1 = 1.02, ke2 = 1.804, h2 = 0.834, dke = 0.142, m = arroz
ke1 = 1.979, h1 = 1.037, ke2 = 2.004, h2 = 0.926, dke = 0.025, m = esturiones
ke1 = 1.946, h1 = 1.02, ke2 = 1.804, h2 = 0.834, dke = 0.142, m = sqrt

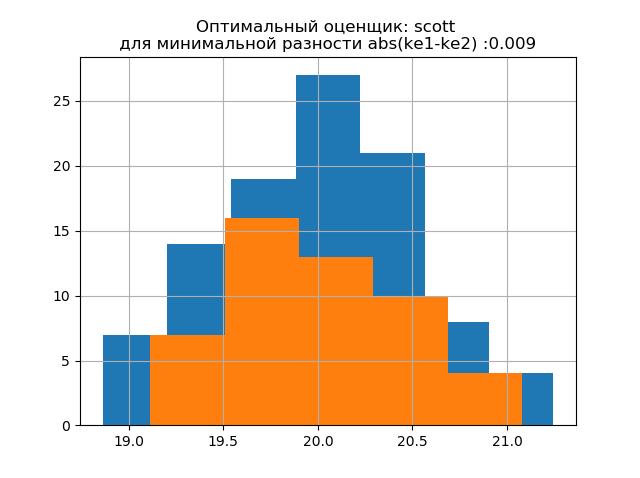
La forma de distribución de una muestra grande es similar a la forma de distribución de una muestra pequeña. Como se desprende de la descripción, 'scott' es un evaluador menos confiable que tiene en cuenta la variabilidad y el tamaño de los datos. En este caso, el error de entropía de una muestra pequeña incluso disminuye ligeramente: h1 = 1.018 y h2 = 0.894 con una ligera disminución en el coeficiente de entropía de k1 = 1.943 a k2 = 1.934. . Cabe señalar que para la nueva muestra tenemos la misma tendencia a cambiar los parámetros que en el ejemplo anterior.

Los patrones de distribución de muestras grandes y pequeñas difieren. Como se desprende de la descripción, 'doane' es una versión mejorada de la estimación de 'sturges' , que funciona con mayor precisión con conjuntos de datos con una distribución no normal. En ambas muestras, la distribución es normal. La aparición de saltos adicionales en una pequeña muestra en este histograma en comparación con el anterior también indica la elección correcta del evaluador 'scott' .

El uso de anti-aliasing para el análisis comparativo de histogramas.

El suavizado de los histogramas creados en las muestras grandes y pequeñas le permite determinar con mayor precisión su identidad desde el punto de vista de preservar la información contenida en una muestra más grande. Imagine los dos últimos histogramas como funciones de suavizado:

Listado

 from numpy import* from scipy.interpolate import UnivariateSpline from matplotlib import pyplot as plt a =array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945, 20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] plt.title('    \n  abs(ke1-ke2)' ,size=12) z=histogram(a, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=100') z=histogram(b, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=50') plt.legend(loc='best') plt.grid() plt.show() plt.title('    \n  abs(ke1-ke2)' ,size=12) z=histogram(a, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=100') z=histogram(b, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=50') plt.legend(loc='best') plt.grid() plt.show()

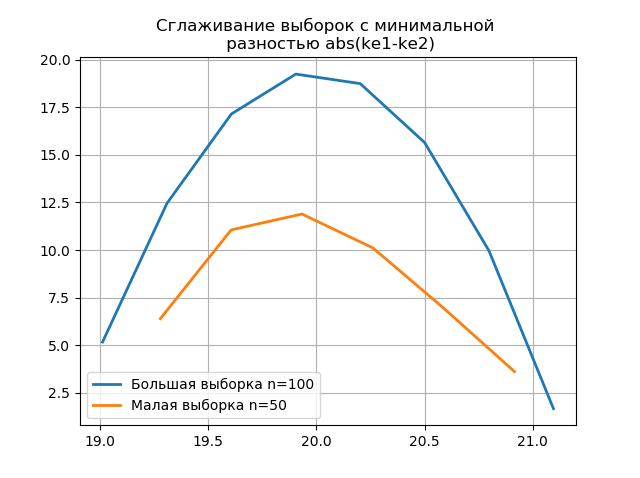
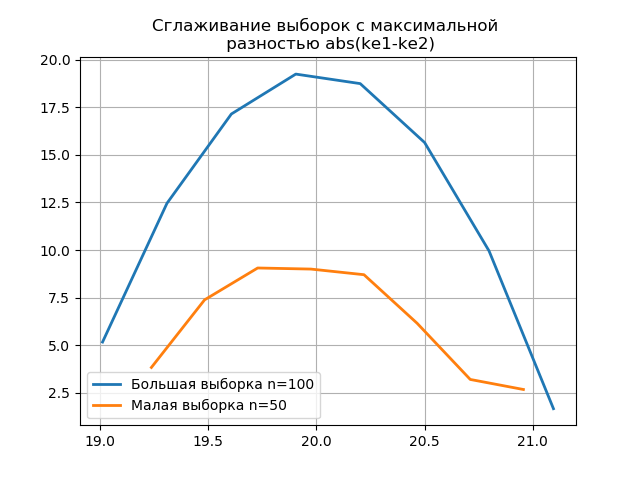
La aparición de saltos adicionales en una pequeña muestra en el gráfico de un histograma suavizado en comparación con el anterior también indica la elección correcta del evaluador scott .

Conclusiones

Los cálculos presentados en el artículo en el rango de pequeñas muestras comunes en la producción confirmaron la eficiencia del uso del coeficiente de entropía como criterio para mantener el contenido de la información de la muestra mientras se reduce su volumen . Se considera la técnica de usar la última versión del módulo numpy.histogram con evaluadores integrados: 'auto', 'fd', 'doane', 'scott', 'stone', 'rice', 'sturges', 'sqrt', que son suficientes para la optimización Análisis de datos experimentales sobre estimaciones de intervalos.

Referencias

1. Hald A. Estadística matemática con aplicaciones técnicas. - Moscú: editorial. lit., 1956
2. Kalmykov V.V., Antonyuk F.I., Zenkin N.V.
Determinación del número óptimo de clases de agrupación de datos experimentales para estimaciones de intervalo // South Siberian Scientific Bulletin. - 2014. - No. 3. - P. 56-58.
3. Novitsky P. V. El concepto del valor de entropía del error // Técnica de medición. - 1966. - No. 7. —S. 11-14.
4.numpy.histogram - NumPy v1.16 Manual

Disminución del tamaño de la muestra de datos experimentales sin pérdida de información.

¿Cuál es el problema de los histogramas de datos experimentales?

Elección de criterios para evaluar la calidad del histograma de datos experimentales.

Algoritmo para evaluar la calidad del histograma de datos experimentales utilizando el coeficiente de entropía y el módulo numpy.histogram

El uso de anti-aliasing para el análisis comparativo de histogramas.

Conclusiones

Referencias

More articles: