Geekly articles weekly

Mónadas desde el punto de vista de los programadores (y un poco de teoría de categorías)

Introduccion


¿Cómo descubrir que una persona entendió lo que son las mónadas? Él mismo le informará sobre esto en los primeros 5 minutos de comunicación y ciertamente tratará de explicarlo. También escribirá un texto al respecto y, si es posible, lo publicará en algún lugar, para que todos los demás también entiendan qué son las mónadas.


Entre los programadores funcionales, especialmente en Haskell, las mónadas se han convertido en un meme local. A menudo se intenta explicar, comenzando por casos especiales e inmediatamente dando ejemplos de uso. Debido a esto, el oyente puede no comprender la esencia principal del concepto, y las mónadas seguirán siendo magia negra, o simplemente un medio para aplastar los efectos secundarios en lenguajes puramente funcionales.


Primero hablaré sobre los conceptos básicos de la teoría de categorías, y luego, desde un punto de vista práctico, abordaremos la definición de una mónada y veremos que, de hecho, muchos programadores usan esta poderosa abstracción en una de sus manifestaciones.


Mi presentación se basa en gran medida en el libro de Bartosz Milewski, Category Theory for Programmers, que fue creado como una serie de publicaciones de blog , está disponible en PDF y recientemente se publicó en papel.


Los ejemplos se proporcionan en Haskell, se supone que el lector está familiarizado con la sintaxis y los conceptos básicos del lenguaje. En el libro mencionado hay ejemplos en C ++, puede comparar la pureza y la comprensión del código.



Categorias


Definición


Las categorías en sí son construcciones muy simples. Una categoría es una colección de objetos y morfismos entre ellos. Los morfismos pueden considerarse flechas unidireccionales que conectan objetos. En el caso general, no se sabe nada sobre la esencia de los objetos mismos. La teoría de categorías no funciona con objetos, sino con morfismos, o más bien, con su composición .


Se utiliza la siguiente notación:


  • Ob C - objetos de la categoría C ;
  • Hom C (A, B) - morfismos de A a B;
  • g ∘ f es la composición de los morfismos f y g.

Al definir una categoría, los morfismos están sujetos a restricciones adicionales:


  1. Para un par de morfismos f y g, si f es un morfismo de A a B (f ∈ Hom (A, B)), g es un morfismo de B a C (g ∈ Hom (B, C)), entonces existe una composición g ∘ f es un morfismo de A a C (g ∘ f ∈ Hom (A, C)).
  2. Para cada objeto, se da una identidad de morfismo de identidad A ∈ Hom (A, A).

Hay dos propiedades importantes que cualquier categoría debe satisfacer (axiomas de la teoría de categorías):


  1. La asociatividad de la composición: h ∘ (g ∘ f) = (h ∘ g) ∘ f;
  2. Composición con el morfismo de identidad: si f ∈ Hom (A, B), entonces f ∘ id A = id B ∘ f = f.

Las categorías se visualizan de manera muy fácil y natural como gráficos dirigidos. En principio, cualquier gráfico orientado puede extenderse a una categoría agregando composiciones de morfismos y morfismos idénticos, si es necesario.



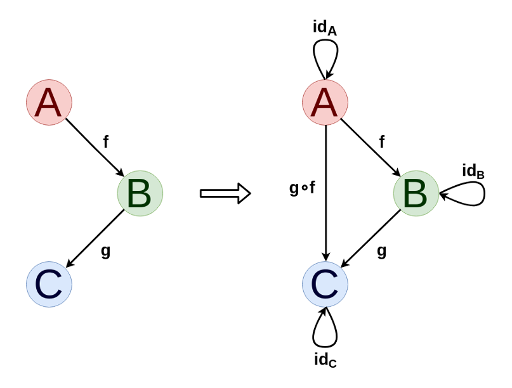
Para cualquier categoría, puede definir una categoría dual (denotada por C op , en la que los morfismos se obtienen girando las flechas de la categoría original, y los objetos son los mismos. Esto nos permite formular enunciados y teoremas duales, cuya verdad no cambia cuando las flechas se invierten.


Los objetos y los morfismos no necesariamente forman conjuntos (en el sentido clásico, de la teoría de conjuntos), por lo tanto, en el caso general, se usa la frase "clase de objetos". Las categorías en las que las clases de objetos y morfismos siguen siendo conjuntos se denominan categorías pequeñas . Además, trabajaremos solo con ellos.


Tipos y funciones


, Haskell, — . , Int Bool — , Int -> Bool — .


id, :


id :: a -> a
id x = x

— , Haskell :


f :: a -> b
g :: b -> c
g . f :: a -> c
(g . f) x = g (f x)

, , — , Set. , — , : . bottom, _|_. , , , bottom. Haskell, , Hask. , Set. , , : HomC(A, B) ∈ C. , a -> b — Haskell.


.


Void, ( ). absurd, , , Void, :


absurd :: Void -> a

Unit, — , (). unit , :


unit :: a -> Unit
unit _ = ()

— Bool:


data Bool = True | False

, Void, Unit Bool.


Void , absurd, Bool, Unit. , Void, , .


Bool -> Unit , unit, . Unit -> Bool . (), True, False. , Unit Bool:


true, false :: a -> Bool
true _ = True
false _ = False

Bool Bool — , 4 ( n — 22n): id, true false, , not:


not :: Bool -> Bool
not True = False
not False = True

, :



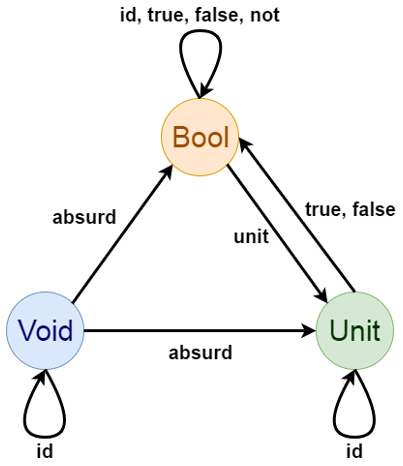
Haskell- .



— . , C D, F . -, C D. a — C, F a — D, . -, : f :: a -> b C F f :: F a -> F b D.



, " " :


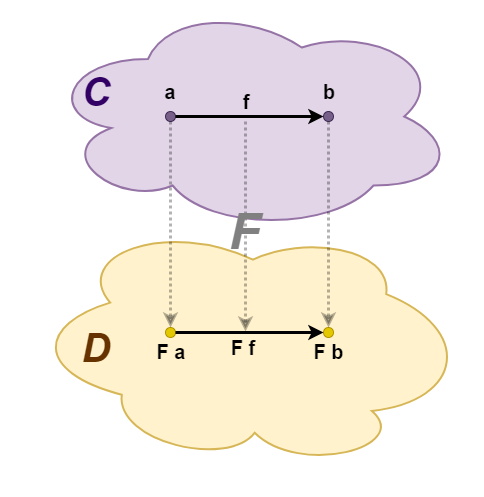
  1. h = g ∘ f, F h = F g ∘ F f.
  2. ida — a, F ida = idF a — F a.

, "" : , , . , , () . , .


. , F :: C -> D G :: D -> E G . F :: C -> E. , , , , . IdC, IdD IdE. , , .



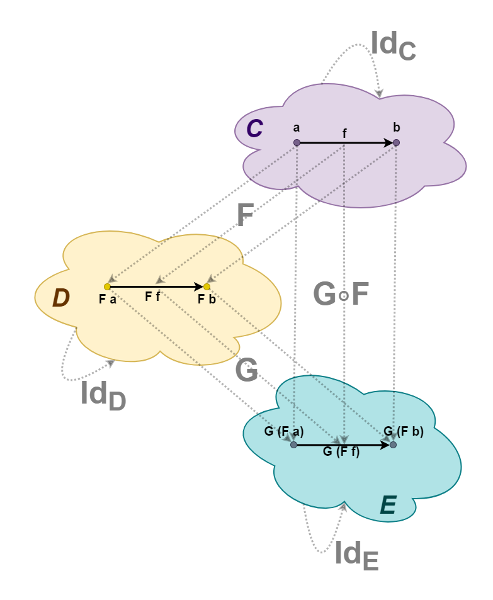
, , -, — (). , Cat ( ).


Haskell . , , - , .


Maybe , a Maybe a ( Maybe !):


data Maybe a = Nothing | Just a

, f :: a -> b F f :: Maybe a -> Maybe b. fmap. , ( ):


--          f                F f
--      /------\    /------------------\
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)

, Maybe — . , , Functor. fmap, , ( — ):


class Functor f where
  fmap :: (a -> b) -> f a -> f b

— , , fmap . f a -> f b, , .



, , , .. , . : , - .


. , . , , — Haskell.


: upCase, , toWords, . toUpper words:


upCase :: String -> String
upCase = map toUpper

toWords :: String -> [String]
toWords = words

:


processString :: String -> [String]
processString = toWords . upCase

, . , processString "upCase toWords".


— , . -, , , -, , .


, a , .


newtype Writer a = Writer (a, String)

, Writer — , fmap:


instance Functor Writer where
  fmap f (Writer (x, s)) = Writer (f x, s)

upCase toWords , , "" Writer:


upCase :: String -> Writer String
upCase s = Writer (map toUpper s, "upCase ")

toWords :: String -> Writer [String]
toWords s = Writer (words s, "toWords ")

, , - . , b , , c c , :


compose :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
compose f g = \x -> let Writer (y, s1) = f x
                        Writer (z, s2) = g y
                    in Writer (z, s1 ++ s2)

processString :


processString :: String -> [String]
processString = compose upCase toWords

. () a -> b a -> Writer b , a b. , .. a -> Writer a:


writerId :: a -> Writer a
writerId x = Writer (x, "")

, , Hask. , a b a -> b, a -> m b, .. "" - m. (embellished). m, Writer — .


C m. K, , C, .. ObK = ObC. a -> b K a -> m b C: HomK(a, b) = HomC(a, m b). , , K — C.


, , , . , m — . Haskell ( Hask):


class Monad m where
  --    
  (>=>)  :: (a -> m b) -> (b -> m c) -> (a -> m c)
  --  
  return :: a -> m a

>=>, "fish", : . , , — , , , . Writer — , compose — >=>, writerId — return.


>=> . , -. a, f, , , bind:


f >=> g = \a -> let mb = f a
                in (bind mb g)
  where
    bind :: m b -> (b -> m c) -> m c

bind b " " m , b m c. >=>. : m b -> (b -> m c) -> m c. , . "" Haskell >>=, bind, return:


class Monad m where
  (>>=)  :: m a -> (a -> m b) -> m b
  return :: a -> m a

, - b -> m c b, m b. , m, fmap, (a -> m b) -> m a -> m (m b). >>= m (m b) m b, "" , . join:


ma >>= g = join (fmap g ma)
  where
    join :: m (m a) -> m a

, Writer :


join :: Writer (Writer a) -> Writer a
join (Writer ((Writer (x, s2)), s1)) = Writer (x, s1 ++ s2)

Monad:


class Functor m => Monad m where
  join   :: m (m a) -> m a
  return :: a -> m a

, m . , fmap >>=:


fmap :: (a -> b) -> m a -> m b
fmap f ma = ma >>= (\a -> return (f a))


, "" .



(.. , ) .


(a -> [b]) -> (b -> [c]) -> (a -> [c]). :


(>=>) :: (a -> [b]) -> (b -> [c]) -> (a -> [c])
f >=> g = \x -> concat (map g (f x))

. a, , — f [b]. , b — g : map g (f x) :: [[c]]. , .


>>= :


(>>=) :: [a] -> (a -> [b]) -> [b]
xs >>= f = concat (map f xs)

return :: a -> [a]. :


return :: a -> [a]
return x = [x]

Monad:


instance Monad [] where
  xs >>= f = concat (map f xs)
  return x = [x]

, . , , . , — , ..



, , - .


, , Maybe. Just, — Nothing. , , :


(>=>) :: (a -> Maybe b) -> (b -> Maybe c) -> (a -> Maybe c)
f >=> g = \x -> case f x of
                  Just y  -> g y
                  Nothing -> Nothing

Monad Maybe:


instance Monad Maybe where
  (Just x) >>= f = f x
  Nothing  >>= f = Nothing
  return x = Just x

, . , - , , - . Either String a, : , . :


data Either a b = Left a | Right b

, . . :


type WithException a = Either String a

Maybe:


(>=>) :: (a -> WithException b) -> (b -> WithException c) -> (a -> WithException c)
f >=> g = \x -> case f x of
                  Right y -> g y
                  err     -> err

Monad :


instance Monad WithException where
  (Right x) >>= f = f x
  err >>= f = err
  return x = Right x


, , write-only , . a -> b , , . , , ( , ):


a -> s -> (b, s)

:


newtype State s a = State (s -> (a, s))

s , State s . runState:


runState :: State s a -> s -> (a, s)
runState (State f) s = f s

Functor:


instance Functor (State s) where
  fmap f state = State st'
    where
     st' prevState = let (a, newState) = runState state prevState
                     in (f a, newState)

, a b, , a -> State s b, State s — . , :


(>=>) :: (a -> State s b) -> (b -> State s c) -> (a -> State s c)
f >=> g = \x -> State (\s -> let (y, s') = runState (f x) s
                             in runState (g y) s')

Monad. , return, , -:


instance Monad (State s) where
  stateA >>= f = State (\s -> let (a, s') = runState stateA s
                              in runState (f a) s')
  return a = State (\s -> (a, s))

, . , Unit s , Unit -> State s s:


get :: Unit -> State s s
get _ = State (\s -> (s, s))

, Unit . , .


, , . , , , s Unit, s -> State s Unit:


put :: s -> State s Unit
put s = State (\_ -> ((), s))

, , /. , " " RealWorld, . RealWorld - , (, ). :


type IO a = State RealWorld a

IO — , Haskell, "". , . , , , -, .

Source: https://habr.com/ru/post/445488/

More articles:


All Articles