㊗️ 🧚🏻 👨🏻 Estados cuánticos neuronales: representación de una función de onda por una red neuronal 🤴🏻 🚋 🚛

En este artículo, consideraremos la aplicación inusual de las redes neuronales en general y las máquinas de Boltzmann limitadas en particular para resolver dos problemas complejos de la mecánica cuántica: encontrar la energía del estado fundamental y aproximar la función de onda de un sistema de muchos cuerpos.

Podemos decir que esta es una narración gratuita y simplificada de un artículo [2], publicado en Science en 2017 y algunos trabajos posteriores. No encontré exposiciones científicas populares de este trabajo en ruso (y solo esta de las versiones en inglés), aunque me pareció muy interesante.

Conceptos mínimos esenciales de la mecánica cuántica y el aprendizaje profundo.

Quiero señalar de inmediato que estas definiciones están extremadamente simplificadas . Los traigo para aquellos para quienes el problema descrito es un bosque oscuro.

Un estado es simplemente un conjunto de cantidades físicas que describen un sistema. Por ejemplo, para un electrón que vuela en el espacio serán sus coordenadas y su momento, y para una red cristalina será un conjunto de espines de átomos ubicados en sus nodos.

La función de onda del sistema es una función compleja del estado del sistema. Cierto cuadro negro que toma una entrada, por ejemplo, un conjunto de giros, pero devuelve un número complejo. La propiedad principal de la función de onda que es importante para nosotros es que su cuadrado es igual a la probabilidad de este estado:

P s i (s) P s i (s)^{*} = P (s)

$\ Psi (s) \ Psi (s) ^ * = P (s)$

Es lógico que el cuadrado de la función de onda se normalice a la unidad (y este es también uno de los problemas importantes).

Espacio de Hilbert - en nuestro caso, tal definición es suficiente - el espacio de todos los estados posibles del sistema. Por ejemplo, para un sistema de 40 giros que puede tomar los valores +1 o -1, el espacio de Hilbert es todo

2^{40}

$2 ^ {40}$ posibles condiciones. Para coordenadas que pueden tomar valores

[- i n f t y, + i n f t y]

$[- \ infty, + \ infty]$ , la dimensión del espacio de Hilbert es infinita. La enorme dimensión del espacio de Hilbert para cualquier sistema real es el problema principal que no permite resolver ecuaciones analíticamente: en el proceso habrá integrales / sumas sobre todo el espacio de Hilbert que no pueden calcularse "de frente". Un dato curioso: durante toda la vida del Universo puedes conocer solo una pequeña parte de todos los estados posibles incluidos en el espacio de Hilbert. Esto está muy bien ilustrado por una imagen de un artículo sobre Tensor Networks [1], que representa esquemáticamente todo el espacio de Hilbert y aquellos estados que se pueden cumplir después de un polinomio a partir de la característica de la complejidad del espacio (número de cuerpos, partículas, espines, etc.)

Una máquina de Boltzmann limitada : si es difícil de explicar, es un modelo probabilístico gráfico no dirigido, cuya limitación es la independencia condicional de las probabilidades de los nodos de una capa de los nodos de la misma capa. Si es de una manera simple, entonces esta es una red neuronal con una entrada y una capa oculta. Los valores de salida de las neuronas en la capa oculta pueden ser 0 o 1. La diferencia con la red neuronal habitual es que las salidas de las neuronas de la capa oculta son variables aleatorias seleccionadas con una probabilidad igual al valor de la función de activación:

P_{i} (1) = s i g m a (b_{i} + s u m_{j} W_{i j} s_{j})

$P_i (1) = \ sigma (b_i + \ sum_jW_ {ij} s_j)$

donde

s i g m a

$\ sigma$ - función de activación sigmoidea ,

b_{i}

$b_i$ - compensación para la i-ésima neurona,

W

$W$ - el peso de la red neuronal,

s_{j}

$s_j$ - capa visible. Las máquinas de Boltzmann limitadas pertenecen a los llamados "modelos de energía", ya que podemos expresar la probabilidad de un estado particular de una máquina utilizando la energía de esta máquina:

E (v, h) = - a^{T} v - b^{T} h - v^{T} W h

$E (v, h) = -a ^ Tv - b ^ Th - v ^ TWh$

donde v y h son las capas visibles y ocultas, a y b son los desplazamientos de las capas visibles y ocultas, W son los pesos. Entonces la probabilidad del estado es representable en la forma:

P (v, h) = f r a c 1 Z e^{- E (v, h)}

$P (v, h) = \ frac {1} {Z} e ^ {- E (v, h)}$

donde Z es el término de normalización, también llamado suma estadística (es necesario para que la probabilidad total sea igual a la unidad).

Introduccion

Hoy en día, existe una opinión entre los especialistas en aprendizaje profundo que limita
Las máquinas de Boltzmann (en adelante, OMB) son un concepto obsoleto que prácticamente no es aplicable en tareas reales. Sin embargo, en 2017, apareció un artículo [2] en Science que mostraba el uso muy eficiente de OMB para problemas de mecánica cuántica.

Los autores notaron dos hechos importantes que pueden parecer obvios, pero nunca antes se le habían ocurrido a nadie:

OMB es una red neuronal que, según el teorema universal de Tsybenko , teóricamente puede aproximar cualquier función con una precisión arbitrariamente alta (todavía hay muchas restricciones, pero puede omitirlas).
OMB es un sistema cuya probabilidad de cada estado es una función de la entrada (capa visible), pesos y desplazamientos de la red neuronal.

Bueno y más allá, los autores dijeron: dejemos que nuestro sistema sea completamente descrito por la función de onda, que es la raíz de la energía OMB, y las entradas OMB son las características de nuestro estado del sistema (coordenadas, giros, etc.):

P s i (s) = f r a c 1 Z s q r t e^{E (s, h)}

$\ Psi (s) = \ frac {1} {Z} \ sqrt {e ^ {E (s, h)}}$

donde s son características del estado (por ejemplo, giros), h son las salidas de la capa oculta de OMB, E es la energía de OMB, Z es la constante de normalización (suma estadística).

Eso es todo, el artículo en Science está listo, solo quedan algunos pequeños detalles. Por ejemplo, es necesario resolver el problema de la función de partición no computable debido al gran tamaño del espacio de Hilbert. Y el teorema de Tsybenko nos dice que una red neuronal puede aproximarse a cualquier función, pero no dice en absoluto cómo encontrar un conjunto adecuado de pesos y compensaciones de red para esto. Bueno, y como siempre, la diversión comienza aquí.

Entrenamiento modelo

Ahora hay bastantes modificaciones del enfoque original, pero solo consideraré el enfoque del artículo original [2].

Desafío

En nuestro caso, la tarea de entrenamiento será la siguiente: encontrar una aproximación de la función de onda que haga más probable el estado con energía mínima. Esto es intuitivamente claro: la función de onda nos da la probabilidad de un estado, el valor propio del Hamiltoniano (el operador de energía, o incluso más simple, energía; en el marco de este artículo, esta comprensión es suficiente) para que la función de onda sea energía. Todo es simple

En realidad, nos esforzaremos por optimizar otra cantidad, la llamada energía local, que siempre es mayor o igual que la energía del estado fundamental:

E_{l o c} (s i g m a) = R e s u m_{s i g m a s i g m a^{'}} H_{s i g m a s i g m a^{'}} f r a c P s i (s i g m a^{'}) P s i (s i g m a)

$E_ {loc} (\ sigma) = Re \ sum _ {\ sigma \ sigma '} H _ {\ sigma \ sigma'} \ frac {\ Psi (\ sigma ')} {\ Psi (\ sigma)}$

aqui

s i g m a

$\ sigma$ Es nuestra condición

s i g m a^{'}

$\ sigma '$ - todos los estados posibles del espacio de Hilbert (en realidad consideraremos un valor más aproximado),

H_{s i g m a s i g m a^{'}}

$H _ {\ sigma \ sigma '}$ Es el elemento matriz del hamiltoniano. Depende mucho del Hamiltoniano específico, por ejemplo, para el modelo Ising, esto es solo

f (s i g m a)

$f (\ sigma)$ si

s i g m a = s i g m a^{'}

$\ sigma = \ sigma '$ y

- c o n s t

$-const$ en todos los demás casos. No te detengas aquí ahora; Es importante que estos elementos se puedan encontrar para varios hamiltonianos populares.

Proceso de optimización

Muestreo

Una parte importante del enfoque del artículo original fue el proceso de muestreo. Se utilizó una variación modificada del algoritmo Metropolis-Hastings . La conclusión es:

Partimos de un estado aleatorio.
Cambiamos el signo de un giro seleccionado al azar al opuesto (para las coordenadas hay otras modificaciones, pero también existen).
Con probabilidad igual a $P (\ sigma '| \ sigma) = \ Big | {\ frac {\ Psi (\ sigma')} {\ Psi (\ sigma)} \ Big | ^ 2$ , muévete a un nuevo estado.
Repite N veces.

Como resultado, obtenemos un conjunto de estados aleatorios seleccionados de acuerdo con la distribución que nos da nuestra función de onda. Puede calcular los valores de energía en cada estado y la expectativa matemática de energía

m a t h b b E (E_{l o c})

$\ mathbb {E} (E_ {loc})$ .

Se puede demostrar que la estimación del gradiente de energía (más precisamente, el valor esperado del Hamiltoniano) es igual a:

G_{k} (x) = 2 * (E_{l o c} (x) - m a t h b b E (E_{l o c})) * D_{k}^{*} (x)

$G_k (x) = 2 * (E_ {loc} (x) - \ mathbb {E} (E_ {loc})) * D ^ * _ k (x)$

Conclusión

Esto es de una conferencia dada por G. Carleo en 2017 para la Escuela Avanzada de Ciencia Cuántica y Tecnología Cuántica. Hay entradas en Youtube.

Denotar:

D_{k}^{*} (x) = f r a c p a r t i a l_{p_{k}} P s i (x) P s i (x)

$D ^ * _ k (x) = \ frac {\ partial_ {p_k} \ Psi (x)} {\ Psi (x)}$

Entonces:

p a r t i a l_{p_{k}} m a t h b b E (H) =

$\ partial_ {p_k} \ mathbb {E} (H) =$

p a r t i a l f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} =

$\ partial \ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} D_{k} (x^{'}) P s i (x^{'}) s u m_{x} | P s i (x) |^{2} + f r a c s u m_{x x^{'}} P s i^{*} (x) D_{k}^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} D_k (x ') \ Psi (x')} {\ sum_x | \ Psi (x) | ^ 2} + \ frac {\ sum_ {xx '} \ Psi ^ * (x) D_k ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} -$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) - D_{k}^{*} (x)) s u m_{x} | P s i (x) |^{2} =

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) - D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} f r a c P s i^{*} (x) P s i^{*} (x^{'}) H_{x x^{'}} D_{k} (x^{'}) | P s i (x^{'}) |^{2} + s u m_{x x^{'}} | P s i (x) |^{2} H_{x x^{'}} D_{k}^{*} (x^{'}) f r a c P s i (x^{'}) P s i (x) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ frac {\ Psi ^ * (x)} {\ Psi ^ * (x')} H_ {xx '} D_k (x') | \ Psi (x ') | ^ 2 + \ sum_ {xx '} | \ Psi (x) | ^ 2H_ {xx'} D ^ * _ k (x ') \ frac {\ Psi (x')} {\ Psi (x)}} {\ sum_x | \ Psi (x) | ^ 2} -$

m a t h b b E (H) f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) + D_{k}^{*} (x)) s u m_{x} | P s i (x) |^{2} a p r o x

$\ mathbb {E} (H) \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) + D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2 } \ aprox$

m a t h b b E (E_{l o c} D_{k}^{*}) - m a t h b b E (E_{l o c}) m a t h b b E (D_{k}^{*}) + C

$\ mathbb {E} (E_ {loc} D ^ * _ k) - \ mathbb {E} (E_ {loc}) \ mathbb {E} (D ^ * _ k) + C$

Luego solo resolvemos el problema de optimización:

Demostramos estados de nuestro OMB.
Calculamos la energía de cada estado.
Estima el gradiente.
Actualizamos el peso de OMB.

Como resultado, el gradiente de energía tiende a cero, el valor de la energía disminuye, al igual que el número de nuevos estados únicos en el proceso Metropolis-Hastings, porque al tomar muestras de la función de onda verdadera casi siempre obtendremos el estado fundamental. Intuitivamente, esto parece lógico.

En el trabajo original, para sistemas pequeños, se obtuvieron los valores de la energía del estado fundamental, muy cerca de los valores exactos obtenidos analíticamente. Se realizó una comparación con los enfoques bien conocidos para encontrar la energía del estado fundamental, y NQS ganó, especialmente teniendo en cuenta la complejidad computacional relativamente baja de NQS en comparación con los métodos conocidos.

NetKet - una biblioteca desde el enfoque de "inventores"

Uno de los autores del artículo original [2] con su equipo desarrolló la excelente biblioteca NetKet [3], que contiene un núcleo C muy bien optimizado (en mi opinión), así como la API de Python, que funciona con abstracciones de alto nivel.

La biblioteca se puede instalar a través de pip. Los usuarios de Windows 10 deberán usar Linux Subsystem para Windows.

Consideremos trabajar con la biblioteca como un ejemplo de una cadena de 40 giros tomando los valores + -1 / 2. Consideraremos el modelo de Heisenberg, que tiene en cuenta las interacciones vecinas.

NetKet tiene una excelente documentación que le permite descubrir rápidamente qué y cómo hacer. Hay muchos modelos incorporados (respaldos, bosones, modelos Ising, Heisenberg, etc.), y la capacidad de describir completamente el modelo usted mismo.

Descripción del conteo

Todos los modelos se presentan en gráficos. Para nuestra cadena, el modelo Hypercube incorporado con una dimensión y condiciones de contorno periódicas es adecuado:

import netket as nk graph = nk.graph.Hypercube(length=40, n_dim=1, pbc=True)

Descripción del espacio de Hilbert

Nuestro espacio de Hilbert es muy simple: todos los giros pueden tomar valores ya sea +1/2 o -1/2. Para este caso, el modelo incorporado para giros es adecuado:

 hilbert = nk.hilbert.Spin(graph=graph, s=0.5)

Descripción del hamiltoniano

Como ya escribí, en nuestro caso, el hamiltoniano es el hamiltoniano de Heisenberg para el que hay un operador incorporado:

 hamiltonian = nk.operator.Heisenberg(hilbert=hilbert)

Descripción de RBM

En NetKet, puede usar una implementación RBM ya preparada para giros, este es solo nuestro caso. Pero en general hay muchos autos, puedes probar diferentes.

 nk.machine.RbmSpin(hilbert=hilbert, alpha=4) machine.init_random_parameters(seed=42, sigma=0.01)

Aquí alfa es la densidad de las neuronas en la capa oculta. Para 40 neuronas visibles y alfa 4, habrá 160 de ellas. Hay otra forma de indicar directamente por número. El segundo comando inicializa pesos al azar de

N (0, s i g m a)

$N (0, \ sigma)$ . En nuestro caso, sigma es 0.01.

Samler

Una muestra es un objeto que nos devolverá una muestra de nuestra distribución, que viene dada por la función de onda en el espacio de Hilbert. Utilizaremos el algoritmo Metropolis-Hastings descrito anteriormente, modificado para nuestra tarea:

 sampler = nk.sampler.MetropolisExchangePt( machine=machine, graph=graph, d_max=1, n_replicas=12 )

Para ser precisos, el muestreador es un algoritmo más complicado que el que describí anteriormente. Aquí verificamos simultáneamente hasta 12 opciones en paralelo para seleccionar el siguiente punto. Pero el principio, en general, es el mismo.

Optimizador

Esto describe el optimizador que se usará para actualizar los pesos del modelo. Basado en la experiencia personal trabajando con redes neuronales en áreas que les son más “familiares”, la mejor y más confiable opción es el buen descenso de gradiente estocástico con un momento (bien descrito aquí ):

 opt = nk.optimizer.Momentum(learning_rate=1e-2, beta=0.9)

Entrenamiento

NetKet tiene capacitación sin un maestro (nuestro caso) y con un maestro (por ejemplo, la llamada "tomografía cuántica", pero este es el tema de un artículo separado). Simplemente describimos a los "maestros" y eso es todo:

 vc = nk.variational.Vmc( hamiltonian=hamiltonian, sampler=sampler, optimizer=opt, n_samples=1000, use_iterative=True )

El Monte Carlo variacional indica cómo evaluamos el gradiente de la función que estamos optimizando. n_smaples es el tamaño de la muestra de nuestra distribución que devuelve la muestra.

Resultados

Ejecutaremos el modelo de la siguiente manera:

 vc.run(output_prefix=output, n_iter=1000, save_params_every=10)

La biblioteca está construida con OpenMPI, y el script deberá ejecutarse así: mpirun -n 12 python Main.py (12 es el número de núcleos).

Los resultados que recibí son los siguientes:

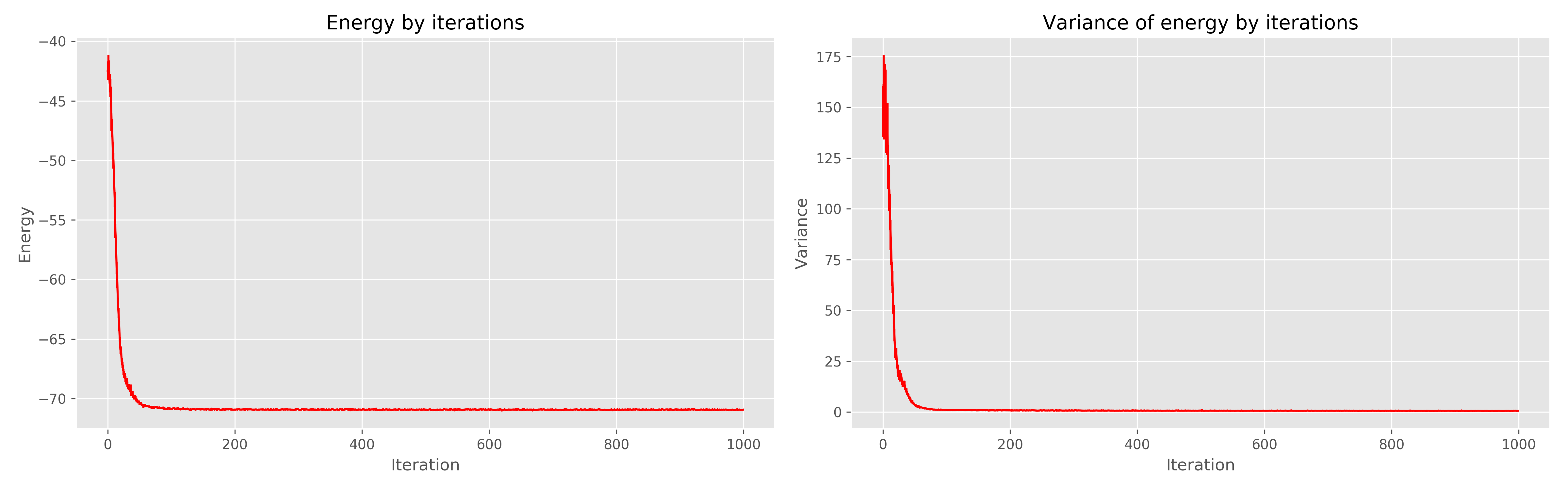
A la izquierda está el gráfico de energía de la era del aprendizaje, a la derecha está la dispersión de energía de la era del aprendizaje.
Se puede ver que 1000 eras son claramente redundantes, 300 habrían sido suficientes. En general, funciona muy bien, converge rápidamente.

Literatura

Orús R. Una introducción práctica a las redes tensoras: estados de productos de matriz y estados de par entrelazados proyectados // Annals of Physics. - 2014 .-- T. 349. - S. 117-158.
Carleo G., Troyer M. Resolviendo el problema cuántico de muchos cuerpos con redes neuronales artificiales // Science. - 2017. - T. 355. - No. 6325. - S. 602-606.
www.netket.org

Estados cuánticos neuronales: representación de una función de onda por una red neuronal