Catálisis de muones en términos de química cuántica. Parte II: electrónica vs. enlace químico muón

Mnogabukaff que la química cuántica piensa en el principio de la catálisis de muones: cómo exactamente el muón reduce la temperatura del plasma deseado. En dos partes (la primera parte se puede leer aquí ).

La esencia de la segunda parte es simple: el muón es más pesado que el electrón, por lo que proporciona un enlace químico más fuerte y un enfoque más cercano de los núcleos, lo que reduce la temperatura del plasma requerida para encender la reacción termonuclear.

Pero aquellos que quieran ver las fórmulas, los gráficos y ver la esencia conceptual de la química cuántica aplicada a las moléculas más simples (cuasi), bienvenidos bajo cat.

Introduccion

En la primera parte (ver aquí ) examinamos la diferencia entre un átomo de hidrógeno $$$\ mathrm {H} ^ \ cdot = \ mathrm {p ^ + e ^ -}$ de su contraparte de muones pesados $$$\ mathrm {p} ^ + \ mu ^ -$ : en el segundo caso, el muón estará atado con más fuerza y ​​se sentará a una distancia más cercana del protón. Al mismo tiempo, examinamos algunas cosas importantes que necesitaremos aquí (formas de orbitales y el sistema atómico de unidades).

En la segunda parte (es decir, aquí) trataremos de entender por qué, cómo y cuánto disminuirá la temperatura del plasma requerida para encender la reacción termonuclear. Las reacciones que nos interesan son:

$$

$$\ mathrm {{} ^ nH + {} ^ m H \ rightarrow} \ \ text {nuevos núcleos + energía}$$

donde n, m = 1,2,3 corresponden a protón, deuterio y tritio, respectivamente. Naturalmente, estos núcleos tienen una carga positiva, por lo que si intenta acercarlos, comenzarán a repeler de acuerdo con la ley de Coulomb (consulte la parte anterior ), y esta es la barrera que impide la aparición de reacciones de fusión. Por cierto, en el caso de las reacciones de desintegración nuclear, esta repulsión tiene el papel opuesto, porque después de la separación del núcleo común, los fragmentos, que se repelen entre sí, adquieren energía cinética adicional, y es esta energía la que se calienta en las centrales nucleares.

Para superar esta barrera de Coulomb, se requiere un aumento en la temperatura del plasma ( T ), que, como todos recuerdan del curso escolar de MKT , está asociado con la velocidad promedio de las partículas en el plasma ( v ) por la fórmula

$$

$$mv ^ 2 = 3k_ \ mathrm {B} T$$

donde m es la masa de partículas, y $$$k_ \ mathrm {B}$ - Constante de Boltzmann .

Pero, imaginemos que hemos combinado dos núcleos de hidrógeno en una determinada partícula, donde ya están ubicados cerca y, por lo tanto, el resto de la barrera para ellos ya es muy pequeña. Entonces necesitaríamos acelerar significativamente estas partículas (léase: necesitamos temperaturas más bajas) para combinarlas en algo nuevo. Y tal papel debería jugar un ion intermedio $$$(\ mathrm {{} ^ nH} \ mu ^ - \ mathrm {{} ^ mH}) ^ +$ , un análogo del ion de una molécula de hidrógeno $$$\ mathrm {H} _2 ^ + = (\ mathrm {He ^ -H}) ^ +$ .
Habiendo examinado las diferencias entre estas dos partículas, nos daremos cuenta de cuán efectivo es el muón para reducir la temperatura de ignición de la fusión termonuclear.

Método MILK MO LKAO

Entonces, tenemos nuestro sistema molecular, que consiste en 2 núcleos de hidrógeno con una carga + e (un módulo de carga de electrones) y una partícula (electrón o muón) con una carga - e . Nuestro sistema, hasta que colisiona con otras partículas, está aislado y, por lo tanto, su energía puede descomponerse en sus partes constituyentes:

$$

$$E = T (\ mathrm {H} _1) + T (\ mathrm {H} _2) + \ underbrace {T (\ mathrm {e} ^ - / \ mu ^ -) + V (\ mathrm {H_1 \ text {from} H_2}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {} \ mathrm {H} _1}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {k} \ mathrm {H} _2})} _ {E_ \ mathrm {e}}$$

donde los dos primeros términos ( $$$T (\ mathrm {H} _1)$ y $$$T (\ mathrm {H} _2)$ ) Es la energía cinética de los núcleos de hidrógeno, el tercer término ( $$$T (\ mathrm {e} ^ - / \ mu ^ -)$ ) Es la energía cinética de una partícula negativa (electrón o muón), el cuarto término $$$V (\ mathrm {H_1 \ text {from} H_2})$ Es la energía de la repulsión de Coulomb de los hidrógenos entre sí, y los dos restantes son la atracción de Coulomb del electrón / muón a cada uno de los protones. En el caso general, este es un problema de 3 cuerpos, solo un problema cuántico. Naturalmente, resolverlo en la frente es muy difícil. Pero, afortunadamente, los núcleos son al menos 1800 veces más pesados ​​que el electrón y 10 más pesados ​​que el muón, por lo que se moverán claramente más lentamente que las pequeñas partículas negativas. Debido a esto, primero puede resolver el problema a su vez: primero, encuentre la energía de los movimientos que no están relacionados con el movimiento de los núcleos, es decir, $$$E_ \ mathrm {e}$ y luego plena energía. Se ve así.

1. Se selecciona la disposición de los núcleos de hidrógeno entre sí, y esto determina las interacciones de Coulomb entre ellos y con el electrón / muón. Potencial de Coulomb $$$V (R) = k \ frac {q_1q_2} {R}$ depende solo de las cargas de partículas $$$q_i$ y la distancia entre ellos, por lo que para todos los isótopos de hidrógeno este valor será el mismo. Además, se resuelve el problema del movimiento de un electrón / muón en el campo de estos núcleos. Esta es la tarea de un solo cuerpo.
2. Estas energías $$$E_ \ mathrm {e}$ se calculan para todos los arreglos posibles de los núcleos entre sí, y esta será la energía potencial de movimiento efectiva de los núcleos. En nuestro caso, necesitamos calcular las energías a diferentes distancias entre sí, por lo que el potencial para un par de núcleos es siempre unidimensional. Bueno, entonces solo necesitamos resolver el problema de dos cuerpos del movimiento de dos isótopos de hidrógeno uno con respecto al otro.

Obviamente, la raíz del problema con nosotros es el cálculo de la energía de electrones / muones en el campo de los núcleos. $$$E_ \ mathrm {e}$ . De hecho, este es el enlace químico: un cierto potencial que mantiene unidos los núcleos en ciertos lugares. Y esta misma tarea de encontrar la energía del enlace químico es la principal en la química cuántica.

Desafortunadamente, tanto el muón como el electrón son partículas cuánticas, por lo tanto, para encontrar esta energía, tenemos que recurrir a los métodos de la mecánica cuántica. De hecho, nuestro problema del movimiento de un electrón / muón en el campo de dos núcleos idénticos se resuelve explícitamente (ver aquí ), pero esta solución es muy complicada y el resultado no es tan claro como en el caso de un átomo similar al hidrógeno. Por lo tanto, intentaremos desmontar un enfoque diferente y aproximado, que sea aplicable a cualquier sistema. Este es el llamado método de orbitales moleculares como combinaciones lineales de orbitales atómicos, o MO LKAO.

Echemos un vistazo más de cerca a la ecuación de Schrödinger para el movimiento de un electrón / muón en el campo de los núcleos de hidrógeno:

$$

$$\ hat {H} \ psi = \ underbrace {\ left (\ overbrace {- \ frac {1} {2m} (\ frac {\ partial ^ 2} {\ partial x ^ 2} + \ frac {\ partial ^ 2} {\ partial y ^ 2} + \ frac {\ partial ^ 2} {\ partial z ^ 2})} ^ {\ hat {T}} + \ overbrace {- \ frac {1} {R_1}} ^ {\ hat {V} _1} + \ overbrace {- \ frac {1} {R_2}} ^ {\ hat {V} _2} + \ overbrace {\ frac {1} {R}} ^ {\ hat {V } _ \ mathrm {HH}} \ right)} _ {\ hat {H}} \ psi = E \ psi$$

Esta ecuación se escribió en el sistema atómico de unidades (ver PS en la parte anterior ), por lo tanto, la carga del núcleo de hidrógeno y el electrón / muón es +1, --1, respectivamente, la masa del electrón es m = 1, y para el muón m ≈207.

Y si observa más de cerca, puede ver que en el Hamiltoniano puede seleccionar una pieza conectada puramente con el movimiento de una partícula negativa alrededor de solo uno de los núcleos, que es solo el Hamiltoniano del átomo de hidrógeno, y esto se puede hacer de 2 maneras:

$$

$$\ hat {H} = (\ overbrace {\ hat {T} + \ hat {V} _1} ^ {\ hat {H} _ {1}} + \ hat {V} _2 + \ hat {V} _ \ mathrm {HH}) = (\ overbrace {\ hat {T} + \ hat {V} _2} ^ {\ hat {H} _ {2}} + \ hat {V} _1 + \ hat {V} _ \ mathrm {HH})$$

Fuera del hamiltoniano de un átomo similar al hidrógeno ( $$$\ hat {H} _i, \ i = $ 1.$ ) siempre tenemos 2 piezas: la energía de interacción de un electrón / muón con otro núcleo ( $$$\ hat {V} _j$ ) y energía de repulsión nuclear ( $$$\ hat {V} _ \ mathrm {HH}$ ) El segundo de ellos no afecta en absoluto el movimiento de los electrones: es solo un cambio de energía en una cierta cantidad, pero la interacción de un electrón con otro núcleo es algo importante.
Podemos imaginar que en cualquier momento nuestra partícula gira solo alrededor de uno de los núcleos, y la interacción con el segundo es solo una corrección. Como método de rotación alrededor de uno de los núcleos, podemos suponer que el electrón / muón está en el estado fundamental (1s), cuya función de onda nos es bien conocida en la parte anterior:

$$

$$| 1s \ rangle = \ frac {1} {\ sqrt {\ pi}} \ exp \ left (- \ frac {R} {R_1} \ right)$$

donde $$$R_1$ Es el radio de Bohr para una partícula. En el caso de un electrón $$$R_1 = 1$ Boro (que es el radio de Bohr para un electrón, igual a aproximadamente 0.5 angstroms), y en el caso de un muón $$$R_1 = \ frac {1} {m_ \ mu} \ aprox \ frac {1} {207}$ .
Para aproximar de alguna manera la función de onda de electrones / muones en el campo de 2 núcleos, podemos intentar tomar la siguiente representación:

$$

$$\ psi \ aprox c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle$$

y luego el problema de resolver una ecuación diferencial parcial compleja con nosotros se reduce a la búsqueda de 2 coeficientes desconocidos c ₁ y c ₂ . Este es el orbital muy molecular presentado como la suma de los coeficientes (una combinación lineal de los científicos) orbitales atómicos 1s.

Naturalmente, necesitamos una ecuación para estos parámetros. Y obtenerlo es bastante simple si sustituyes esta aproximación en la ecuación de Schrödinger $$$\ hat {H} \ psi = E \ psi$ :

$$

$$\ hat {H} (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 \ hat {H} | 1s_1 \ rangle + c_2 \ hat {H} | 1s_2 \ rangle = E (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 E | 1s_1 \ rangle + c_2 E | 1s_2 \ rangle$$

En realidad, queremos que esta proporción se satisfaga en todas partes, por lo que de alguna manera podemos calcular los valores promedio de todo esto. Multiplicamos esta ecuación a la izquierda por $$$<1s_1 |$ y $$$<1s_2 |$ e integrarse sobre todas las coordenadas. Como resultado, obtenemos un sistema de 2 ecuaciones lineales, donde es necesario encontrar los coeficientes c ₁ , c ₂ y energía E :

$$

$$\ begin {pmatrix} \ langle 1s_1 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_1 | \ hat {H} | 1s_2 \ rangle \\ \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} \ langle 1s_1 | 1s_1 \ rangle & \ langle 1s_1 | 1s_2 \ rangle \\ \ langle 1s_2 | 1s_1 \ rangle & \ langle 1s_2 | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

Cualquiera que haya estudiado álgebra lineal reconocerá un problema generalizado de autovector-autovalor. Antes de resolverlo, analizaremos a qué son iguales los elementos de las 2 matrices, la tuta existente (y al mismo tiempo presentamos su breve designación con una letra).

• Comencemos con el más simple: $$$\ langle 1s_1 | 1s_1 \ rangle = \ langle 1s_2 | 1s_2 \ rangle = 1$ - esta es la normalización de las funciones de onda, y como recordamos, la probabilidad total de encontrar un electrón / muón es al menos 1 en alguna parte.
• $$$\ langle 1s_1 | 1s_2 \ rangle = \ langle 1s_2 | 1s_1 \ rangle = S$ - este es el llamado solapamiento integral, que muestra cómo se superponen las nubes de electrones para cada uno de los átomos.
• $$$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle = \ alpha$ . Esta integral consta de varias partes:
  

  $$

  $$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_1 | \ hat {H} _1 | 1s_1 \ rangle} _ {- \ frac {m} {2}} + \ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {1} {R}$$
  
  
• $$$\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ beta$ . Aquí es similar:
  

  $$

  $$\ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_2 | \ overbrace {\ hat {H} _1 | 1s_1 \ rangle} ^ {- \ frac {m} {2} | 1s_1 \ rangle}} {{\ frac {m} {2} S} + \ langle 1s_2 | \ sombrero {V} _2 | 1s_1 \ rangle + \ frac {S} {R}$$
  
  es decir la energía de un átomo similar al hidrógeno y la repulsión internuclear, escalada por la superposición integral (primer y último término) y, por así decir, la energía del salto de electrones / muones de un átomo a otro.
  

Encontremos las expresiones para las energías de nuestro ion similar al hidrógeno de la ecuación reescrita como

$$

$$\ begin {pmatrix} \ alpha & \ beta \\ \ beta & \ alpha \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} 1 & S \\ S & 1 \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

Para encontrar la energía que necesitas para resolver la ecuación:

$$

$$\ det \ begin {pmatrix} \ alpha -E & \ beta -ES \\ \ beta - ES & \ alpha -E \ end {pmatrix} = (\ alpha -E) ^ 2 - (\ beta - ES) ^ 2 = 0$$

donde "det" denota el determinante (determinante de una matriz, en ruso).

Las soluciones de esta ecuación cuadrática con respecto a E son:

$$

$$E_ \ pm = \ frac {\ alpha \ pm \ beta} {1 \ pm S} = - \ frac {m} {2} + \ frac {1} {R} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

La primera pieza es obviamente la energía del átomo, la segunda es la repulsión internuclear, la misma barrera de Coulomb que evita la ignición de la reacción termonuclear, y la última estructura compleja debe ser tratada.

Si descartamos la repulsión internuclear, que es solo un punto de referencia para la energía de electrones / muones, obtenemos que tenemos dos estados con energía

$$

$$\ epsilon_ \ pm = - \ frac {m} {2} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

Dado que ambas funciones de onda $$$| 1s_1 \ rangle$ y $$$| 1s_2 \ rangle$ - positivo, y $$$\ hat {V} _i <0$ (porque la partícula negativa siempre se atrae a la positiva), entonces $$$\ epsilon_ + <- \ frac {m} {2}$ (energía de un solo átomo), y $$$\ epsilon _-> - \ frac {m} {2}$ es decir obtenemos una imagen estándar de los orbitales moleculares:



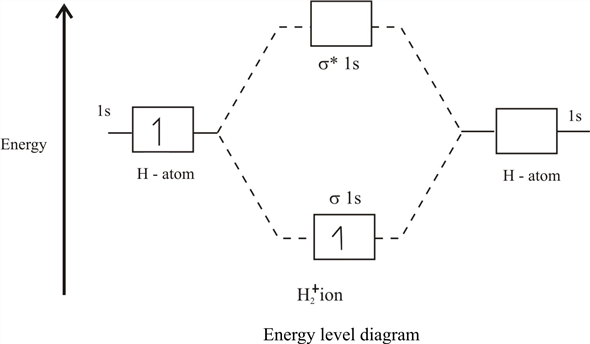
Orbital inferior con energía $$$E _ +$ llamado enlace, y la parte superior (con energía $$$E _-$ ) - anti-vinculante, o aflojamiento. Como resultado, si un electrón / muón se encuentra en el orbital molecular más bajo, entonces se beneficia al volar alrededor de 2 núcleos que alrededor de uno, y con su movimiento disminuye la energía total del sistema. Y este es el enlace químico muy mágico que detecta la repulsión internuclear, permitiendo que los núcleos estén uno al lado del otro durante bastante tiempo.

Y aquí las integrales del enlace químico deben calcularse para comprender cuán cerca se permite que estén los núcleos de hidrógeno. De hecho, las tres integrales buscadas se calculan analíticamente, pero es terriblemente hemorroidal y complicada (cualquiera que esté interesado, vea el Capítulo 9 en el libro de Química Cuántica de Flary ). Por lo tanto, iremos de una manera diferente, más simple, y calcularemos estas integrales numéricamente usando el método de Monte Carlo.

Método Metrópolis

Lo veo muy lógico en el texto sobre la energía termonuclear para rendir homenaje a su abuelo: el átomo militar y, más específicamente, el proyecto Manhattan . Fue de él que creció el método Monte Carlo, y en particular el algoritmo Metropolis , uno de los autores, Edward Teller, es el "padre de la bomba de hidrógeno" (es decir, la persona que lanzó la fusión termonuclear en el atolón Eniwetok ).


En general, analizaremos la esencia del método. Está destinado a las tareas de mecánica estadística. La distribución principal es la distribución de Boltzmann: la probabilidad de detectar un sistema en un determinado estado es $$$\ exp (- \ beta E)$ , $$$\ beta ^ {- 1} = k_ \ mathrm {B} T$ . Y el valor observado de algún parámetro A para el sistema en equilibrio termodinámico es igual a la integral

$$

$$\ langle A \ rangle = \ frac {1} {Z} \ int A (q) \ exp (- \ beta E (q)) dq$$

donde q son las coordenadas que parametrizan el estado del sistema (por ejemplo, las coordenadas / momentos de las partículas), y Z es el factor de normalización llamado función de partición:

$$

$$Z = \ int \ exp (- \ beta E (q)) dq$$

Si hay demasiadas partículas en el sistema, entonces no contar ninguna de las integrales en la frente es completamente poco realista. El ingenuo método de Monte Carlo, en el que simplemente seleccionamos un montón de coordenadas q aleatorias, tampoco dará nada significativo si realmente hay estados posibles del sistema para los cuales la probabilidad $$$\ exp (- \ beta E)$ notablemente no cero, muy pocos. Y es precisamente para tales casos que necesitamos una muestra por significación, en la que permitimos que el algoritmo muestree solo lugares suficientemente probables en el espacio de estado.

El algoritmo Metropolis se ve de la siguiente manera.

1. Al iniciar la simulación, seleccionamos alguna aproximación inicial en el espacio de configuración $$$\ mathbf {q} ^ {(0)}$ y algún vector del incremento máximo posible $$$\ delta \ mathbf {q}$ . En el punto de partida, calculamos la energía del sistema. $$$E ^ {(0)} = E (\ mathbf {q} ^ {(0)})$ (leer - probabilidad $$$p = \ exp (- \ beta E ^ {(0)})$ )
2. La nueva configuración en el enésimo paso es la siguiente.
   
   1. Calcule la energía de la configuración de prueba $$$E_ \ mathrm {trial} = E (\ mathbf {q} _ \ mathrm {trial})$ (es decir, probabilidad $$$p_ \ mathrm {trial} = \ exp (- \ beta E_ \ mathrm {trial})$ )
   2. Y luego comparamos la vieja probabilidad $$$p ^ {(n)}$ con juicio $$$p_ \ mathrm {trial}$
      
      
      • si la nueva configuración tiene una probabilidad mayor o igual ( $$$\ frac {p_ \ mathrm {prueba}} {p ^ {(n)}} \ geq 1$ ), o, de manera equivalente, la energía del nuevo punto es menor o igual que en el antiguo ( $$$E_ \ mathrm {prueba} \ leq E ^ {(n)}$ ), se acepta el nuevo punto y el sistema entra en él ( $$$q ^ {(n + 1)} = q_ \ mathrm {prueba}$ ),
      • si la configuración de prueba es más alta en energía ( $$$E_ \ mathrm {prueba}> E ^ {(n)}$ ), que es equivalente $$$\ frac {p_ \ mathrm {prueba}} {p ^ {(n)}} <1$ , entonces en este caso generamos un número aleatorio $$$P \ en [0; 1)$ de una distribución uniforme, y compárelo con la razón de las probabilidades, que son las probabilidades de transición. Si $$$P <\ frac {p_ \ mathrm {prueba}} {p ^ {(n)}}$ , entonces aceptamos un nuevo punto, y si no ( $$$P \ geq \ frac {p_ \ mathrm {prueba}} {p ^ {(n)}}$ ), luego rechazamos y el sistema permanece en la configuración anterior ( $$$q ^ {(n + 1)} = q ^ {(n)}$ ) ...
      
      
   
   
3. Tomando muchos pasos de acuerdo con el algoritmo anterior, tomamos muestras de una parte significativa (es decir, realmente importante) del posible espacio de configuraciones del sistema. La integral de interés para nosotros se calcula mediante la fórmula:
   $$$\ langle A \ rangle = \ frac {1} {Z} \ int A (\ mathbf {q}) \ exp (- \ beta E (\ mathbf {q})) d \ mathbf {q} = \ frac { 1} {N} \ sum_ {n = 0} ^ {N} A (\ mathbf {q} ^ {(n)})$
   

Así funciona el algoritmo Metropolis.

Y ahora sería necesario adaptarlo al cálculo de las 3 integrales que nos interesan. Echemos un vistazo a ellos con más detalle.

• $$$S (R) = \ langle 1s_2 | 1s_1 \ rangle = \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _2 | } _ {R_2})} _ {1s_2}} ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _1 |} _ {R_1})} _ {1s_1}} ^ {p (\ mathbf {r})} dx dy dz$ donde $$$\ mathbf {r} = (x, y, z) ^ \ mathbf {T}$ - coordenadas del electrón / muón, $$$\ mathbf {r} _i = (x_i, y_i, z_i) ^ \ mathbf {T}$ Son las coordenadas de los núcleos de hidrógeno, y $$$R_i = | \ mathbf {r} - \ mathbf {r} _i | = \ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2}$ - distancias entre partículas positivas y negativas,
  
• $$$\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ límites _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1} \ frac {1} {R_2} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$
• $$$\ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ límites _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_2)} _ {1s_2} \ frac {1} {R_1} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$

Se ve que, si calculamos la función 1s de uno de los átomos para la probabilidad p ,


entonces todo lo demás bajo el signo de la integral (la función de segunda onda y en 2 de 3 casos el potencial de atracción del electrón / muón al núcleo) será una función cuyo valor promedio se calcula. Lo único que tendrá que hacerse, en contraste con el cálculo habitual por el método de Metrópolis, es enderezar la normalización de las integrales. El hecho es que la normalización estándar estará activada

$$

$$Z = \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ exp (-m R) dx dy dz = 4 \ pi \ int \ limits_ {0} ^ {+ \ infty} \ exp (-m R) R ^ 2 dR = \ frac {8 \ pi} {m ^ 3}$$

Y necesitamos normalización para $$$\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}$ donde

$$

$$\ langle 1s_1 | 1s_1 \ rangle = \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ exp (-2 m R) dx dy dz = 4 \ pi \ int \ limits_ {0} ^ {+ \ infty} \ exp (-2m R) R ^ 2 dR = \ frac {\ pi} {m ^ 3} $$$

Esto significa que cada integral calculada de acuerdo con la metrópoli deberá multiplicarse por un factor

$$

$$\ frac {Z} {\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}} = 8 \ sqrt {\ frac {\ pi} {m ^ 3}}$$

Esto ya se puede organizar en forma de una secuencia de comandos determinada, por ejemplo, en Python (por ejemplo, el código está debajo).


Usando tales cálculos, finalmente podemos comparar las energías potenciales en el ion hidrógeno $$$\ mathrm {H} _2 ^ +$ y su homólogo muón.

$$$\ mathrm {H_2 ^ + = p ^ + e ^ - p ^ +}$ vs. $$$\ mathrm {p ^ + \ mu ^ - p ^ +}$

Entonces, armados con un script, podemos calcular la superficie de la energía potencial del enfoque de los núcleos de hidrógeno unidos por un electrón y un muón. Como punto de referencia de energía, tomamos átomos infinitamente diluidos entre sí (es decir, $$$-m / 2$ , que es igual al potencial a la distancia entre los núcleos $$$R = + \ infty$ )

En el caso de un electrón, el potencial cercano al mínimo se ve así:



El mínimo se produce a una distancia de aproximadamente 2 boro (es decir, aproximadamente la suma de 2 radios atómicos), y la energía de disociación de la molécula en fragmentos es de aproximadamente 0,06 Hartree, que corresponde al calentamiento a unos 20,000 grados Kelvin (o Celsius, no importa aquí). Para convertir energías, recomiendo usar recursos en línea, como este .

Una situación similar con un ión de hidrógeno unido muonalmente:



Como el radio de Bohr para el muón hidrógeno es más pequeño (ver la parte anterior ), los núcleos de hidrógeno también se sientan unas 200 veces más cerca de la energía potencial mínima. La energía de descomposición de esta molécula ya es más de 10 Hartree, que corresponde a una temperatura de más de tres grados de lyam ( $$$\ aprox (3.2 \ cdot 10 ^ 6) ^ \ circ$ )

Para la ignición, las reacciones generalmente requieren una temperatura del orden de 10 ⁸ K , que es aproximadamente 320 Hartree. Veamos a qué distancias se logra una energía similar en el caso del ion divodorón ordinario y en el caso de su versión muón:



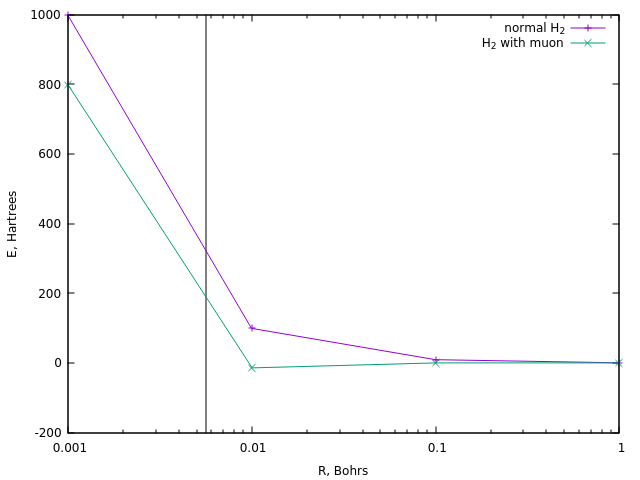
En el caso de los primeros, esto corresponde a una distancia de aproximadamente 0.0058 Boro (línea vertical).

Se alcanza una distancia similar en el muón hidrógeno a una energía de aproximadamente 190 Ha, es decir aproximadamente una vez y media menos. Y esta es la estimación más simple de la temperatura de la catálisis de muones.

Pero, de hecho, todo será aún más genial. El hecho es que si se forma una partícula estable $$$\ mathrm {({} ^ mH (\ mu ^ -) {} ^ nH) ^ +}$ , entonces estos núcleos, mientras el muón está vivo, oscilarán entre sí. Y aquí puede producirse un túnel desde el estado de "dos átomos de hidrógeno" al estado de "núcleo más pesado", y la probabilidad de túnel depende de la longitud de túnel requerida d aproximadamente como $$$p ^ {- d}$ , de modo que al acercar los dos núcleos mediante el muón, aumentaremos en gran medida la probabilidad del curso de túnel de esta reacción. Desafortunadamente, las estimaciones de este efecto ya no requieren química cuántica, sino física nuclear, por lo que esta parte de la discusión está más allá del alcance de esta publicación. Entonces en esto nos detendremos.

PD: ¿Por qué no es tan simple?

De hecho, formar estas partículas no es tan simple en condiciones de plasma. El hecho es que si colisionamos dos partículas, entonces su energía total obviamente excede la energía de disociación (o ionización, en el caso de un núcleo + electrón / muón), por lo que cuando colisionan, no forman una partícula estable (átomo, ion, molécula), sino que pasan volando uno al lado del otro. Para mantenerse unidos, necesitan arrojar energía excedente en algún lugar, y para esto necesitamos un tercer extra que tomará esta energía. Puede ser un fotón, o algún tipo de partícula izquierda volando cerca, pero lo principal es que las condiciones deberían contribuir a este arrastre de exceso de energía.

PPS

Si tiene comentarios / aclaraciones / preguntas, escriba comentarios o PM. Corregiré todo, responderé y explicaré todo.