Entrada
En el
YOW! 2013 uno de los desarrolladores del lenguaje Haskell, el
prof. Philip Wadler mostró cómo las mónadas permiten que los lenguajes funcionales puros realicen operaciones esencialmente imperativas, como la entrada-salida y el manejo de excepciones. No es sorprendente que el interés de la audiencia en este tema haya generado un crecimiento explosivo en las publicaciones sobre mónadas en Internet. Desafortunadamente, la mayoría de estas publicaciones usan ejemplos escritos en lenguajes funcionales, lo que implica que los recién llegados a la programación funcional quieren aprender sobre mónadas. Pero las mónadas no son específicas de Haskell o lenguajes funcionales, y bien pueden ilustrarse con ejemplos en lenguajes de programación imperativos. Este es el propósito de esta guía.
¿En qué se diferencia esta guía del resto? Intentaremos abrir las mónadas en no más de 15 minutos, utilizando solo la intuición y algunos ejemplos elementales de código Python. Por lo tanto, no comenzaremos a teorizar y a profundizar en la filosofía, discutiendo
burritos ,
trajes espaciales ,
escritorios y endofunctores.
Ejemplos motivacionales
Consideraremos tres cuestiones relacionadas con la composición de funciones. Los resolveremos de dos maneras: el imperativo habitual y el uso de mónadas. Luego comparamos los diferentes enfoques.
1. Registro
Supongamos que tenemos tres funciones unarias:
f1 ,
f2 y
f3 , que toman un número y lo devuelven aumentado en 1, 2 y 3, respectivamente. Cada función también genera un mensaje, que es un informe sobre la operación completada.
def f1(x): return (x + 1, str(x) + "+1") def f2(x): return (x + 2, str(x) + "+2") def f3(x): return (x + 3, str(x) + "+3")
Nos gustaría encadenarlos para procesar el parámetro
x , en otras palabras, nos gustaría calcular
x+1+2+3 . Además, necesitamos obtener una explicación legible por humanos de lo que hizo cada función.
Podemos lograr el resultado que necesitamos de la siguiente manera:
log = "Ops:" res, log1 = f1(x) log += log1 + ";" res, log2 = f2(res) log += log2 + ";" res, log3 = f3(res) log += log3 + ";" print(res, log)
Esta solución no es ideal, ya que consiste en una gran cantidad de middleware monótono. Si queremos agregar una nueva función a nuestra cadena, nos veremos obligados a repetir este código de enlace. Además, las manipulaciones con las variables
res y
log perjudican la legibilidad del código, lo que dificulta el seguimiento de la lógica principal del programa.
Idealmente, un programa debería verse como una simple cadena de funciones, como
f3(f2(f1(x))) . Desafortunadamente, los tipos de datos devueltos por
f1 y
f2 no coinciden con los tipos de parámetros
f2 y
f3 . Pero podemos agregar nuevas funciones a la cadena:
def unit(x): return (x, "Ops:") def bind(t, f): res = f(t[0]) return (res[0], t[1] + res[1] + ";")
Ahora podemos resolver el problema de la siguiente manera:
print(bind(bind(bind(unit(x), f1), f2), f3))
El siguiente diagrama muestra el proceso computacional que ocurre en
x=0 . Aquí
v1 ,
v2 y
v3 son los valores obtenidos como resultado de llamadas a
unit and
bind .

La función de
unit convierte el parámetro de entrada
x en una tupla de un número y una cadena. La función de
bind llama a la función que se le pasa como parámetro y acumula el resultado en la variable intermedia
t .
Pudimos evitar repetir el middleware colocándolo en la función de
bind . Ahora, si obtenemos la función
f4 , solo la incluimos en la cadena:
bind(f4, bind(f3, ... ))
Y no necesitamos hacer ningún otro cambio.
2. Lista de valores intermedios.
También comenzaremos este ejemplo con funciones simples unarias.
def f1(x): return x + 1 def f2(x): return x + 2 def f3(x): return x + 3
Como en el ejemplo anterior, necesitamos componer estas funciones para calcular
x+1+2+3 . También necesitamos obtener una lista de todos los valores obtenidos como resultado del trabajo de nuestras funciones, es decir,
x ,
x+1 ,
x+1+2 y
x+1+2+3 .
A diferencia del ejemplo anterior, nuestras funciones son componibles, es decir, los tipos de sus parámetros de entrada coinciden con el tipo del resultado. Por lo tanto, una cadena simple
f3(f2(f1(x))) devolverá el resultado final. Pero en este caso, perdemos los valores intermedios.
Vamos a resolver el problema "de frente":
lst = [x] res = f1(x) lst.append(res) res = f2(res) lst.append(res) res = f3(res) lst.append(res) print(res, lst)
Desafortunadamente, esta solución también contiene mucho middleware. Y si decidimos agregar
f4 , nuevamente tendremos que repetir este código para obtener la lista correcta de valores intermedios.
Por lo tanto, agregamos dos funciones adicionales, como en el ejemplo anterior:
def unit(x): return (x, [x]) def bind(t, f): res = f(t[0]) return (res, t[1] + [res])
Ahora reescribimos el programa como una cadena de llamadas:
print(bind(bind(bind(unit(x), f1), f2), f3))
El siguiente diagrama muestra el proceso computacional que ocurre en
x=0 . Nuevamente,
v1 ,
v2 y
v3 denotan los valores obtenidos de las llamadas de
unit y
bind .

3. Valores vacíos
Intentemos dar un ejemplo más interesante, esta vez con clases y objetos. Supongamos que tenemos una clase de
Employee con dos métodos:
class Employee: def get_boss(self):
Cada objeto de la clase
Employee tiene un administrador (otro objeto de la clase
Employee ) y un salario, al que se accede mediante los métodos apropiados. Ambos métodos también pueden devolver
None (el empleado no tiene un gerente, se desconoce el salario).
En este ejemplo, crearemos un programa que muestre el salario del líder de este empleado. Si no se encuentra al gerente o no se puede determinar su salario, el programa devolverá
None .
Idealmente, necesitamos escribir algo como
print(john.get_boss().get_wage())
Pero en este caso, si alguno de los métodos devuelve
None , nuestro programa finalizará con un error.
Una forma obvia de manejar esta situación podría ser así:
result = None if john is not None and john.get_boss() is not None and john.get_boss().get_wage() is not None: result = john.get_boss().get_wage() print(result)
En este caso, permitimos llamadas adicionales a los
get_wage get_boss y
get_wage . Si estos métodos son lo suficientemente pesados (por ejemplo, acceder a la base de datos), nuestra solución no funcionará. Por lo tanto, lo cambiamos:
result = None if john is not None: boss = john.get_boss() if boss is not None: wage = boss.get_wage() if wage is not None: result = wage print(result)
Este código es óptimo en términos de cómputo, pero se lee mal debido a tres
if anidados. Por lo tanto, intentaremos usar el mismo truco que en los ejemplos anteriores. Definir dos funciones:
def unit(e): return e def bind(e, f): return None if e is None else f(e)
Y ahora podemos poner toda la solución en una línea.
print(bind(bind(unit(john), Employee.get_boss), Employee.get_wage))
Como probablemente ya haya notado, en este caso no tuvimos que escribir la función de la
unit : simplemente devuelve el parámetro de entrada. Pero lo dejaremos para que nos sea más fácil generalizar nuestra experiencia.
Tenga en cuenta también que en Python podemos usar métodos como funciones, lo que nos permitió escribir
Employee.get_boss(john) lugar de
john.get_boss() .
El siguiente diagrama muestra el proceso de cálculo cuando John no tiene un líder, es decir,
john.get_boss() devuelve
None .
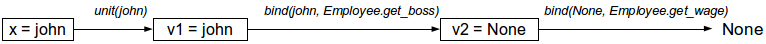
Conclusiones
Supongamos que queremos combinar las funciones del mismo tipo
f1 ,
f2 ,
… ,
fn . Si sus parámetros de entrada son los mismos que los resultados, podemos usar una cadena simple de la forma
fn(… f2(f1(x)) …) . El siguiente diagrama muestra un proceso de cálculo generalizado con resultados intermedios, denotado como
v1 ,
v2 ,
… ,
vn .

A menudo, este enfoque no es aplicable. Los tipos de valores de entrada y resultados de funciones pueden variar, como en el primer ejemplo. O las funciones pueden ser componibles, pero queremos insertar lógica adicional entre llamadas, como en los ejemplos 2 y 3, insertamos una agregación de valores intermedios y una verificación de un valor vacío, respectivamente.
1. Decisión imperativa
En todos los ejemplos, primero utilizamos el enfoque más directo, que puede representarse mediante el siguiente diagrama:

Antes de llamar a
f1 hicimos algo de inicialización. En el primer ejemplo, inicializamos una variable para almacenar un registro común, en el segundo para una lista de valores intermedios. Después de eso, intercalamos llamadas de función con un cierto código de conexión: calculamos valores agregados, verificamos el resultado para
None .
2. Mónadas
Como vimos en los ejemplos, las decisiones imperativas siempre sufrieron de verbosidad, repetición y lógica confusa. Para obtener un código más elegante, utilizamos un cierto patrón de diseño, según el cual creamos dos funciones:
unit y
bind . Esta plantilla se llama
mónada . La función de vinculación contiene middleware mientras la
unit implementa la inicialización. Esto nos permite simplificar la solución final a una línea:
bind(bind( ... bind(bind(unit(x), f1), f2) ... fn-1), fn)
El proceso de cálculo se puede representar mediante un diagrama:

Una llamada a la
unit(x) genera un valor inicial de
v1 . Luego,
bind(v1, f1) genera un nuevo valor intermedio
v2 , que se utiliza en la próxima llamada a
bind(v2, f2) . Este proceso continúa hasta que se obtiene un resultado final. Al definir varias
unit y
bind dentro del marco de esta plantilla, podemos combinar varias funciones en una cadena de cálculos. Las bibliotecas
de mónadas (
por ejemplo, PyMonad u OSlash, aprox. Transl. ) Generalmente contienen mónadas listas para usar (pares de funciones de
unit y
bind ) para implementar ciertas composiciones de funciones.
Para encadenar funciones, los valores devueltos por
unit y
bind deben ser del mismo tipo que los parámetros de entrada de
bind . Este tipo se llama
monádico . En términos del diagrama anterior, el tipo de variables
v1 ,
v2 ,
… ,
vn debe ser de tipo monádico.
Finalmente, considere cómo puede mejorar el código escrito usando mónadas. Obviamente, las llamadas de
bind repetidas parecen poco elegantes. Para evitar esto, defina otra función externa:
def pipeline(e, *functions): for f in functions: e = bind(e, f) return e
Ahora en cambio
bind(bind(bind(bind(unit(x), f1), f2), f3), f4)
podemos usar la siguiente abreviatura:
pipeline(unit(x), f1, f2, f3, f4)
Conclusión
Las mónadas son un patrón de diseño simple y poderoso que se utiliza para componer funciones. En lenguajes de programación declarativos, ayuda a implementar mecanismos imperativos como el registro o la entrada / salida. En idiomas imperativos
ayuda a generalizar y acortar el código que une una serie de llamadas de funciones del mismo tipo.
Este artículo proporciona solo una comprensión superficial e intuitiva de las mónadas. Puede obtener más información comunicándose con las siguientes fuentes:
- Wikipedia
- Mónadas en Python (¡con buena sintaxis!)
- Cronología de los tutoriales de Monad