Geekly articles weekly

Tipos de infinitos y tallo cerebral


Este artículo es una continuación de un artículo sobre grandes números . Pero ahora iremos más allá, en el infinito del infinito.

Para esto necesitamos ZFC : la teoría de los conjuntos Zermelo, Frenkel + Choice. La elección es el axioma de elección, el axioma más controvertido de la teoría de conjuntos. Ella merece un artículo separado. Se supone que sabes cuál es el "poder" del conjunto. Si no, entonces google, seguro que esto se afirma mejor que yo. Aquí solo recordaré algunos

Hechos conocidos


  • El poder de un conjunto de enteros se denota por $ \ aleph_0 $ . Este es el primer poder infinito; tales conjuntos se llaman contables.
  • El poder de cualquier subconjunto infinito de enteros es simple, incluso, etc. - También contable.
  • El conjunto de números racionales, es decir, las fracciones p / q, también es contable; pueden ser pasados ​​por una serpiente.
  • Para cualquier potencia, hay una operación de conjunto de potencia: el conjunto de todos los subconjuntos que crea más potencia que la original. A veces se hace referencia a esta operación como elevar un dos a una potencia, es decir $ powerset (\ aleph_0) = 2 ^ {\ aleph_0} = \ aleph_c $ . El conjunto de potencia de la potencia calculada es la potencia del continuo.
  • El poder continuo está poseído por: segmentos finitos e infinitos, figuras planas y volumétricas, e incluso espacios n-dimensionales en su conjunto.
  • Para las matemáticas ordinarias, el siguiente poder, $ powerset (\ aleph_c) $ prácticamente no es necesario, generalmente todo el trabajo ocurre con conjuntos contables y conjuntos de potencia continua

Ahora

Hechos poco conocidos


En ZFC, no todas las colecciones de elementos pueden ser conjuntos. Hay colecciones tan amplias que es imposible permitir que sean conjuntos; surgen paradojas. En particular, el " conjunto de todos los conjuntos " no es un conjunto. Sin embargo, hay teorías de conjuntos donde tales conjuntos están permitidos.

Más lejos. Teoría de conjuntos ... ¿Qué objetos? Números Una manzana? Naranjas? Por extraño que parezca, ZFC no necesita ningún objeto. Tome el conjunto vacío {} y acuerde que significa 0. 1 denotar por {{}} el deuce como {{{}}} y así sucesivamente. {5,2} es {{{{{{{}}}}}}, {{{}}}}. Usando enteros, podemos crear los reales, y las colecciones de los reales pueden crear cualquier forma.

Entonces la teoría de conjuntos es ... cómo decir ... teoría hueca. Esta teoría no trata de nada. Más precisamente, acerca de cómo puede anidar (anidar, es decir, colocarse entre sí) aparatos ortopédicos.

La única operación definida en la teoría de conjuntos es $ \ en $ - Un símbolo de pertenencia. ¿Pero qué pasa con la unificación, exclusión, igualdad, etc.? Estas son todas las macros, por ejemplo:

$ (A = B) \ equiv \ forall x ((x \ en A) = (x \ en B)) $


Es decir, en traducción al ruso, dos conjuntos se consideran iguales cuando, al probar cualquier elemento para pertenecer a ellos, obtendremos los mismos resultados

Los conjuntos no están ordenados, pero esto se puede arreglar: deje que el par ordenado (p, v) sea {{p}, {p, v}}. Inelegante desde el punto de vista del programador, pero suficiente para un matemático. ¡Ahora el conjunto de todos los pares de valores de parámetros establece una función, que ahora también está configurada! Et voila! ¡Todo análisis matemático, que funciona al nivel de los lenguajes de segundo orden , ya que no habla de la existencia de números , sino de la existencia de funciones , colapsa en un lenguaje de primer orden!

Por lo tanto, la teoría de conjuntos es una teoría pobre sin objetos y con un ícono de relación, que tiene un poder absolutamente monstruoso: sin nuevos supuestos, genera a partir de sí misma aritmética formal, números reales, análisis, geometría y mucho más. Este es un tipo de matemática TOE.

Hipótesis Continua - CH


¿Hay poder entre $ \ aleph_0 $ y $ 2 ^ {\ aleph_0} $ ? Cantor no pudo resolver este problema, el "rey de los matemáticos" Hilbert elogió su importancia, pero solo más tarde se demostró que esta hipótesis no se puede probar ni refutar. Ella es independiente de ZFC.

Esto significa que puede crear dos matemáticas diferentes: una con ZFC + CH, la otra con ZFC + (no CH). De hecho, incluso más de dos. Supongamos que rechazamos CH, es decir, creeremos que entre $ \ aleph_0 $ y $ 2 ^ {\ aleph_0} $ Todavía hay poder. ¿Cuántos puede haber? Uno, dos? Godel creía que solo uno. Pero, como resultó, la suposición de que hay 2, 17, 19393493 de ellos no conduce a contradicciones. ¡Cualquier número, pero no infinito!

Cuando en la aritmética formal nos encontramos con una declaración no demostrable, por ciertas razones sabemos que, sin embargo, esta declaración, aunque no es demostrable, en realidad es verdadera o falsa. En la teoría de conjuntos esto no funciona, realmente tenemos matemáticos diferentes. ¿Cómo relacionarse con esto? Hay tres enfoques filosóficos:

Formalismo: ¿por qué, de hecho, se sorprenderá? Establecemos las reglas del juego de símbolos, reglas diferentes, un resultado diferente. No es necesario buscar un problema donde no existe

Platonismo: ¿Pero cómo explicar que teorías completamente diferentes, como ZFC y New Foundations, basadas en principios completamente diferentes, casi siempre dan el mismo resultado? ¿Significa esto que detrás de las fórmulas hay algún tipo de realidad que estamos estudiando? Esta opinión fue sostenida, por ejemplo, por Godel

Multiverso: podemos tener muchas axiomáticas, a veces dando el mismo resultado, a veces no. Debemos percibir la imagen como un todo: si el color está asociado con diferentes sistemas de axiomas, entonces el árbol de efectos de color es la matemática. Si algo es cierto en todas partes, es blanco, pero también hay ramas de colores.

Más y más alto.


En el futuro, por simplicidad, aceptaremos la hipótesis del continuo, es decir $ powerset (\ aleph_0) = \ aleph_1 = \ aleph_c $ - Es muy conveniente. De hecho, también aceptaremos el axioma más fuerte, la hipótesis del continuo generalizado de que entre x y el conjunto de potencia (x) nunca hay potencias intermedias. Ahora iteramos el conjunto de potencia y todo es simple:

$ \ aleph_0 \ rightarrow \ aleph_1 \ rightarrow \ aleph_2 \ rightarrow ... \ rightarrow \ aleph_ {36463634} \ rightarrow $


¿Hasta dónde podemos llegar? Después de un número infinito de iteraciones, llegamos a $ \ aleph_ \ omega $ - poder infinito en orden! Por cierto, su existencia no era obvia para Cantor. Pero un segundo! Después de todo, la función powerset siempre está definida, por lo tanto $ \ aleph_ \ omega $ No puede ser el último!

$ \ aleph_ \ omega \ rightarrow \ aleph _ {\ omega + 1} \ rightarrow \ aleph _ {\ omega + 2} \ rightarrow ... $


Para obtener $ \ aleph _ {\ omega + 3} $ Es necesario repetir el powerset infinito y tres veces más . ¿Ya has comenzado a demoler el techo? O de lo contrario lo será. Porque nuevamente, habiendo iterado el conjunto de potencia un número infinito de veces, llegamos a $ \ aleph _ {\ omega + \ omega} = \ aleph _ {\ omega2} $ , después de lo cual, naturalmente, $ \ aleph _ {\ omega2 + 1} $

Habiendo alcanzado el infinito un número infinito de veces , obtenemos el índice $ \ omega ^ 2 $ . ¿Cómo te gusta este poder, por ejemplo: $ \ aleph _ {\ omega ^ 3 + \ omega ^ 2 + \ omega4 + 48745} $ ? Mientras iteramos powerset sobre la lista de ordinales, aquí están los ordinales iniciales:

imagen

Pero hay muchos, muchos más. Así que nos saltaremos todo de inmediato y lo haremos

Gran paso de inmediato


Atencion ¡Lo que está escrito a continuación puede ser peligroso para su cerebro! Repetimos el conjunto de potencia varias veces, pero ¿no saludamos al continuo ? Honestamente, yo mismo soy un poco salchicha por el hecho de que el ciclo se puede realizar de forma continua, pero la teoría de conjuntos requiere existencia

$ \ aleph _ {\ aleph_1} $


A continuación iremos más rápido:

$ \ aleph _ {\ aleph_1} \ rightarrow \ aleph _ {\ aleph_2} ... \ rightarrow \ aleph _ {\ aleph_ \ omega} = \ aleph _ {\ aleph_ \ aleph} \ rightarrow $


El último Alef tiene un índice cero, pero el látex local no permite que se ponga, hay demasiados niveles. Pero lo principal es que entendiste, no importa cuánto poder monstruoso creamos, podemos decir: sí, esto es solo un repetidor y poner toda esta construcción en forma de índice para el nuevo Aleph. Ahora las capacidades están creciendo como una bola de nieve, no podemos detenernos, la pirámide de Alephs es más alta y podemos crear cualquier poder ... ¿O no?

Poder inalcanzable


¿Qué pasa si hay un poder tan grande? $ \ theta $ que no importa cómo intentemos alcanzarlo "desde abajo", construyendo estructuras desde Alephs, ¿no lo lograremos? Resulta que la existencia de tal poder es independiente de ZFC. Puedes aceptar su existencia o no.

Escucho el susurro de la navaja de Occam ... No, no. Los matemáticos se adhieren al principio opuesto, que se llama maximalismo ontológico : dejar que todo lo posible exista. Pero hay al menos dos razones más por las que quiero aceptar esta hipótesis.

  • En primer lugar, este no es el primer poder inalcanzable que conocemos. Primero ... este es el poder familiar de contar. Por extraño que parezca, tiene todas las propiedades inalcanzables, simplemente no es habitual llamarlo así:
  • No hay forma de obtener potencia infinita “desde abajo”: ni agregar elementos una cantidad finita de veces, ni iterar powerset () una cantidad finita de veces, utilizando conjuntos finitos para la siembra, no obtendrá infinito. Para obtener el infinito, ya debes tenerlo en alguna parte.
  • La existencia del poder infinito es introducida por un axioma especial: el axioma del infinito. Sin ella, la existencia del poder infinito no se puede probar.


Segundo: si rechazamos el axioma del infinito, obtenemos FinSet, una teoría simple de conjuntos de juguetes con conjuntos finitos. Vamos a escribir todos estos conjuntos (el llamado modelo de teoría )

{}
{{}}
{{{}}, {}}
{{{{}}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}, {}}
...

Y obtenemos ... un conjunto infinito de conjuntos finitos ... Es decir, el modelo de la teoría de los conjuntos finitos es infinito y desempeña el papel de "el conjunto de todos los conjuntos" en él. Tal vez esto ayude a entender por qué la teoría no puede hablar sobre el "conjunto de todos los conjuntos": tal conjunto siempre existe como un modelo fuera de la teoría y tiene otras propiedades que los conjuntos dentro. No se puede agregar el infinito a la teoría de conjuntos finitos.

Y si $ \ theta $ es la "multitud de todas las multitudes" de la teoría ZFC. En este video, al final se dice muy bien sobre el poder inalcanzable, pero tenemos que continuar.

Aún más lejos.


Por supuesto, podemos ir más allá iterando $ powerset (\ theta) $ . Después de seguir todos los pasos descritos anteriormente, construir enormes torres repetidoras, nuevamente nos encontramos con un cardenal inalcanzable (pero ahora no necesitamos nuevos axiomas, con el axioma de la existencia de poder inalcanzable que acabamos de agregar, esto se ha vuelto demostrable). Y una y otra vez.

$ \ theta_0 \ rightarrow \ theta_1 \ rightarrow \ theta_2 \ rightarrow ... \ rightarrow \ theta_ {36463634} \ rightarrow $

Tenga en cuenta que ahora la flecha no tiene sentido para nosotros como ejecutar la función Powerset (), pero GetNextInaccessible (). De lo contrario, todo se ve muy similar, tenemos:

$ \ theta _ {\ theta_1} \ rightarrow \ theta _ {\ theta_2} ... \ rightarrow \ theta _ {\ theta_ \ omega} \ rightarrow \ theta _ {\ theta_ \ theta} \ rightarrow $



Ahora definitivamente lograremos algo ... ¿O no?

Jerarquía de grandes capacidades.


Sí, con GetNextInaccessible nos encontramos con un poder hiper-inalcanzable. Su existencia requiere un axioma más. Hay poderes hiper-hiper-inalcanzables. Y así sucesivamente. Pero hay otras formas de determinar el poder , no solo a través de la inalcanzabilidad:



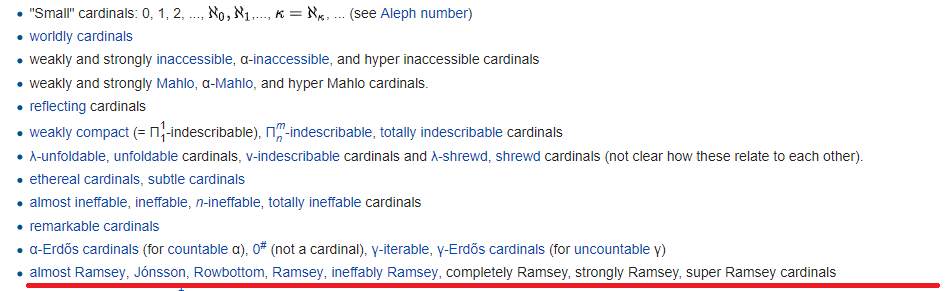
Detrás de cada enlace hay, por regla general, una jerarquía interminable con un número arbitrario de prefijos de hiper y repetidores. Sin embargo, el número total de fórmulas que determinan los cardenales inalcanzables no es tan grande, ¡porque el número de fórmulas es contable! Por lo tanto, tarde o temprano terminarán. Donde terminan, se dibuja una línea roja. Todo debajo de esta línea se define de manera más inestable, aunque formalmente.

La línea roja marca el final del universo de Gödel (pero no olvides que Gödel creó DOS universos diferentes), el universo de conjuntos construidos desde abajo usando fórmulas. Las capacidades por encima de la línea roja se denominan hmm, "pequeño" y debajo - grande:



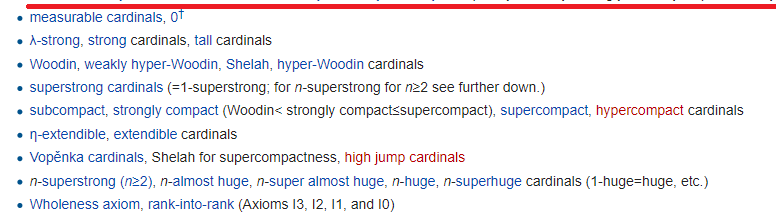
La idea principal en ellos es que el universo de conjuntos se vuelve tan grande que comienza a repetirse en diferentes sentidos. Cada línea, como siempre, requiere un axioma separado y varios. Y lo que es más interesante, todo esto no es tan inútil como podría pensar. Por ejemplo, el axioma más fuerte (rango en rango), en la línea de fondo, es necesario para probar el hecho sobre las tabletas .

A continuación se muestra una encuesta, la última opción se descifra aquí .

Source: https://habr.com/ru/post/445904/

More articles:


All Articles