No, bueno, por supuesto, no hablo en serio. Debe haber un límite en qué medida es posible simplificar el tema. Pero para las primeras etapas, una comprensión de los conceptos básicos y una "entrada" rápida en el tema, puede ser permisible. Y cómo nombrar adecuadamente este material (opciones: "Aprendizaje automático para tontos", "Análisis de datos de los pañales", "Algoritmos para los más pequeños"), lo discutiremos al final.
A los negocios. Escribió varios programas de aplicación en MS Excel para la visualización y visualización de procesos que ocurren en diferentes métodos de aprendizaje automático al analizar datos. Ver es creer, al final, según los medios de comunicación de la cultura que desarrolló la mayoría de estos métodos (por cierto, de ninguna manera todos. El "método de vector de soporte" más poderoso, o SVM, máquina de vectores de soporte es una invención de nuestro compatriota Vladimir Vapnik, Instituto de Administración de Moscú. 1963, por cierto, ahora él, sin embargo, enseña y trabaja en los Estados Unidos.
Tres archivos para revisión
1. K-significa agrupamiento
Las tareas de este tipo se relacionan con "aprender sin un maestro", cuando necesitamos dividir los datos iniciales en un cierto número de categorías conocidas de antemano, pero no tenemos ninguna cantidad de "respuestas correctas", debemos extraerlas de los datos en sí. El problema clásico fundamental de encontrar una subespecie de flores de iris (Ronald Fisher, 1936!), Que se considera el primer signo de este campo de conocimiento, es de tal naturaleza.
El método es bastante simple. Tenemos un conjunto de objetos representados como vectores (conjuntos de N números). Para los iris, este es un conjunto de 4 números que caracterizan una flor: la longitud y el ancho de los lóbulos periantio externo e interno, respectivamente (
Iris Fisher - Wikipedia ). Como una distancia, o medida de proximidad entre objetos, se elige la métrica cartesiana habitual.
Además, los centros de los grupos se seleccionan arbitrariamente (o no arbitrariamente, ver más abajo), y se calculan las distancias desde cada objeto a los centros de los grupos. Cada objeto en este paso de iteración se marca como perteneciente al centro más cercano. Luego, el centro de cada grupo se transfiere a la media aritmética de las coordenadas de sus miembros (por analogía con la física también se le llama "centro de masa"), y el procedimiento se repite.
El proceso converge lo suficientemente rápido. En las imágenes en dos dimensiones, se ve así:
1. La distribución aleatoria inicial de puntos en el plano y el número de grupos

2. Definir los centros de los grupos y asignar puntos a sus grupos.
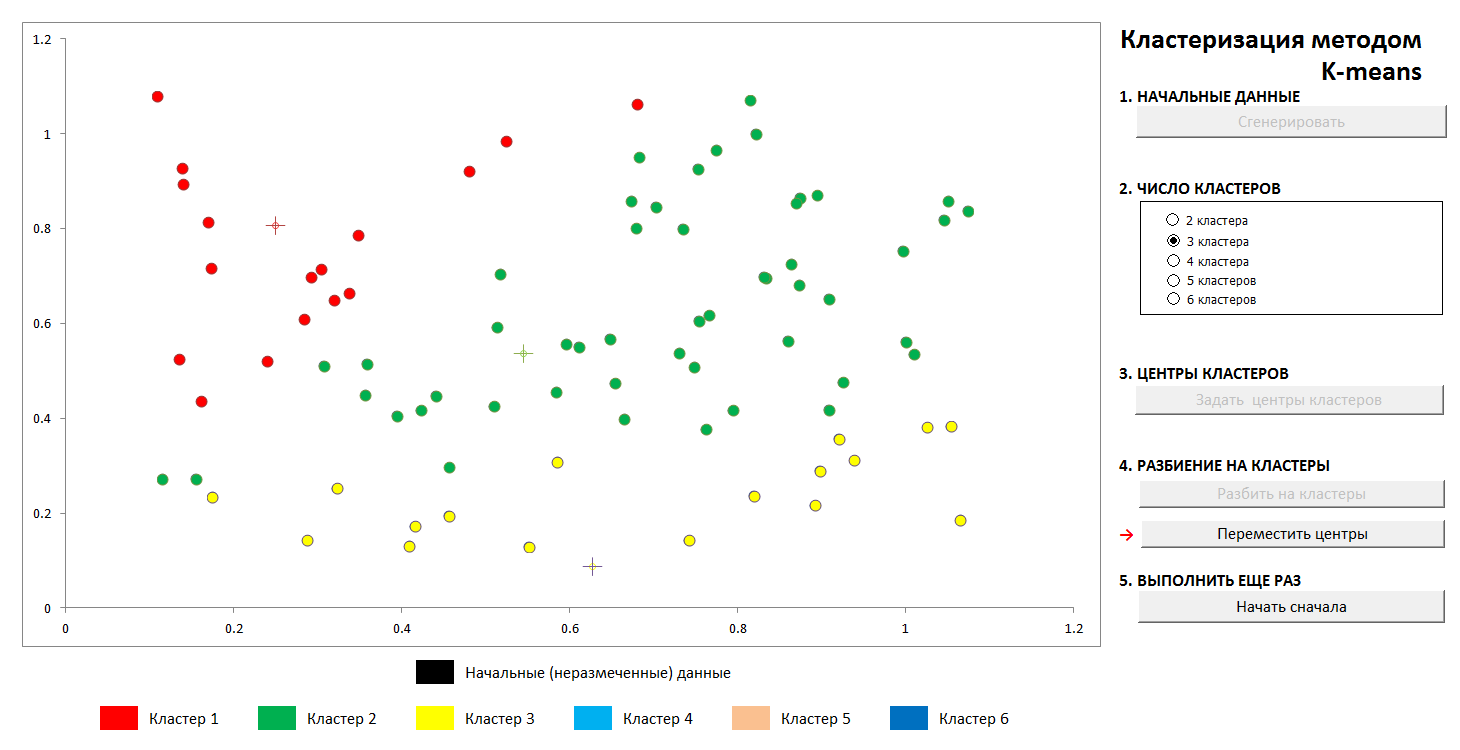
3. Transferencia de coordenadas de los centros de agrupaciones, recálculo de los puntos, hasta que los centros se estabilicen. La trayectoria del centro del grupo a la posición final es visible.

En cualquier momento, puede establecer nuevos centros de clúster (¡sin generar una nueva distribución de puntos!) Y ver que el proceso de partición no siempre es único. Matemáticamente, esto significa que para la función optimizada (la suma de los cuadrados de las distancias desde los puntos a los centros de sus grupos) no encontramos un mínimo global, sino local. Este problema se puede vencer ya sea mediante una elección no aleatoria de los centros iniciales de los grupos, o clasificando los posibles centros (a veces es ventajoso colocarlos exactamente en algún momento, entonces al menos hay una garantía de que no obtendremos grupos vacíos). En cualquier caso, un conjunto finito siempre tiene un límite inferior exacto.
Puede jugar con este archivo en este enlace (no olvide habilitar el soporte de macros. Se comprueban los archivos en busca de virus)
Descripción del método de Wikipedia - método
k-means2. Aproximación por polinomios y desglose de datos. Reentrenamiento
Un notable científico y divulgador de la ciencia de datos K.V. Vorontsov habla brevemente sobre los métodos de aprendizaje automático como "la ciencia de dibujar curvas a través de puntos". En este ejemplo, encontraremos el patrón en los datos mediante el método de mínimos cuadrados.
Se muestra la técnica de dividir los datos de origen en "entrenamiento" y "control", así como en un fenómeno como el reentrenamiento o "reentrenamiento" de los datos. Con la aproximación correcta, tendremos un cierto error en los datos de entrenamiento y un error ligeramente mayor en los datos de control. Si está mal, es un ajuste fino para los datos de entrenamiento y un gran error en el control.
(Es un hecho bien conocido que a través de N puntos es posible dibujar una sola curva del N-1er grado, y este método generalmente no da el resultado deseado. El
polinomio de interpolación de Lagrange en Wikipedia )
1. Establecemos la distribución inicial

2. Divida los puntos en "entrenamiento" y "control" en una proporción de 70 a 30.

3. Dibujamos una curva aproximada para los puntos de entrenamiento, vemos el error que da en los datos de control

4. Dibujamos la curva exacta a través de los puntos de entrenamiento, y vemos un error monstruoso en los datos de control (y cero en el entrenamiento, pero ¿cuál es el punto?).

Por supuesto, se muestra la variante más simple con una sola partición en subconjuntos de "entrenamiento" y "control", en el caso general esto se hace repetidamente para el mejor ajuste de los coeficientes.
El archivo está disponible aquí, antivirus verificado. Activar macros para que funcionen correctamente
3. Descenso de gradiente y dinámica de error
Habrá un caso de 4 dimensiones y regresión lineal. Los coeficientes de regresión lineal se determinarán en pasos por el método de descenso de gradiente, inicialmente todos los coeficientes son ceros. Un gráfico separado muestra la dinámica de la reducción de errores a medida que los coeficientes se ajustan cada vez más. Es posible ver las cuatro proyecciones bidimensionales.
Si configura el paso de descenso de gradiente demasiado grande, entonces está claro que cada vez que salteamos el mínimo y llegaremos al resultado en un mayor número de pasos, aunque al final llegaremos de todos modos (a menos que toquemos demasiado el paso de descenso, entonces el algoritmo irá " en el espaciado "). Y el gráfico de la dependencia del error en el paso de iteración no será uniforme, sino "desigual".
1. Generar datos, establecer el paso de descenso del gradiente
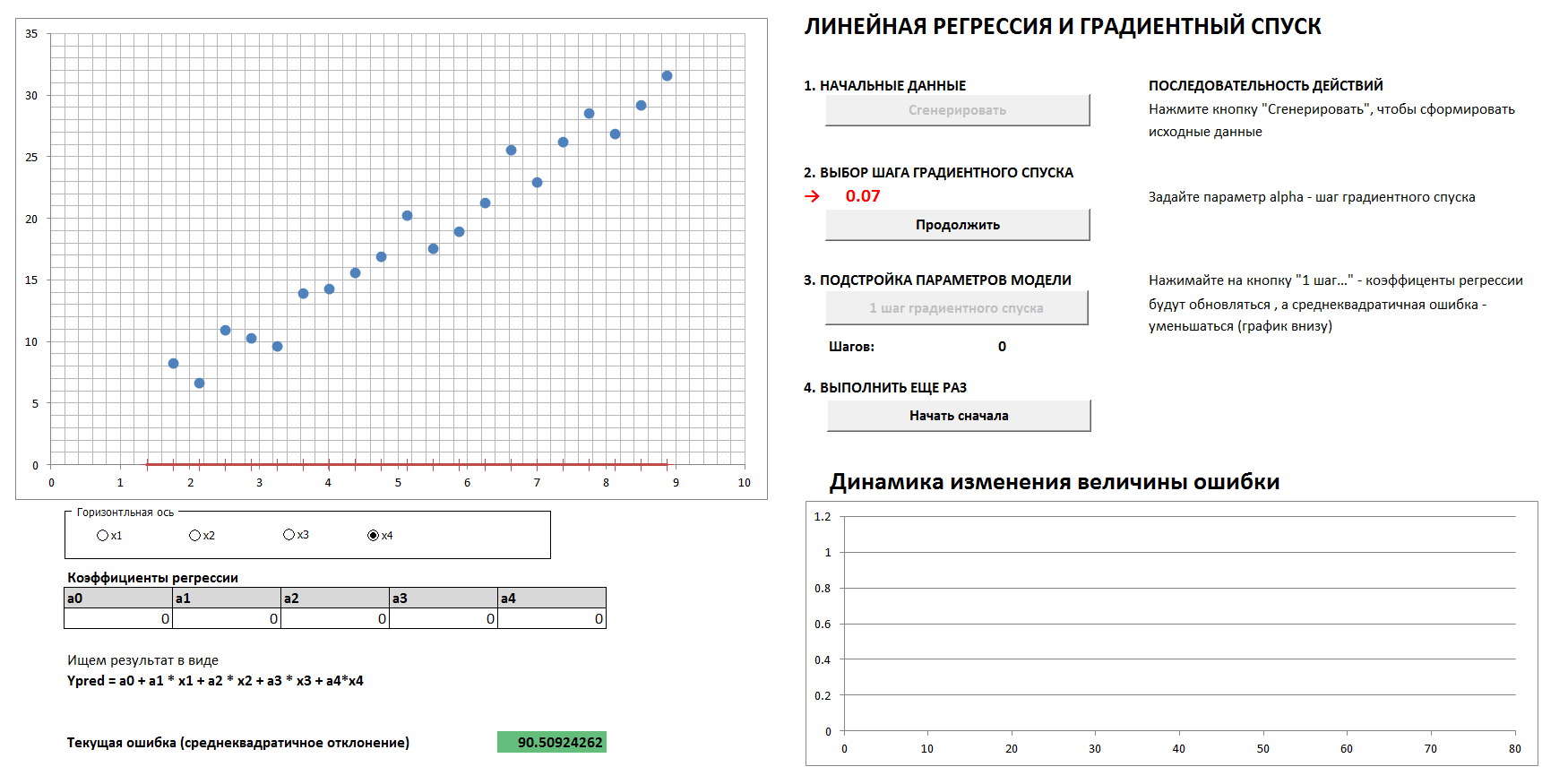
2. Con la elección correcta del paso de descenso de gradiente, llegamos a un mínimo de manera suave y rápida

3. Si el paso de descenso de gradiente se selecciona incorrectamente, omitimos el máximo, el gráfico de error es "desigual", la convergencia toma un mayor número de pasos

y

4. Con una selección completamente incorrecta del paso de descenso del gradiente, nos alejamos del mínimo

(Para reproducir el proceso con los valores del paso de descenso de gradiente que se muestran en las imágenes, marque la casilla "datos de referencia").
Archivo: mediante este enlace, debe habilitar las macros, no hay virus.Según una comunidad respetada, ¿es aceptable tal simplificación y método de presentación? ¿Debo traducir el artículo al inglés?