Es difícil repensar el concepto de una tarea, pero el resultado lo vale.
 Nota del autor
Nota del autor : Sé que calculé incorrectamente la transferencia de Bragg tanto en el caso clásico como en el cuántico; sin embargo, está lo suficientemente cerca de la verdad para comprender la diferencia entre programar computadoras clásicas y cuánticas.
Tiempo: en algún lugar en 2018. Ubicación: canal podrido en Slaka.
"¿Conoces Python?"
Las preguntas de John Timmer, el director científico de Ars Technica, a veces pueden ser tomadas por sorpresa. Si fuera posible impregnar letras en Slaka con precaución, entonces mi respuesta "Sí" simplemente rezumaría con eso.
Resulta que D-Wave decidió dar acceso al mundo a su optimizador cuántico a través de la API. Ars lo invitó a intentarlo, pero necesitabas saber Python. Estaba listo para eso.
Asumí que D-Wave lanzaría algún tipo de API fantástica que podría tomar mi código propietario, lo que hace llorar a los programadores, y convertirlo en líneas cuánticas optimizadas. Por desgracia, cuando llegué al optimizador cuántico, resultó que no era así. Rápidamente me encontré inmerso en la documentación, tratando de descubrir qué tenía que hacer.
Creo que el representante de relaciones públicas de D-Wave tenía en mente a una persona que sabía lo suficiente como para ejecutar ejemplos ya hechos. Pero soy terco. Necesitaba pensar en tres o cuatro tareas posibles que quisiera probar. Quería averiguar: ¿puedo dominar el proceso de resolución de estos problemas en una computadora D-Wave? ¿Qué tan fácil es dar un salto conceptual desde la programación clásica hasta trabajar con recocido cuántico? ¿Al menos algunas de mis tareas se adaptarán a esta máquina?
Revelando una conclusión asombrosa de inmediato, diré que las respuestas fueron las siguientes: tal vez no es realmente "dominar"; dificil No todas las tareas.
Elección de tareas para la programación.
A pesar de la forma en que me imaginas, me pueden llamar programador en ejercicio. Esencialmente, cualquier persona con una buena comprensión de la programación haría una mueca (y posiblemente cometería un asesinato) cuando vi mi código de Python.
Sin embargo, puedo proponer tareas que requieran escribir un programa para resolverlas. Necesito, por ejemplo, algo que calcule el campo eléctrico de un conjunto de electrodos. Algo que encuentra un estado con una energía mínima de átomo de helio. O algo que cuente el aumento de la intensidad de la luz al comienzo del láser. Estas tareas me interesan más. Y al comenzar este proyecto, no tenía idea de si la arquitectura D-Wave podría resolver estos problemas.
Elegí dos problemas que, en mi opinión, podrían funcionar: encontrar miembros del conjunto de Mandelbrot y calcular los contornos potenciales de un conjunto de electrodos. La ventaja de estos problemas era que podía resolverlos rápidamente usando el código clásico y comparar las respuestas. Pero rápidamente me encontré con problemas tratando de descubrir cómo comenzar a resolver estos problemas en una máquina de D-Wave. Requiere un cambio importante en la comprensión de las tareas, y mi pensamiento funciona de manera bastante directa.
Por ejemplo, uno de los problemas que encontré es que estamos tratando con números binarios de bajo nivel (a pesar del hecho de que se expresan en forma de qubits, no bits). Esto significa que, de hecho, el programa no tiene tipos. Casi toda mi experiencia en programación ha sido resolver problemas físicos utilizando tipos numéricos de coma flotante.
Tenemos que pensar de manera diferente sobre el problema: la respuesta debe expresarse como un número binario (idealmente, verdadero o falso), y toda la física (por ejemplo, todos los números de coma flotante) debe expresarse mediante una combinación de qubits. Incluso si mi vida dependiera de ello, no sería capaz de descubrir cómo se puede hacer esto en ninguna de mis tareas. Inmerso en la enseñanza, permití que este problema hirviera un poco en mi propio jugo.
Seis meses después, finalmente encontré un problema con el que estaba familiarizado y que podía resolver con una computadora D-Wave. El paso de la luz a través de una rejilla de fibra de Bragg puede expresarse como un problema binario: ¿salió un fotón del filtro o no? Toda la física está contenida en compuestos qubit, y la respuesta se extrae de la energía de la solución.
Rejillas Bragg
Una rejilla Bragg unidimensional es un material multicapa. Cada espacio entre las dos capas refleja una pequeña cantidad de luz. La penetración total a través de toda la estructura está determinada por la distancia entre los espacios. Para que la luz pase, es necesario que las ondas de diferentes intervalos se sumen en fase. A continuación se muestra el espectro de paso de una rejilla Bragg ideal con 50 capas y una reflectancia del 0.1%.
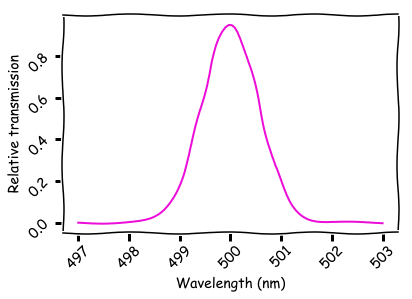
El siguiente código genera datos para este gráfico:
ld = np.linspace(ld_center-3e-9, ld_center+3e-9, num_ld) k = 2*np.pi/ld T = np.ones(ld.shape) for j in range(num_layers): T = T*(1-A)*np.cos(j*k*layer_sep)**2
Aquí calculamos explícitamente las contribuciones relativas de cada espacio, expresadas en potencia óptica, que alcanzan el siguiente espacio. La interferencia constructiva y destructiva se tiene en cuenta al reducir o aumentar la contribución del espacio, dependiendo de qué tan cerca coincida la distancia entre las capas con la mitad de la longitud de onda.
Este truco es necesario porque la conexión de qubits se expresa solo en números reales y no en números complejos (la física se expresa mejor a través de números complejos que contienen la amplitud y la fase de la luz). Sin embargo, la salida del código clásico parece aproximadamente correcta: la ausencia de bandas de frecuencia laterales preocupa un poco, lo que indica la incompletitud del modelo, pero hasta ahora no importa.
El código del modelo clásico carece de verificaciones de consistencia. Calculé el resultado, sugiriendo exactamente cómo se propagaría la onda. Incluso si esta suposición resulta ser incorrecta, el resultado del cálculo será el mismo, aunque todas las ecuaciones se basan en la física, es imposible garantizar en el código que lo describan correctamente.
Pasamos a quanta
En el sistema D-Wave, es necesario crear una cadena de qubits, cada uno de los cuales representa la intensidad de la luz en el espacio. Cada qubit está asociado con sus vecinos, y el peso de la conexión representa el paso de un hueco a otro, teniendo en cuenta la distancia entre las interfaces. Si la distancia entre las interfaces es igual a la mitad de la longitud de onda, la luz puede resonar entre las dos interfaces y pasar. Si la distancia es un cuarto de la longitud de onda, se activa una interferencia destructiva y la conexión debe ser mínima.
El paso a través de una brecha se indica en 99.9%, por lo que la conexión entre el cero y los primeros qubits es
P0,1=0,999cos2(2 pid/ lambda)
Entre el primero y el segundo:
P1,2=P0,10,999cos2(4 pid/ lambda)
Entre el segundo y el tercero:
P2,3=P1,2P0,10,999cos2(6 pid/ lambda)
En esta fórmula, d es la distancia física entre las capas y λ es la longitud de onda. Si d / λ = 0.5, entonces el coseno es igual a la unidad, y podemos esperar la transmisión ideal de la luz.
En el sistema D-Wave, esto significa que cada dos qubits vecinos deben conectarse de la siguiente manera:
Pi,j=[0,999cos2(2i pid/ lambda)]i
En esta expresión, el grado u tiene en cuenta la influencia de qubits anteriores y simplifica el esquema de conexión.
Implementación de tareas
Ahora, sabiendo cómo conectar qubits, debemos observar la conexión física de qubits para decidir cómo completar esta tarea. Esto se llama incrustación menor.
Debemos darle a la computadora una lista de conexiones entre qubits con sus pesos. También debemos especificar las desviaciones que indican la importancia de cada qubit. En nuestro caso, todos los qubits son igualmente importantes, por lo tanto, se establecen como -1 para todos los qubits (tomé este número del ejemplo estándar). Las desviaciones y conexiones deben estar asociadas con qubits físicos y las relaciones entre ellos. En el caso de tareas grandes, la búsqueda de dicha asignación puede llevar mucho tiempo.
El código para generar relaciones y desviaciones es bastante simple.
Afortunadamente, la API de D-Wave intentará encontrar una pequeña implementación por su cuenta. Descubrí que funcionaba para un filtro con 50 capas, pero no podía hacer frente a 100 capas. Esto me parece bastante extraño, ya que tener 2,000 qubits y una longitud de cadena de 1 (no necesitamos combinar varios qubits físicos para crear uno lógico), el sistema debe ser capaz de implementar problemas aún mayores. Mirando hacia atrás, creo que la falla se debió al hecho de que pedí demasiadas conexiones cero.
Un enfoque alternativo es simplemente no definir explícitamente los enlaces nulos. Esto le da al algoritmo la libertad de encontrar más opciones de implementación donde los qubits no tienen conexiones. No he intentado esto, pero esta opción me parece el siguiente paso lógico.
En cualquier caso, iniciar la máquina D-Wave es muy simple:
response = EmbeddingComposite(DWaveSampler()).sample_qubo(Q_auto, num_reads=num_runs)
Aprendiendo a hablar cubitly
La diferencia entre mi algoritmo clásico y la solución D-Wave es que la computadora D-Wave no devuelve directamente un resultado claro. Resulta roto en muchas partes. Obtenemos una lista de energías, y la más pequeña de ellas debería ser la solución. Para varias corridas (digamos 1000) para cada energía, obtenemos el número de veces que apareció en la respuesta. Y para cada ejecución obtenemos una "respuesta", el valor de qubits. No me quedó claro de inmediato cuál de estos valores puede (y puede) interpretarse como pasar a través de un filtro.
Al final, decidí que la energía de solución mínima sería la mejor respuesta, ya que este valor en cierto sentido representa la cantidad de energía almacenada en el filtro. Por lo tanto, una solución con mayor energía representa una mayor permeabilidad del filtro, como se muestra a continuación. Convertir esta respuesta en un verdadero pasaje de luz se deja como tarea para aquellos que entienden esto.

También es posible obtener una representación física del proceso examinando los valores de qubits en una solución con la energía más baja. A continuación puede ver los valores de bits de las soluciones correspondientes al pico de la curva de transmisión (500 nm), 50% de transmisión (500.6 nm) y 5% de transmisión (501.4 nm).
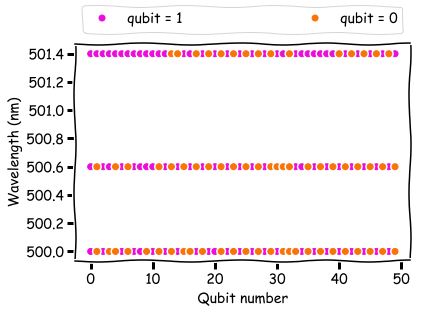
En el borde del pico de transmisión, los qubits tienden a acumularse en grupos de unidades. En el pico, los qubits alternan entre 0 y 1. Esta última solución es una imagen binaria de cómo varía la intensidad de la luz en la rejilla de Bragg. En otras palabras, la solución D-Wave también presenta la física directamente, lo que no se puede decir sobre mi código clásico.
Esta es la verdadera fuerza del recocido cuántico. Sí, puedo derivar perfectamente la curva de pasar por el filtro a partir de cálculos clásicos. Pero para tener una idea de lo que realmente está sucediendo en el interior, necesita un código más complejo. Y en el recocido cuántico, esto es completamente gratis. En mi opinión, esto es muy bueno.
Otra ventaja del recocido cuántico es que garantiza una solución consistente dentro del marco de mi elección de ponderaciones de bonos qubit. Esto significa que es probable que la solución de una computadora cuántica sea más confiable que la solución obtenida del código clásico.
Debates sobre programación cuántica
La parte más difícil de programar una máquina D-Wave es que necesita pensar de manera diferente sobre las tareas. Por ejemplo, me acostumbré a los problemas de minimización cuando la curva coincide con los datos. Pero me resultó muy difícil cambiar su forma de pensar sobre un problema físico para comenzar a escribir código para resolverlo. No ayuda que la mayoría de los ejemplos dados por la compañía me parezcan abstractos y no adaptables a los problemas físicos. Pero esta situación cambiará cuando más y más usuarios comiencen a publicar su código.
Además, pueden surgir dificultades con la interpretación de la respuesta. Básicamente, me gustó la simplicidad de la API, y es genial obtener ideas adicionales de forma gratuita. En un futuro cercano, podría usar D-Wave para resolver problemas reales.