"¿Qué clase de demonio debería recordar de memoria todos estos malditos algoritmos y estructuras de datos?"
Sobre esto se reduce a los comentarios de la mayoría de los artículos sobre el paso de entrevistas técnicas. La tesis principal, por regla general, es que todo lo utilizado de una forma u otra ya se ha implementado diez veces y es muy poco probable que este programador ordinario tenga que lidiar. Bueno, hasta cierto punto esto es cierto. Pero, como se vio después, no todo fue implementado, y yo, desafortunadamente (¿o afortunadamente?) Aún tenía que crear una Estructura de Datos.
Misteriosa Merkle Modificada Patricia Trie.
Como no hay información sobre este árbol en absoluto en el habr, y en el medio, un poco más, quiero decirles qué tipo de animal es y con qué se come.

Que es esto
Descargo de responsabilidad: la principal fuente de información para la implementación para mí fue el papel amarillo , así como los códigos fuente parity-ethereum y go-ethereum . Había un mínimo de información teórica sobre la justificación de ciertas decisiones, por lo que todas las conclusiones sobre las razones para tomar ciertas decisiones son personales. En caso de que me equivoque en algo, estaré encantado de hacer correcciones en los comentarios.
Un árbol es una estructura de datos que es un gráfico acíclico conectado. Aquí todo es simple, todos están familiarizados con esto.
El árbol de prefijos es el árbol raíz en el que se pueden almacenar pares clave-valor debido al hecho de que los nodos se dividen en dos tipos: aquellos que contienen parte de la ruta (prefijo) y nodos hoja que contienen el valor almacenado. Un valor está presente en un árbol si y solo si, usando la tecla, podemos ir desde la raíz del árbol y encontrar un nodo con un valor al final.
El árbol PATRICIA es un árbol de prefijos en el que los prefijos son binarios, es decir, cada nodo clave almacena información sobre un bit.
El árbol Merkle es un árbol hash construido sobre algún tipo de cadena de datos, que agrega estos mismos hash en uno (raíz), almacenando información sobre el estado de todos los bloques de datos. Es decir, el hash raíz es una especie de "firma digital" del estado de la cadena de bloques. Esta cosa se usa activamente en la cadena de bloques, y puede encontrar más información al respecto aquí .

Total: Merkle Patricia Trie modificada (en adelante MPT para abreviar) es un árbol hash que almacena pares clave-valor, y las claves se presentan en forma binaria. Y sobre qué es exactamente "Modificado", lo descubriremos un poco más tarde cuando discutamos la implementación.
¿Por qué es esto?
MPT se utiliza en el proyecto Ethereum para almacenar datos sobre cuentas, transacciones, resultados de su ejecución y otros datos necesarios para el funcionamiento del sistema.
A diferencia de Bitcoin, en el que el estado está implícito y cada nodo lo calcula de forma independiente, el saldo de cada cuenta (así como los datos asociados con él) se almacena directamente en la cadena de bloques en el aire. Además, la ubicación y la inmutabilidad de los datos deben proporcionarse criptográficamente: pocas personas usarán criptomonedas en las que el saldo de una cuenta aleatoria puede cambiar sin razones objetivas.
El principal problema que enfrentan los desarrolladores de Ethereum es la creación de una estructura de datos que pueda almacenar efectivamente pares clave-valor y al mismo tiempo proporcionar verificación de los datos almacenados. Entonces apareció MPT.
Como es eso
MPT es un árbol de prefijo PATRICIA en el que las claves son secuencias de bytes.
Los bordes de este árbol son secuencias de mordisco (medios bytes). En consecuencia, un nodo puede tener hasta dieciséis descendientes (correspondientes a ramas de 0x0 a 0xF).
Los nodos se dividen en 3 tipos:
- Nodo de rama. El nodo utilizado para ramificar. Contiene hasta 1 a 16 enlaces a nodos secundarios. También puede contener un valor.
- Nodo de extensión. Un nodo auxiliar que almacena una parte de la ruta común a varios nodos secundarios, así como un enlace al nodo de rama, que se encuentra debajo.
- Nodo de la hoja. Un nodo que contiene parte de la ruta y el valor almacenado. Es el final de la cadena.
Como ya se mencionó, MPT está construido sobre otro repositorio de kv, que almacena nodos en forma de "enlace" => "nodo codificado RLP ".
Y aquí se nos ocurre un nuevo concepto: RLP. En resumen, este es un método para codificar datos que representan listas o secuencias de bytes. Ejemplo: [ "cat", "dog" ] = [ 0xc8, 0x83, 'c', 'a', 't', 0x83, 'd', 'o', 'g' ] . No entraré en detalles en particular, y en la implementación utilizo una biblioteca preparada, ya que la cobertura de este tema también inflará un artículo ya bastante grande. Si aún está interesado, puede leer más aquí . Nos limitamos al hecho de que podemos codificar datos en RLP y volver a decodificarlos.
Un enlace a un nodo se define de la siguiente manera: si la longitud del nodo codificado RLP es de 32 o más bytes, entonces el enlace es un hash keccak de la representación RLP del nodo. Si la longitud es inferior a 32 bytes, el enlace es la representación RLP del propio nodo.
Obviamente, en el segundo caso, no necesita guardar el nodo en la base de datos, porque se guardará completamente dentro del nodo padre.

La combinación de tres tipos de nodos le permite almacenar datos de manera efectiva en el caso de que haya pocas claves (entonces la mayoría de las rutas se almacenarán en nodos de extensión y hoja, y habrá pocos nodos de ramificación), y en el caso de que haya muchos nodos (las rutas no se almacenarán explícitamente, pero se "reunirán" durante el paso a través de los nodos de las ramas).
Un ejemplo completo de un árbol que usa todo tipo de nodos:
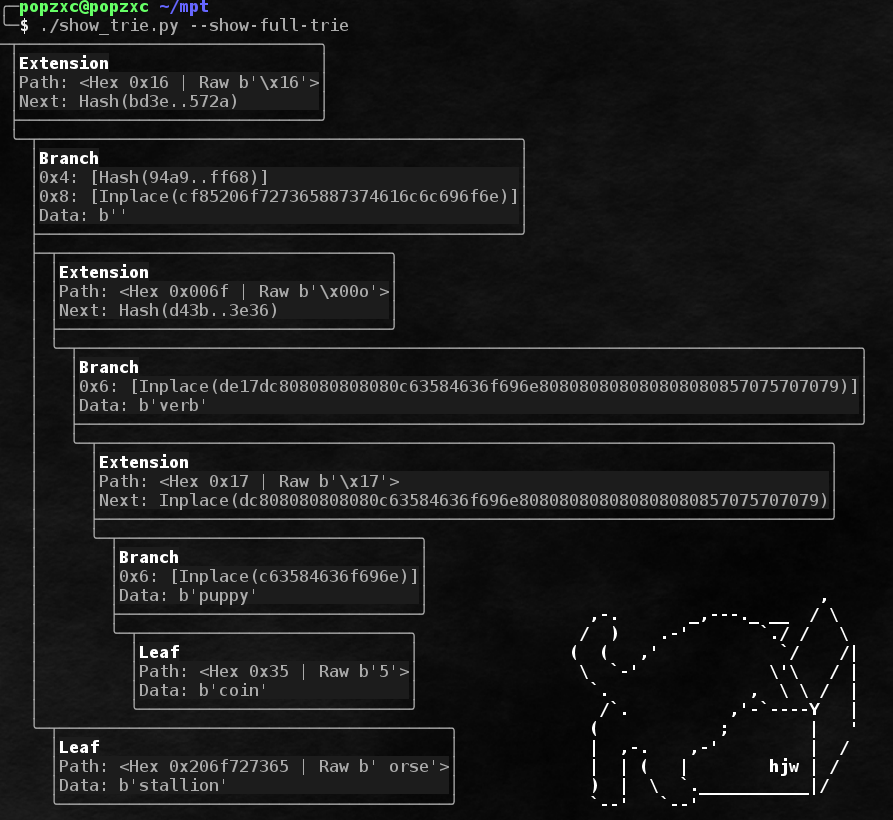
Como habrás notado, las partes almacenadas de las rutas tienen prefijos. Los prefijos son necesarios para varios propósitos:
- Distinguir los nodos de extensión de los nodos hoja.
- Para alinear secuencias de un número impar de mordiscos.
Las reglas para crear prefijos son muy simples:
- El prefijo toma 1 mordisco. Si la longitud de la ruta (excluyendo el prefijo) es impar, entonces la ruta comienza inmediatamente después del prefijo. Si la longitud de la ruta es par, para alinear después del prefijo, primero se agrega nibble 0x0.
- El prefijo es inicialmente 0x0.
- Si la longitud de la ruta es impar, entonces se agrega 0x1 al prefijo, si es par - 0x0.
- Si la ruta conduce a un nodo Hoja, se agrega 0x2 al prefijo, si se agrega 0x0 al nodo Extensión.
En beatiks, creo, será más claro:
0b0000 => , Extension 0b0001 => , Extension 0b0010 => , Leaf 0b0011 => , Leaf
Remoción que no es remoción
A pesar de que el árbol tiene la operación de eliminar nodos, de hecho, todo lo que alguna vez se agregó permanece en el árbol para siempre.
Esto es necesario para no crear un árbol completo para cada bloque, sino para almacenar solo la diferencia entre las versiones antiguas y nuevas del árbol.
En consecuencia, utilizando diferentes hashes de raíz como punto de entrada, podemos obtener cualquiera de los estados en los que el árbol ha estado.

Estas no son todas las optimizaciones. Hay más, pero no hablaremos al respecto, por lo que el artículo es amplio. Sin embargo, puedes leer por ti mismo.
Implementación
La teoría ha terminado, pasemos a la práctica. Utilizaremos lingua franca del mundo de TI, que es python .
Como habrá mucho código, y para el formato del artículo habrá que reducir y dividir mucho, dejaré inmediatamente un enlace a github .
Si es necesario, allí puede ver la imagen completa.
Primero, definimos la interfaz de árbol que queremos obtener como resultado:
class MerklePatriciaTrie: def __init__(self, storage, root=None): pass def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass
La interfaz es extremadamente simple. Las operaciones disponibles son obtener, eliminar, insertar y cambiar (combinadas en la actualización), así como obtener el hash raíz.
El almacenamiento se transferirá al método __init__ , una estructura de datos tipo dict en la que almacenaremos los nodos, así como la root , la "parte superior" del árbol. Si None se pasa None como root , asumimos que el árbol está vacío y funciona desde cero.
_Observación: es posible que se pregunte por qué las variables en los métodos se nombran como encoded_key y encoded_value , y no solo key / value . La respuesta es simple: de acuerdo con la especificación, todas las claves y valores deben estar codificados en RLP . No nos molestaremos con esto y dejaremos esta ocupación en los hombros de los usuarios de la biblioteca.
Sin embargo, antes de comenzar a implementar el árbol en sí, se deben hacer dos cosas importantes:
- Implemente la clase
NibblePath , que es una cadena de nibbles, para no codificarlos manualmente. - Para implementar la clase
Node en el marco de esta clase: Extension , Leaf y Branch .
Nibblepath
Entonces, NibblePath . Dado que nos moveremos activamente alrededor del árbol, la base de la funcionalidad de nuestra clase debería ser la capacidad de establecer el "desplazamiento" desde el comienzo de la ruta, así como recibir un mordisco específico. Sabiendo esto, definimos la base de nuestra clase (así como un par de constantes útiles para trabajar con los prefijos a continuación):
class NibblePath: ODD_FLAG = 0x10 LEAF_FLAG = 0x20 def __init__(self, data, offset=0): self._data = data
Muy simple, ¿no es así?
Queda por escribir solo funciones para codificar y decodificar una secuencia de nibbles.
class NibblePath:
En principio, este es el mínimo necesario para un trabajo conveniente con mordiscos. Por supuesto, en la implementación actual todavía hay una serie de métodos auxiliares (como combine , fusionar dos caminos en uno), pero su implementación es muy trivial. Si está interesado, la versión completa se puede encontrar aquí .
Nodo
Como ya sabemos, nuestros nodos se dividen en tres tipos: Hoja, Extensión y Rama. Todos ellos pueden codificarse y decodificarse, y la única diferencia son los datos que se almacenan en su interior. Para ser sincero, esto es lo que se piden los tipos de datos algebraicos, y en Rust , por ejemplo, escribiría algo en el espíritu:
pub enum Node<'a> { Leaf(NibblesSlice<'a>, &'a [u8]), Extension(NibblesSlice<'a>, NodeReference), Branch([Option<NodeReference>; 16], Option<&'a [u8]>), }
Sin embargo, no hay ADT en Python como tal, por lo que definiremos la clase Node , y dentro de ella hay tres clases correspondientes a los tipos de nodos. Implementamos la codificación directamente en las clases de nodo y la decodificación en la clase de Node .
La implementación, sin embargo, es elemental:
Hoja:
class Leaf: def __init__(self, path, data): self.path = path self.data = data def encode(self):
Extensión:
class Extension: def __init__(self, path, next_ref): self.path = path self.next_ref = next_ref def encode(self):
Rama:
class Branch: def __init__(self, branches, data=None): self.branches = branches self.data = data def encode(self):
Todo es muy sencillo. Lo único que puede causar preguntas es la función _prepare_reference_for_encoding .
Entonces confieso, tuve que usar una muleta pequeña. El hecho es que la biblioteca rlp decodifica los datos de forma recursiva, y el enlace a otro nodo, como sabemos, puede ser datos rlp (en caso de que el nodo codificado tenga menos de 32 caracteres). Trabajar con enlaces en dos formatos (bytes hash y un nodo descodificado) es muy inconveniente. Por lo tanto, escribí dos funciones que, después de decodificar el nodo, devuelven los enlaces en formato de bytes y los decodifican si es necesario, antes de guardarlos. Estas funciones son:
def _prepare_reference_for_encoding(ref):
Termine con nodos escribiendo una clase Node . Solo habrá 2 métodos: decodificar el nodo y convertir el nodo en un enlace.
class Node:
Un descanso
Fuh! Hay mucha información Creo que es hora de relajarse. Aquí hay otro gato para ti:
Milota, verdad? Bien, de vuelta a nuestros árboles.
MerklePatriciaTrie
Hurra: los elementos auxiliares están listos, pasamos a los más deliciosos. Por si acaso, recordaré la interfaz de nuestro árbol. Al mismo tiempo, implementamos el método __init__ .
class MerklePatriciaTrie: def __init__(self, storage, root=None): self._storage = storage self._root = root def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass
Pero con los métodos restantes trataremos uno por uno.
obtener
El método get (como, en principio, los otros métodos) constará de dos partes. El método mismo preparará los datos y traerá el resultado a la forma esperada, mientras que el trabajo real ocurrirá dentro del método auxiliar.
El método básico es extremadamente simple:
class MerklePatriciaTrie:
Sin embargo, _get no _get mucho más complicado: para llegar al nodo deseado, necesitamos ir desde la raíz a la ruta completa. Si al final encontramos un nodo con datos (Hoja o Rama) - hurra, los datos se reciben. Si no fue posible pasar, falta la clave requerida en el árbol.
Implementación
class MerklePatriciaTrie:
Bueno, al mismo tiempo, escribiremos métodos para guardar y cargar nodos. Son simples:
class MerklePatriciaTrie:
actualizar
El método de update ya es más interesante. Simplemente vaya hasta el final e inserte el nodo Hoja no siempre funcionará. Es probable que el punto de separación clave esté en algún lugar dentro del nodo Hoja o Extensión ya guardado. En este caso, tendrá que separarlos y crear varios nodos nuevos.
En general, toda la lógica se puede describir mediante las siguientes reglas:
- Si bien el camino coincide por completo con los nodos existentes, descendemos recursivamente del árbol.
- Si la ruta está terminada y estamos en el nodo Rama u Hoja, significa que la
update simplemente actualiza el valor correspondiente a esta clave. - Si las rutas están divididas (es decir, no actualizamos el valor, pero insertamos uno nuevo), y estamos en el nodo Rama, creamos un nodo Hoja y le especificamos un enlace en la rama correspondiente.
- Si las rutas están divididas y estamos en un nodo Hoja o Extensión, necesitamos crear un nodo Rama que separe las rutas y, si es necesario, un nodo Extensión para la parte común de la ruta.
Expresemos esto gradualmente en código. ¿Por qué gradualmente? Debido a que el método es grande y será difícil de entender a granel.
Sin embargo, dejaré un enlace al método completo aquí .
class MerklePatriciaTrie:
No hay suficiente lógica general, todo lo más interesante está adentro if s.
if type(node) == Node.Leaf
Primero, tratemos con los nodos Leaf. Solo son posibles 2 escenarios con ellos:
El resto del camino que estamos siguiendo es exactamente el mismo que el camino almacenado en el nodo Hoja. En este caso, solo necesitamos cambiar el valor, guardar el nuevo nodo y devolverle un enlace.
Los caminos son diferentes.
En este caso, debe crear un nodo Branch que separe las dos rutas.
Si una de las rutas está vacía, su valor se transferirá directamente al nodo Branch.
De lo contrario, tendremos que crear dos nodos Leaf acortados por la longitud de la parte común de las rutas + 1 mordisco (este mordisco se indicará mediante el índice de la rama correspondiente del nodo Branch).
También deberá verificar si hay una parte común de la ruta para comprender si también necesitamos crear un nodo de Extensión.
En el código, se verá así:
if type(node) == Node.Leaf: if node.path == path:
El procedimiento _create_branch_node es el siguiente:
def _create_branch_node(self, path_a, value_a, path_b, value_b):
if type(node) == Node.Extension
En el caso del nodo Extensión, todo parece un nodo Hoja.
Si la ruta desde el nodo de Extensión es un prefijo para nuestra ruta, simplemente avanzamos recursivamente.
De lo contrario, necesitamos hacer la separación usando el nodo Branch, como en el caso descrito anteriormente.
En consecuencia, el código:
elif type(node) == Node.Extension: if path.starts_with(node.path):
El procedimiento _create_branch_extension lógicamente equivalente al procedimiento _create_branch_leaf , pero funciona con el nodo Extension.
if type(node) == Node.Branch
Pero con el nodo Branch, todo es simple. Si la ruta está vacía, simplemente guardamos el nuevo valor en el nodo Branch actual. Si el camino no está vacío, "mordimos" un mordisco de él y recursivamente bajamos.
El código, creo, no necesita comentarios.
elif type(node) == Node.Branch: if len(path) == 0: return self._store_node(Node.Branch(node.branches, value)) idx = path.at(0) new_reference = self._update(node.branches[idx], path.consume(1), value) node.branches[idx] = new_reference return self._store_node(node)
eliminar
Fuh! El último método permanece. El es el más alegre. La complejidad de la eliminación es que necesitamos devolver la estructura al estado en el que habría caído si hubiéramos hecho toda la cadena de update , excluyendo solo la clave eliminada.
, , , , . "", , .
. , N- , N+1 . enum — DeleteAction , .
delete :
class MerklePatriciaTrie:
, get update . . .
if type(node) == Node.Leaf
. . — , , .
:
if type(node) == Node.Leaf: if path == node.path: return MerklePatriciaTrie._DeleteAction.DELETED, None else: raise KeyError
, "" — . , . .
if type(node) == Node.Extension
C Extension- :
- , Extension- . — .
_delete , "" .- . :
- . .
- . .
- Branch-. . , Branch- . , , Leaf-. — Extension-.
:
elif type(node) == Node.Extension: if not path.starts_with(node.path): raise KeyError
if type(node) == Node.Branch
.
, . Branch-, …
Por qué Branch- Leaf- ( ) Extension- ( ).
, . , — Leaf-. — Extension-. , , 2 — Branch- .
? :
:
- , .
- ,
_delete .
:
elif type(node) == Node.Branch: action = None idx = None info = None if len(path) == 0 and len(node.data) == 0: raise KeyError elif len(path) == 0 and len(node.data) != 0: node.data = b'' action = MerklePatriciaTrie._DeleteAction.DELETED else:
_DeleteAction .
- Branch- , ( , ). .
if action == MerklePatriciaTrie._DeleteAction.UPDATED:
- ( , ), , .
. :
- . , , , . , .
- , . Leaf- . .
- , . , , .
- , , Branch- . ,
_DeleteAction — UPDATED .
if action == MerklePatriciaTrie._DeleteAction.DELETED: non_empty_count = sum(map(lambda x: 1 if len(x) > 0 else 0, node.branches)) if non_empty_count == 0 and len(node.data) == 0:
_build_new_node_from_last_branch .
— Leaf Extension, , .
— Branch, Extension , , Branch.
def _build_new_node_from_last_branch(self, branches):
El resto
. , … root .
Aquí:
class MerklePatriciaTrie:
, .
… . , , Ethereum . , , , . , :)
, , pip install -U eth_mpt — .

Resultados
?
, -, , - , , . — , .
-, , , — . , skip list interval tree, — , , .
-, , . , - .
-, — .
, , — !
: 1 , 2 , 3 . ! , .