Ya hemos discutido el motor de indexación de PostgreSQL, la interfaz de los métodos de acceso y tres métodos: índice hash , árbol B y GiST . En este artículo, describiremos SP-GiST.

SP-GiST

Primero, algunas palabras sobre este nombre. La parte "GiST" alude a alguna similitud con el método de acceso con el mismo nombre. La similitud existe: ambos son árboles de búsqueda generalizados que proporcionan un marco para construir varios métodos de acceso.

"SP" significa partición del espacio. El espacio aquí es a menudo justo lo que estamos acostumbrados a llamar un espacio, por ejemplo, un plano bidimensional. Pero veremos que se entiende cualquier espacio de búsqueda, es decir, en realidad cualquier dominio de valor.

SP-GiST es adecuado para estructuras donde el espacio se puede dividir recursivamente en áreas que no se cruzan . Esta clase comprende cuadrúteros, árboles k-dimensionales (árboles kD) y árboles radix.

Estructura

Entonces, la idea del método de acceso SP-GiST es dividir el dominio de valor en subdominios no superpuestos, cada uno de los cuales, a su vez, también se puede dividir. Particionar de esta manera induce árboles no balanceados (a diferencia de los árboles B y GiST regular).

El rasgo de no intersectarse simplifica la toma de decisiones durante la inserción y la búsqueda. Por otro lado, como regla, los árboles inducidos son de baja ramificación. Por ejemplo, un nodo de un quadtree generalmente tiene cuatro nodos secundarios (a diferencia de los árboles B, donde los nodos ascienden a cientos) y una profundidad mayor. Los árboles como estos se adaptan bien al trabajo en RAM, pero el índice se almacena en un disco y, por lo tanto, para reducir el número de operaciones de E / S, los nodos deben estar empaquetados en páginas, y no es fácil hacerlo de manera eficiente. Además, el tiempo que lleva encontrar diferentes valores en el índice puede variar debido a las diferencias en las profundidades de las ramas.

Este método de acceso, al igual que GiST, se encarga de tareas de bajo nivel (acceso simultáneo y bloqueos, registro y un algoritmo de búsqueda puro) y proporciona una interfaz simplificada especializada para permitir agregar soporte para nuevos tipos de datos y nuevos algoritmos de partición.

Un nodo interno del árbol SP-GiST almacena referencias a nodos secundarios; Se puede definir una etiqueta para cada referencia. Además, un nodo interno puede almacenar un valor llamado prefijo . En realidad, este valor no es obligatorio un prefijo; se puede considerar como un predicado arbitrario que se cumple para todos los nodos secundarios.

Los nodos hoja de SP-GiST contienen un valor del tipo indexado y una referencia a una fila de tabla (TID). Los datos indexados en sí (clave de búsqueda) se pueden usar como valor, pero no son obligatorios: se puede almacenar un valor acortado.

Además, los nodos hoja se pueden agrupar en listas. Por lo tanto, un nodo interno puede hacer referencia no solo a un valor, sino a una lista completa.

Tenga en cuenta que los prefijos, las etiquetas y los valores en los nodos hoja tienen sus propios tipos de datos, independientes entre sí.

De la misma manera que en GiST, la función principal para definir para la búsqueda es la función de coherencia . Esta función se llama para un nodo de árbol y devuelve un conjunto de nodos secundarios cuyos valores "son consistentes" con el predicado de búsqueda (como de costumbre, en la forma " expresión de operador de campo indexado "). Para un nodo hoja, la función de coherencia determina si el valor indexado en este nodo cumple con el predicado de búsqueda.

La búsqueda comienza con el nodo raíz. La función de coherencia permite descubrir qué nodos secundarios tiene sentido visitar. El algoritmo se repite para cada uno de los nodos encontrados. La búsqueda es profunda primero.

A nivel físico, los nodos de índice se agrupan en páginas para que el trabajo con los nodos sea eficiente desde el punto de vista de las operaciones de E / S. Tenga en cuenta que una página puede contener nodos internos o nodales, pero no ambos.

Ejemplo: quadtree

Un quadtree se usa para indexar puntos en un plano. Una idea es dividir recursivamente áreas en cuatro partes (cuadrantes) con respecto al punto central . La profundidad de las ramas en dicho árbol puede variar y depende de la densidad de los puntos en los cuadrantes apropiados.

Así es como se ve en las cifras, por ejemplo de la base de datos de demostración aumentada por aeropuertos desde el sitio openflights.org . Por cierto, recientemente lanzamos una nueva versión de la base de datos en la que, entre el resto, reemplazamos longitud y latitud con un campo de tipo "punto".


Primero, dividimos el avión en cuatro cuadrantes ...


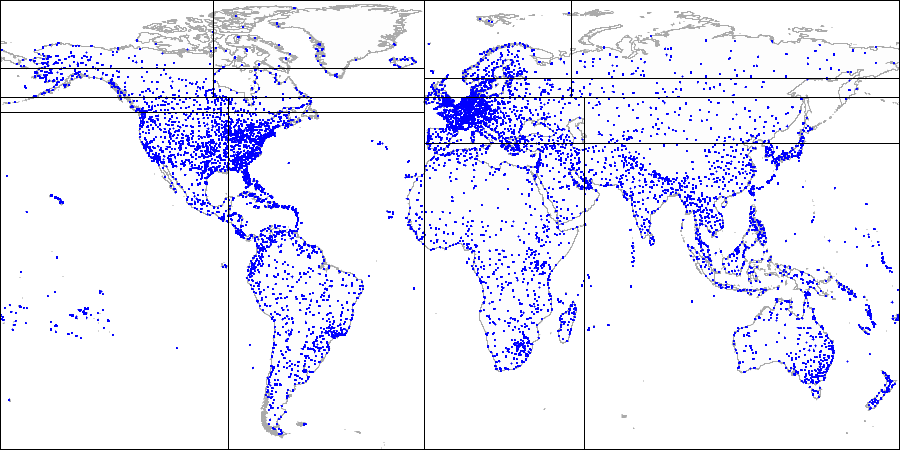Luego dividimos cada uno de los cuadrantes ...


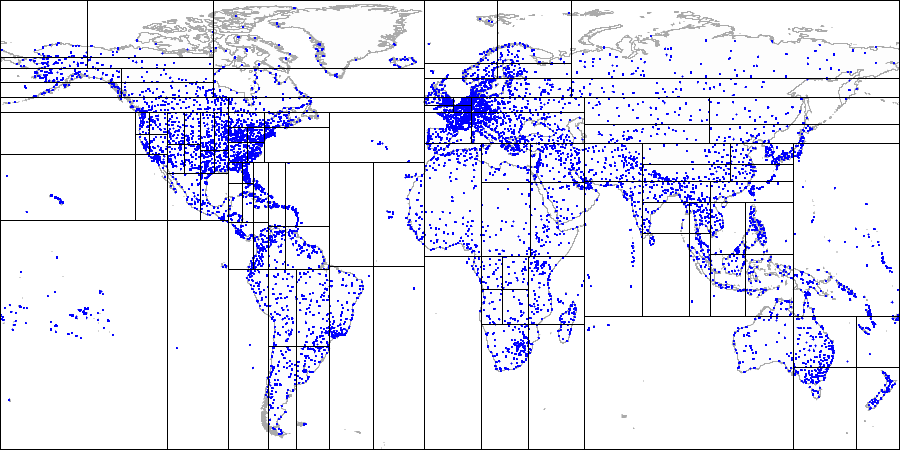Y así sucesivamente hasta que obtengamos la partición final.

Proporcionemos más detalles de un ejemplo simple que ya consideramos en el artículo relacionado con GiST . Vea cómo se verá la partición en este caso:



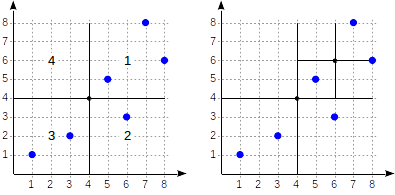
Los cuadrantes están numerados como se muestra en la primera figura. En aras de la definición, ubiquemos los nodos secundarios de izquierda a derecha exactamente en la misma secuencia. Una posible estructura de índice en este caso se muestra en la figura a continuación. Cada nodo interno hace referencia a un máximo de cuatro nodos secundarios. Cada referencia se puede etiquetar con el número del cuadrante, como en la figura. Pero no hay una etiqueta en la implementación, ya que es más conveniente almacenar una matriz fija de cuatro referencias, algunas de las cuales pueden estar vacías.



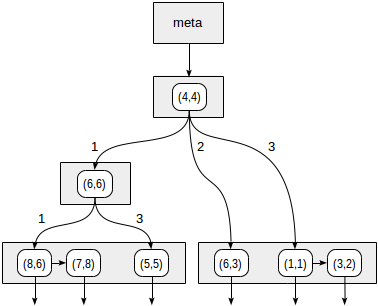
Los puntos que se encuentran en los límites se relacionan con el cuadrante con el número más pequeño.

postgres=# create table points(p point); postgres=# insert into points(p) values (point '(1,1)'), (point '(3,2)'), (point '(6,3)'), (point '(5,5)'), (point '(7,8)'), (point '(8,6)'); postgres=# create index points_quad_idx on points using spgist(p); 

En este caso, la clase de operador "quad_point_ops" se usa por defecto, que contiene los siguientes operadores:

 postgres=# select amop.amopopr::regoperator, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'quad_point_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'spgist' and amop.amoplefttype = opc.opcintype; 

  amopopr | amopstrategy -----------------+-------------- <<(point,point) | 1 strictly left >>(point,point) | 5 strictly right ~=(point,point) | 6 coincides <^(point,point) | 10 strictly below >^(point,point) | 11 strictly above <@(point,box) | 8 contained in rectangle (6 rows) 

Por ejemplo, veamos cómo la consulta select * from points where p >^ point '(2,7)' (encuentre todos los puntos que se encuentran por encima del dado).



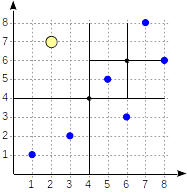
Comenzamos con el nodo raíz y usamos la función de consistencia para seleccionar a qué nodos secundarios descender. Para el operador >^ , esta función compara el punto (2,7) con el punto central del nodo (4,4) y selecciona los cuadrantes que pueden contener los puntos buscados, en este caso, los cuadrantes primero y cuarto.

En el nodo correspondiente al primer cuadrante, nuevamente determinamos los nodos secundarios utilizando la función de consistencia. El punto central es (6,6), y nuevamente necesitamos mirar a través del primer y cuarto cuadrantes.



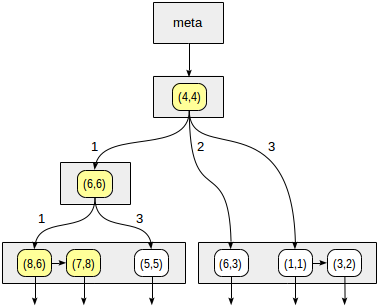
La lista de nodos hoja (8.6) y (7.8) corresponde al primer cuadrante, del cual solo el punto (7.8) cumple la condición de consulta. La referencia al cuarto cuadrante está vacía.

En el nodo interno (4.4), la referencia al cuarto cuadrante también está vacía, lo que completa la búsqueda.

 postgres=# set enable_seqscan = off; postgres=# explain (costs off) select * from points where p >^ point '(2,7)'; 

  QUERY PLAN ------------------------------------------------ Index Only Scan using points_quad_idx on points Index Cond: (p >^ '(2,7)'::point) (2 rows) 

Internos

Podemos explorar la estructura interna de los índices SP-GiST utilizando la extensión " gevel ", que se mencionó anteriormente. La mala noticia es que, debido a un error, esta extensión funciona incorrectamente con las versiones modernas de PostgreSQL. La buena noticia es que planeamos aumentar "pageinspect" con la funcionalidad de "gevel" ( discusión ). Y el error ya se ha solucionado en "pageinspect".

Una vez más, las malas noticias son que el parche se ha quedado sin progreso.

Por ejemplo, tomemos la base de datos de demostración extendida, que se usó para dibujar imágenes con el mapa mundial.

 demo=# create index airports_coordinates_quad_idx on airports_ml using spgist(coordinates); 

Primero, podemos obtener algunas estadísticas para el índice:

 demo=# select * from spgist_stats('airports_coordinates_quad_idx'); 

  spgist_stats ---------------------------------- totalPages: 33 + deletedPages: 0 + innerPages: 3 + leafPages: 30 + emptyPages: 2 + usedSpace: 201.53 kbytes+ usedInnerSpace: 2.17 kbytes + usedLeafSpace: 199.36 kbytes+ freeSpace: 61.44 kbytes + fillRatio: 76.64% + leafTuples: 5993 + innerTuples: 37 + innerAllTheSame: 0 + leafPlaceholders: 725 + innerPlaceholders: 0 + leafRedirects: 0 + innerRedirects: 0 (1 row) 

Y segundo, podemos generar el árbol de índice en sí:

 demo=# select tid, n, level, tid_ptr, prefix, leaf_value from spgist_print('airports_coordinates_quad_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix point, -- prefix type node_label int, -- label type (unused here) leaf_value point -- list value type ) order by tid, n; 

  tid | n | level | tid_ptr | prefix | leaf_value ---------+---+-------+---------+------------------+------------------ (1,1) | 0 | 1 | (5,3) | (-10.220,53.588) | (1,1) | 1 | 1 | (5,2) | (-10.220,53.588) | (1,1) | 2 | 1 | (5,1) | (-10.220,53.588) | (1,1) | 3 | 1 | (5,14) | (-10.220,53.588) | (3,68) | | 3 | | | (86.107,55.270) (3,70) | | 3 | | | (129.771,62.093) (3,85) | | 4 | | | (57.684,-20.430) (3,122) | | 4 | | | (107.438,51.808) (3,154) | | 3 | | | (-51.678,64.191) (5,1) | 0 | 2 | (24,27) | (-88.680,48.638) | (5,1) | 1 | 2 | (5,7) | (-88.680,48.638) | ... 

Pero tenga en cuenta que "spgist_print" genera no todos los valores de hoja, sino solo el primero de la lista, y por lo tanto muestra la estructura del índice en lugar de su contenido completo.

Ejemplo: árboles k-dimensionales

Para los mismos puntos en el plano, también podemos sugerir otra forma de particionar el espacio.

Dibujemos una línea horizontal a través del primer punto que se indexa. Se divide el avión en dos partes: superior e inferior. El segundo punto a indexar cae en una de estas partes. A través de este punto, dibujemos una línea vertical , que divide esta parte en dos: derecha e izquierda. Nuevamente dibujamos una línea horizontal a través del siguiente punto y una línea vertical a través del siguiente punto, y así sucesivamente.

Todos los nodos internos del árbol construido de esta manera tendrán solo dos nodos secundarios. Cada una de las dos referencias puede conducir al nodo interno que sigue en la jerarquía o a la lista de nodos hoja.

Este método puede generalizarse fácilmente para espacios k-dimensionales y, por lo tanto, los árboles también se denominan k-dimensionales (árboles kD) en la literatura.

Explicando el método por ejemplo de aeropuertos:


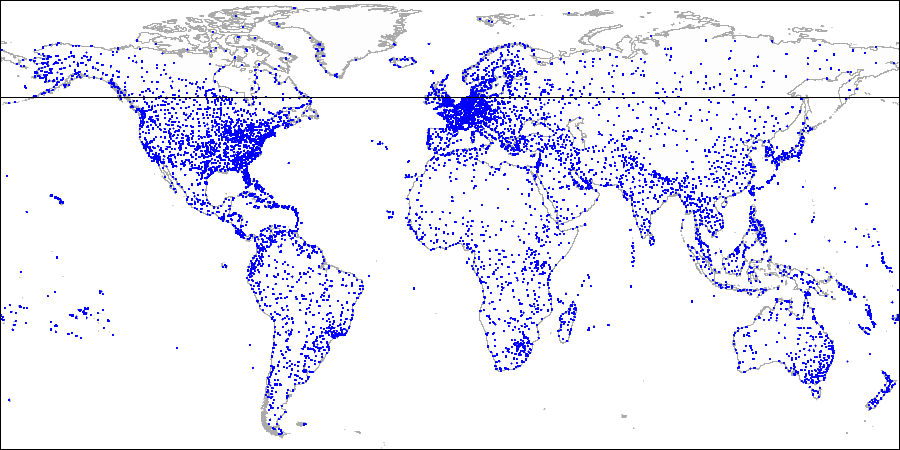Primero dividimos el avión en partes superior e inferior ...


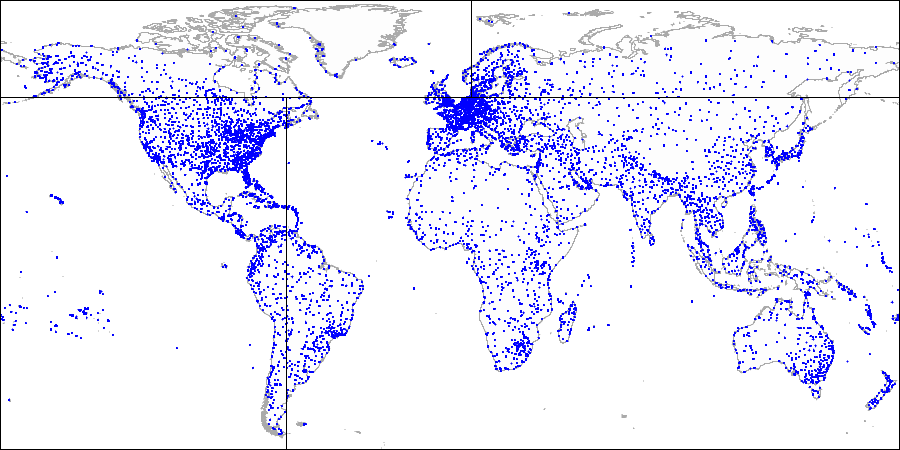Luego dividimos cada parte en partes izquierda y derecha ...


Y así sucesivamente hasta que obtengamos la partición final.

Para utilizar una partición como esta, debemos especificar explícitamente la clase de operador "kd_point_ops" al crear un índice.

 postgres=# create index points_kd_idx on points using spgist(p kd_point_ops); 

Esta clase incluye exactamente los mismos operadores que la clase "predeterminada" "quad_point_ops".

Internos

Al mirar a través de la estructura de árbol, debemos tener en cuenta que el prefijo en este caso es solo una coordenada en lugar de un punto:

 demo=# select tid, n, level, tid_ptr, prefix, leaf_value from spgist_print('airports_coordinates_kd_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix float, -- prefix type node_label int, -- label type (unused here) leaf_value point -- list node type ) order by tid, n; 

  tid | n | level | tid_ptr | prefix | leaf_value ---------+---+-------+---------+------------+------------------ (1,1) | 0 | 1 | (5,1) | 53.740 | (1,1) | 1 | 1 | (5,4) | 53.740 | (3,113) | | 6 | | | (-7.277,62.064) (3,114) | | 6 | | | (-85.033,73.006) (5,1) | 0 | 2 | (5,12) | -65.449 | (5,1) | 1 | 2 | (5,2) | -65.449 | (5,2) | 0 | 3 | (5,6) | 35.624 | (5,2) | 1 | 3 | (5,3) | 35.624 | ... 

Ejemplo: árbol radix

También podemos usar SP-GiST para implementar un árbol de radix para cadenas. La idea de un árbol de radix es que una cadena a indexar no se almacena completamente en un nodo hoja, sino que se obtiene concatenando los valores almacenados en los nodos por encima de este hasta la raíz.

Supongamos que necesitamos indexar las URL del sitio: "postgrespro.ru", "postgrespro.com", "postgresql.org" y "planet.postgresql.org".

 postgres=# create table sites(url text); postgres=# insert into sites values ('postgrespro.ru'),('postgrespro.com'),('postgresql.org'),('planet.postgresql.org'); postgres=# create index on sites using spgist(url); 

El árbol se verá de la siguiente manera:



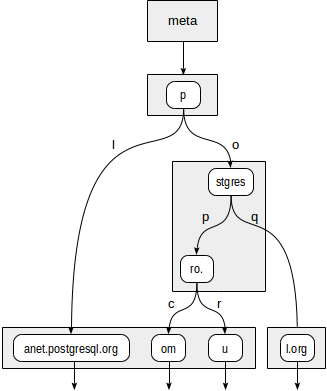
Los nodos internos del árbol almacenan prefijos comunes a todos los nodos secundarios. Por ejemplo, en los nodos secundarios de "stgres", los valores comienzan con "p" + "o" + "stgres".

A diferencia de los quadtrees, cada puntero a un nodo secundario se etiqueta adicionalmente con un carácter (más exactamente, con dos bytes, pero esto no es tan importante).

La clase de operador "Text_ops" admite operadores tipo árbol B: "igual", "mayor" y "menor":

 postgres=# select amop.amopopr::regoperator, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'text_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'spgist' and amop.amoplefttype = opc.opcintype; 

  amopopr | amopstrategy -----------------+-------------- ~<~(text,text) | 1 ~<=~(text,text) | 2 =(text,text) | 3 ~>=~(text,text) | 4 ~>~(text,text) | 5 <(text,text) | 11 <=(text,text) | 12 >=(text,text) | 14 >(text,text) | 15 (9 rows) 

La distinción de los operadores con tildes es que manipulan bytes en lugar de caracteres .

A veces, una representación en forma de árbol de radix puede resultar mucho más compacta que el árbol B ya que los valores no se almacenan completamente, sino que se reconstruyen a medida que surge la necesidad al descender a través del árbol.

Considere una consulta: select * from sites where url like 'postgresp%ru' . Se puede realizar utilizando el índice:

 postgres=# explain (costs off) select * from sites where url like 'postgresp%ru'; 

  QUERY PLAN ------------------------------------------------------------------------------ Index Only Scan using sites_url_idx on sites Index Cond: ((url ~>=~ 'postgresp'::text) AND (url ~<~ 'postgresq'::text)) Filter: (url ~~ 'postgresp%ru'::text) (3 rows) 

En realidad, el índice se usa para buscar valores que sean mayores o iguales a "postgresp", pero menores que "postgresq" (Índice Cond), y luego se eligen los valores coincidentes del resultado (Filtro).

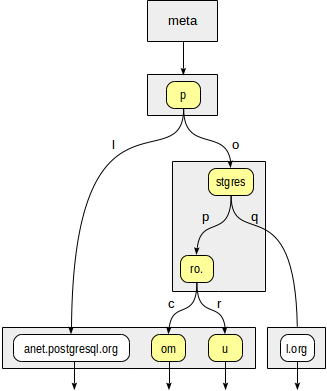
Primero, la función de consistencia debe decidir a qué nodos hijos de la raíz "p" necesitamos descender. Hay dos opciones disponibles: "p" + "l" (no es necesario descender, lo que está claro incluso sin sumergirse más profundo) y "p" + "o" + "stgres" (continuar el descenso).

Para el nodo "stgres", se necesita nuevamente una llamada a la función de coherencia para verificar "postgres" + "p" + "ro". (continuar el descenso) y "postgres" + "q" (no es necesario descender).

Para "ro". nodo y todos sus nodos hoja secundarios, la función de coherencia responderá "sí", por lo que el método de índice devolverá dos valores: "postgrespro.com" y "postgrespro.ru". Se seleccionará un valor coincidente de ellos en la etapa de filtrado.

Internos

Al mirar a través de la estructura de árbol, debemos tener en cuenta los tipos de datos:

 postgres=# select * from spgist_print('sites_url_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix text, -- prefix type node_label smallint, -- label type leaf_value text -- leaf node type ) order by tid, n; 

Propiedades

Veamos las propiedades del método de acceso SP-GiST (las consultas se proporcionaron anteriormente ):

  amname | name | pg_indexam_has_property --------+---------------+------------------------- spgist | can_order | f spgist | can_unique | f spgist | can_multi_col | f spgist | can_exclude | t 

Los índices SP-GiST no se pueden usar para ordenar y para soportar la restricción única. Además, índices como este no se pueden crear en varias columnas (a diferencia de GiST). Pero está permitido usar dichos índices para admitir restricciones de exclusión.

Las siguientes propiedades de capa de índice están disponibles:

  name | pg_index_has_property ---------------+----------------------- clusterable | f index_scan | t bitmap_scan | t backward_scan | f 

La diferencia con GiST aquí es que la agrupación es imposible.

Y, finalmente, las siguientes son propiedades de capa de columna:

  name | pg_index_column_has_property --------------------+------------------------------ asc | f desc | f nulls_first | f nulls_last | f orderable | f distance_orderable | f returnable | t search_array | f search_nulls | t 

La clasificación no es compatible, lo cual es predecible. Los operadores de distancia para la búsqueda de vecinos más cercanos no están disponibles en SP-GiST hasta el momento. Lo más probable es que esta característica sea compatible en el futuro.

Es compatible con el próximo PostgreSQL 12, el parche de Nikita Glukhov.

SP-GiST se puede usar para escaneo de solo índice, al menos para las clases de operador discutidas. Como hemos visto, en algunos casos, los valores indexados se almacenan explícitamente en nodos de hoja, mientras que en los otros, los valores se reconstruyen parte por parte durante el descenso del árbol.

Nulos

Para no complicar la imagen, no hemos mencionado NULL hasta ahora. De las propiedades del índice se desprende que los NULL son compatibles. De verdad:

 postgres=# explain (costs off) select * from sites where url is null; 

  QUERY PLAN ---------------------------------------------- Index Only Scan using sites_url_idx on sites Index Cond: (url IS NULL) (2 rows) 

Sin embargo, NULL es algo extraño para SP-GiST. Todos los operadores de la clase de operador "spgist" deben ser estrictos: un operador debe devolver NULL siempre que cualquiera de sus parámetros sea NULL. El método en sí mismo asegura esto: los NULL simplemente no se pasan a los operadores.

Pero para usar el método de acceso para la exploración de solo índice, los NULL deben almacenarse en el índice de todos modos. Y se almacenan, pero en un árbol separado con su propia raíz.

Otros tipos de datos

Además de los árboles de puntos y radix para cadenas, también se implementan otros métodos basados ​​en SP-GiST PostgreSQL:

• La clase de operador Box_ops proporciona un quadtree para rectángulos.
  Cada rectángulo está representado por un punto en un espacio de cuatro dimensiones , por lo que el número de cuadrantes es igual a 16. Un índice como este puede vencer a GiST en el rendimiento cuando hay muchas intersecciones de los rectángulos: en GiST es imposible dibujar límites para separar los objetos que se cruzan entre sí, mientras que no hay tales problemas con los puntos (incluso en cuatro dimensiones).
  
• La clase de operador "Range_ops" proporciona un quadtree para intervalos.
  Un intervalo está representado por un punto bidimensional : el límite inferior se convierte en la abscisa y el límite superior se convierte en la ordenada.
  

Sigue leyendo .