🕓 🔔 🥝 Modelamos el algoritmo MUSIC para determinar la dirección de llegada de una onda electromagnética 🧝 😝 👩🏾‍🤝‍👩🏻

aaspcats

Prólogo

Comenzaré mi presentación desde lejos. Érase una vez, en el lejano 2016-2017, su humilde servidor logró ir a un curso de capacitación de seis meses a la lejana ciudad de Ilmenau (Alemania), donde completó con éxito (en general) el programa de maestría de Procesamiento de comunicaciones y señales . El programa no fue fácil, pero ahora es incluso agradable recordarlo. A veces ...

Entonces, al final de esta capacitación, además del diploma, todavía tenía algunos materiales diferentes en mis manos, que pensé que era incorrecto no compartir.

Uno de estos materiales está frente a ti.

¿Qué objetivos perseguí mientras preparaba el seminario ?

hablar sobre algunos enfoques "inteligentes" ya establecidos en el tema de los conjuntos de antenas más accesibles y hacerlo en ruso;
realice una pequeña simulación en Python 3 para agitar a otros ingenieros de radio para que echen un vistazo más de cerca a los lenguajes de programación (si aún no lo ha examinado de cerca);
proporcionar enlaces a buena literatura en inglés, sin leer fuentes extranjeras, ahora, por desgracia, en ninguna parte.

Que considerar :

El método MUSIC (clasificación múltiple múltiple): esto, de hecho, se refiere a la vista previa.

Puede encontrar un ejemplo de formación de gráficos y el método MVDR aquí (si hay preguntas o sugerencias para material adicional, la discusión puede continuar en Github.Gist).

Como dije anteriormente, usaremos Python, a saber:

import numpy as np import matplotlib.pyplot as plt

¿Por qué no MATLAB, uno de los candidatos más populares y convenientes para el modelado de álgebra lineal? Porque quiero mostrar que se puede hacer un trabajo similar en Python, y el alcance de Python es mucho más amplio que el de MATLAB. Por lo tanto, estar familiarizado con la sintaxis de Python es algo útil, en mi opinión.

¡Empecemos!

Las fórmulas se preparan a través de https://upmath.me/ . ¡Gracias a los creadores por una gran herramienta!

Declaración del problema.

Supongamos que hay un conjunto de antenas lineales que consta de una serie de elementos separados entre sí $\ Delta = \ frac {\ lambda} {2}$ (paso del conjunto de antenas), donde $\ lambda$ - la longitud de la onda portadora electromagnética (EM).

Las ondas electromagnéticas caen sobre este conjunto de antenas desde diferentes direcciones.

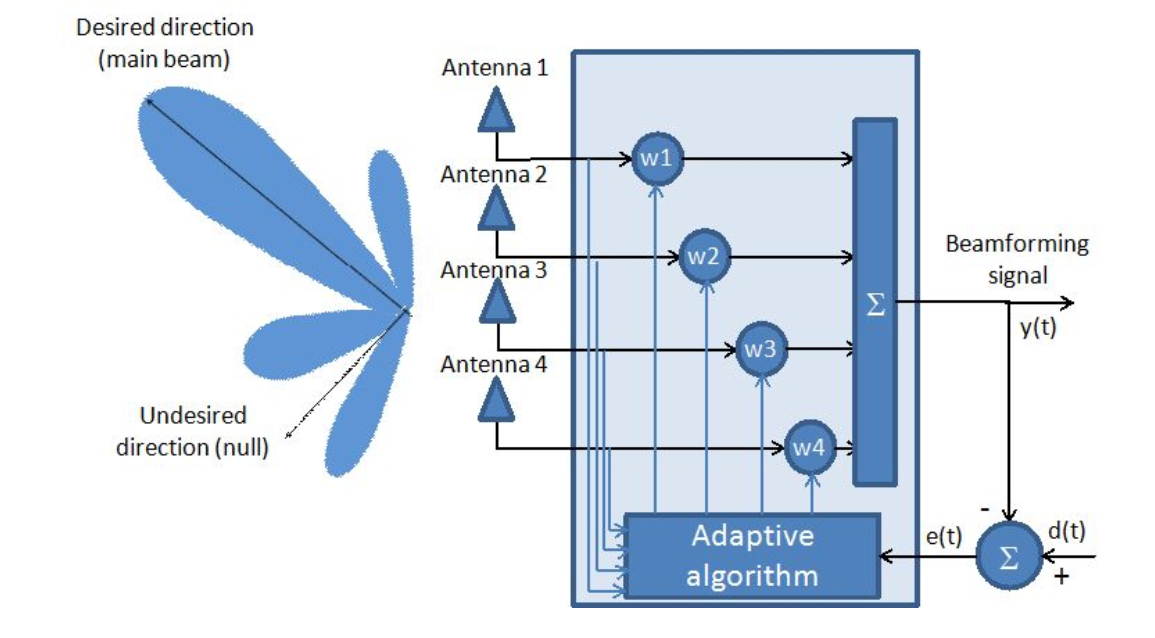
Fig. 1. Sistema de antena adaptable.

Como se puede ver en la figura, el conjunto de antenas se considera como un filtro adaptativo.

En realidad, encontrar el vector óptimo de coeficientes ( $\ mathbf {w} _ {opt}$ ) es la tarea principal de las matrices de antenas adaptativas desde un punto de vista matemático.

Inicialmente, no sabemos de qué direcciones particulares provienen las señales y cuántas de ellas. Para resolver esta contradicción usaremos el algoritmo MUSIC, un algoritmo para estimar frecuencias espaciales con alta resolución.

Simulación de señal recibida

Podemos presentar el modelo de la señal recibida a través de la fórmula:

$\ mathbf {X} = \ mathbf {A} \ mathbf {S} + \ mathbf {N}$

donde $\ mathbf {A} = [\ mathbf {a} (\ theta_1) \ quad \ mathbf {a} (\ theta_2) \ quad ... \ quad \ mathbf {a} (\ theta_d)]$ - matriz de vectores de exploración (vectores de dirección) del conjunto de antenas ( $a_i = \ exp (-j \ mu m_i)$ , $m = 0, 1 ... (M-1)$ , $M$ - el número de elementos del conjunto de antenas, $d$ - el número de fuentes de ondas EM, $\ theta$ - ángulo de la dirección de llegada de la onda EM), $\ mathbf {S}$ - matriz de caracteres transmitidos, y $\ mathbf {N}$ - matriz de ruido aditivo.

Fig. 2. Conjunto de antenas lineales omnidireccionales (ULAA - conjunto de antenas lineal uniforme) [1, p. 32]

Replanteemos esta fórmula de la manera "cotidiana": en nuestra cuadrícula obtenemos algo de "desorden" a partir de varias señales, que denotamos por $\ mathbf {X}$ . No recibimos explícitamente información sobre el número de fuentes y direcciones, sin embargo, la información sobre esto está contenida en la señal recibida.

Estamos empezando a buscar!

Para hacer esto, generalmente proceden a manipulaciones no con las matrices de amplitudes de señal complejas, sino con sus covarianzas (es decir, en esencia, con poderes):

$\ mathbf {R} _ {xx} = \ mathbf {X} \ mathbf {X} ^ H = \ mathbf {A} \ mathbf {R} _ {ss} \ mathbf {A} ^ H + \ mathbf {R} _ {nn}$

Condiciones

Introducimos una condición importante a considerar: el límite de resolución del ángulo de Rayleigh:

$sin (\ theta_R) = \ frac {\ lambda} {D}$

donde $D = M \ Delta$ Es la longitud de la red lineal.

Redefinimos el ángulo de llegada de una onda electromagnética a través del concepto de frecuencia espacial:

$\ mu_R = \ frac {2 \ pi} {\ lambda} \ Delta sin (\ theta_R) = \ frac {2 \ pi} {\ lambda} \ Delta \ frac {\ lambda} {\ Delta M} = \ frac { 2 \ pi} {M}$

donde $\ mu_R$ - hay un ancho estándar del lóbulo principal del haz ( ancho de haz estándar ).

Para verificar cuán efectivo es nuestro método y bajo qué condiciones, presentamos algunos valores dados para la separación angular:

$\ mu_1 = - \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = \ mu_R \ quad$ - división en un ancho de haz;
$\ mu_1 = -0.5 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0.5 \ mu_R \ quad$ - división en un segundo ancho de haz;
$\ mu_1 = -0.3 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0.3 \ mu_R \ quad$ - división en tres décimas del ancho del haz.

Defina los parámetros de entrada:

 M = 10 #    () SNR = 10 #  - (dB) d = 3 #     N = 50 #  "" (snapshots) S = ( np.sign(np.random.randn(d,N)) + 1j * np.sign(np.random.randn(d,N)) ) / np.sqrt(2) # QPSK W = ( np.random.randn(M,N) + 1j * np.random.randn(M,N) ) / np.sqrt(2) * 10**(-SNR/20) # AWGN #  : # sqrt(N0/2)*(G1 + jG2), #  G1  G2 -   . # .. Es( )  QPSK  1 ,    (noise spectral density): # N0 = (Es/N)^(-1) = SNR^(-1) [] (   ,  SNR = Es/N0); #    : # SNR_dB = 10log10(SNR) => N0_dB = -10log10(SNR) = -SNR_dB []; #    SNR    (..  ),   : # SNR = 10^(SNR_dB/10) => sqrt(N0) = (10^(-SNR_dB/10))^(1/2) = 10^(-SNR_dB/20) mu_R = 2*np.pi / M

Un poco de teoría sobre el método en sí

En primer lugar, observamos que el progenitor del método MUSIC es el método Pisarenko (1973). El problema considerado del método Pisarenko era estimar las frecuencias de la suma de exponenciales complejos en ruido blanco. V.F. Pisarenko demostró que se pueden encontrar frecuencias de vectores propios correspondientes al valor propio mínimo de la matriz de autocorrelación. Posteriormente, este método se convirtió en un caso especial del método MUSIC. [2, p. 459]

Schmidt y sus colegas propusieron el algoritmo de clasificación de señal múltiple (MUSIC) en 1979 [4]. El enfoque principal de este algoritmo es descomponer la matriz de covarianza de la señal recibida en valores propios. Dado que este algoritmo tiene en cuenta el ruido no correlacionado, la matriz de covarianza generada tiene una forma diagonal. Aquí, los subespacios de señal y ruido se calculan utilizando álgebra lineal y son ortogonales entre sí. Por lo tanto, el algoritmo utiliza la propiedad de ortogonalidad para extraer subespacios de señal y ruido [5].

El algoritmo MUSIC generalizado se puede definir de la siguiente manera:

Encuentra la matriz de covarianza $\ mathbf {R} _ {xx}$
Encuentre vectores propios a través de EVD u otro algoritmo numérico adecuado:

$\ mathbf {R} _ {xx} = \ mathbf {U} \ mathbf {\ Lambda} \ mathbf {U} ^ H \ qquad (1)$

Encuentre el pseudo espectro (por qué con el prefijo pseudo, discutiremos a continuación) MÚSICA a través de la siguiente fórmula:

$P_ {MU} (e ^ {j \ omega}) = \ frac {1} {\ sum \ limits_ {i = d + 1} ^ {M} | \ mathbf {a} ^ H \ mathbf {u} _i | ^ 2} \ qquad (2)$

donde $\ mathbf {a} = \ begin {bmatrix} e ^ {j0 \ omega} & e ^ {j1 \ omega} & e ^ {j2 \ omega} & ... & e ^ {j (M-1) \ omega } \ end {bmatrix} ^ T$ Es el vector de exponenciales para la frecuencia ω que se encuentra en un rango dado, y $\ mathbf {u} _i$ - el i-ésimo vector propio (vector propio) de la matriz de covarianza (1) correspondiente al subespacio de ruido de la matriz (1) - de ahí la indexación con $d + 1$ ( $d$ Es el rango de la matriz (1)).

Para mayor claridad, intente ejecutar el script MATLAB apropiado proporcionado por referencia . Presta atención a dos puntos principales:
en lugar de calcular el cuadrado de la segunda norma en el denominador (2), los autores aplican el algoritmo FFT a vectores propios, lo que facilita el modelado mediante el uso de funciones integradas y, en general, no contradice la teoría desde un punto de vista matemático;
la matriz de covarianza se calcula a través de matrices convolucionales; anteriormente se mostró un enfoque diferente para estimar las frecuencias espaciales.

Como se puede adivinar por el nombre, MUSIC también es un método clásico para estimar la dirección de recepción con alta resolución. El algoritmo para calcular los pseudo-espectros en este contexto se da a continuación:

encontramos la matriz de covarianza de la señal recibida;
encuentra el subespacio cero $\ mathbf {U} _0$ :

$\ mathbf {U} = [\ mathbf {U} _s \ quad \ mathbf {U} _0]$

seleccione un rango de búsqueda:

$a (\ mu) = \ begin {bmatrix} e ^ {j0 \ mu_1} & ... & e ^ {j0 \ mu_Q} \\ ... & ... & ... \\ e ^ {j ( M-1) \ mu_1} & ... & e ^ {j (M-1) \ mu_Q} \ end {bmatrix}$

donde $\ mu = - \ frac {2 \ pi f_c} {c} \ Delta sin \ theta = - \ frac {2 \ pi} {\ lambda} \ Delta sin \ theta$

calcular el pseudo espectro:

$P_ {MU} (\ theta) = \ frac {\ mathbf {a} ^ H (\ theta) \ mathbf {a} (\ theta)} {\ mathbf {a} ^ H (\ theta) \ mathbf {U} _0 \ mathbf {U} _0 ^ H \ mathbf {a} (\ theta)}$

La relación entre el análisis espectral y el análisis de ángulos de llegada (DoA - dirección de arriaval) de las ondas EM se describe en la tabla 1.

Tabla 1 Comunicación entre aplicaciones MUSIC : procesamiento de matriz de señal y búsqueda armónica [6].

Variable	Procesamiento de matriz de señal	Búsqueda armónica
$M$	Numero de sensores	El número de períodos de tiempo.
$N$	El número de períodos de tiempo.	Numero de experimentos
$d$	Número de frentes de ola	El número de componentes complejos.
$\ mu$	Frecuencias espaciales	Frecuencias normalizadas

En general, el proceso de recibir a través de matrices (rejillas) se puede comparar con el proceso de discretización clásica, porque de hecho, cada sensor, que recibe una onda con un cierto retraso de fase (es decir, con un cierto retraso de tiempo), realiza las funciones de un pulso delta de muestreo. El número de realizaciones (experimentos) del análisis espectral clásico corresponderá al número de segmentos de tiempo (instantáneas). Cada fuente tendrá su propio frente de onda, que es equivalente al número de sinusoides únicos de la señal en el caso del análisis espectral.

Y ahora volviendo al momento de calcular los vectores propios. Ya mencionamos anteriormente que los vectores $a (\ theta_i) \ epsilon A$ donde $i = 1,2, .., d$ son ortogonales al subespacio de ruido de la matriz de covarianza, es decir:

$a (\ theta_i) ^ TU_0 = 0 ^ T$

En realidad, vemos un sistema de ecuaciones, resolviendo en qué podemos encontrar las raíces: vectores propios. Tal método, en contraste con los algoritmos numéricos (que, como señalamos anteriormente, se aplica a EVD), permite obtener valores propios reales en lugar de aproximados. Es por eso que este enfoque nos permite obtener no un pseudoespectro, sino un espectro. La misma idea formó la base del algoritmo Root MUSIC .

Modelado

Fuf! Finalmente, todas las fórmulas se describen y explican de alguna manera. Podemos comenzar a modelar.

 cases = [[-1., 0, 1.], [-0.5, 0, 0.5], [-0.3, 0, 0.3],] for idxm, c in enumerate(cases): #   ( ): mu_1 = c[0]*mu_R mu_2 = c[1]*mu_R mu_3 = c[2]*mu_R #   a_1 = np.exp(1j*mu_1*np.arange(M)) a_2 = np.exp(1j*mu_2*np.arange(M)) a_3 = np.exp(1j*mu_3*np.arange(M)) A = (np.array([a_1, a_2, a_3])).T #    X = np.dot(A,S) + W #    R = np.dot(X,np.matrix(X).H) U, Sigma, Vh = np.linalg.svd(X, full_matrices=True) U_0 = U[:,d:] #   thetas = np.arange(-90,91)*(np.pi/180) #   mus = np.pi*np.sin(thetas) #    a = np.empty((M, len(thetas)), dtype = complex) for idx, mu in enumerate(mus): a[:,idx] = np.exp(1j*mu*np.arange(M)) # MVDR: S_MVDR = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MVDR[idx] = 1 / (np.dot(np.matrix(a_idx).H, np.dot(np.linalg.pinv(R),a_idx))) # MUSIC: S_MUSIC = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MUSIC[idx] = np.dot(np.matrix(a_idx).H,a_idx)\ / (np.dot(np.matrix(a_idx).H, np.dot(U_0,np.dot(np.matrix(U_0).H,a_idx)))) plt.subplots(figsize=(10, 5), dpi=150) plt.semilogy(thetas*(180/np.pi), np.real( (S_MVDR / max(S_MVDR))), color='green', label='MVDR') plt.semilogy(thetas*(180/np.pi), np.real((S_MUSIC/ max(S_MUSIC))), color='red', label='MUSIC') plt.grid(color='r', linestyle='-', linewidth=0.2) plt.xlabel('Azimuth angles θ (degrees)') plt.ylabel('Power (pseudo)spectrum (normalized)') plt.legend() plt.title('Case #'+str(idxm+1)) plt.show()

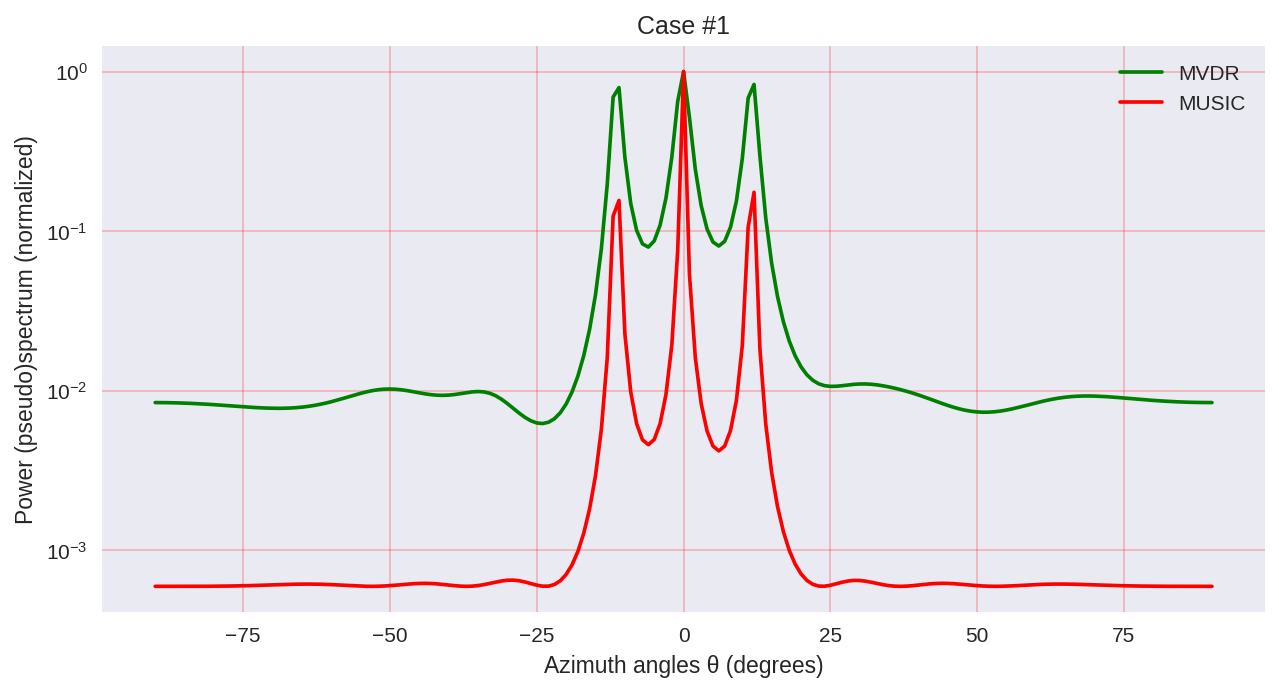
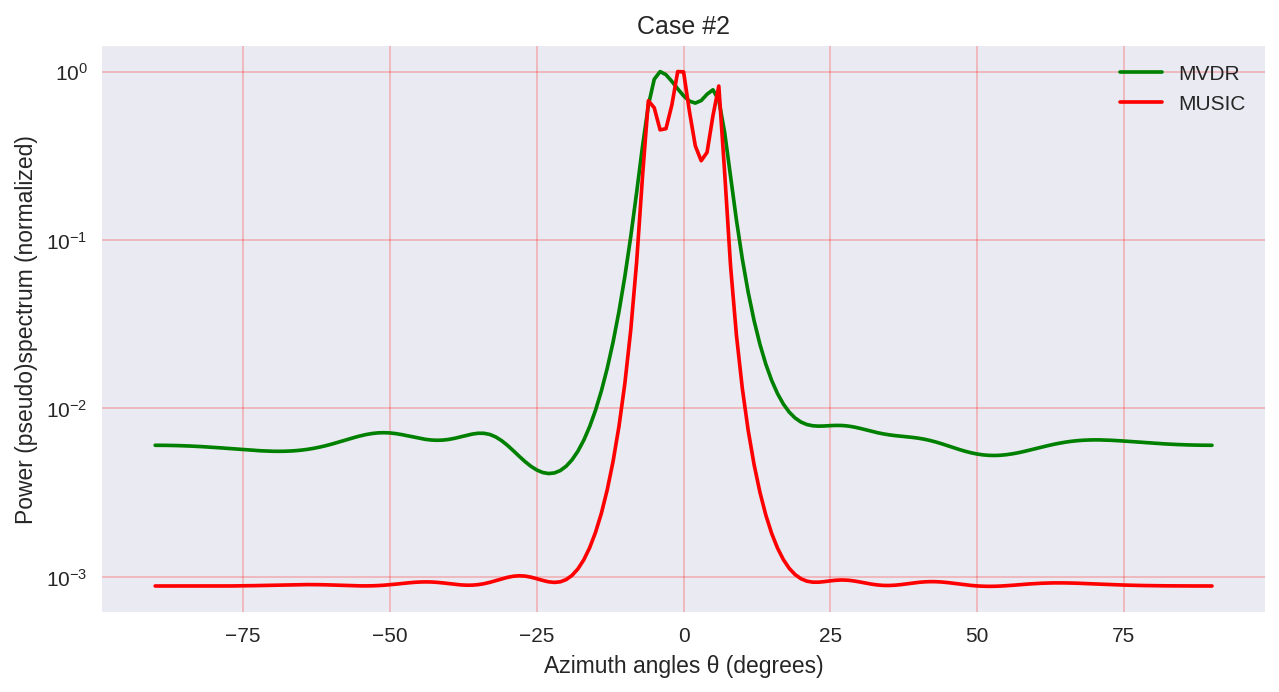
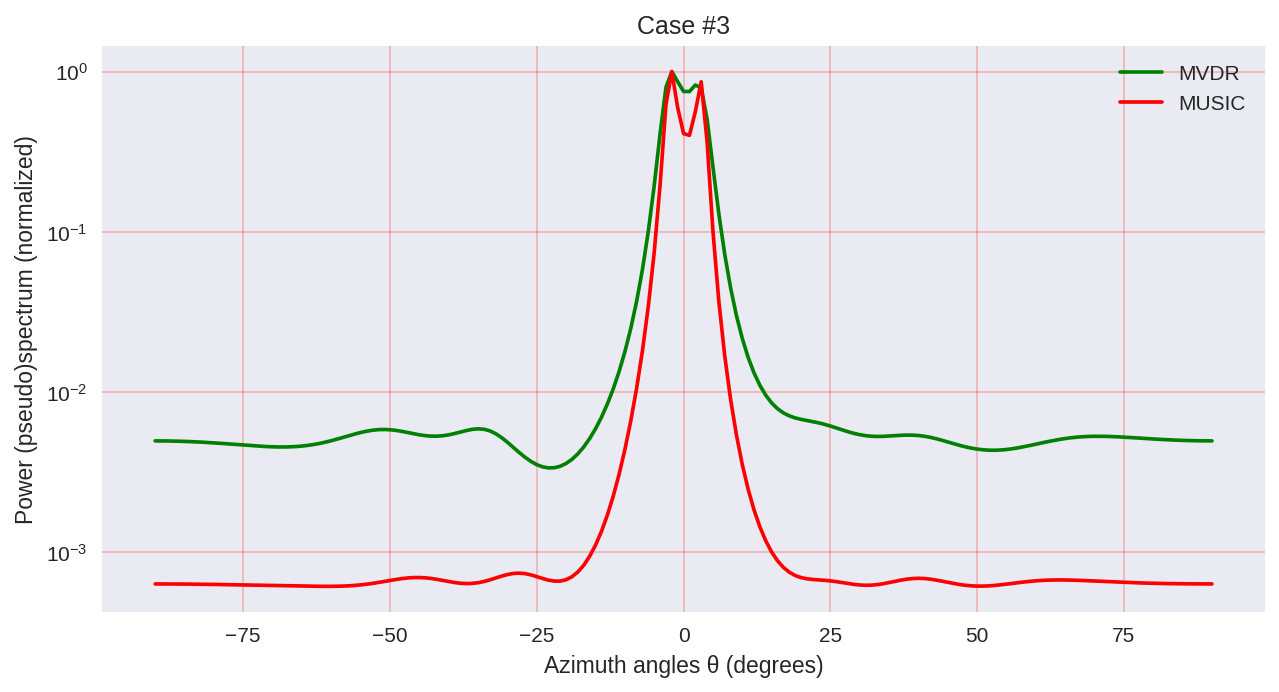
Como podemos ver, MUSIC tiene una resolución más alta y permite lograr, en general, mejores resultados que, por ejemplo, MVDR permite, el mismo representante de los métodos paramétricos de análisis espectral.

Sin embargo, debe tenerse en cuenta que cuando usamos MUSIC usamos algoritmos más computacionalmente caros, como EVD o SVD, que tiene un precio para una mayor precisión.

Tales cosas

Lista de literatura utilizada:

Haykin, Simon y KJ Ray Liu. Manual sobre procesamiento de matriz y redes de sensores. Vol. 63. John Wiley & Sons, 2010. pp. 102-107
Hayes MH Procesamiento y modelado estadístico de señales digitales. - John Wiley & Sons, 2009.
Haykin, Simon S. Teoría del filtro adaptativo. Pearson Education India, 2008. pp. 422-427
Richmond, Christ D. "Umbral de error medio-cuadrado del algoritmo de capón predicción SNR y probabilidad de resolución". Transacciones IEEE sobre procesamiento de señales 53.8 (2005): 2748-2764.
SKP Gupta, MUSIC y algoritmo MUSIC mejorado para estimar la dorección de llegada, IEEE, 2015.
Conferencias del profesor Martin Haardt ( array array )

Modelamos el algoritmo MUSIC para determinar la dirección de llegada de una onda electromagnética