Aprendizaje profundo en computación de flujo óptico

Con el advenimiento de muchas arquitecturas de redes neuronales diferentes, muchas técnicas clásicas de visión por computadora son cosa del pasado. Cada vez menos personas usan SIFT y HOG para la detección de objetos, y MBH para el reconocimiento de acciones, y si lo usan, es más como signos hechos a mano para las cuadrículas correspondientes. Hoy vamos a ver uno de los problemas clásicos de CV en el que los métodos clásicos aún mantienen el liderazgo, mientras que las arquitecturas DL los respiran lánguidamente en la parte posterior de la cabeza.

Estimación de flujo óptico.

La tarea de calcular el flujo óptico entre dos imágenes (generalmente entre cuadros adyacentes de un video) es construir un campo vectorial $$$O$del mismo tamaño, por otra parte $$$O (i, j)$corresponderá al vector aparente de desplazamiento de píxeles $$$(i, j)$del primer cuadro al segundo. Al construir dicho campo vectorial entre todos los cuadros adyacentes del video, obtenemos una imagen completa de cómo se mueven ciertos objetos sobre él. En otras palabras, esta es la tarea de rastrear todos los píxeles en un video. El flujo óptico se usa de manera extremadamente amplia: en las tareas de reconocimiento de acciones, por ejemplo, un campo vectorial de este tipo le permite concentrarse en los movimientos que ocurren en el video y alejarse de su contexto [7]. Incluso las aplicaciones más comunes son la odometría visual, la compresión de video, el procesamiento posterior (por ejemplo, agregar un efecto de cámara lenta) y mucho más.



Hay espacio para algunas ambigüedades: ¿qué se considera exactamente un sesgo visible desde el punto de vista de las matemáticas? Por lo general, se supone que los valores de píxeles van de un cuadro a otro sin cambios, en otras palabras:

$$

$$I (i, j, t) = I (i + u_i, j + u_j, t + 1),$$

donde $$$I (i, j, t)$- intensidad de píxeles en coordenadas $$$(i, j)$entonces flujo óptico $$$(u_i, u_j)$muestra dónde se ha movido este píxel al siguiente punto en el tiempo (es decir, en el siguiente cuadro).

En la imagen se ve así:





Visualizar un campo vectorial directamente con vectores es visual, pero no siempre es conveniente, por lo tanto, la segunda forma común es visualizar con color:





Cada color en esta imagen codifica un vector específico. Para simplificar, se recortan vectores de más de 20, y el vector en sí mismo se puede restaurar por color a partir de la siguiente imagen:




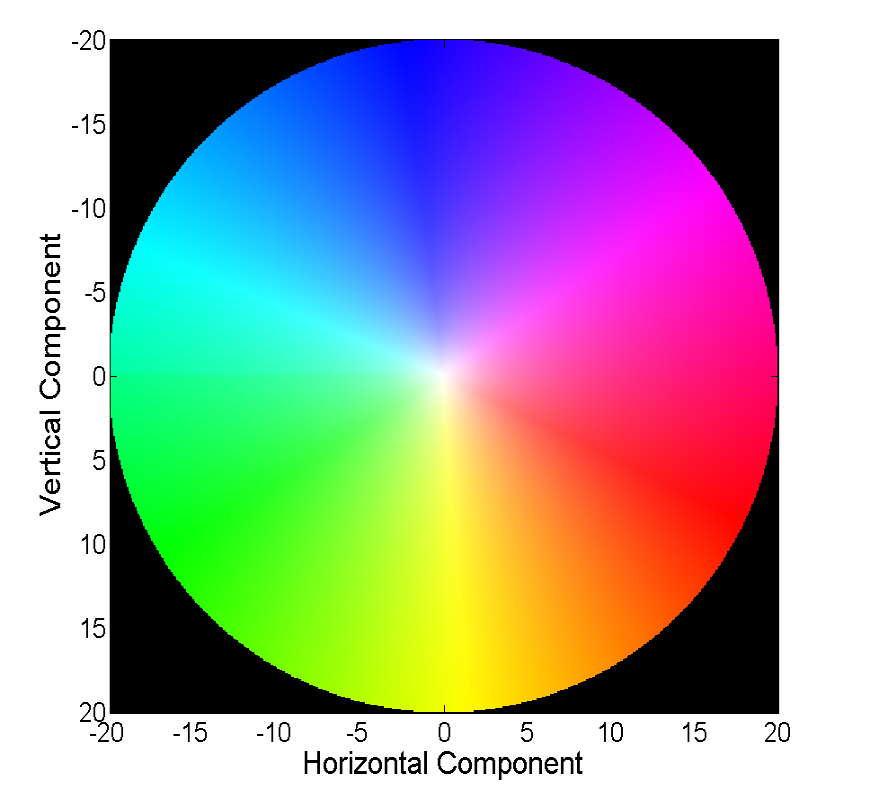
Los métodos clásicos han logrado una precisión bastante buena, que a veces tiene un precio. Consideraremos el progreso que las redes neuronales han logrado en la solución de este problema en los últimos 4 años.

Datos y métricas

Dos palabras sobre qué conjuntos de datos estaban disponibles y populares al comienzo de nuestra historia (es decir, 2015), y cómo medir la calidad del algoritmo resultante.

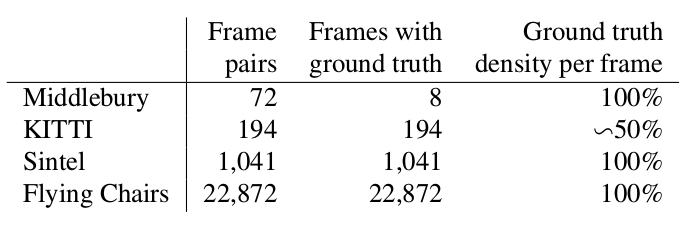
Middlebury

Un pequeño conjunto de datos de 8 pares de imágenes con pequeños desplazamientos, que, sin embargo, a veces se usa para validar algoritmos para calcular el flujo óptico incluso ahora.

Gatito

Este es un conjunto de datos marcado para aplicaciones para automóviles sin conductor y ensamblado con tecnología LIDAR. Es ampliamente utilizado para validar algoritmos de cálculo de flujo óptico y contiene muchos casos bastante complicados con transiciones bruscas entre cuadros.

Sintel

Otro punto de referencia muy común creado sobre la base del dibujo abierto y dibujado de Sintel en Blender en dos versiones, que se designan como limpio y final. El segundo es mucho más complicado, porque contiene muchos efectos atmosféricos, ruido, desenfoque y otros problemas para los algoritmos para calcular el flujo óptico.

EPE

La función de error estándar para la tarea de cálculo del flujo óptico es Error de punto final o EPE. Esto es simplemente la distancia euclidiana entre el algoritmo calculado y el flujo óptico verdadero, promediado sobre todos los píxeles.

Flownet (2015)

Al embarcarse en la construcción de una arquitectura de red neuronal para la tarea de calcular el flujo óptico en 2015, los autores (de las universidades de Múnich y Friburgo) enfrentaron dos problemas: no había un gran conjunto de datos marcado para esta tarea, y marcarlo manualmente sería difícil (intente marcar dónde me he movido cada píxel de la imagen en el siguiente cuadro), en primer lugar. Esta tarea era bastante diferente de todas las tareas que se resolvieron con la ayuda de arquitecturas CNN antes de eso, en segundo lugar. De hecho, esta es una tarea de regresión píxel por píxel, lo que la hace similar a la tarea de segmentación (clasificación píxel por píxel), pero en lugar de una imagen, tenemos dos entradas, e intuitivamente, los signos deben mostrar de alguna manera la diferencia entre las dos imágenes. Como primera iteración, se decidió simplemente hacer estallar dos cuadros RGB como entrada (habiendo recibido, de hecho, una imagen de 6 canales), entre los cuales queremos calcular el flujo óptico, y tomar U-net como una arquitectura con una serie de cambios. Esta red se llamaba FlowNetS (S significa Simple):





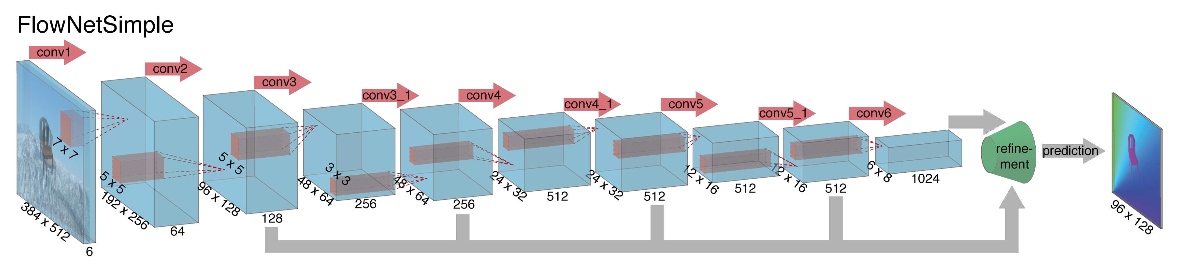
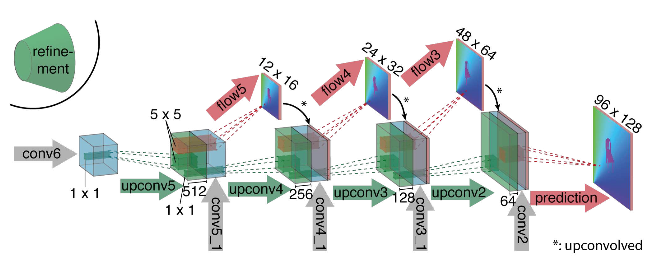
Como puede ver en el diagrama, el codificador no se nota, el decodificador difiere de las opciones clásicas de varias maneras:

1. La predicción del flujo óptico ocurre no solo desde el último nivel, sino también desde todos los demás. Para obtener Ground Truth para el i-ésimo nivel del decodificador, el objetivo original (es decir, el flujo óptico) simplemente se reduce (casi lo mismo que la imagen) a la resolución deseada, y el predicado obtenido en el i-ésimo nivel va más allá, t es decir, se concatena con un mapa de características que emerge de este nivel. La función general de las pérdidas de entrenamiento será una suma ponderada de pérdidas de todos los niveles del decodificador, mientras que el peso en sí será mayor, cuanto más cerca esté el nivel de la salida de la red. Los autores no dan una explicación de por qué se hace esto, pero lo más probable es que la razón sea el hecho de que los movimientos bruscos son mejores para detectar en los primeros niveles, entonces los vectores en el flujo óptico de baja resolución no serán tan grandes.
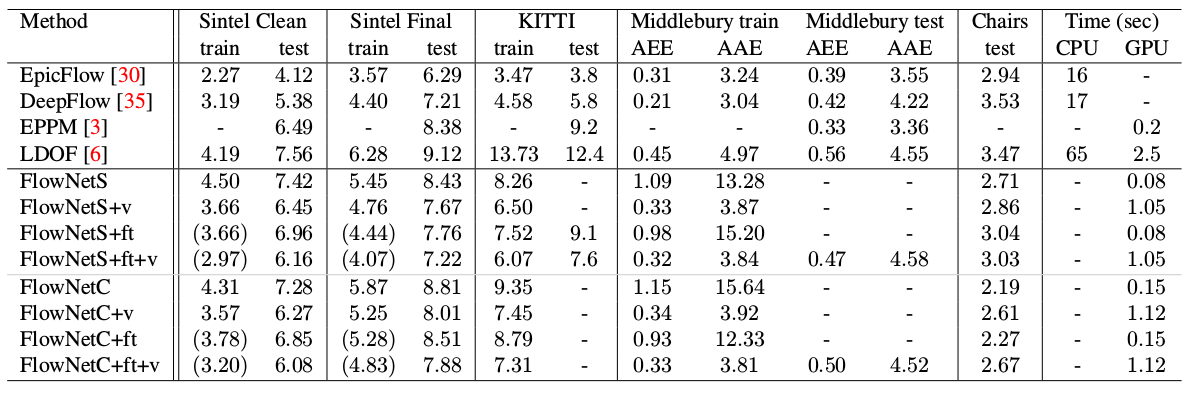
2. El diagrama muestra que la resolución de entrada de las imágenes es 384x512, y la salida es cuatro veces menor. Los autores notaron que si aumenta esta salida a 384x512 por interpolación bilineal simple, dará la misma calidad que si conecta dos niveles más del decodificador. También puede usar el enfoque variacional [2], que demuestra la calidad (+ v en la tabla con calidad).
3. Como en U-net, las tarjetas de atributos del codificador se envían al decodificador y se concatenan como se muestra en el diagrama.

Para comprender cómo los autores trataron de mejorar su línea de base, necesita saber cuál es la correlación entre las imágenes y por qué puede ser útil para calcular el flujo óptico. Entonces, teniendo dos imágenes y sabiendo que el segundo es el siguiente cuadro en el video en relación con el primero, podemos intentar comparar el área alrededor del punto en el primer cuadro (para el que queremos encontrar un cambio al segundo cuadro) con áreas del mismo tamaño en la segunda imagen. Además, suponiendo que el cambio no pueda ser demasiado grande por unidad de tiempo, la comparación solo puede considerarse en un determinado vecindario del punto de partida. Para esto, se utiliza la correlación cruzada. Vamos a ilustrar con un ejemplo.

Tome dos cuadros adyacentes del video, queremos determinar dónde un cierto punto ha cambiado del primer cuadro al segundo. Suponga que alguna área alrededor de este punto ha cambiado de la misma manera. De hecho, los píxeles vecinos en un video generalmente se compensan, como lo más probable, visualmente, son parte de un objeto. Este supuesto se usa activamente, por ejemplo, en enfoques diferenciales, que se pueden leer con más detalle en [5], [6].

fig, ax = plt.subplots(1, 2, figsize=(20, 10)) ax[0].imshow(frame1) ax[1].imshow(frame2); 

Tratemos de tomar un punto en el centro de la pata del gatito y encontrarlo en el segundo cuadro. Toma un área alrededor.

 patch1 = frame1[90:190, 140:250] plt.imshow(patch1); 

Calculamos la correlación entre esta área (en la literatura inglesa a menudo escribimos plantillas o parches a partir de la primera imagen) y la segunda imagen. La plantilla simplemente "caminará" a través de la segunda imagen y calculará el siguiente valor entre sí misma y piezas del mismo tamaño en la segunda imagen:



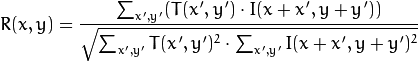
Cuanto mayor sea el valor de este valor, más se verá la plantilla como la pieza correspondiente en la segunda imagen. Con OpenCV, esto se puede hacer así:

 corr = cv2.matchTemplate(frame2, patch1, cv2.TM_CCORR_NORMED) plt.imshow(corr, cmap='gray'); 

Se pueden encontrar más detalles en [7].

El resultado es el siguiente:



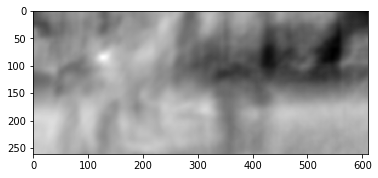
Vemos un pico claro, indicado en blanco. Encuéntralo en el segundo cuadro:

 min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(corr) h, w, _ = patch1.shape top_left = max_loc bottom_right = (top_left[0] + w, top_left[1] + h) frame2_copy = frame2.copy() cv2.rectangle(frame2_copy, top_left, bottom_right, 255, 2) plt.imshow(frame2_copy); 

Vemos que el pie se encontró correctamente, de acuerdo con estos datos, podemos entender en qué dirección se movió del primer cuadro al segundo y calcular el flujo óptico correspondiente. Además, resulta que esta operación es bastante resistente a las distorsiones fotométricas, es decir. Si el brillo en el segundo cuadro aumenta bruscamente, el pico de correlación cruzada entre las imágenes permanecerá en su lugar.

Teniendo en cuenta todo lo anterior, los autores decidieron introducir la llamada capa de correlación en su arquitectura, pero se decidió no considerar la correlación según las imágenes de entrada, sino según los mapas de características después de varias capas de codificador. Tal capa, por razones obvias, no tiene parámetros de aprendizaje, aunque en esencia es similar a la convolución, pero en lugar de filtros, aquí no usamos pesos, sino alguna área de la segunda imagen:



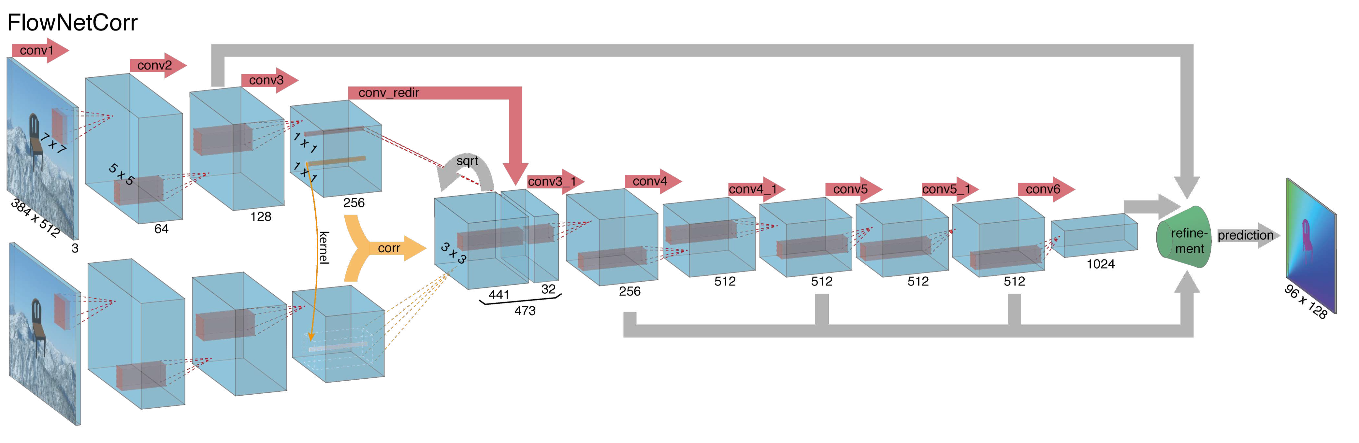
Por extraño que parezca, este truco no proporcionó una mejora significativa en la calidad de los autores de este artículo, sin embargo, se aplicó con más éxito en trabajos posteriores, y en [9] los autores pudieron demostrar que al cambiar ligeramente los parámetros de entrenamiento, FlowNetC puede funcionar mucho mejor.

Los autores resolvieron el problema con la falta de un conjunto de datos de una manera bastante elegante: rasparon 964 imágenes de Flickr sobre los temas: "ciudad", "paisaje", "montaña" en la resolución de 1024 × 768 y utilizaron su recorte 512 × 384 como fondo, que luego arrojó algunas sillas de un conjunto abierto de modelos 3D prestados. Luego, varias transformaciones afines se aplicaron independientemente a las sillas y al fondo, que se utilizaron para generar la segunda imagen en un par y el flujo óptico entre ellas. El resultado es el siguiente:





Un resultado interesante fue que el uso de un conjunto de datos sintético de este tipo hizo posible lograr una calidad relativamente buena para los datos de otro dominio. El ajuste fino en los datos correspondientes, por supuesto, demostró más cualidades (+ pies en la tabla a continuación):



El resultado en videos reales se puede ver aquí:

SpyNet (2016)

En muchos artículos posteriores, los autores trataron de mejorar la calidad resolviendo el problema del mal reconocimiento de los movimientos repentinos. Intuitivamente, el movimiento no será capturado por la red si su vector va significativamente más allá del campo receptivo de activación. Se propone resolver este problema debido a tres cosas: una convolución mayor, pirámides y "deformar" una imagen de un par en una corriente óptica. Todo en orden.

Entonces, si tenemos un par de imágenes en las que el objeto se ha desplazado bruscamente (más de 10 píxeles), entonces simplemente podemos reducir la imagen (en 6 o más veces). El valor absoluto del desplazamiento disminuirá significativamente, y es más probable que la red pueda "atraparlo", especialmente si sus convoluciones son mayores que el desplazamiento en sí (en este caso, se usan convoluciones 7x7).



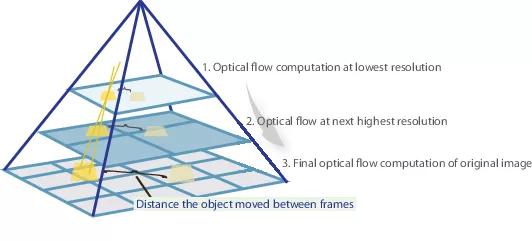
Sin embargo, al reducir la imagen, perdimos muchos detalles importantes, por lo que debemos pasar al siguiente nivel de la pirámide, en el que el tamaño de la imagen ya es más grande, teniendo en cuenta de alguna manera la información que recibimos antes cuando calculamos el flujo óptico en un tamaño más pequeño. Esto se realiza utilizando el operador de deformación, que relata la primera imagen de acuerdo con la aproximación disponible del flujo óptico (obtenido en el nivel anterior). Una mejora en este caso es que la primera imagen que se "empuja" de acuerdo con la aproximación del flujo óptico estará más cerca de la segunda que la original, es decir, nuevamente reduciremos el valor absoluto del flujo óptico, que debemos predecir (recordar, pequeño en valor los movimientos se detectan mucho mejor, ya que están completamente incluidos en una convolución). Desde el punto de vista de las matemáticas, con una imagen de mapa de bits I y una aproximación del flujo óptico V, el operador de deformación se puede describir de la siguiente manera:

$$

$$w (I, V) = I_w, \; \; I_w (x) = I (x + V (x)),$$

donde $$$x = (i, j)$es decir un punto específico en la imagen $$$I$- la imagen en sí $$$V$- flujo óptico $$$I_w$- la imagen resultante, "envuelta" en la corriente óptica.

¿Cómo aplicar todo esto en la arquitectura CNN? Arreglamos la cantidad de niveles piramidales $$$k$y un factor por el cual cada imagen subsiguiente se reduce a un nivel que comienza desde el último $$$n$. Denote por $$$d (*)$y $$$u (*)$las funciones de disminución y muestreo de la imagen o flujo óptico por este factor.

También obtendremos un conjunto de CNN-ok { $$$G_0 ... G_k$}, uno para cada nivel de la pirámide. Entonces $$$G_i$-th network aceptará un par de imágenes con $$$i$nivel de pirámide y flujo óptico calculado en $$$G_ {i-1}$nivel ( $$$G_0$solo aceptará un tensor de ceros en su lugar). En este caso, enviaremos una de las imágenes a la capa de deformación para reducir la diferencia entre ellas, y no predeciremos el flujo óptico a este nivel, sino el valor que debe agregarse al flujo óptico incrementado (muestreado) del nivel anterior para obtener el flujo óptico a este nivel En la fórmula, se ve así:

$$

$$v_k = G_k (I_k ^ 1, w (I_k ^ 2, u (V_ {k-1})), V_ {k-1})$$

Para obtener el flujo óptico en sí, simplemente agregamos el predicado de red y el flujo aumentado desde el nivel anterior:

$$

$$V_k = u (V_ {k-1}) + v_k.$$

Para obtener Ground Truth para la red en este nivel, necesitamos hacer la operación opuesta: restar el predicado del objetivo (reducido al nivel deseado) del nivel anterior de la pirámide. Esquemáticamente, se ve así:



La ventaja de este enfoque es que podemos enseñar cada nivel de forma independiente. Los autores comenzaron a entrenar desde el nivel 0, cada red posterior se inicializó con los parámetros de la anterior. Desde cada red $$$G_i$resuelve el problema mucho más simple que el cálculo completo del flujo óptico en una imagen grande, entonces los parámetros se pueden hacer mucho menos. Tanto es así que ahora todo el conjunto puede caber en dispositivos móviles:



El conjunto en sí es el siguiente (un ejemplo de una pirámide de 3 niveles):



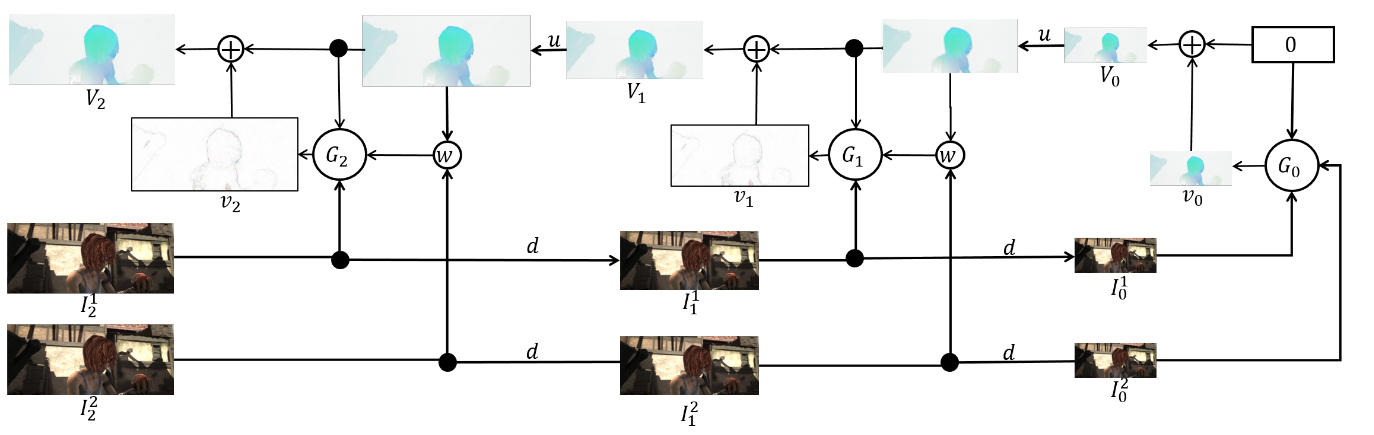
Queda por hablar directamente sobre arquitectura. $$$G_i$red y hacer balance. Cada red $$$G_i$consta de 5 capas convolucionales, cada una de las cuales termina con la activación de ReLU, excepto la última (que predice el flujo óptico). El número de filtros en cada capa es respectivamente { $$$32, 64, 32, 16, 2$}. Las entradas de la red neuronal (la imagen, la segunda imagen "envuelta" en el flujo óptico y el flujo óptico en sí) simplemente se concatenan de acuerdo con la dimensión de los canales, por lo que su tensor de entrada tiene 8. Los resultados son impresionantes:

PWC-Net (2018)

Inspirados por el éxito de sus colegas alemanes, los muchachos de NVIDIA decidieron aplicar su experiencia (y tarjetas de video) para mejorar aún más el resultado. Su trabajo se basó en gran medida en ideas del modelo anterior (SpyNet), por lo que PWC-Net también tratará con pirámides, pero con pirámides de convolución, no las imágenes originales, sin embargo, en orden.

El uso de intensidades de píxeles sin procesar para calcular el flujo óptico no siempre es razonable, porque Un cambio brusco en el brillo / contraste romperá nuestra suposición de que los píxeles se mueven de un cuadro a otro sin cambios y el algoritmo no será resistente a dichos cambios. En los algoritmos clásicos para calcular el flujo óptico, se utilizan varias transformaciones que mitigan esta situación, en este caso, los autores decidieron proporcionar al modelo la oportunidad de aprender ellos mismos. Por lo tanto, en lugar de la pirámide de imagen en PWC-Net, se utilizan pirámides de convolución (de ahí la primera letra en Pwc-Net), es decir. solo mapas de características de diferentes capas de CNN, que aquí se llama extractor de pirámide de características.

Entonces, todo es casi como en SpyNet, justo antes de enviarlo a CNN, que se llama estimador de flujo óptico, todo lo que necesita, a saber:

• imagen (en este caso, un mapa de características del extractor de pirámides de características),
• el flujo óptico muestreado arriba calculado en el nivel anterior,
• la segunda imagen, "envuelta" (recuerde la capa de deformación, de ahí la segunda letra en pWc-Net) en esta corriente óptica,

entre el segundo cuadro "envuelto" y el primero habitual (de nuevo, le recuerdo que en lugar de imágenes sin procesar, aquí se usan tarjetas de características con extractor de pirámides de características) considere lo que se llama volumen de costos (de ahí la tercera letra en pwC-Net) y que esencialmente ya está correlación previamente considerada entre dos imágenes.



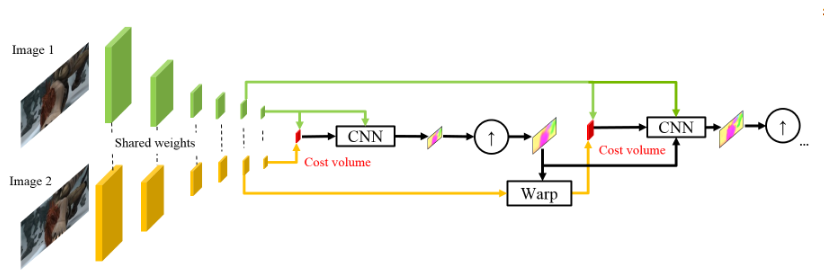
El toque final es la red de contexto, que se agrega inmediatamente después del estimador de flujo óptico y desempeña el papel de procesamiento posterior capacitado para el flujo óptico calculado. Los detalles arquitectónicos se pueden ver debajo del spoiler o en el artículo original.


Los resultados son aún más impresionantes:



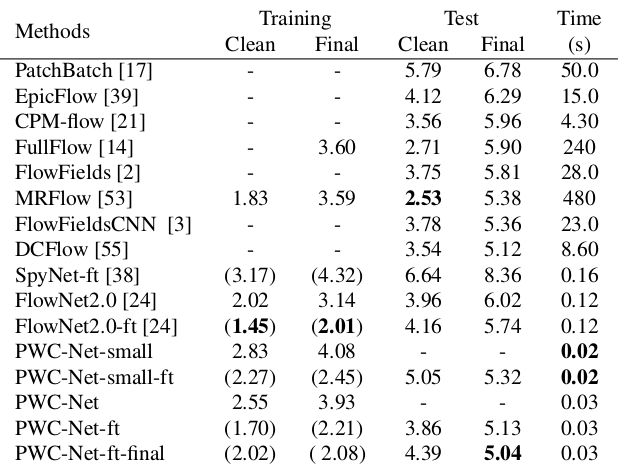
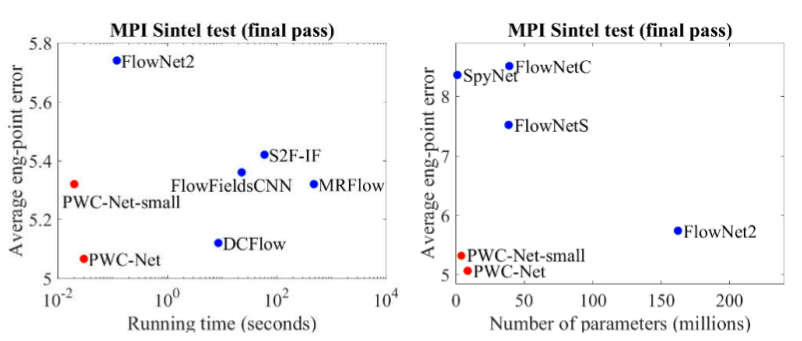
En comparación con otros métodos de CNN para calcular el flujo óptico, PWC-Net logra un equilibrio entre la calidad y la cantidad de parámetros:



También hay una excelente presentación de los propios autores, en la que hablan sobre el modelo en sí y sus experimentos:

Conclusión

La evolución de las arquitecturas que resuelven el problema del conteo de flujo óptico es un maravilloso ejemplo de cómo el progreso en las arquitecturas CNN y su combinación con métodos clásicos da el mejor y el mejor resultado. Y aunque los métodos clásicos de CV aún ganan en calidad, los resultados recientes dan la esperanza de que esto sea reparable ...

Fuentes y enlaces

1. FlowNet: Flujo óptico de aprendizaje con redes convolucionales: artículo , código .
2. Flujo óptico de gran desplazamiento: coincidencia del descriptor en la estimación del movimiento variacional: artículo .
3. Estimación del flujo óptico utilizando una red de pirámide espacial: artículo , código .
4. PWC-Net: CNNs para flujo óptico usando pirámide, deformación y volumen de costos: artículo , código .
5. Lo que quería saber sobre el flujo óptico, pero se avergonzó de preguntar: artículo .
6. Cálculo del flujo óptico por el método Lucas-Canadá. Teoría: artículo .
7. Plantilla que coincide con OpenCVP: dock .
8. Quo Vadis, ¿reconocimiento de acción? Un nuevo modelo y el conjunto de datos cinéticos: artículo .
9. FlowNet 2.0: Evolución de la estimación del flujo óptico con redes profundas: artículo , código .