🍣 🙆🏽 👨🏼‍🏭 Casi el canal MIMO más fácil con desvanecimiento (modelo Kronecker incluido) 🧖🏽 🔬 🍬

Buen dia a todos!

Considerando el tema de la diversidad espacial , ya hemos tocado los problemas de desvanecimiento en los canales de comunicación y por qué ocurre ese desvanecimiento. Hoy me propongo hablar sobre este tema con un poco más de detalle.

Además, en el artículo de hoy tocaremos ligeramente los problemas de correlación espacial de los canales MIMO, que tradicionalmente se discuten en el curso del curso de Comunicaciones Móviles ( CSP ) del Profesor Haardt y, por lo tanto, en mi opinión, dicha publicación no será superflua. Y, noto de inmediato, la gama de problemas no se limita al uso solo en comunicaciones móviles.

En general, invito a todos los interesados en el tema de las comunicaciones inalámbricas a leer, ¡y vamos!

Colin Slater "Desvaneciendo recuerdos" . Sí, reducir todo a un tema probablemente sea excesivo, pero con alguna metáfora así, creo que puedes imaginar lo que recibe el receptor después de todo tipo de influencias en la señal de información original ...

De que estamos hablando

Comencemos con el hecho de que en la naturaleza existen los llamados ruidos multiplicativos que afectan la potencia de la señal recibida: desvanecimiento .

Los términos, como habrás adivinado, no están traducidos directamente al ruso y al inglés, pero esto no es muy importante.

En la literatura inglesa, el término desvanecimiento implica una cierta influencia que, por así decirlo, hace que nuestra señal se desvanezca, "desvanezca".

En nuestra literatura, el término desvanecimiento generalmente se usa, y esto se debe principalmente al efecto de trayectoria múltiple: si una onda electromagnética encuentra su copia generada por reflejos y difracción, y están en antifase, las ondas se cancelarán entre sí, es decir, el canal , por así decirlo , se congela .

El desvanecimiento es rápido y lento (desvanecimiento rápido y lento ).

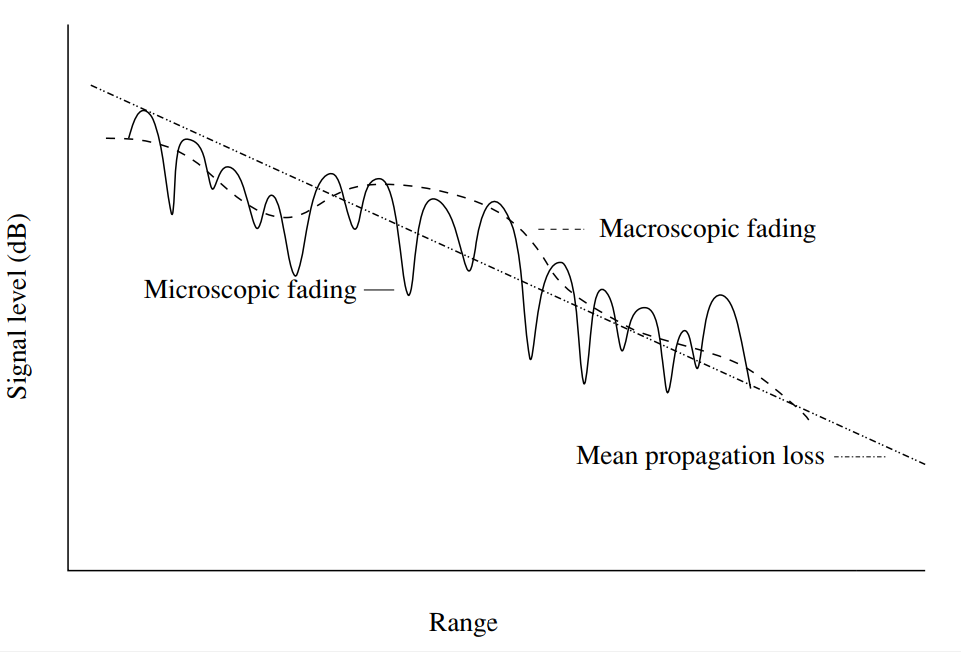
Fig. 1. Fluctuaciones en la potencia de la señal en canales inalámbricos según la distancia. El nivel promedio de pérdida de propagación aumenta de manera monótona al aumentar el rango. Pueden ocurrir desviaciones locales debido al desvanecimiento macroscópico (lento) y microscópico (rápido) [1, p.14].

Lo confieso de inmediato, hoy no trabajaremos con desvanecimiento lento, pero hablaremos de los rápidos con suficiente detalle.

Fig. 2. Ilustración del efecto de sombreado: como regla, el desvanecimiento lento ocurre debido al sombreado (sombreado). Para la simulación, generalmente se elige la distribución lognormal .

Si desea leer un poco sobre el desvanecimiento lento, en particular, y sobre cómo puede simular canales satelitales, en general, ¡lo invito aquí !

Desvanecimiento rápido

El desvanecimiento rápido ocurre, por regla general, por dos razones principales:

debido a la propagación por trayectos múltiples que ya hemos mencionado y / o
debido a los cambios de frecuencia Doppler .

Estos últimos son muy notables para los sistemas de satélite , pero no siempre se tienen en cuenta para los casos de comunicaciones terrestres debido al hecho de que las estaciones base en este caso, por regla general, son estacionarias.

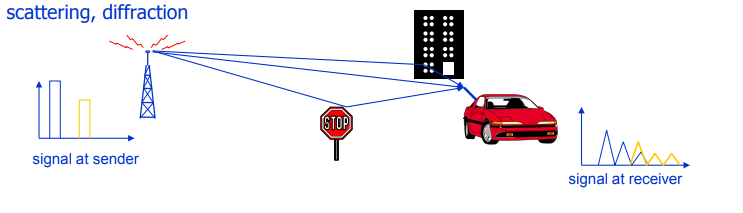
Fig. 3. Ilustración de las causas del desvanecimiento. Se presta especial atención a la dispersión y la difracción: es precisamente debido a estos fenómenos que se forma la llamada propagación multitrayecto, que conduce a la interferencia entre símbolos ( ISI ).

Pero eso está lejos de todo.

Desvanecimiento selectivo vs. Desvanecimiento plano

Arriba, dividimos nuestra interferencia por la naturaleza de la ocurrencia . Sin embargo, la interferencia también se puede dividir por la naturaleza del efecto sobre la señal transmitida . Y aquí necesitamos el concepto de selectividad de canal.

Damos una pequeña clasificación de acuerdo con [1, p. 14-18]. Entonces, el desvanecimiento rápido puede ser:

Selectivo
a. Frecuencia selectiva
b. Tiempo selectivo
c. Espacialmente selectivo (esto se relaciona con el problema de los ángulos de llegada y salida de las ondas EM; hoy no analizaremos este problema)
Plano: gravita más hacia la naturaleza del desvanecimiento lento (sí, esto es una paradoja)

Lo que implica el último término se explica de lo contrario.

Primero, si el ancho del espectro de la señal transmitida por nosotros excede el ancho de banda coherente del canal , entonces dicen que estamos tratando con interferencia selectiva de frecuencia.

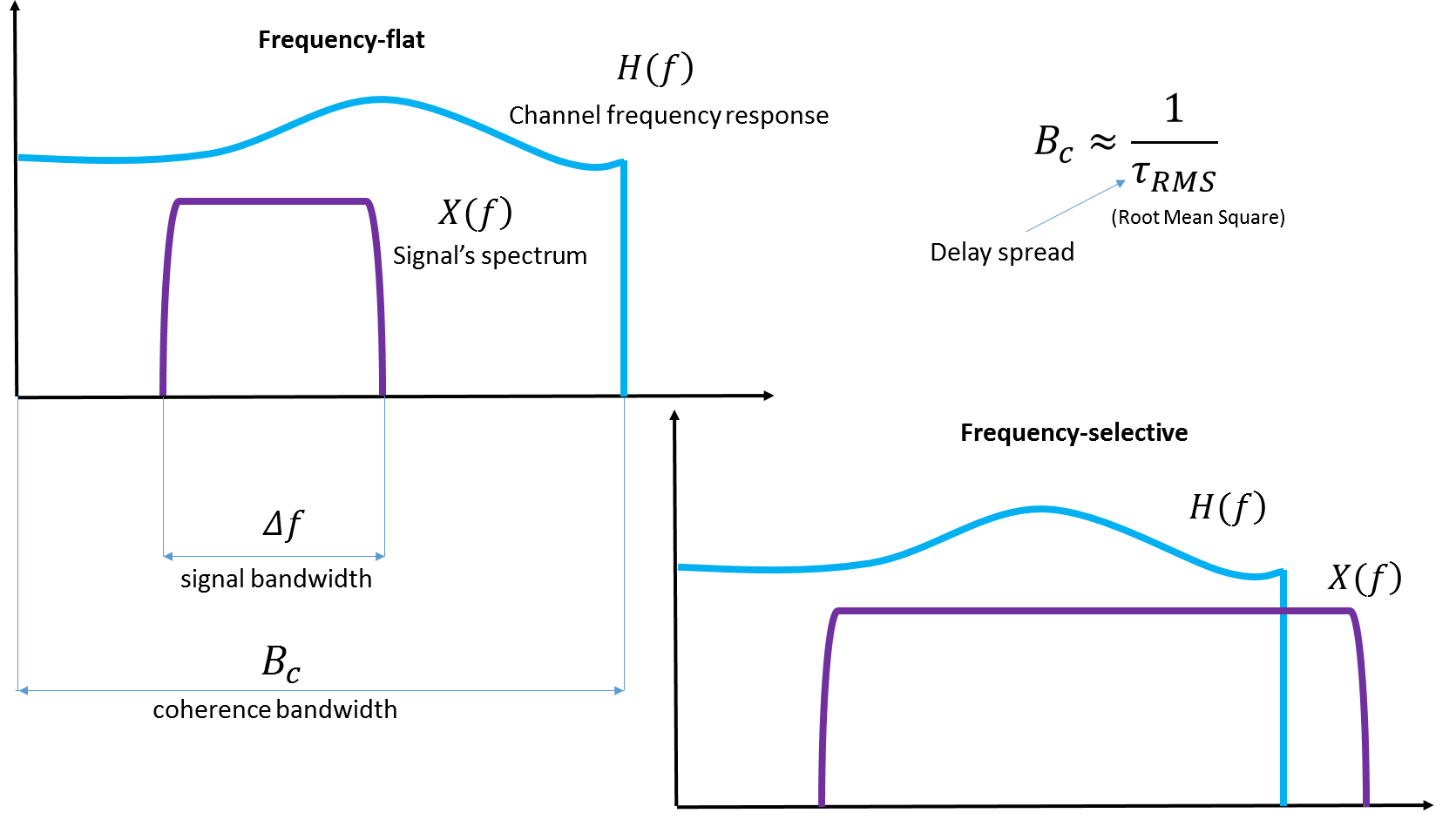
Fig. 4. Ilustración de ancho de banda coherente. Creo que no será una mala idea adjuntar ilustraciones de Wiki , si él mismo las agregó allí.

Preste atención a la extensión de retardo variable: la propagación de retrasos. Es esta extensión en retrasos entre la llegada de diferentes copias de la misma señal que se mide cuando se determinan las características de un canal real particular.

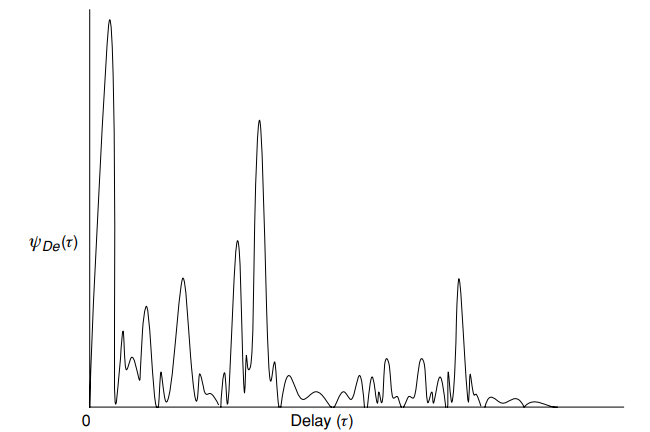
Fig. 5. Perfil típico de retraso (potencia) $\ psi_ {De} (\ tau)$ - potencia media en función del retraso $\ tau$ [1, p. 16]

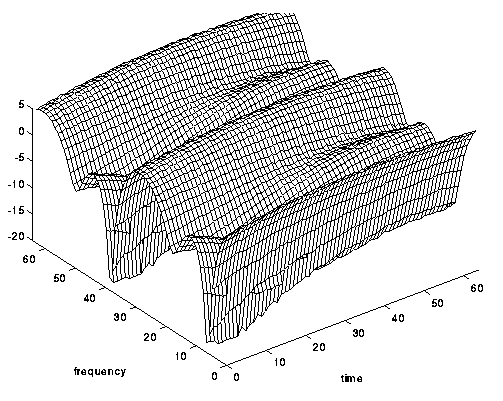
Fig. 6. Canal selectivo en frecuencia, pero no en tiempo .

Para cada rango, la banda coherente será diferente.

Por ejemplo, para la banda S (estaba interesado cuando buscaba información sobre sistemas satelitales) Bc = 0.5 - 2 MHz (Kanatas AG, Panagopoulos AD (ed.). Propagación de ondas de radio y modelado de canales para sistemas Tierra - Espacio. - CRC Press, 2016 . - p. 107).

Esto se ajusta muy bien a la velocidad en baudios de , por ejemplo, un transceptor de satélite de este tipo . Y no hay nada sorprendente: la tasa de símbolos de los tipos lineales de modulación digital (PSK, QAM, OFDM) coincide con la banda ocupada por la señal (ver Goldsmith A. Comunicaciones inalámbricas . - Universidad de Stanford, 2004. - p. 140, 326), lo que significa Sería bueno tratar de exprimir la señal en la banda coherente al máximo. Las frecuencias siguen siendo un recurso valioso.

En segundo lugar, si la longitud de nuestra señal en el dominio del tiempo excede el tiempo de coherencia del canal , entonces dicen que estamos tratando con un canal que varía en el tiempo.

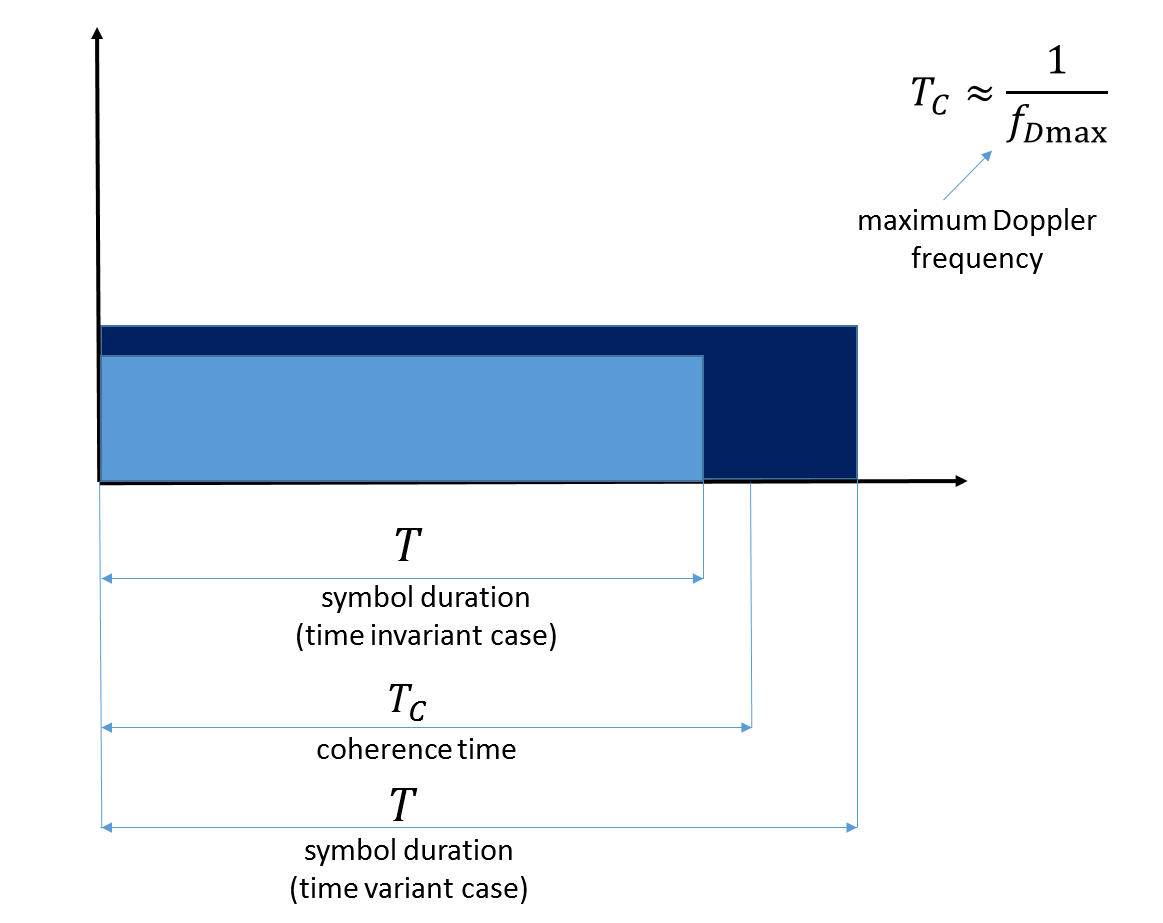
Fig. 7. Ilustración del tiempo de coherencia. Tenga en cuenta que aquí la frecuencia Doppler máxima refleja el movimiento del terminal móvil en sí.

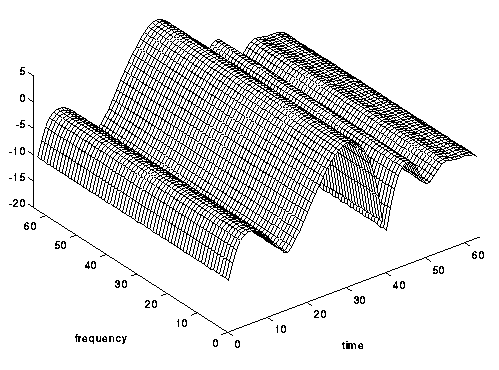
Fig. 8. Casi invisible en el tiempo, pero selectivo en el tiempo: un canal que decae rápidamente.

En la vida real, desafortunadamente, uno debe esperar ambos.

Canal de Rayleigh selectivo en tiempo y frecuencia; "La situación real".

Fuente de ilustración: tecnología inalámbrica Gigabit

Bueno, y en consecuencia, si logramos evitar de alguna manera lo anterior, entonces llegaremos al caso más simple y conveniente: desvanecimiento plano [1, p. 14-18] [2, pág. 88-92].

El canal de desvanecimiento más fácil

Es posible que ya haya visto una forma similar de simular un canal plano con desvanecimiento en alguna parte:

h = (1/sqrt(2))*(randn(size(msg)) + 1j*randn(size(msg))) % MatLab / Octave

Lo que se quiere decir:

falta de línea de visión (un caso justificado para comunicaciones terrestres)
canal de banda estrecha (canal de banda estrecha): encaja en la banda coherente
- Por cierto, consideramos un ejemplo de un canal de banda ancha en este artículo (Fig. 4).
tampoco hay selectividad de frecuencia: encaja en el tiempo coherente
falta de sombreado y cambios de frecuencia Doppler

Es decir, aquí está en persona: un canal plano con desvanecimiento . Para un caso sin línea de visión, el canal también se llama Rayleigh .

Lord Rayleigh

¿De qué viene ese modelo?

Primero, hablando de sistemas de comunicación modernos, lo más probable es que nos referimos a trabajar con señales digitales. Además, también estamos trabajando muy probablemente con tipos de modulación en cuadratura ( I / Q ), es decir, con señales complejas.

Fig. 9. La constelación de señales QPSK . Coordenadas polares, unidad de círculo. Por ejemplo, el símbolo 11 corresponderá a una coordenada igual a aproximadamente 0.7 + 0.7i .

Es lógico asumir el efecto de la interferencia tanto en el componente real como en el imaginario. Además, vale la pena seguir el Teorema del límite central para asumir también la naturaleza gaussiana de tales efectos. Escribimos la fórmula [1, p. 39]:

$Z = X + jY \ qquad (1)$

donde $X \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ y $Y \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ Se distribuyen normalmente variables aleatorias.

Muy a menudo, se usa un modelo con una potencia promedio normalizada:

$var \ {Z \} = E \ {\ left | Z \ derecha | ^ 2 \} = 1 \ qquad (2)$

Y eso significa $Z \ sim \ mathcal {N} (0, \, 1)$ .

Si asumimos distorsiones independientes de los componentes de la envolvente de la señal: tanto en fase ( I - En fase) como en cuadratura ( Q - Cuadratura), entonces la posición del número por el cual se multiplicará el símbolo original (de ahí el ruido multiplicativo ), en coordenadas polares puede ser calculado literalmente por el teorema de Pitágoras:

$Z = \ sqrt {\ hat {X} ^ 2 + \ hat {Y} ^ 2} \ qquad (3)$

donde $\ hat {X} \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ y $\ hat {Y} \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ - estas también son variables aleatorias normalmente distribuidas. Para potencia nominal $\ hat {X} \ sim \ mathcal {N} (0, \, 1)$ , $\ hat {Y} \ sim \ mathcal {N} (0, \, 1)$ .

¡Y aquí tenemos la fórmula del proceso de Rayleigh ! [2, p. 78]

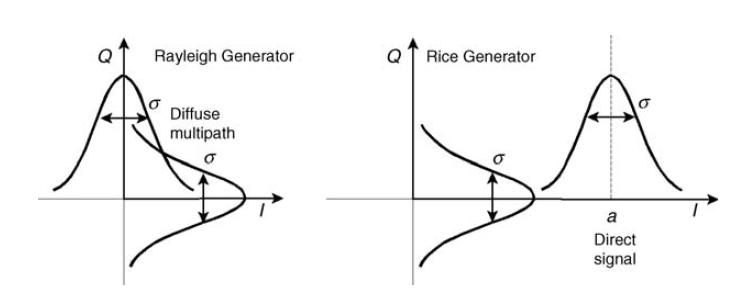
Fig. 10. Generadores cuadrados gaussianos para modelar el desvanecimiento de Rayleigh y Rice [3, p.125]. Hablaremos sobre el canal Rice un poco más tarde.

Digresión lírica.

Personalmente, me gusta mucho el ejemplo con disparos de cañones : si dos pistolas disparan perpendiculares entre sí un número suficiente de veces, entonces para cada individualmente la distribución de golpes será normal, y la distribución total de golpes es Rayleigh. Algo similar está sucediendo con nuestra interferencia.

Si consideramos el caso más simple sin ninguna correlación espacial entre los canales (digamos que tenemos varios canales espaciales, MIMO ), entonces dicen que el canal es espacialmente blanco, espacialmente blanco . Y como todos los canales son independientes, por lo tanto, es posible "generar" no solo variables aleatorias distribuidas de acuerdo con Rayleigh, sino también vectores, matrices y tensores [3, p. 125]:

$\ mathbf {H} _ {NLoS} = \ sqrt {\ frac {1} {2}} \ left (\ mathbf {G} _1 + j \ mathbf {G} _2 \ right) \ qquad (4)$

donde $\ mathbf {G} _1 \ sim \ mathcal {N} (0, \, 1)$ y $\ mathbf {G} _2 \ sim \ mathcal {N} (0, \, 1)$ Son matrices que consisten en valores normalmente distribuidos.

¿De dónde vino 1/2 debajo de la raíz?

Aquí todo es bastante simple: como dijimos anteriormente, el poder de respuesta del canal debe ser igual a la unidad, es decir:

$P = E \ {hh ^ * \} = 1$

Es por esto que se introduce el factor de escala $\ sqrt {\ frac {1} {2}}$ .

Demuestre (tome Python para variar):

 import numpy as np N = int(1e6) h = 1/np.sqrt(2)*(np.random.randn(N) + 1j*np.random.randn(N)) P = np.mean(h*np.conj(h)) print(np.round(P)) >>> (1+0j)

Para resumir :
El componente de interferencia en ausencia de visibilidad directa puede describirse como un vector n-dimensional (dependiendo de la dimensión del canal) independiente idénticamente distribuido ( IID - independiente idénticamente distribuido) de acuerdo con la compleja ley gaussiana con simetría circular y cero mat. expectativa ( ZMCSCG - números gaussianos complejos simétricos circulares de media cero).

¡Un trabalenguas entero!

Casi el canal de desvanecimiento más fácil

Bueno, ¿y si todavía hay visibilidad directa? ¿Quizás ya hay modelos matemáticos ya preparados para este puntaje?

Por supuesto que lo hay! Por ejemplo, esto [4] , generalizado para el caso con varias antenas de recepción y transmisión (MIMO):

$\ mathbf {H} = \ sqrt {\ frac {K} {K + 1}} \ mathbf {H_ {LoS}} + \ sqrt {\ frac {1} {K + 1}} \ mathbf {H_ {NLoS} } \ qquad (5)$

donde $$ \ mathbf {H}$ - esta es en realidad la envoltura compleja de la respuesta al impulso del canal (o matriz del canal, si estamos hablando de MIMO ), $$ \ mathbf {H_ {LoS}}$ Es un componente de visibilidad directa (Line-of-Sight), y $\ mathbf {H_ {NLoS}}$ - este es un componente de la falta de visibilidad directa (sin línea de visión), ya lo hemos considerado.

Preste atención a la variable K , este es el llamado factor de Rice (factor de Rician / Ricean) , la relación entre la potencia de la ruta de propagación directa y la potencia de todas las demás rutas. Es él quien determina cuánto nuestro canal estará sujeto a interferencia.

Stephen O. "Steve" Rice

Plazo $\ sqrt {\ frac {K} {K + 1}} \ mathbf {H} _ {LoS} = E \ {H \}$ representa la expectativa matemática de la matriz de canales y puede modelarse en función de la geometría de las matrices de antenas receptoras y transmisoras:

$\ mathbf {H} _ {LoS} = \ mathbf {a} _R (\ theta_R) \ mathbf {a} _T (\ theta_T) ^ H \ qquad (6)$

donde $\ mathbf {a} _R (\ theta_R)$ y $\ mathbf {a} _T (\ theta_T)$ - estas son las respuestas de las matrices de antenas receptoras y transmisoras, respectivamente, y $\ theta_R$ y $\ theta_T$ Son los ángulos de llegada y salida (ángulo de salida).

Los factores son generalmente simétricos y se pueden describir mediante la fórmula general:

$\ mathbf {a} = \ left [1, e ^ {j2 \ pi d cos (\ theta)}, ..., e ^ {j2 \ pi d (N-1) cos (\ theta)} \ right] \ qquad (7)$

donde $d$ Es la distancia entre antenas (espaciado de antena) en longitudes de onda, y $N$ - este es el número de elementos en la matriz de antenas (Fig. 11).

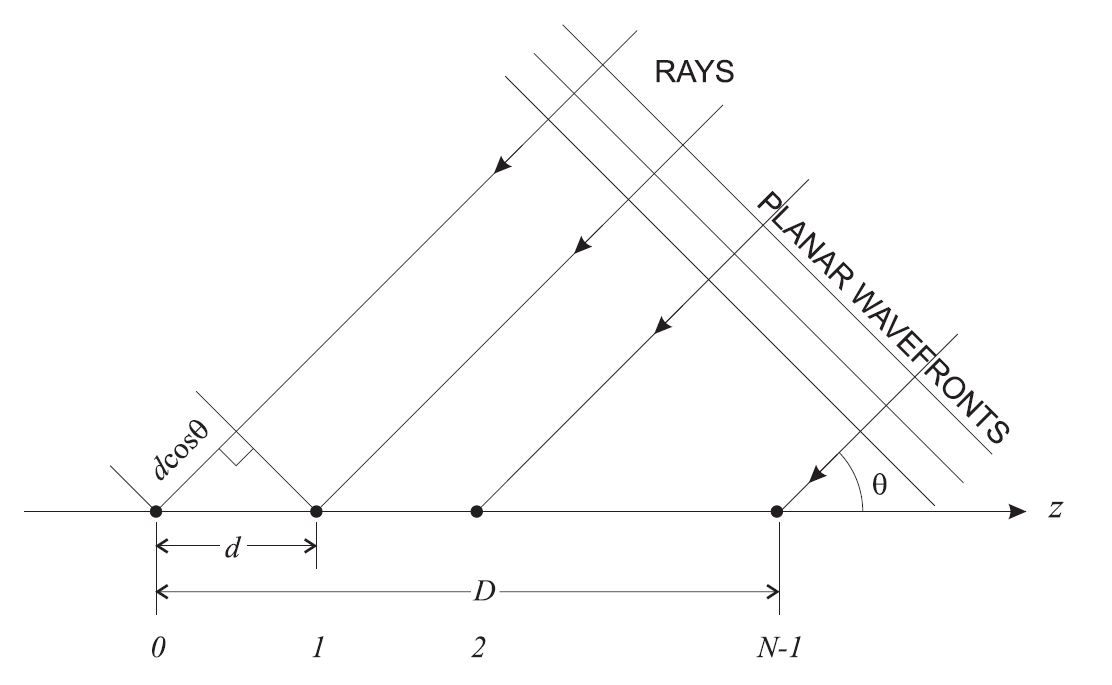
Fig. 11. La geometría de una matriz lineal . Para Massive MIMO, la geometría, por supuesto, será diferente. Puede leer más sobre esto, por ejemplo, aquí .

Bueno, ahora que el modelo está al menos algo desarmado, puedes simplificarlo.

Para el caso de SISO (el más simple y más básico), la fórmula (5) tomará la forma:

$h = \ sqrt {\ frac {K} {K + 1}} + \ sqrt {\ frac {1} {2 (K + 1)}} \ left (G_1 + jG_2 \ right) \ qquad (8)$

para 1 antena transmisora y 1 antena receptora $\ mathbf {a} _T (\ theta_T) \ mathbf {a} _R (\ theta_R) = 1$ .

Y esto, por cierto, se ajusta al modelo de la Figura 12.

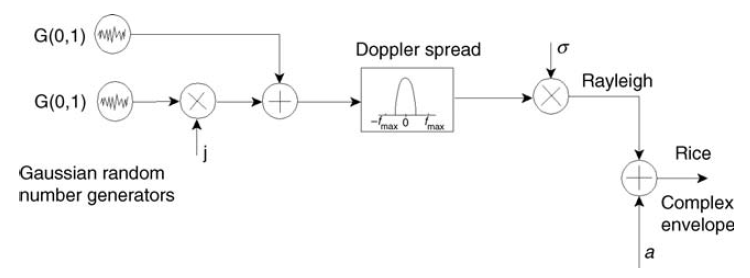
esquema

Fig. 12. El esquema de formación del canal de Rice (señal de banda estrecha) [3, p.127]. En $K \ a 0$ el canal degenerará más y más en Rayleigh. Es por eso que usé la palabra casi en el subtítulo: el canal Rayleigh es un caso especial del canal Rice. Esto también se ve en la fórmula (5).

Déjanos explicarte: $\ sigma = \ sqrt {\ frac {1} {2 (K + 1)}}$ Es el parámetro de escala de Rician, y $a = \ sqrt {\ frac {K} {K + 1}}$ Es un parámetro de no centralidad.

Si consideramos el desvanecimiento plano, se supone que el bloque Doppler Spread tiene una respuesta de 1.

En general, con el propósito de modelar Doppler Spread, lo más probable es que te encuentres con un modelo de Jakes (forma de U) basado en la técnica de suma de sinusoides . Teóricamente, el espectro de tal modelo se ve así:

La densidad espectral de potencia de la atenuación de Rayleigh con un desplazamiento Doppler máximo de 10 Hz. Fuente

Sin embargo, en la vida, a juzgar por [1, p. 15] tal espectro aún se ve menos parejo:

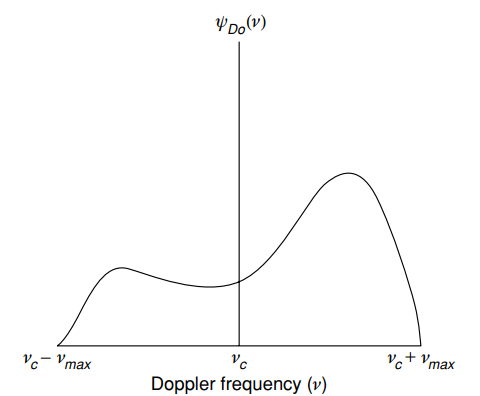
Espectro típico de Doppler (energía) $\ psi_ {Do} (v)$ - potencia media en función de la frecuencia Doppler $(v)$ [1, p. 15]

Expectativas ... Realidad.

Existen tales esquemas para combinar con desvanecimiento lento.

Por ejemplo, esto es para el modelo Corazza-Vatalaro (C y V) :

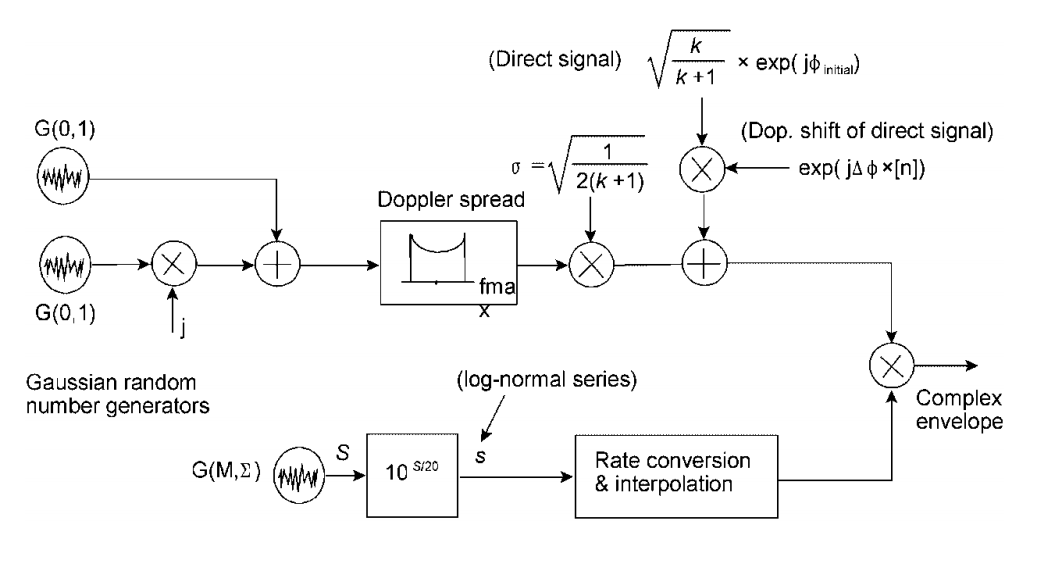
ver Fontan, FP, Mayo, A., Marote, D., Prieto - Cerdeira, R., Mariño, P., Machado, F., y Riera, N. (2008). Revisión de modelos generativos para el canal de propagación de satélite móvil terrestre de banda estrecha. Revista Internacional de Comunicaciones por Satélite y Redes, 26 (4), 291-316.

Pero esta es una historia completamente diferente ...

Modelando casi el canal de desvanecimiento más fácil en MatLab

Comparemos los cálculos recibidos con algo ya verificado. Por ejemplo, con funciones especiales de MatLab .

Para probar el modelo, por nuestra parte, generamos un mensaje binario aleatorio (la longitud del mensaje es de 100,000 bits), lo modulamos utilizando M-PSK o M-QAM , multiplicamos elemento por elemento el proceso de desvanecimiento, agregamos ruido gaussiano blanco, ecualizamos el ecualizador de fuerza cero, demodulamos y calculamos bit error ratio (BER - bit error ratio) (Fig. 13). El número de pruebas será igual a cien.

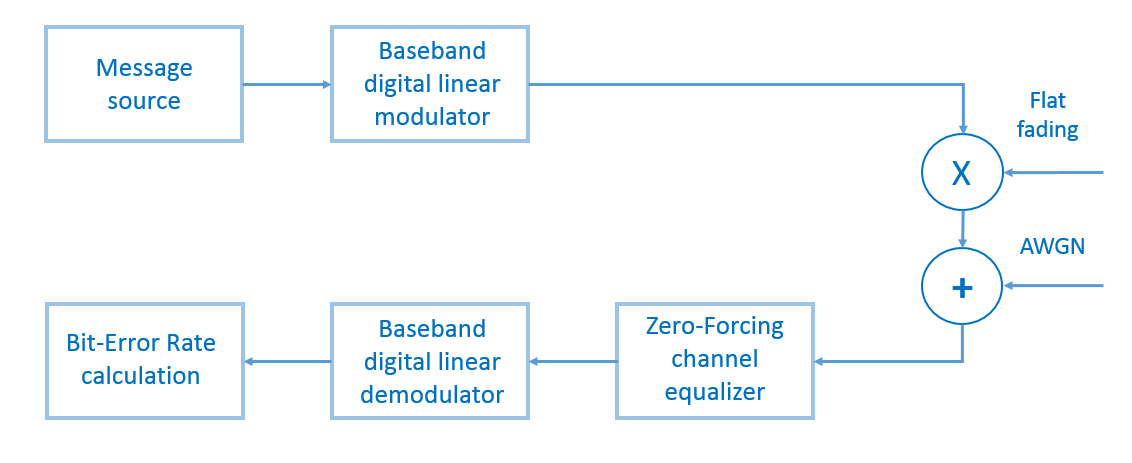
Fig.13. El diagrama de bloques del modelo del sistema de transmisión que describirá nuestro script.

El guión se puede ver aquí.

Y descárgalo aquí .

 clear all; close all; clc EbNo = 0:40; K = [4.0; 0.6]; M = [4; 8; 16; 64; 256]; %Positions of modulation (M-PSK or M-QAM) for k = 1:length(K) for m = 1:length(M) message = randi([0, M(m)-1], 100000, 1); if M(m) >= 16 mod_msg = qammod(message, M(m), pi/4, 'gray'); ric_ber(:, m, k) = berfading(EbNo,'qam',M(m),1,K(k)); else mod_msg = pskmod(message, M(m), pi/4, 'gray'); ric_ber(:, m, k) = berfading(EbNo, 'psk', M(m), 1, K(k)); end Es = mean(abs(mod_msg).^2); No = Es./((10.^(EbNo./10))*log2(M(m))); h = sqrt( K(k)/(K(k)+1)) +... sqrt( 1/(K(k)+1))*(1/sqrt(2))*(randn(size(mod_msg))... + 1j*randn(size(mod_msg))); ric_msg = mod_msg.*h; % Rician flat fading for c = 1:100 for jj = 1:length(EbNo) noisy_mod = ric_msg +... sqrt(No(jj)/2)*(randn(size(mod_msg))+... 1j*randn(size(mod_msg))); %AWGN noisy_mod = noisy_mod ./ h; % zero-forcing equalization if M(m) >= 16 demod_msg = qamdemod(noisy_mod, M(m), pi/4, 'gray'); else demod_msg = pskdemod(noisy_mod, M(m), pi/4, 'gray'); end [number,BER(c,jj)] = biterr(message,demod_msg); end end sum_BER(:,m, k) = sum(BER)./c; end end figure(1) semilogy(EbNo, sum_BER(:,1,1), 'b-o', EbNo, sum_BER(:,2,1), 'r-o',... EbNo, sum_BER(:,3,1), 'g-o', EbNo, sum_BER(:,4,1), 'c-o',... EbNo, sum_BER(:,5,1), 'k-o',... EbNo, ric_ber(:,1,1), 'b-', EbNo, ric_ber(:,2,1), 'r-',... EbNo, ric_ber(:,3,1), 'g-', EbNo, ric_ber(:,4,1), 'c-',... EbNo, ric_ber(:,5,1), 'k-', 'LineWidth', 1.5) title('Rician model (K = 4.0)') legend('QPSK(simulated)', '8-PSK(simulated)',... '16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',... 'QPSK(theory)','8-PSK(theory)', '16-QAM(theory)',... '64-QAM(theory)' ,'256-QAM(theory)','location','best') xlabel('EbNo (dB)') ylabel('BER') grid on figure(2) semilogy(EbNo, sum_BER(:,1,2), 'b-o', EbNo, sum_BER(:,2,2), 'r-o',... EbNo, sum_BER(:,3,2), 'g-o', EbNo, sum_BER(:,4,2), 'c-o',... EbNo, sum_BER(:,5,2), 'k-o',... EbNo, ric_ber(:,1,2), 'b-', EbNo, ric_ber(:,2,2), 'r-',... EbNo, ric_ber(:,3,2), 'g-', EbNo,ric_ber(:,4,2), 'c-',... EbNo, ric_ber(:,5,2), 'k-','LineWidth', 1.5) title('Rician model (K = 0.6)') legend('QPSK(simulated)', '8-PSK(simulated)',... '16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',... 'QPSK(theory)','8-PSK(theory)',... '16-QAM(theory)', '64-QAM(theory)' ,'256-QAM(theory)','location','best') xlabel('EbNo (dB)') ylabel('BER') grid on

Deberías obtener algo como esto:

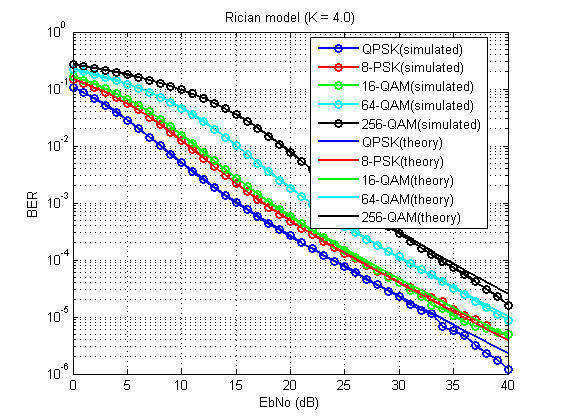
Fig. 14. El coeficiente de errores de bit para el modelo considerado (K = 4.0).

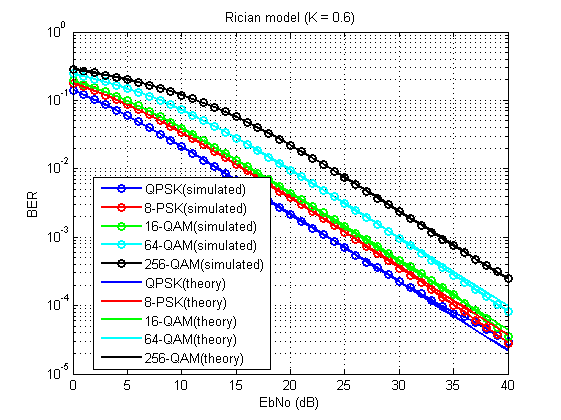
Fig. 15. Tasa de error de bit para el modelo considerado (K = 0.6).

No sin fallas, por supuesto (debido al número limitado de promedios), pero en general, ¡se puede ver que funciona!

Ok, pero ¿será posible escalar el experimento al caso de MIMO? Si por supuesto.

Para hacer esto, hacemos una suposición: la matriz de canales consistirá en rutas de propagación independientes, cada una de las cuales se distribuirá de acuerdo con Rice.

¿En qué condiciones es esto posible?

Como señalamos anteriormente, el IID del componente se puede generar en cualquier dimensión. Esto significa que cualquier canal MIMO espacialmente blanco sin línea de visión puede modelarse como un conjunto de canales SISO (dependiendo de la dimensión del canal).

Con el componente de la línea de visión un poco más complicado, debe tener en cuenta la posición de las rejillas.

Considere la fórmula (5): si nuestra matriz del componente de línea de visión consistirá solo de unidades $\ mathbf {H} _ {LoS} = \ mathbf {1}$ , parece que el componente Raysov también se vuelve espacialmente blanco.

Para abordar esto, escribimos el componente de la línea de visión con más detalle que en la fórmula (6):

$\ mathbf {H} _ {LoS} = \ begin {bmatrix} 1 \\ \ exp (j2 \ pi dcos (\ theta_R)) \\. \\. \\. \\ \ exp (j (M_R-1) 2 \ pi dcos (\ theta_R)) \ end {bmatrix} \ begin {bmatrix} 1 & \ exp (j2 \ pi dcos (\ theta_T)) &. &. &. & \ exp (j (M_T-1) 2 \ pi dcos (\ theta_T)) \ end {bmatrix}$

Llama la atención que si $\ theta_R = \ theta_T = 90 ^ o$ , entonces la matriz consistirá en una unidad. Geométricamente, esta es una situación en la que dos conjuntos de elementos están orientados estrictamente el uno al otro:

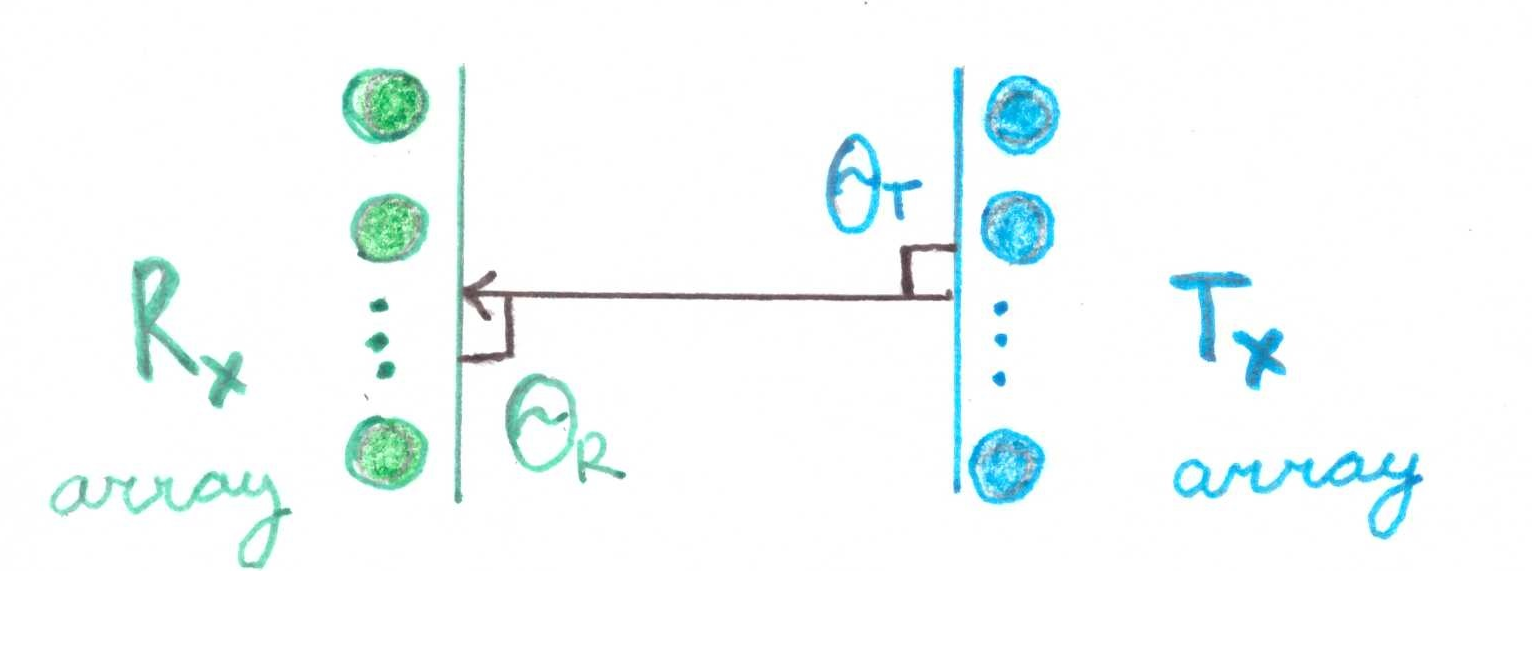
Hagamos una pequeña demostración matemática:

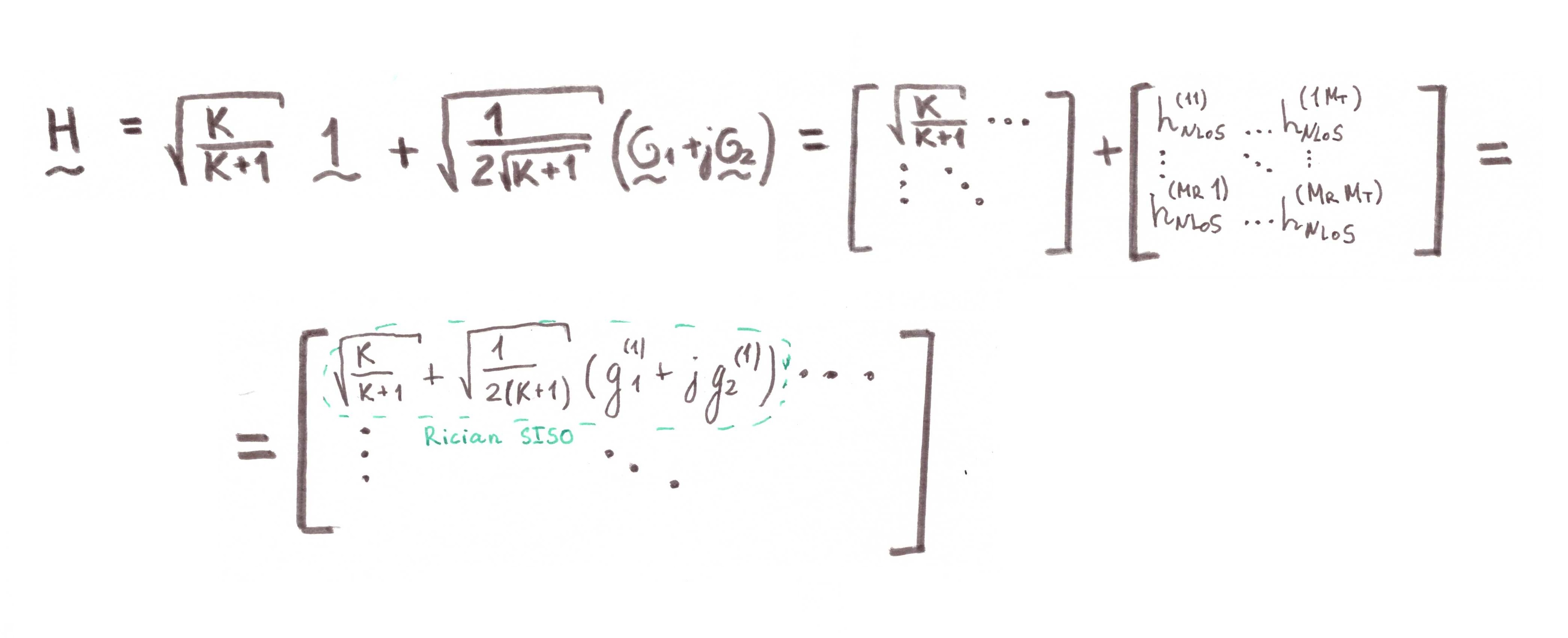
Para el modelado, tomamos como base el esquema de Alamouti . Debería resultar algo como esto:

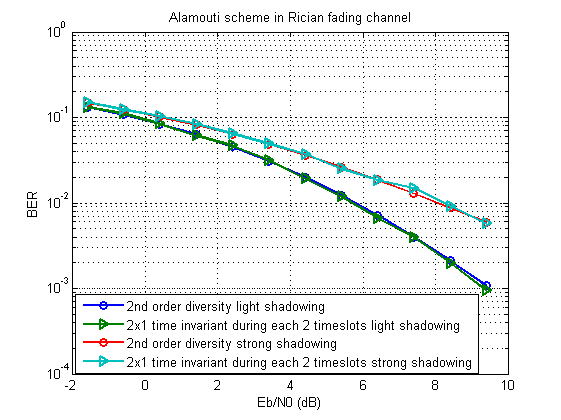
El script extendido se puede descargar aquí .

Bien hecho

Casi el canal de desvanecimiento más fácil y la correlación espacial

Y ahora, completando nuestro viaje al mundo de los cálculos estadísticos, acerquémonos un poco más a la realidad.

Arriba, consideramos el caso cuando el componente de la falta de línea de visión era espacialmente blanco . Sin embargo, de los sistemas reales aún se debe esperar cierta correlación entre las antenas y, por lo tanto, entre las rutas de propagación de la onda EM.

Introducimos una nueva variable: la matriz de correlación espacial:

$\ mathbf {R} = E \ {vec (\ mathbf {H}) vec (\ mathbf {H}) ^ H \} \ qquad (8)$

donde vec denota una operación de vectorización . Por cierto, esta matriz solo afectará el componente de la falta de línea de visión y, por lo tanto, en este caso $\ mathbf {H} = \ mathbf {H} _ {NLoS}$ .

Ejemplo para MIMO 2x2

Es razonable suponer que en la vida real, esta matriz se determina primero a través de mediciones, y solo luego se utilizan para modelar:

$vec (\ mathbf {H} _ {NLoS}) = \ mathbf {R} ^ {1/2} vec (\ mathbf {H} _w) \ qquad (9)$

donde $\ mathbf {H} _w$ Es la matriz IID ( w significa espacialmente blanco).

Tenga en cuenta que elevar una matriz a una potencia no es elevar a una potencia de cada uno de sus elementos. Por lo tanto, en nuestro caso, la función sqrt () no se puede usar en MatLab . Usa el operador ^ .
En el caso de Python, no puede usar el operador de exponenciación ** y el método sqrt del popular módulo numpy . Debe usar el método fraccional_matriz_poder del módulo scipy .

Si el receptor y el transmisor son suficientemente independientes entre sí, como en la Figura 16, entonces se puede aplicar el modelo Kronecker [1, p. 40], para reducir el número de coeficientes para el cálculo:

$\ mathbf {R} = \ mathbf {R} ^ T_T \ otimes \ mathbf {R} _R \ qquad (10)$

donde $\ otimes$ denota un trabajo de Kronecker .

Leopold Kronecker

Consideramos por separado los componentes de la matriz de expresión:

$\ mathbf {R} _R = \ frac {1} {M_T} E \ left \ {\ left (\ mathbf {H} _ {NLoS} \ mathbf {H} ^ H_ {NLoS} \ right) ^ T \ right \ }$ Es la matriz de correlación de las antenas receptoras,

$\ mathbf {R} _T = \ frac {1} {M_R} E \ left \ {\ mathbf {H} ^ H_ {NLoS} \ mathbf {H} _ {NLoS} \ right \}$ Es la matriz de correlación de antenas de transmisión.

$M_R$ y $M_T$ - este es el número de antenas de recepción y transmisión, respectivamente. Ambas matrices son matrices Hermitianas positivas semi-definidas. Además, el rango de la matriz $\ mathbf {H} _ {NLoS}$ limitado por valor $min (rango (\ mathbf {R} _T), rango (\ mathbf {R} _R))$ .

Fig. 16)
Modelo de difusores en el caso de receptor y transmisor no correlacionados. Los puntos verdes significan difusores, el azul y el rojo significan receptor y transmisor. Pido disculpas por la calidad, esta es una captura de pantalla de una de las tareas de TU Ilmenau.

La matriz de canales en este caso se puede escribir como:

$\ mathbf {H} = \ sqrt {\ frac {K} {K + 1}} \ mathbf {H} _ {LoS} + \ sqrt {\ frac {1} {K + 1}} \ mathbf {R} ^ {1/2} _R \ mathbf {H} _ {w} \ left (\ mathbf {R} ^ {1/2} _T \ right) ^ H \ qquad (11)$

Sin embargo, para situaciones como, por ejemplo, en la Figura 17, aún debe usar la matriz de correlación completa (consulte la fórmula (9)).

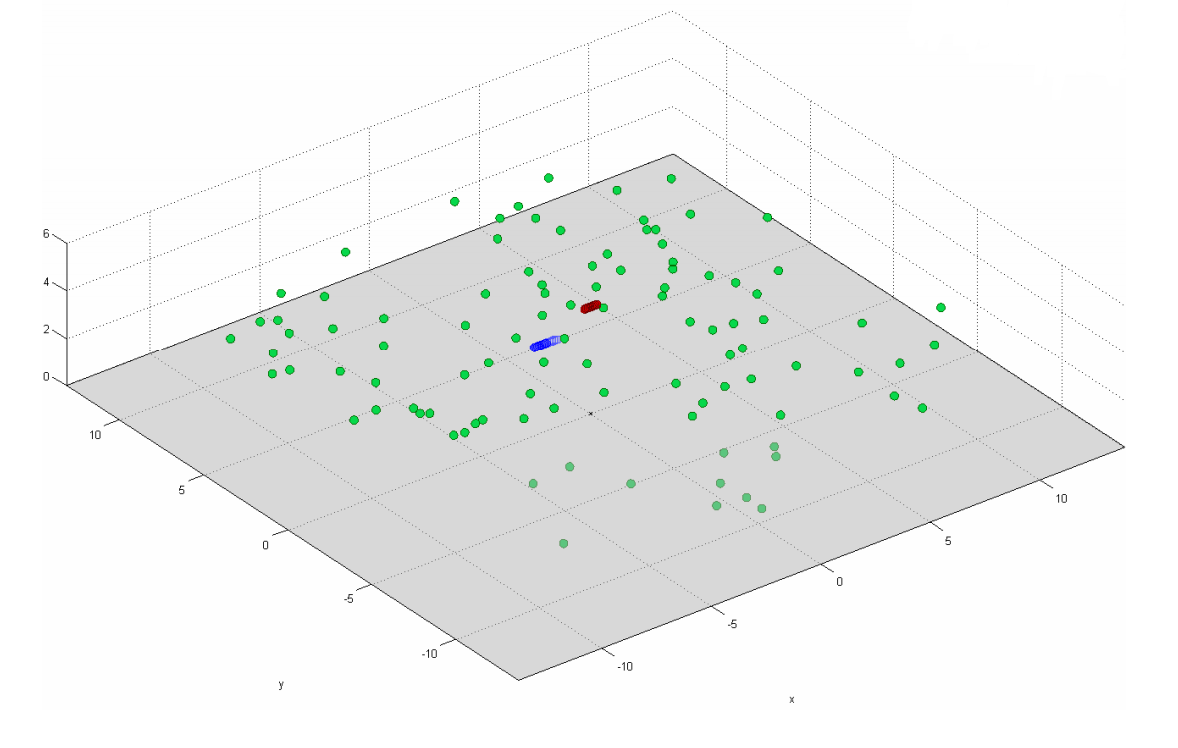
Fig. 17. Modelo de difusores en el caso de correlación de receptor y transmisor. Los puntos verdes significan difusores, el azul y el rojo significan receptor y transmisor.

Para consolidar lo que hemos aprendido y ver cómo la correlación espacial complica la vida, intentemos calcular el ancho de banda de los canales. Por ejemplo, para MIMO 2x2.

Para hacer esto, tomamos los siguientes casos (nos referimos al mismo desvanecimiento plano, por simplicidad también consideramos solo el canal de Rayleigh):

1) Canal espacialmente blanco;
2) Modelo de Kronecker con una correlación relativamente débil:

$\ mathbf {R} _T = \ mathbf {R} _R = \ begin {bmatrix} 1 y 0.4 \\ 0.4 y 1 \ end {bmatrix}$

3) Modelo de Kronecker con una correlación relativamente fuerte:

$\ mathbf {R} _T = \ mathbf {R} _R = \ begin {bmatrix} 1 y 0.6 \\ 0.6 & 1 \ end {bmatrix}$

Usaremos Python 3.4 en esta parte. La función para calcular el ancho de banda se tomará de una de mis publicaciones anteriores .

 import numpy as np from numpy import linalg as LA import matplotlib.pyplot as plt from scipy.linalg import fractional_matrix_power def openloop_capacity(H_chan, SNR_dB): SNR = 10**(SNR_dB/10) Mt = np.shape(H_chan)[1] H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H) lambdas = LA.eigvals(H_sq) lambdas = np.sort(lambdas)[::-1] c = 0 for eig in lambdas: c = c + np.log2(1 + SNR*eig/Mt) return np.real(c)

Defina los principales parámetros del sistema:

 Mr = 2 # number of receive antennas Mt = 2 # number of transmit antennas Rr1 = np.array([[1., .4], [.4, 1.]]) # case 1 Rr2 = np.array([[1., .6], [.6, 1.]]) # case 2 Rt1 = np.array([[1., .4], [.4, 1.]]) # case 1 Rt2 = np.array([[1., .6], [.6, 1.]]) # case 2 Rr1_half = fractional_matrix_power(Rr1, 0.5) Rr2_half = fractional_matrix_power(Rr2, 0.5) Rt1_half = fractional_matrix_power(Rt1, 0.5) Rt1_half_H = np.conj(Rt1_half).T Rt2_half = fractional_matrix_power(Rt2, 0.5) Rt2_half_H = np.conj(Rt2_half).T

Comenzamos la simulación:

 counter = 1000 SNR_dBs = [i for i in range(1, 21)] C_MIMO_uncorr = np.empty((len(SNR_dBs), counter)) C_MIMO_kron1 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron2 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron3 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron4 = np.empty((len(SNR_dBs), counter)) for c in range(counter): H_uncorr = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2) H_kron1 = np.dot(Rr1_half, np.dot(H_uncorr, Rt1_half_H)) H_kron2 = np.dot(Rr2_half, np.dot(H_uncorr, Rt2_half_H)) for idx, SNR_dB in enumerate(SNR_dBs): C_MIMO_uncorr[idx, c] = openloop_capacity(H_uncorr, SNR_dB) C_MIMO_kron1[idx, c] = openloop_capacity(H_kron1, SNR_dB) C_MIMO_kron2[idx, c] = openloop_capacity(H_kron2, SNR_dB) C_MIMO_uncorr_erg = np.mean(C_MIMO_uncorr, axis=1) C_MIMO_kron1_erg = np.mean(C_MIMO_kron1, axis=1) C_MIMO_kron2_erg = np.mean(C_MIMO_kron2, axis=1)

Dibujo

 plt.figure(figsize=(7, 5), dpi=100) plt.plot(SNR_dBs, C_MIMO_uncorr_erg,'g-o', label='Uncorrelated') plt.plot(SNR_dBs, C_MIMO_kron1_erg, 'm-o', label='Kronecker model, case 1') plt.plot(SNR_dBs, C_MIMO_kron2_erg, 'r-o', label='Kronecker model, case 2') plt.title("Rayleigh flat fading (MIMO 2x2)") plt.xlabel('SNR (dB)') plt.ylabel('Ergodic capacity (bps/Hz)') plt.legend() plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()

Obtenemos:

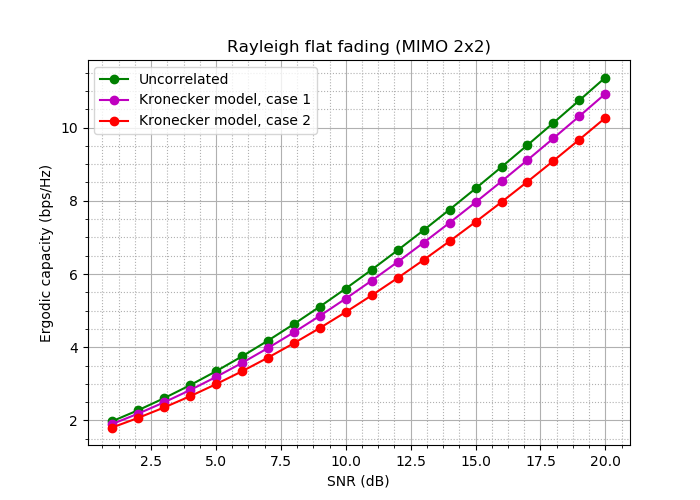
Fig. 18. Curvas de ancho de banda para estos experimentos.

Bueno: la diferencia, aunque no es crítica, es!

Epílogo

Quizás uno de los lectores haya notado que casi todo lo que examinamos hoy (en detalle y de pasada) es bastante bueno en los parámetros del objeto de comunicación matlab comM.MIMOChannel . Este hecho me parece muy importante:

en primer lugar, sistematiza aún más lo descrito anteriormente,
y, en segundo lugar, enfatiza que estamos abordando los problemas actuales.

Bueno, y ahora, si usas tales bloques, entonces espero que quede más claro por qué y qué plumas necesitas girar.

¡Gracias a todos por su atención!

Agregaré aquí un enlace a las diapositivas sobre el tema de Reiner S. Thomä (Ilmenau), sobre el cual nos dio conferencias en ese momento. ¡Creo que alguien será útil!

Literatura

Paulraj, Arogyaswami, Rohit Nabar y Dhananjay Gore. Introducción a las comunicaciones inalámbricas espacio-temporales. Cambridge University Press, 2003.
Goldsmith A. Comunicaciones inalámbricas. - Cambridge University Press, 2005.
Fontæn, Fernando Pærez y Perfecto Mariæo Espiæeira. Modelado del canal de propagación inalámbrico: un enfoque de simulación con Matlab. Vol. 5. John Wiley & Sons, 2008.
Farrokhi, Farrokh R., y col. "Eficiencia espectral de los sistemas inalámbricos FDMA / TDMA con conjuntos de antenas de transmisión y recepción". Transacciones IEEE en comunicaciones inalámbricas 1.4 (2002): 591-599.

Casi el canal MIMO más fácil con desvanecimiento (modelo Kronecker incluido)