Fractales en números irracionales. Parte 2

Parte 0: Fractales en números primos.
Parte 1: Fractales en números irracionales.



El artículo contiene imágenes GIF y contrastantes. Los epilépticos pueden tener una crisis epiléptica.

En un artículo anterior, vimos un algoritmo de visualización de secuencia binaria. Recordemos

Toma la secuencia binaria. Como ejemplo, los primeros bits de una secuencia fractal discutidos en un artículo anterior:

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

0100110110010011001001101100

Dibujamos un campo de celda cuadrada. Establecemos los bits en el límite superior. La distancia entre los bits es de dos celdas:



Para cada bit, dibuje un camino discontinuo a lo largo de la diagonal (a través de la celda). Para ceros, dibuja el primer trazo a la derecha:



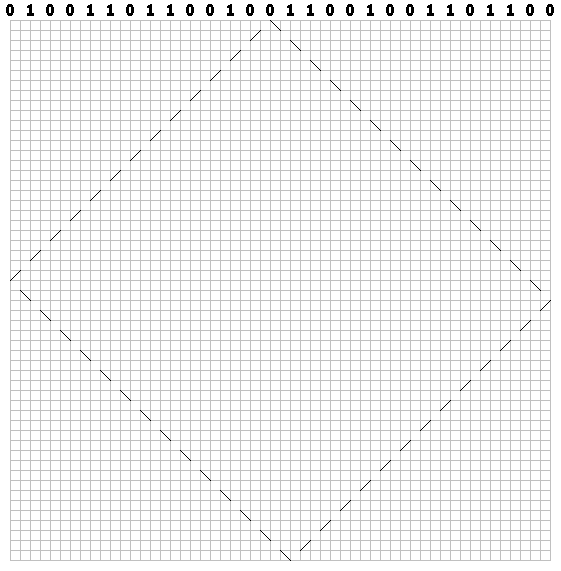
Para unidades - a la izquierda:



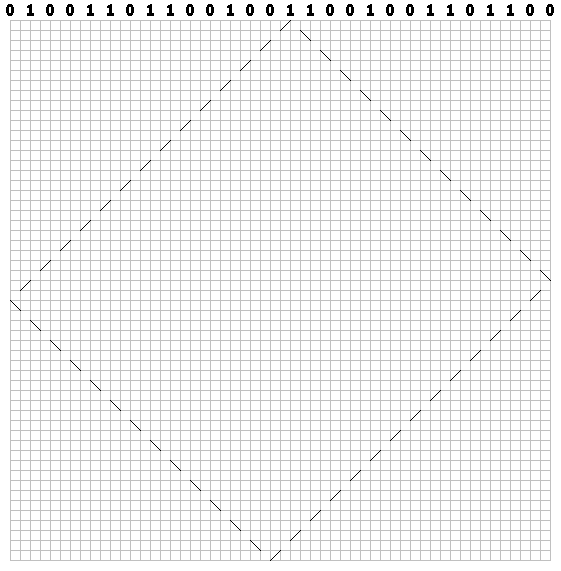
Dibuja una trayectoria para cada bit. Tenemos un patrón de "billar":



Se puede obtener un patrón idéntico (sin un defecto a lo largo de la diagonal: la secuencia es infinita, lo visualizamos como una secuencia final) de otra manera. Invierta cada bit par en la secuencia:

0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0 0 1 1 1 0 0 1

A continuación, para cada bit, dibuja líneas discontinuas verticales:



Ponemos los bits a la izquierda, dibujamos líneas horizontales:



Combinamos:



Después de escribir el primer artículo, dos preguntas quedaron sin resolver:

1. ¿Es posible dibujar un patrón fractal para números irracionales? Usted puede El problema se resolvió en un artículo anterior. En la imagen de arriba, parte del patrón fractal para $$$\ sqrt {2}$. Si selecciona una de las curvas en este patrón:



Obtenga la conocida curva fractal: "Fibonacci word fractal".

2. La segunda pregunta es si es posible escribir un algoritmo que pinta un patrón:



La segunda cuestión se abordará en este artículo. Colorearemos los patrones con la ayuda de un telar, cuyo trabajo simulamos usando JavaScript.



En el diagrama de arriba, la máquina más fácil. Consiste en dos marcos a través de los cuales se estiran los hilos. Los marcos están conectados a los pedales. Cuando presiona uno de los pedales, uno de los cuadros se eleva. Los hilos dibujados a través de este marco se elevan y un hilo transversal se estira en el espacio resultante entre los hilos. Si estira los hilos pares e impares a través de diferentes cuadros, obtendrá un tejido en un patrón de tablero de ajedrez:



En máquinas más complejas, se utilizan cuatro o más marcos:


Telar de mesa Ashford de 4 ejes

Para no confundirse qué pedal presionar, hacen un diagrama.



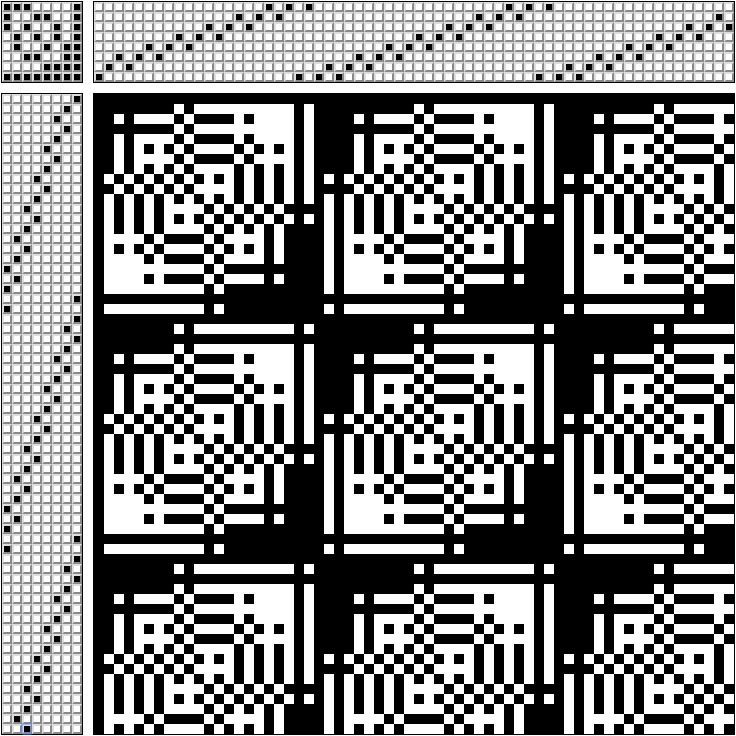
En la parte superior derecha del patrón, se indica a través de qué cuadros van los hilos (patrón para un telar de 8 cuadros).

En la esquina superior izquierda: qué pedales se deben sujetar al mismo tiempo (cada pedal está conectado solo con su propio cuadro).

En la parte inferior izquierda, en qué orden pedalear.

En la parte inferior derecha, qué tejido obtenemos. Si estira el hilo blanco a través del negro, obtenemos un patrón monocromo.

Inmediatamente "entrar" el principio puede parecer un poco difícil. La siguiente imagen muestra cómo se forma el patrón de tejido:



Escribamos un guion. Estiraremos los hilos a través de los marcos utilizando la matriz unidimensional array2. En la matriz unidimensional array1, escribimos la secuencia de sujeción del pedal. En array3 (matriz binaria 8x8) escribimos qué pedales se deben sujetar al mismo tiempo.

for(var i=0;i<length;i++){ for(var j=0;j<length;j++){ if(array3[array1[i]][array2[j]]){ context.fillRect(i, j, 1, 1); } } } 

Script (funciona en Google Chrome).

Con la ayuda de nuestro telar improvisado podemos dibujar una amplia variedad de patrones:



Pero históricamente, la persona promedio no tiene más de dos piernas. Por lo tanto, es conveniente sujetar simultáneamente no más de dos pedales. Uno de los patrones más populares para un telar es el siguiente:



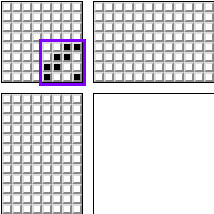
Para 4 cuadros. Y su modificación para 8 cuadros:



Inesperadamente, los patrones (o un fragmento de patrones) realizados con esta plantilla son similares a nuestros patrones de "billar". Además, estos patrones están sombreados:



Puedes aprender a seleccionar patrones de "billar" para un telar. Un ejemplo:



Al comienzo del artículo, ya vimos un fragmento de este patrón.

Termine con telares y escriba un guión para visualizar secuencias binarias. Podemos deshacernos de una de las matrices: el patrón es simétrico en diagonal. ¿Cómo llenar la matriz restante? Elemental:



Tomamos la secuencia para $$$\ sqrt {2}$. Crea una matriz. En el elemento cero de la matriz, escriba el bit cero de la secuencia. Alternativamente, tome cada bit de la secuencia. Si el enésimo bit = 1 - escriba en la matriz a [n] = a [n-1] +1. Si bit = 0 - escriba a [n] = a [n-1] -1

$$

$$Q_n = \ lfloor n \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ... \\ a_n = \ begin {cases} a_ {n-1} +1, Q_n = 1; \\ a_ {n-1} -1, Q_n = 0 \ end { casos}$$

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } 

Comprobamos:

  for(var i=0;i<size;i++){ context.fillRect(i, a[i]+50, 1, 1); } 

De hecho, ya hemos recibido un fractal elemental, pero continuaremos.

A continuación, trataremos con la matriz:



Resumir $$$x$y $$$y$. Divida el módulo entre 4. Si el resultado resultante = 0 o 1 - escriba en la matriz verdadero. Para 2 y 3, escribe falso. Podemos prescindir de una matriz (no se sabe de antemano qué valores máximos y mínimos toma una [n]). Resume una [x] y una [y]. A la cantidad resultante, agregue algún número $$$C$(para deshacerse de esos casos cuando la cantidad es un número negativo). Divida el módulo entre 4. Para los valores 0 y 1, pinte sobre el píxel con coordenadas $$$x$y $$$y$.

El algoritmo final solo toma unas pocas líneas:

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } for(var x=0;x<size;x++){ for(var y=0;y<size;y++){ q=(a[x]+a[y]+512)%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); } } 

Visualiza nuestras secuencias fractales.

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Puede modificar fácilmente el script para obtener una imagen RGB:

  q=(a[x]+a[y]+512)%4; /*if(q==0 || q==1) context.fillRect(x, y, 1, 1);*/ if(q==0) context.fillStyle = 'rgb(255,0,0)'; if(q==1) context.fillStyle = 'rgb(0,255,0)'; if(q==2) context.fillStyle = 'rgb(0,0,255)'; if(q==3) context.fillStyle = 'rgb(0,0,0)'; context.fillRect(x, y, 1, 1); 

Arriba, agregamos un número a la suma a [x] + a [y] $$$C$. Si no agrega este número, el valor mínimo de la suma = -8, el máximo = 8 (para $$$x$y $$$y$de 0 a 750). Si quitas $$$C$- en algunos casos, la suma resulta ser negativa y no un múltiplo del cuarto y para estos casos el píxel no se pinta (permanece negro):

  q=(a[x]+a[y])%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); 

Puedes imaginarlo como si una parte del fractal estuviera debajo de un borde imaginario (debajo de este borde solo se pintan los valores negativos multiplicados por 4: -4, -8, -12, ...).

Podemos ver dónde está esta frontera:

  if(a[x]+a[y]>=0) context.fillRect(x, y, 1, 1); 

En lugar de dividir el módulo, podemos comparar la suma con un cierto valor específico y, por lo tanto, pintar sobre una sola "capa" del fractal. Como ejemplo, tome el promedio entre los valores mínimo y máximo:

  q=(a[x]+a[y]); if(q==0) context.fillRect(x, y, 1, 1); 

Cambiando los valores de mínimo a máximo, podemos ver cómo cambian las "capas" en la dinámica:




Además, podemos "en la frente" comparar una [x] con una [y] y también obtener un patrón fractal:

 if(a[x]==a[y]) context.fillRect(x, y, 1, 1); 

La siguiente secuencia:

$$

$$Q_n = \ lfloor n (\ sqrt {2} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractal:



RGB:



Capa media:



En dinámica:

$$

$$Q_n = \ lfloor n \ sqrt {3} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractal:



RGB:



Capa media:



En dinámica:

$$

$$Q_n = \ lfloor n (\ sqrt {3} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractal:



RGB:



Capa media:



En dinámica:

$$

$$Q_n = \ lfloor n \ sqrt {5} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

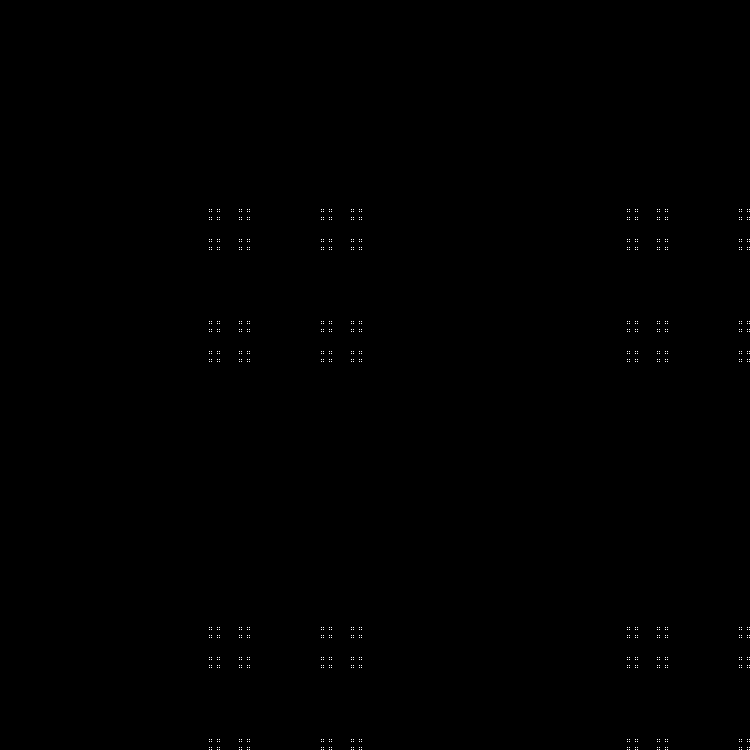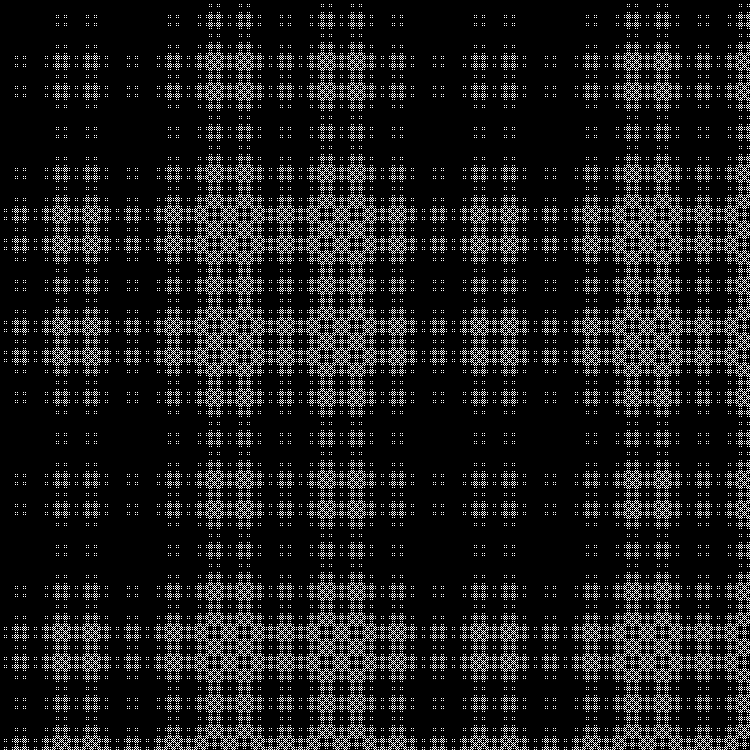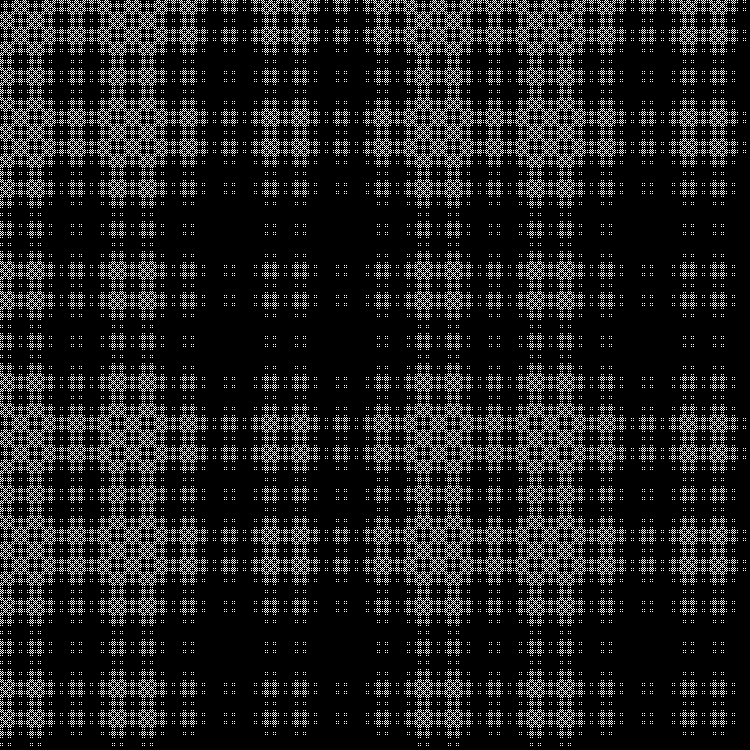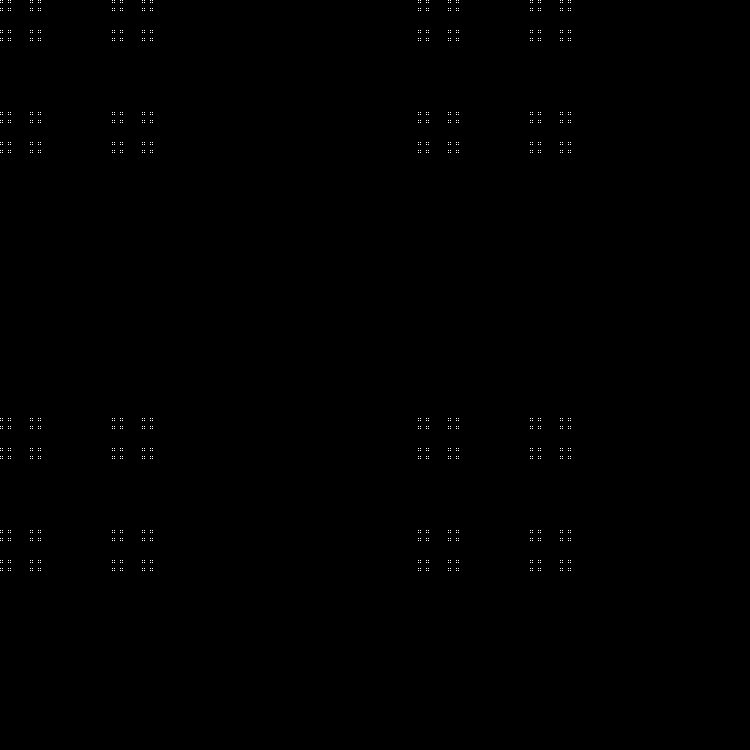
Fractal:



RGB:



Capa media:



En dinámica:



Bueno, nuestro fractal favorito (parte de este patrón se puede dibujar con billar, con tamaños de lados iguales a los números de Fibonacci):

$$

$$Q_n = \ lfloor n (\ sqrt {5} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractal:



RGB:



Capa media:



En dinámica:



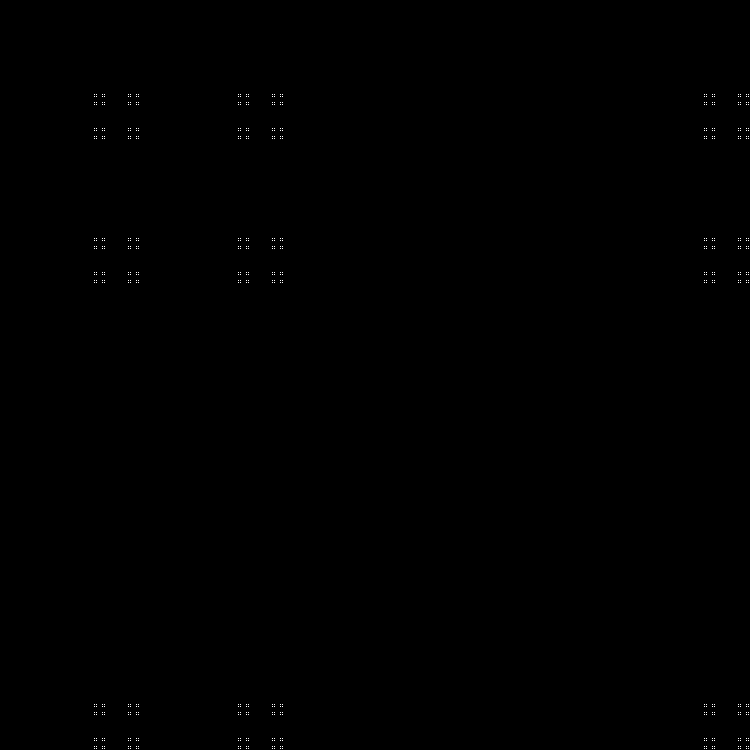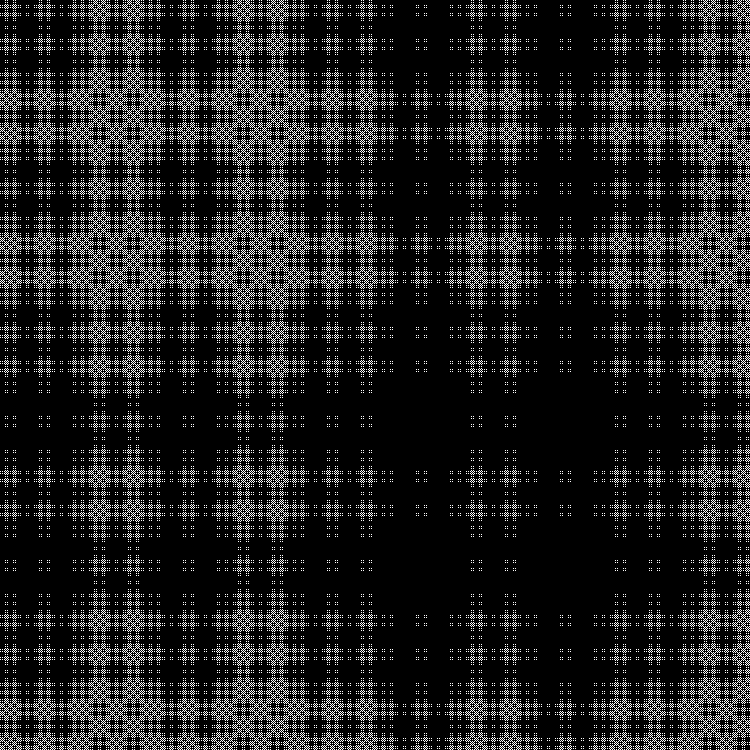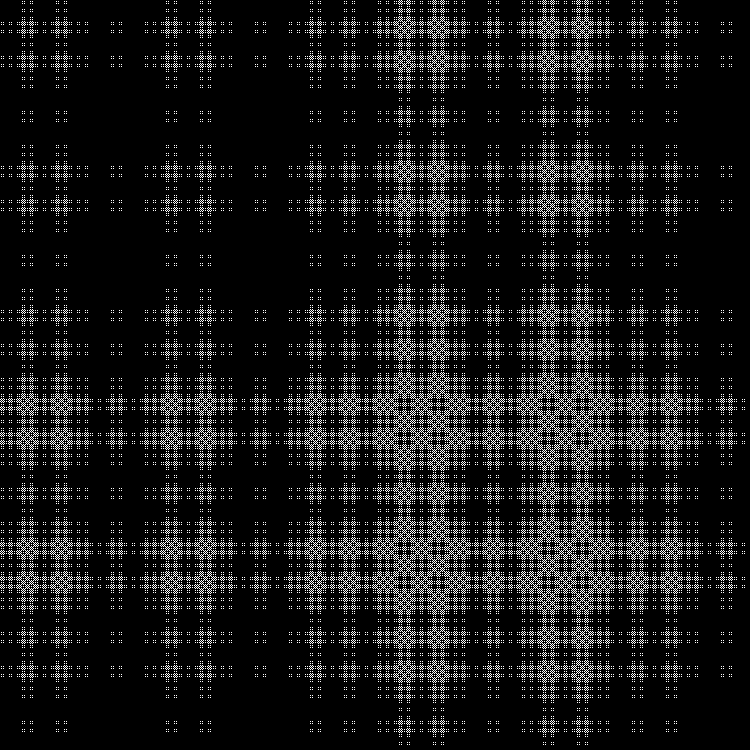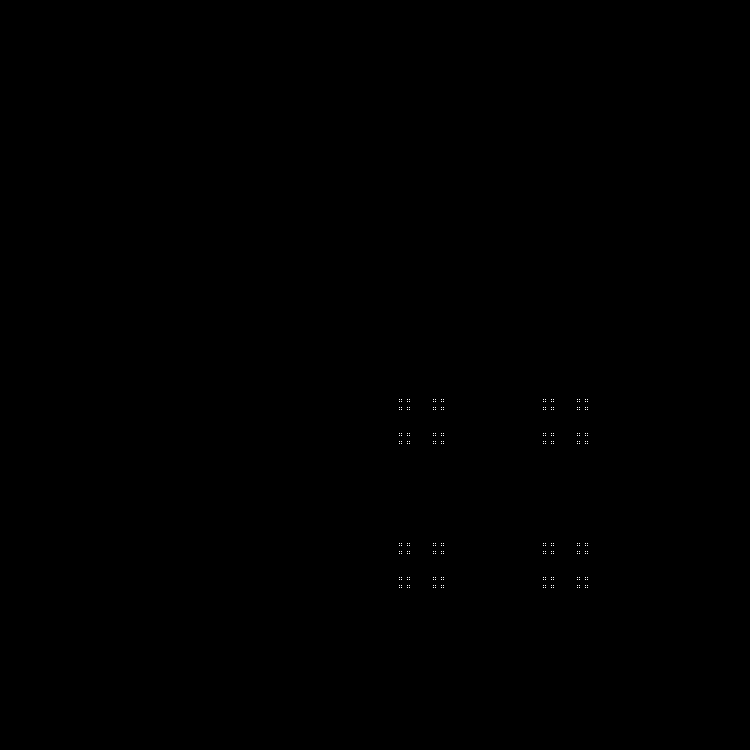
Otra secuencia para completar:

$$

$$Q_n = \ lfloor n ^ {2} \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Patrón:



RGB:



Capa media:



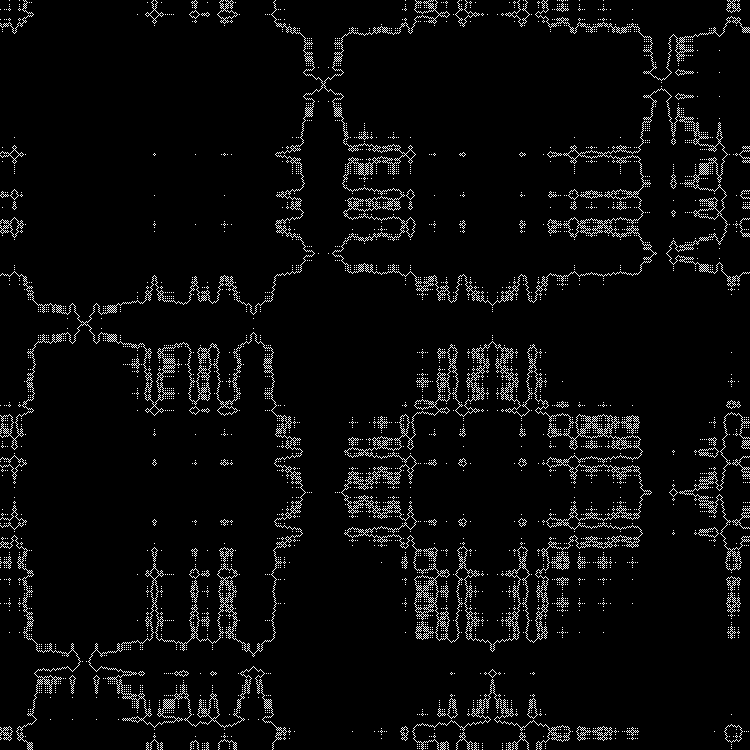
En dinámica:



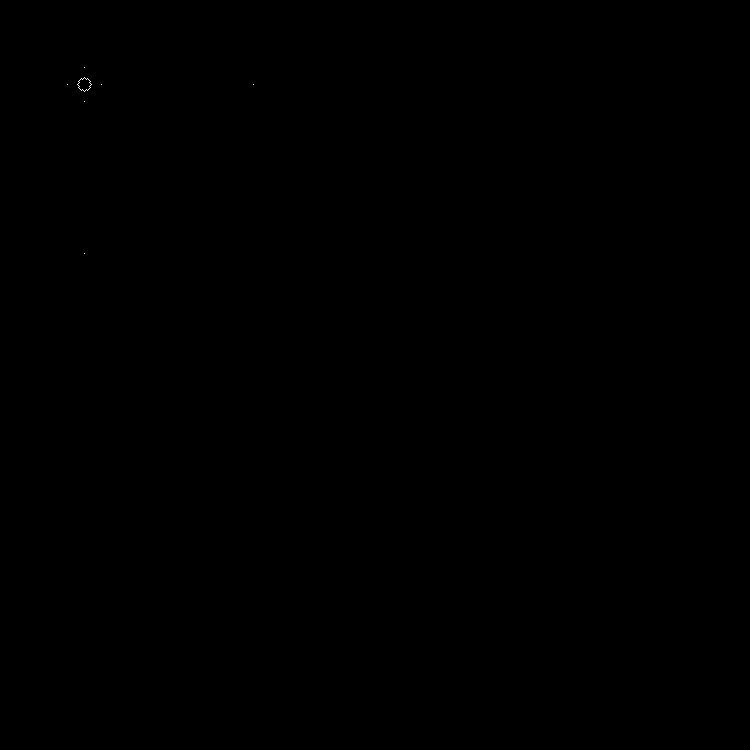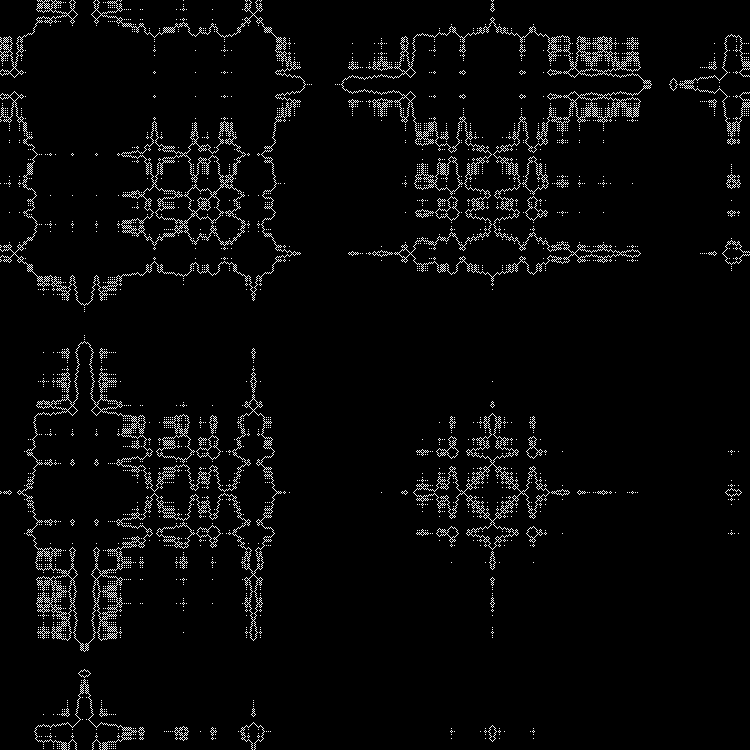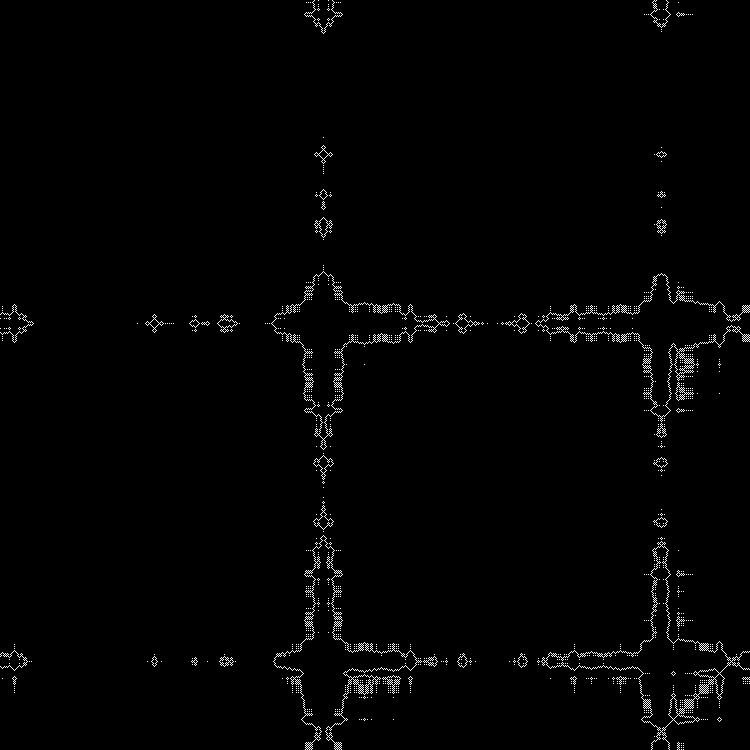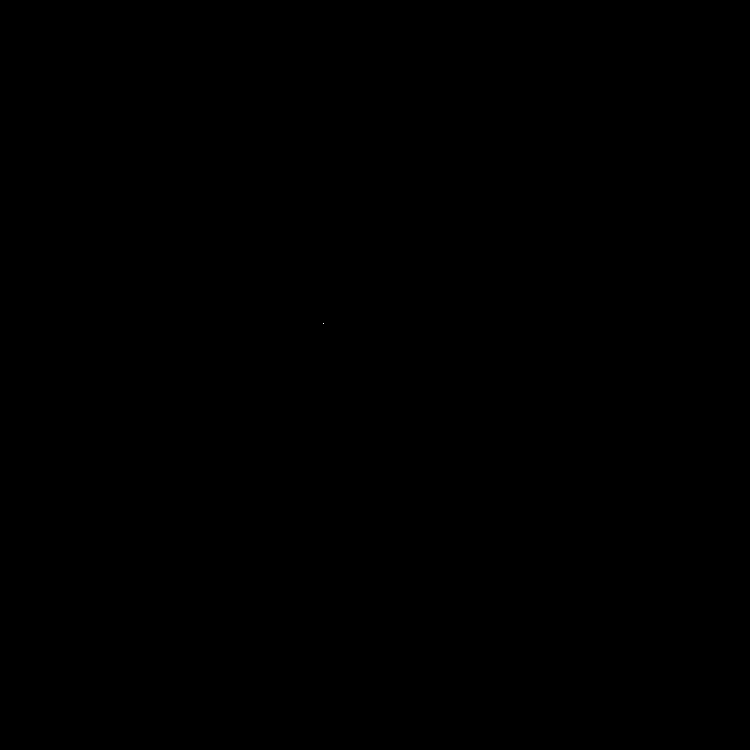
Se pueden introducir otras raíces cuadradas en el guión . (Puede conducir en valores fraccionarios).

En el segundo script, puede conducir la secuencia manualmente.

Otro guión para billar. Coordenadas del mouse: dimensiones de billar. El patrón de la izquierda se forma a partir de la secuencia obtenida utilizando el resto de la división (detalles en el artículo anterior). En el lado derecho - paridad $$$\ lfloor n \ frac {y} {x} \ rfloor$.