Introduccion

Sobre el proyecto

El proyecto "Tipo de cambio absoluto" se dedica al análisis de los tipos de cambio emparejados, la asignación de los tipos de cambio absolutos de ellos y su análisis. En el marco del proyecto, se obtuvo una metodología para la conversión de tasas de pares a tasas de cambio absolutas. Para esto, se define la moneda absoluta ABS. Todas las monedas disponibles se expresan en términos de ABS.

En el artículo "De pares de divisas a tipos de cambio absolutos" se ofrece una descripción detallada de la tecnología.

Sobre problema

Este artículo aborda el problema de un análisis cualitativo de la coherencia de los tipos de cambio.
La necesidad de estudiar la relación entre las monedas se debe a los requisitos para la selección de instrumentos financieros en la cartera de inversiones y la capacidad de predecir el comportamiento de las monedas en función de los datos de otras monedas asociadas a ellas.

Es recomendable incluir instrumentos con alta conectividad multidireccional en la cartera de inversiones. Esto le permite reducir el riesgo general de la cartera.

Y, si encuentra herramientas con un alto grado de conexión, en función del comportamiento de algunos, puede predecir el comportamiento de los demás.

Sobre el experimento

Selección de método

Como datos iniciales para el experimento, hay series de datos con tasas de cambio absolutas (ver archivo fuente. Hoja de "tasas de cambio absolutas" ).



Para estudiar la conectividad de una serie de datos numéricos, es mejor usar la correlación de Pearson (ver Correlación - Wikipedia ).

El coeficiente de correlación tiene un rango de valores de "-1" a "+1". Los valores negativos grandes indican una fuerte relación multidireccional. Los valores positivos grandes indican una fuerte conectividad unidireccional. La proximidad del coeficiente a "0" indica la ausencia de comunicación.

Que quieres conseguir

El propósito del experimento es obtener grupos de monedas con un alto grado de conexión. Además, el signo de la comunicación también es de interés.

Lugar

Todos los cálculos se llevarán a cabo en el sistema Wolfram Mathematica (ver Wolfram Mathematica - Wikipedia ). Y utilizaremos Wolfram.Cloud recursos gratuitos en la nube.

El recurso especificado le permite crear cuadernos en línea con cálculos y le permite proporcionar acceso para visualización general. El cuaderno de este experimento se encuentra aquí .

Plan

Realizaremos cálculos de acuerdo con el siguiente plan.

Primero, calculamos la matriz de correlación. Las columnas y filas de la matriz corresponderán a monedas individuales. En la intersección de la columna y la fila estará el coeficiente de correlación del par.

A continuación, seleccionamos pares de monedas con los lazos más fuertes. Coloque los pares seleccionados en el gráfico (ver Gráfico (matemáticas) - Wikipedia ).

Los nodos del gráfico son monedas. Los bordes del gráfico indicarán la relación entre las monedas. El color de la costilla indicará el signo de enlace. El verde indica una relación positiva y el rojo indica una relación negativa.

La secuencia de cálculos indicada se realizará tanto para cursos absolutos como para sus cambios. Un análisis de la relación de cursos absolutos le permite explorar procesos lentos (más de un día). Un análisis de la relación entre los cambios en los tipos de cambio absolutos nos permitirá investigar las rápidas conexiones entre monedas (un día).

Resultados

Profundidad de muestreo

El archivo fuente contiene datos de los últimos 150 días. Según ellos, se realizará el cálculo.

Nube de divisas

El experimento involucró 45 monedas.



Se puede ver una lista completa de monedas en la hoja "Resumen de divisas" del archivo fuente .

Correlación de tasa absoluta

Arriba (ver. Plan), se planeó calcular la matriz de correlación para tasas absolutas. El resultado se muestra en la imagen a continuación.



Aquí, el rojo corresponde a una conexión positiva y el azul a una conexión negativa. Para comprender, se da una escala de gradación. Debajo y a la izquierda están los tickers de moneda (nombres cortos).

Gráfico de dependencia de tasa absoluta

La matriz de correlación permitió distinguir dos grupos de monedas con un alto grado de conexión. Para hacer esto, se seleccionaron pares con una correlación superior a 0.9 y se transfirieron al gráfico.



El primer grupo reunió monedas con un alto grado de dependencia del dólar estadounidense. Aquí están las monedas de cuatro países árabes que comercian con petróleo, el dólar de Hong Kong y el propio dólar estadounidense. Todas las dependencias son positivas (unidireccionales).

El segundo grupo reunió monedas europeas. En el centro se encuentra el Euro y, a su alrededor, las monedas de Polonia, Rumania y Dinamarca. Todas las dependencias son positivas (unidireccionales).

Cambios relativos en tasas absolutas

Para futuras investigaciones, calculamos la serie de cambios relativos en las tasas absolutas. La fórmula para los cálculos es la siguiente.



La diferencia entre valores sucesivos se correlacionará con la anterior de los dos. Por lo tanto, recibiremos un cambio relativo en la tasa absoluta.

Correlación de cambios relativos en tasas absolutas

En cuanto a los cursos absolutos, obtenemos una matriz de correlación para mediciones relativas de cursos absolutos. Le damos una visualización gráfica de la matriz.



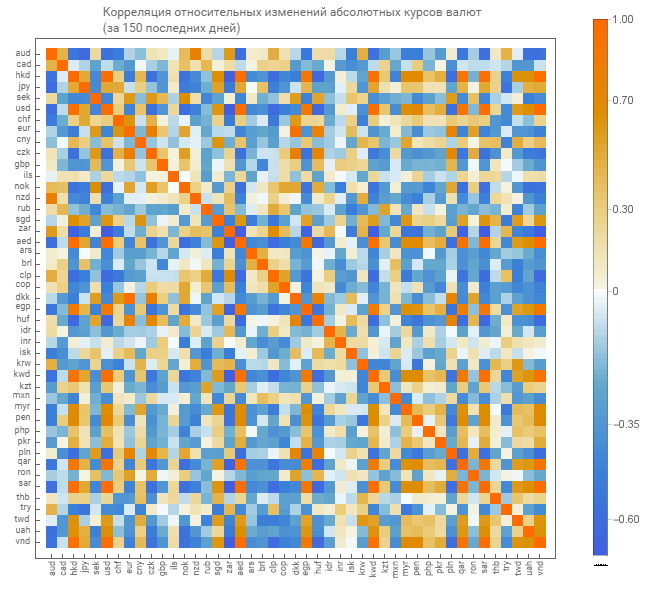
Ya hay una matriz de tonos más claros. Lo que indica un menor grado de conexión.

Gráfico de dependencia de cambios relativos en tasas absolutas

De la matriz de correlación de cambios relativos, seleccionamos pares de monedas con un alto grado de conexión. Solo el nivel de muestreo aquí ya es 0.6 (aquí y arriba, este coeficiente se eligió de la consideración de un pequeño número de pares para la salida al gráfico).



En el caso de cambios relativos recibimos 3 grupos de monedas. El grupo superior combinó las monedas de Australia y Nueva Zelanda. El grupo inferior reunió monedas europeas. El grupo medio alrededor del dólar de Hong Kong combinó las monedas de los Estados Unidos, Vietnam, cinco países árabes: exportadores de petróleo, Sudáfrica y Perú.

Además, hay una característica interesante en la alta dependencia negativa del rand sudafricano.

Conclusiones

Como resultado del experimento, logramos obtener lo siguiente.

Poner los datos de la matriz de correlación en un gráfico matemático es una buena práctica de visualización para la matriz de correlación. La aplicación adicional de este método simplificará la comprensión de las relaciones en el grupo de series de números.

Se encuentra un método formal para agrupar los mercados de divisas. Fue posible distinguir formalmente los mercados de Europa, América con Asia y Oceanía. Este método puede acortar significativamente el camino para revelar las influencias mutuas entre los mercados de diferentes países y convertirse en una buena herramienta para un analista financiero.

La inclusión del rand sudafricano en la cartera de inversiones junto con el dólar estadounidense reducirá los riesgos de dicha cartera.

Catalogo de articulos