Dado: 12 monedas, una de ellas es falsa, solo difiere en peso. Desconocido más ligero o más pesado. Se proporcionan escalas de apalancamiento que muestran que la carga en un lado es más pesada. Para 3 pesadas, necesitas encontrar una moneda falsa.
Por experiencia, le aconsejo que no se apure, que decida por escrito. El rompecabezas "12 monedas, 3 pesadas" surgió varias veces en mi vida. La primera vez que mi amiga me preguntó, ella decidió después de los Juegos Olímpicos y tuve que romperme la cabeza por un par de horas. Y unos años más tarde no me lo dieron de inmediato. Si quieres decidir por ti mismo, hazlo en un papel.
A continuación se presentarán un análisis y etapas de la solución. Las etapas se llevarán a cabo de acuerdo con una metodología universal para resolver problemas, aplicable tanto a la programación como a la vida. Con el enfoque, resolver el rompecabezas será fácil.
Te sugiero, antes de leer, ofrecer una solución. ¿Tienes una respuesta? Verificado?
Si se tratara de software, las preguntas serían: “¿Has programado y probado el algoritmo? ¿Ha examinado los casos de prueba y los ha verificado?
Como muestra la experiencia, para resolverlo es necesario dibujar un árbol de decisión y verificar los 12 casos.

1. ConsejosEn el proceso de resolución ayudará a:1) Disminución de la entropía (medidas de incertidumbre) y respuestas a las preguntas:
- ¿Qué aprendiste en el paso anterior?
- ¿Qué reduce la incertidumbre?
- ¿Qué información tenemos?
- ¿Qué más necesitas saber?
Las preguntas son adecuadas para cualquier tarea, proyecto. Las respuestas a ellos ayudan a reducir el riesgo de no cumplir con los plazos, los excesos de presupuesto y ponerse al día con los superiores.
2) Descomposición. El enfoque de lo simple a lo complejo. Si prepara una solución para los casos más simples y luego los usa para resolver el problema (dividir y conquistar el algoritmo), será más fácil que representar la situación en su cabeza.
Los algoritmos de dividir y conquistar dividen una tarea en dos o más subtareas del mismo tipo, pero de tareas más pequeñas a elementales, y combinan sus soluciones para obtener una respuesta al problema original.Componer preguntas para descomposición. ¿Cuál sugerirías?
2. Descomposición¿Qué preguntas formuló para la descomposición? Cualquier partido?
1) ¿Cuál es la situación más elemental? ¿Qué podemos hacer en una pesaje?
Para un pesaje podemos determinar qué moneda es más pesada, si el peso de las monedas es igual.
2) Si tenemos 2 monedas y, como saben, la falsificación es más difícil o más ligera. ¿Cómo determinar una falsificación en un pesaje?
Es necesario pesar las monedas y, dependiendo de la flecha de la balanza, determinar la falsificación.
3) Si tenemos 2 monedas y, no se sabe, la falsificación es más difícil o más fácil, ¿cómo se puede determinar la falsificación en un solo pesaje?
Después de pesar una de las 2 monedas presentadas con la tercera moneda, se sabe que es genuina.
4) Si tenemos 3 monedas y, como saben, la falsificación es más difícil o más ligera. ¿Cómo determinar una falsificación en un pesaje?
Es necesario comparar dos de estas monedas, si son iguales, la tercera moneda es falsa.
5) Si tenemos 3 monedas, y, se desconoce, la falsificación es más difícil o más fácil. ¿Es posible determinar una falsificación en un pesaje?
Lamentablemente no.
6) Si tenemos 4 monedas, y la falsificación desconocida es más difícil o más ligera, ¿podemos determinar la falsificación en un pesaje?
Lamentablemente no.
7) Si tenemos 4 monedas, y, se desconoce, la falsificación es más difícil o más fácil, ¿cuántas pesas se pueden determinar falsas?
Para dos pesajes.
A continuación, de casos elementales, recopilamos situaciones de 8, 9, 10, 11 y 12 monedas. ¿Cómo ves la solución?
A continuación se muestra la solución completa.
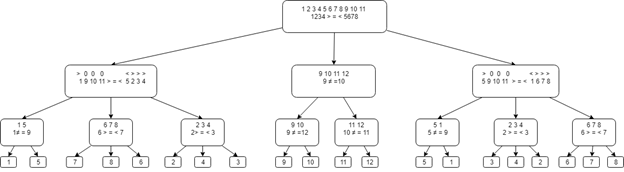
3. DecisiónPrimer paso: dividir las monedas en 3 grupos de 4: 1 2 3 4, 5 6 7 8, 9 10 11 12.
Compara los dos primeros grupos. Son posibles tres opciones:
- el primer grupo es más pesado;
- el segundo grupo es más pesado;
- son iguales

1) Si los grupos son iguales, entonces la moneda falsa está en el tercer grupo. Es necesario encontrar una moneda falsa de 4 monedas en dos pesadas.
Divida el tercer grupo en dos: 9 10 11 12
Compare 9 y 10:
- si son iguales, entonces la moneda falsa en el segundo grupo - compare 9 y 11. Si 9 y 11 son iguales, entonces la moneda falsa - 12, si no -11
- si no son iguales, entonces falso en el primer grupo - compare 10 y 12. Si 10 y 12 son iguales - falso - 9, si no - 10.
Entonces encontramos una moneda falsa.
2) Considere el segundo caso. Si el primer grupo es más pesado que el segundo, entonces asignamos al primer grupo el signo ">", al segundo grupo el signo "<", el tercer grupo - "0".
Dividimos las monedas en grupos 1 9 10 11 y 5 2 3 4, pesados. Son posibles tres opciones:
- Son iguales La moneda falsificada se encuentra entre los números: 6 7 8. Compare 6 y 7, si son iguales, la falsificación es 8, si 6 es mayor, la falsificación - 7, si 7 es mayor, la falsificación - 6, ya que en este caso la moneda falsificada es más fácil.
- El primer grupo es más pesado, luego la moneda falsa es 1 o 5. Compare 1 y 9 si son iguales - la moneda falsa - 5, si no - 1.
- El primer grupo es más fácil, luego falso entre las monedas 2 3 4, ya que se sabe que 9, 10 y 11 son reales, y el segundo grupo solo puede ser compensado por las monedas 2, 3 y 4. Compare 2 y 3, si son iguales, falso 4, si 2 es más pesado, entonces falso es 2, de lo contrario el tercero es falso.
3) El caso cuando el segundo grupo es más pesado que el primero es similar al segundo.
El diagrama general del Árbol de decisión se presenta a continuación.
ConclusiónCuando llega una tarea para revisión o depuración, es bueno aplicar el enfoque anterior:
- Decidir lo que se da?
- ¿Qué casos / tareas elementales se pueden descomponer?
- ¿Qué se desconoce para resolver el problema? ¿Qué experimentos se deben hacer para reducir la entropía?
- Corre
- ¿Se solucionó el problema? No? Regrese al paso 1.
Soluciones exitosas.