Estimación de VaR y ConVaR para el precio de las acciones de la empresa kazaja

En las últimas décadas, la economía mundial cae regularmente en este vórtice de crisis financieras que han afectado a cada país. Casi condujo al colapso del sistema financiero existente, debido a este hecho, todos los expertos en modelos matemáticos y económicos se han vuelto a utilizar métodos para controlar las pérdidas del activo y la cartera en el mundo financiero (Lechner, LA, y Ovaert, TC (2010). Existe una tendencia creciente hacia el modelado matemático de un proceso económico para predecir el comportamiento del mercado y una evaluación de su sostenibilidad (ibid.) Al no tener la atención necesaria para controlar y evaluar adecuadamente las amenazas, todo el mundo comprende que puede desencadenar tremendo costo en el desarrollo de la organización o incluso quiebra.

El Valor en Riesgo (VaR) eventualmente ha sido un enfoque regular para detectar el riesgo entre las instituciones del sector financiero y su regulador (Engle, R. y Manganelli S., 2004). El modelo se aplica originalmente para estimar el valor de pérdida en la cartera de inversiones dentro de un período de tiempo determinado, así como a una probabilidad de ocurrencia dada. Además del uso de VaR en el sector financiero, hay muchos ejemplos de evaluación de valor en riesgo en diferentes áreas, como anticipar al personal médico para desarrollar la gestión de recursos de atención médica Zinouri, N. (2016). A pesar de su primitividad aplicada en un experimento real, el modelo consiste en inconvenientes en la evaluación (ibid).

El objetivo del informe es una descripción del modelo VaR existente que incluye una de sus versiones de actualización, a saber, Valor condicional en riesgo (CVaR). En la siguiente sección y la sección 3, se explican el algoritmo de evaluación y las pruebas del modelo. Para una ilustración vívida, la pérdida esperada se estima en el activo de una de las empresas kazajas que cotiza en el mercado de valores financieros en un largo período de tiempo. Las secciones finales 4 y 5 discuten y demuestran los hallazgos del trabajo de investigación.

Antecedentes

Se cree que el primer uso del VaR por parte de las organizaciones financieras gigantes hasta hace 40 años y, en consecuencia, el VaR se ha vuelto popular entre otras empresas comerciales, incluso los reguladores financieros han prestado atención al modelo (Linsmeier, TJ y Pearson, ND). 2000). Por ejemplo, la Comisión de Bolsa y Valores de los Estados Unidos inscribió el VaR en una lista de métodos cuantitativos para calcular el riesgo de mercado y la propiedad en 1997 (ibid).

En realidad, según los artículos de Lechner, LA y Ovaert, TC (2010), así como Linsmeier, TJ y Pearson, ND (2000), VaR es una ecuación de estimación expresada en unidades monetarias que no exceden la pérdida en el rango de magnitud durante un período de tiempo y nivel de confianza dados. Típicamente, el nivel de confianza de la estimación del modelo (99%, 97.5%, 95%) o, en otras palabras, la probabilidad de que ocurra algún caso desfavorable y la influencia en el mercado son iguales a 1, 2.5 y 5 por ciento (ibid).

Se puede describir la conocida ecuación del VaR (Phelps S, 2018):

$$$(1) \ VaR (X) = \ min \ \ {x \ \ epsilon \ R: 1-F_x (-x) \ geq \ alpha \}$

Donde X es una variable aleatoria que realiza la cantidad del valor de la cartera y es una función de distribución acumulativa (ibid).

Por otro lado, Hooper GP (1996, citado en Lechner, LA y Ovaert, TC 2010) denota VaR con confianza alfa define de una manera bastante elemental:

$$$(2) \ VaR ^ \ alpha (X) = \ sigma \ sqrt {\ delta t} N ^ {- 1} \ alpha$

Donde $$$\ sigma$es la desviación estándar de las devoluciones de acciones seleccionadas, $$$\ delta t$es la raíz cuadrada del período de tiempo fijo y $$$N ^ {- 1}$es la función de distribución acumulativa (CDF) para una distribución normal (Lechner, LA y Ovaert, TC 2010).

Aunque VaR es un método conocido y manejado para estimar el riesgo de cartera decidido, existen deficiencias en un caso al medir la vulnerabilidad a los problemas finales del mercado, a saber, el ejemplo está relacionado con la probabilidad de que eventos extremos del mercado no se vean adecuadamente atrapados en la cola de la distribución normal (Capiński, MJ 2015). Para resolver este problema, se creó el Valor condicional en riesgo (CVaR) que considera el valor esperado de la pérdida en lugar de VaR (ibid). CVaR se define como:

$$$(3) \ CVaR ^ \ alpha (X) = \ frac {1} {\ alpha} \ int ^ \ alpha_0 VaR ^ \ beta (X) d \ beta = \ frac {-1} {\ alpha} q ^ \ beta (X) d \ beta$

$$$(4) \ CVaR ^ \ alpha (X) = - \ frac {1} {\ alpha} (E [X 1 _ {\ {X \ leq q ^ \ alpha (x) \}}] + q ^ \ alpha (X) (\ alpha-P [X \ leq q ^ \ alpha (X)]))$

Donde Ahn D.-H. et.al (1999, citado en Capiński, MJ 2015) interpretan $$$-q ^ \ alpha (X)$
como VaR de X variable aleatoria (retorno del precio de una acción) con probabilidad $$$\ alpha$y se define como el cuantil superior de X.

Además, Acerbi C. y Tasche D. (2002, citado en Capiński, MJ 2015) confirman: "El CVaR es una medida de riesgo coherente". Rockafellar, RT y Uryasev, S. (2000) observan que CVaR tiene características adicionales: equivalentes de transición, positivamente homogéneos, convexos, etc.

El siguiente capítulo del artículo demuestra la implementación del bien conocido Valor en riesgo (VaR) y Valor condicional en riesgo (CVaR) también anunciado como Déficit esperado (ES) notado en el trabajo de Rockafellar, RT y Uryasev, S. (2000) mediante el uso de tecnología de la información en datos reales.

Metodología

Consideremos los métodos más utilizados para calcular VaR, así como sus ventajas y desventajas.

Según el informe de Lechner, LA y Ovaert, TC (2010), la simulación histórica es un enfoque generalizado para evaluar VaR y su modificación. En el modelado histórico de los datos, tomamos los valores de las fluctuaciones financieras de la cartera que ya se conocen de mediciones pasadas. Por lo tanto, es solo una secuencia lógica que la desventaja de este método es la imposibilidad de construir predicciones para carteras sin una pieza de información al respecto. El método de Monte Carlo es idéntico en muchos aspectos al método de modelado histórico, que se utiliza para una técnica de alta precisión, la principal diferencia clara de que el cálculo de la simulación de Monte Carlo no se basa en datos reales, sino que se realiza en valores generados aleatoriamente. La ventaja de este método es la posibilidad de considerar como un gran número de situaciones, y emular el comportamiento del mercado en condiciones extremas, así como no es necesario una aproximación entre los factores de riesgo y los cambios en una cartera (Glasserman, P., Heidelberger, P y Shahabuddin, P., 2002). El inconveniente obvio son los grandes recursos computacionales necesarios para implementar este enfoque (ibid).

Naturalmente, estos no son los únicos métodos para calcular los modelos VaR. Además, existen modelos lineales y cuadráticos simples de predicción de precios, y un método de variaciones bastante complicado, que no se trataron en el ensayo.

Análisis de datos

Como datos secundarios para probar la evaluación precisa, se toma el stock de KAZ Minerals. Para aclarar el trabajo, el precio cerrado ajustado se toma para simulación en un modelo. Las acciones de la empresa KAZ Minerals (KAZ.L) es uno de los valores que negocian con éxito entre las empresas kazajas en la Bolsa de Londres (LSE), y se clasifica en la lista de Compañías Comerciales Premium Equity (Bolsa de Londres, 2019). La entidad se presenta como la compañía minera de cobre masiva en Kazajstán (Kazminerals.com. 2019).

Los datos históricos del precio de la acción se descargan del sitio web de Yahoo Finance (Finance.yahoo.com, 2019). Para garantizar la validez del trabajo, se observa el período de un año desde el 22 de marzo de 2018 hasta el 22 de marzo de 2019. Además, para evitar la interrupción de la información, en el análisis, los datos históricos del precio de la acción KAZ.L se descargan en formato de valores separados por comas (CSV) debido a que el formato CSV es compatible con el programa Microsoft Excel (Excel) . Los datos elegidos del proyecto se presentan como un gráfico lineal utilizando Excel en la Figura 1.

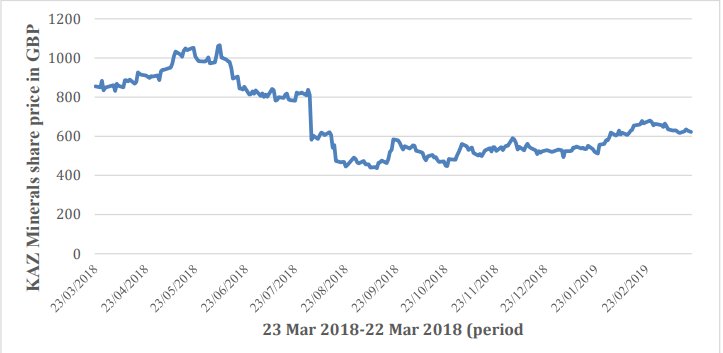
Figura 1. La dinámica del cambio Precio de las acciones de KAZ Minerals por un año

Debido a la limitación de la línea de tiempo del informe, en lugar de utilizar un lenguaje de programación como Python para la implementación de modelos de evaluación, los datos se analizan completamente en Excel.

Hallazgos

En la sección anterior, los modelos para pronosticar las pérdidas potenciales en una cartera basada en la ecuación VaR y CVaR y los cambios utilizados en el precio de las acciones de KAZ Minerals del 23 de marzo de 2018 al 23 de marzo de 2019, descargados de la fuente web oficial Yahoo Finance (Finance.yahoo. com, 2019). Ambas ecuaciones ejecutadas para cada fecha del período elegido.

La Tabla 1 muestra el rendimiento medio diario de la empresa, una desviación estándar de los rendimientos, un valor mínimo de los rendimientos y un valor máximo de los rendimientos para este ejemplo.

Tabla 1. Rendimiento medio compartido y desviación estándar de los retornos

La media correspondiente es -0.0006 y la desviación estándar 0.0355 de los retornos para los KAZ Minerals de seguridad únicos seleccionados. Además, la varianza de los retornos es 0.0013. Además, eso ciertamente debe subrayarse que en el trabajo de investigación de Vee, DNC y Gonpot, P. N (2014), los rendimientos de las acciones de Kazajstán mostraron un valor significativo en la volatilidad, sin embargo, la estimación se relacionó con el índice de la Bolsa de Kazajstán en pre y después del período 2008. Además, debe mencionarse que el valor máximo entre los retornos es 0.0998, así como el valor mínimo entre los retornos es -0.2829 en la distribución de pérdidas. La Tabla 2 presenta los valores máximos y mínimos entre el precio ajustado de las acciones cercanas (KAZ.L) en la negociación de la libra esterlina (GBP) en la Bolsa de Londres del 23 de marzo de 2018 al 22 de marzo de 2019.

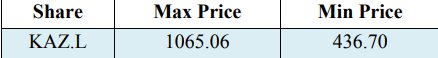
Tabla 2. El precio máximo y mínimo de las acciones de KAZ Minerals en GBP

El siguiente paso es la evaluación de Valor en riesgo (VaR) y Valor condicional en riesgo (CVaR) para el nivel de confianza: 0.99, 0.972 y 0.95. Los valores se revelan en la Tabla 3.

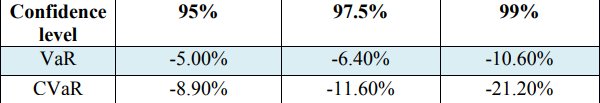
Tabla 3. Valores de VaR y CVaR de los retornos

El tamaño de la muestra de la simulación se toma 252 unidades del 23 de marzo de 2018 al 22 de marzo de 2019 durante un año.

Discusión

En el informe, las ecuaciones VaR y CVaR demuestran el valor creíble en el caso de los modelos de estimación para el precio de una acción de la compañía kazaja en el período de corto plazo. Con estos valores por un lado, ambos métodos presentan resultados adecuados para evaluar el valor de las amenazas para la cartera de inversiones (Linsmeier, TJ y Pearson, ND 2000; Lechner, LA y Ovaert, TC 2010).

Además, según los hallazgos de la Tabla 2, el siguiente aviso es sencillo de que los valores de CVaR son más masivos en comparación con los valores de VaR en todas las medidas de nivel de confianza. Se le puede dar una explicación por el hecho de que el CVaR toma el riesgo promedio de la cartera elegido, por lo tanto, es más sensible en la cola de la distribución de pérdidas que el VaR. Esto prueba una vez más que CVaR es un riesgo coherente (Acerbi C. y Tasche D., 2002, citado en Capiński, MJ 2015; Rockafellar, RT y Uryasev, S. 2000). Por ejemplo, con respecto a la adecuación de ambos modelos de estimación, con un nivel de confianza de 99% VaR y CVaR ilustra el porcentaje significativo de pérdida por rendimiento de las acciones. Para ser precisos, podría detectarse que VaR es -10.60% y CVaR es -21.20%. Está bastante claro la razón de las medidas colosales de CVaR con un nivel de confianza dado del 99% debido al hecho de que el rango de precio de las acciones durante el período, el precio máximo es 1065.06 GBP, el precio mínimo de las acciones es 436.70 GBP, respectivamente.

Conclusión

Habiendo considerado todo lo anterior, obviamente debería mencionarse nuevamente que el objetivo del informe es demostrar la estimación del valor de la posible pérdida para la compañía kazaja (KAZ Minerals) durante un período del 23 de marzo de 2018 al 22 de marzo de 2019. formado en las ecuaciones de Valor en riesgo (VaR) y Valor condicional en riesgo (CVaR). Las actuaciones de la simulación se comparan entre sí en el mismo período de tiempo. Los resultados muestran el valor significativo para cada método y prueban el trabajo previo en el mismo área que CVaR tiene medidas más precisas en comparación con VaR (Acerbi C. y Tasche D., 2002, citado en Capiński, MJ 2015; Rockafellar, RT, y Uryasev, S.2000).

A pesar de las críticas, VaR es una herramienta generalizada en todas las instituciones financieras hasta la actualidad y existe una amplia gama de su versión de modificación. Debido a los obstáculos del complejo cálculo en la investigación profunda, el experimento se realiza utilizando Microsoft Excel en lugar de utilizar un lenguaje de programación como Python, y los resultados se revelan en el informe. Los resultados del ensayo pueden servir de base para seguir trabajando en el uso de medidas de evaluación de riesgo complejas para la cartera en la industria bursátil, la industria de seguros y la industria de inversión.