Sobre la aplicación de la teoría de los procesos ARMA en la práctica de la ingeniería.

A continuación, diremos algunas palabras sobre la alternativa de tiempo discreto a los modelos matemáticos en forma de ecuaciones diferenciales lineales que generalmente se conocen, pero a menudo bastante inesperadas para los ingenieros, a saber, modelos autorregresivos: promedio móvil y perspectivas muy inusuales para tal modelado, cuyas capacidades exceden significativamente lo que está acostumbrado a obtener de LDU.

La lista de capacidades potenciales de la tecnología incluye el análisis de sistemas con una perturbación entrante inaccesible para la observación, la determinación de las propiedades de resonancia de dichos sistemas, el espectro y el proceso de excitación externa, la estimación espectral de los procesos por sus cortas realizaciones, el modelado del comportamiento de los sistemas a baja frecuencia de muestreo a lo largo del tiempo, etc.





Los procesos ARMA, bien conocidos por los economistas (más precisamente, "economometristas"), son mucho menos conocidos por los especialistas en regulación automática y, en mi opinión, apenas son utilizados por ingenieros mecánicos e ingenieros de radioelectrónica, especialmente los de la "vieja escuela". El artículo intenta indicar algunas áreas posibles de aplicación de la teoría ARMA en la práctica de la ingeniería.
En pocas palabras, simplificado, para aquellos que no están familiarizados con el tema, sobre el cual, de hecho, lo es. El proceso estocástico de tiempo continuo x (t) por razones obvias "digitales" en la práctica generalmente coincide con la secuencia de tiempo discreto x [i] con el intervalo de muestreo Δt.
En principio, para cualquier proceso x [i] es posible una representación de la forma

x [i] - a ₁ · x [i-1] - a ₂ · x [i-2] - ... - a _p · x [ip] = b ₀ · f [i] + b ₁ · f [i- 1] + ... + b _q · f [iq] (1),

donde a _k y b _k son coeficientes constantes (para este modelo), llamado modelo de promedio móvil de autorregresión con el orden de autorregresión p y el promedio móvil q. o un modelo ARMA (p, q), f [i] es una especie de proceso "entrante", sobre el cual es un poco más bajo. A menudo (1) se escribe en una forma ligeramente diferente (6).
Básicamente, es solo un filtro digital que tiene partes recursivas AR y no recursivas MA.
Existe una correspondencia entre los modelos ARMA (p, q) y los sistemas lineales (por ejemplo, mecánicos), por ejemplo, descritos por la conocida ecuación diferencial lineal de la forma


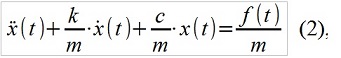
donde m, c, k es la masa, la rigidez y la amortiguación del sistema mecánico, f (t) es la fuerza externa. La contraparte de ARMA se ve así:

x [i] - a ₁ · x [i-1] - a ₂ · x [i-2] = b ₁ · f [i-1] (3),

los coeficientes del modelo se pueden encontrar fácilmente a través de los valores propios λ ₁ y λ ₁ * (por brevedad, se considera el caso "oscilante") del sistema lineal y Δt:

a ₁ = z + z *, a ₂ = - z · z *, b ₁ = j (z * -z) · Δt / (2mω ₁ ),

donde z = exp (λ ₁ · Δt), λ ₁ = -ε ₁ + jω ₁ , j es la unidad imaginaria, * es la conjugación compleja

para referencia:

Para el sistema de prueba, m = 1 kg, c = 100 N / m, k = 0.75 kg / s, Δt = 0.12 s.,
modelo ARMA (2,1) obtenido

x [i] - 0.69433x [i-1] +0.91393 x [i-2] = 0.010696f [i-1]

(Una explicación muy breve de cómo (3) se obtiene generalmente de (2). La función de transición de pulso de nuestro sistema lineal, es decir, la respuesta del sistema a un solo pulso:



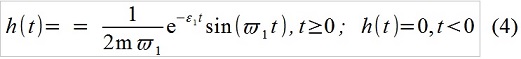
El registro (2) en la forma "integral" se denomina "convolución" f (t) y h (t), lo que significa que implica considerar la acción externa como una secuencia de impulsos elementales. En tiempo discreto, escriba, bueno, por ejemplo, así:



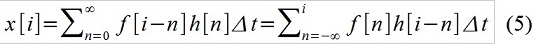
Al agregar x [i], x [i-1] yx [i-2] usando los factores seleccionados 1, a ₁ y a _2, logran la aniquilación mutua de las "colas" infinitas h [i] - f [i] permanece en el lado derecho · H [0] = f [i] · 0 yf [i-1] · h [1] = f [i-1] · b ₁ . Desde el punto de vista de la teoría ARMA, el modelo de dimensión infinita del promedio móvil MA (∞) se transforma en ARMA (2,1) (aunque algunos dirán que se obtuvo por accidente un modelo puramente autorregresivo AR (2) = ARMA (2,0).

Observación 1. Un lector que esté familiarizado con el procesamiento digital de procesos dirá que simplemente discretizar h (t) no es muy correcto: es necesario limitar la función h (t) por frecuencia a 1 / (2Δt) (filtro). De lo contrario, hay un error de enmascaramiento de frecuencia. Los gráficos de la respuesta de frecuencia y la respuesta de fase de nuestro sistema, los modelos "analítico" y ARMA, muestran por qué este error en la mayoría de los casos de ingeniería puede ser descuidado (Fig. 1) (aquí, la respuesta de frecuencia está en una escala logarítmica).

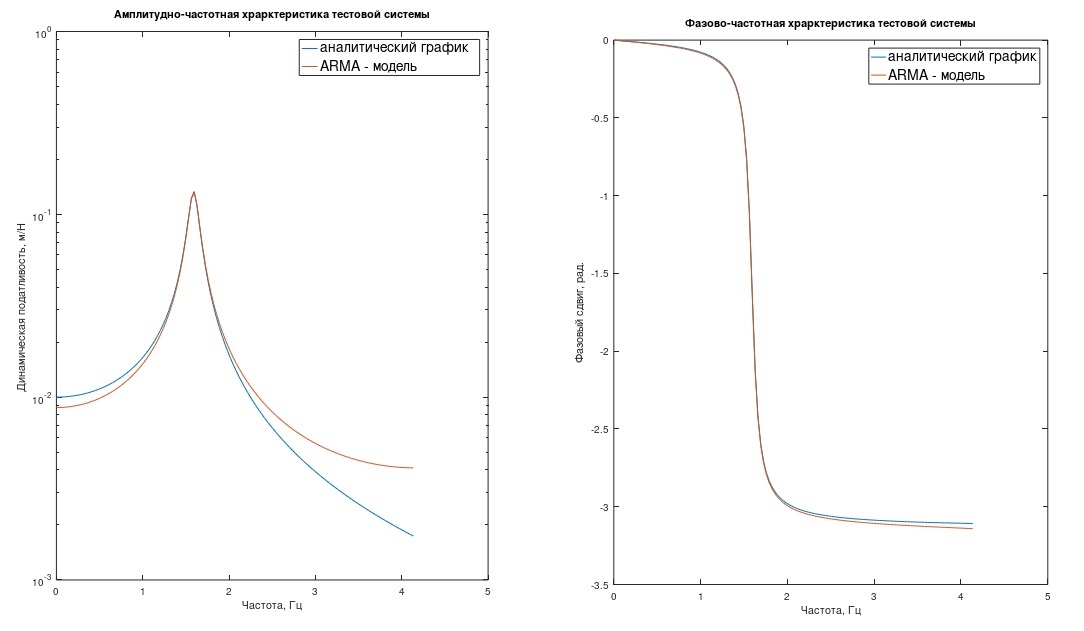
Fig. 1 Respuesta de frecuencia y respuesta de fase del sistema de prueba.

Observación 2. En la práctica, el orden del modelo ARMA puede ser significativamente mayor que el ejemplo considerado anteriormente, debido, por ejemplo, a varios grados de libertad de un sistema mecánico o un espectro complejo de influencia externa real.

Observación 3. Muy importante. Existen métodos (no considerados aquí; se pueden escribir muchos más artículos sobre ellos) que permiten estimar los parámetros del modelo ARMA (es decir, el orden del modelo p y q y los coeficientes a _k y b _k ) solo por el proceso resultante x [i], bajo el supuesto que f [i] es un ruido blanco hipotético cuya varianza también se puede estimar. En general, dicha evaluación es la parte principal de toda la teoría ARMA. Si bien estos métodos no difieren en la perfección particular, son de considerable interés.

Ahora sobre por qué, de hecho, todo esto puede (o podría) aplicarse en la práctica. Además de lo bastante obvio: la construcción rápida de sinusoides amortiguadas (y no amortiguadas) "manualmente" a partir de los primeros dos puntos y dos coeficientes a ₁ y a ₂ , hay, en mi opinión, aplicaciones más serias de estos modelos en la práctica de la ingeniería.

1. Bueno, en realidad, para la simulación de la operación del sistema: damos una señal externa real f [i] a la entrada, obtenemos x [i] en la salida:

x [i] = a ₁ · x [i-1] + a ₂ · x [i-2] + ... + a _p · x [ip] + b ₀ · f [i] + b ₁ · f [i- 1] + ... + b _q · f [iq] (6)

El modelo ARMA hace frente a la tarea mejor que el modelo de diferencia finita, sin embargo, esto se nota solo en grandes intervalos de muestreo Δt. (en la Fig. 2, Δt = 0.12 s (izquierda) y 0.03 s). En qué casos tiene sentido meterse con ARMA, usted decide.

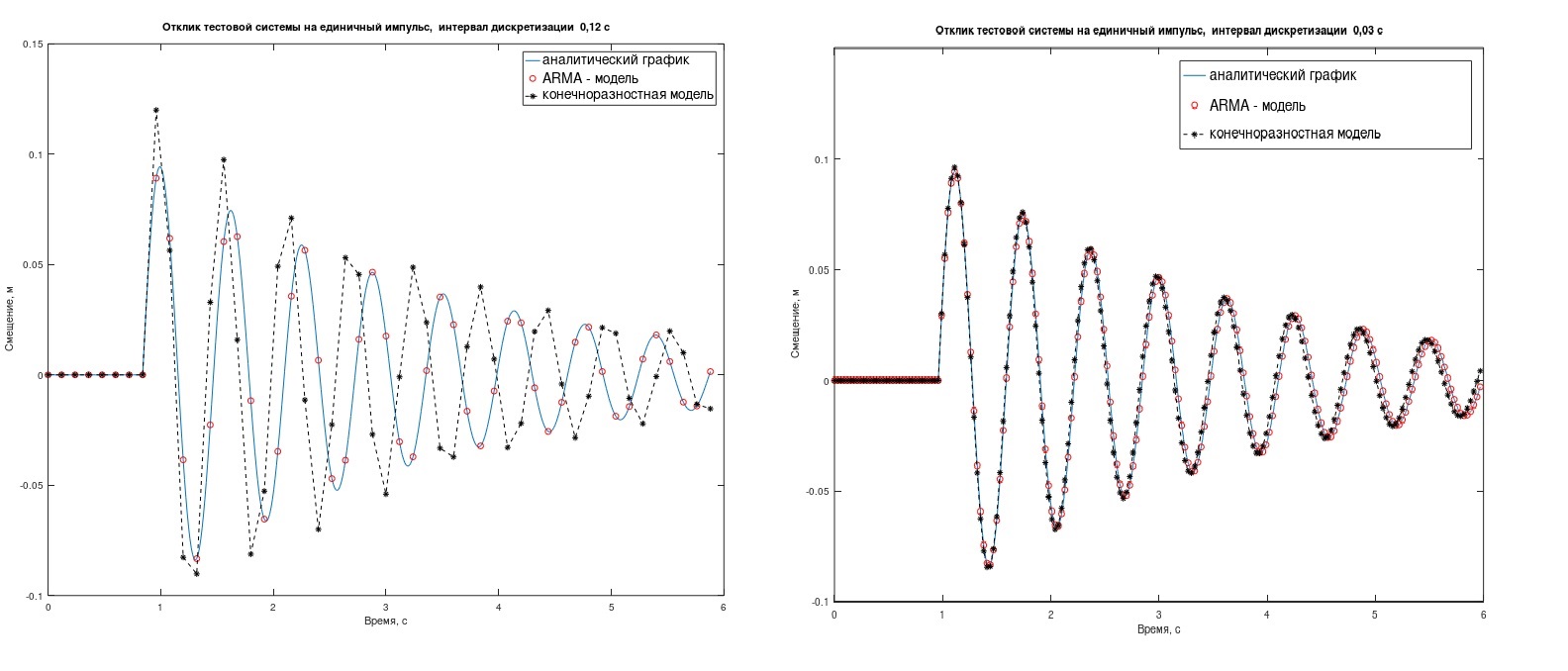
fig. 2. La respuesta de los sistemas de prueba a un solo impulso.

2. Para la estimación espectral, especialmente cuando la longitud de implementación del proceso estacionario es insuficiente para la observación. Quizás esta sea la aplicación de ingeniería más famosa de los modelos ARMA. Dado que se obtendrá un cierto filtro digital y la variación del ruido blanco que ingresa para el proceso en estudio, la tarea de construir una estimación del PSD se resuelve de una manera obvia. De hecho, es posible obtener gráficas SPM externamente muy "suaves" y al mismo tiempo crear la impresión de alta resolución. La mejora esperada en la evaluación está asociada con el hecho de que el investigador aporta información externa sobre la naturaleza del proceso a la construcción de la evaluación, generalmente estableciendo un orden de modelo conocido.
En resumen, debe saber qué tan aproximado debería ser este PSD. Los estudios "exploratorios" de esta implementación que utilizan métodos clásicos pueden hacer poco, principalmente en referencia a estudios clásicos (basados ​​en FFT) de naturaleza similar, pero realizaciones significativamente más largas. Existe la posibilidad de errores graves.

3. Para el análisis de las propiedades de resonancia del sistema y el espectro de la acción externa, en el caso de que el verdadero efecto externo no esté disponible para observación. Como ya se señaló, es posible, conociendo el proceso x [i], determinar todos los coeficientes del modelo a _k y b _k (y la varianza del ruido blanco entrante). Utilizándolos, determinando las raíces de dos polinomios con los coeficientes correspondientes, es fácil encontrar p "polos" y q "ceros" del modelo (λ _k y μ _k ) y construir su función de transferencia; probablemente ni siquiera pueda usar la forma ARMA (aquí dado), y en la forma habitual "analítica", como descubrimos anteriormente (Fig. 1), la diferencia es pequeña. Por ejemplo, para p = 5, q = 3 (al abstraerse de las restricciones existentes, aparentemente, en la relación de pyq), como una opción, tenemos:



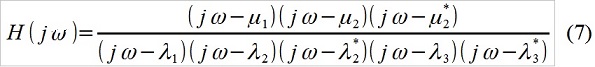
Todo está muy, muy simplificado, por supuesto. Basado en la naturaleza conocida del objeto en estudio (por ejemplo, estas son pruebas de polígono de la suavidad de manejo del automóvil) y el impacto externo (microperfil de la carretera), el investigador decidió reescribir la función de transferencia, por ejemplo:




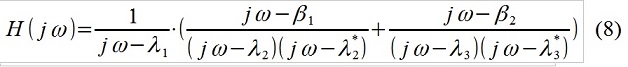
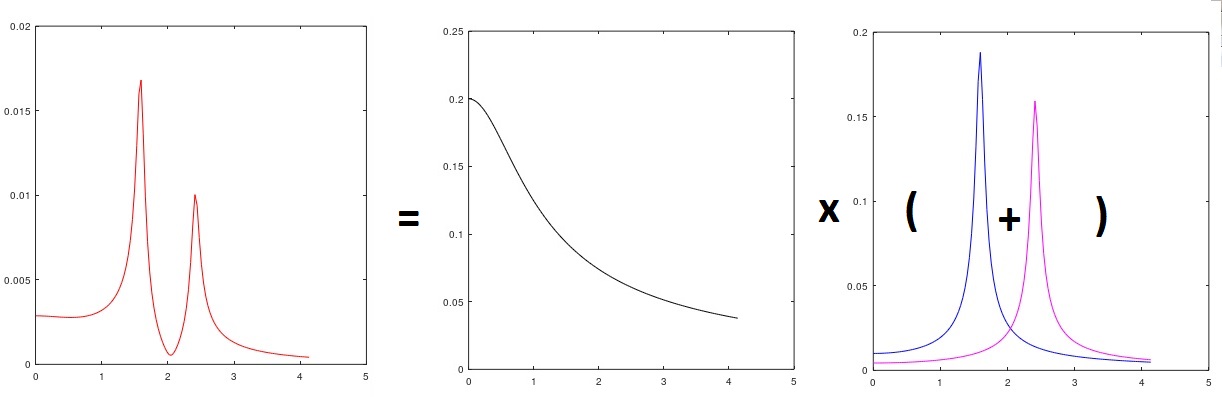
Fig. 3 Análisis del espectro de señal con la asignación de la perturbación entrante

y comentó: la parte del modelo asociada con λ ₁ es obviamente (hasta cuadrar y multiplicar por la varianza del ruido blanco hipotético entrante) el microperfil "rosado" de la carretera (Fig. 3) (es decir, identificamos un espectro desconocido de real la señal de entrada, seleccionada manualmente, parece ser "similar"), λ ₂ y λ ₃ son las propiedades resonantes del cuerpo en la suspensión (posiblemente modos de vibración longitudinal-angular y vertical). El principal problema será, por supuesto, determinar los parámetros del modelo ARMA. Para los recién descritos, a veces, sin ningún ARMA, puede "gatear" a la antigua usanza (aunque sea en forma electrónica) de acuerdo con el gráfico de densidad espectral y medir anchos de pico a un nivel de -3 dB, etc., o aplicar curvatura, a veces incluso con gran éxito .

3. Para predicción lineal x [i]. Aparentemente, la aplicación principal de ARMA es para economistas. Se puede ver a partir de (6) que si los coeficientes del modelo se estimaron utilizando los métodos descritos anteriormente, el siguiente valor x [i] se puede estimar exacto a un hipotético ruido blanco inaccesible para la observación b ₀ · f [i], la varianza de este ruido blanco se estima junto con los coeficientes del modelo. Por lo general, en este caso, está implícito el ajuste dinámico (en tiempo real) de los parámetros del modelo. Aparentemente, puede ser útil en sistemas de vibración activa y reducción de ruido. Los especialistas en TAP lo saben mejor.

4. Para restaurar un proceso inaccesible que no se puede observar. Al dividir el modelo en partes, como se muestra arriba en la Sección 3, basado en el conocimiento sobre la naturaleza del proceso en estudio, es posible evaluar por separado el espectro de la perturbación entrante, y por separado, las propiedades oscilatorias del sistema físico (separe el modelo en partes). Puede ir más allá: cree un filtro (modelo ARMA, el inverso del modelo original) que conecte la salida del sistema con la entrada, y con su ayuda del proceso resultante x [i] obtenga una implementación temporal de la perturbación entrante. Por ejemplo, intente restaurar una señal no distorsionada grabada con distorsiones lineales desconocidas con precisión por un equipo que no está disponible para un estudio separado (por ejemplo, obtenido por telemetría).

Basado en mi humilde conocimiento, como resultado expresaré un juicio tan subjetivo. La aplicabilidad de las tecnologías ARMA a los problemas de ingeniería depende en gran medida de la perfección de los métodos para estimar los parámetros de estos modelos a partir de la señal resultante, o más bien, en mi opinión, está fuertemente limitada por la imperfección de estos métodos. La acumulación de experiencia en la aplicación de ARMA en ingeniería parece tener sentido, principalmente, en previsión de un "avance" muy probable en esta área.