Prólogo

Creo que debemos explicar brevemente por qué de repente un tema aparentemente tan trivial con el cálculo del presupuesto de energía y por qué exactamente los satélites CubeSat. Bueno, aquí todo es bastante simple: mi breve práctica docente demostró (para mí) que este tema, aunque básico, estaba lejos de ser entendido por todos la primera vez y, además, tenía varias preguntas que no eran obvias en la primera lectura. Además, parece que en cosas tan básicas todavía publican artículos en IEEE y esto está lejos de ser hecho por los estudiantes . ¿Por qué exactamente CubeSat? Todavía es más simple aquí: el formato satelital es interesante (el hecho de la existencia de micro y nano-satélites, como resultó, sumerge a muchos en un estado de shock corto), y por lo tanto es muy adecuado para fines educativos.

La simulación se llevará a cabo en Python 3 por las mismas razones que expresé en mi publicación anterior . Consideraremos el caso de órbita baja (LEO - órbita terrestre baja) y calcularemos, de hecho, la relación señal-ruido (SNR - relación señal-ruido) en la entrada del receptor a través de un enlace descendente (DL - enlace descendente). Usaremos varios directorios de acceso abierto y crearemos gráficos para mayor claridad.

Todos los códigos fuente están disponibles en mi repositorio de GitHub , ¡invito a todos los interesados a leerlo! ¡Estaré muy agradecido por la revisión del código y la crítica constructiva!

Vamos!

¿Qué fórmulas calcularemos?

En primer lugar, por supuesto, esta es una fórmula bien conocida para la relación señal-ruido en una escala logarítmica (en decibelios, simplemente) para todos (involucrados en el tema), donde tenemos en cuenta todas las posibles pérdidas y amplificaciones con una cierta cantidad de abstracción:

$SNR = P_t + G_t + G_r + \ eta_ {t} + \ eta_ {r} - L_r - L_t - L - L_ {add} - N [dB] \ qquad (1)$

donde - potencia total del ruido térmico (tiene una relación conocida con la densidad espectral del ruido $N_0 = kT_ {ruido}$ ) en dBm (decibelios por milivatio), P_t - potencia transmitida en dBm, G_t y G_r - ganancia de antena en el lado del transmisor y el receptor, respectivamente (en dBi - decibelios isotrópicos), $\ eta_ {t}$ y $\ eta_ {r}$ - ganancia del alimentador del transmisor y receptor (en dB), L_t y L_r - pérdidas en alimentadores (en dB), pérdidas en el camino de propagación de la onda electromagnética en dB, $L_ {add}$ - pérdidas adicionales (por así decirlo, cierto margen) en dB.

En general, con los primeros siete términos es más o menos claro: estos son datos de referencia. Las cosas son más interesantes con los últimos tres participantes en el proceso.

Potencia de ruido térmico

Como sabes, no hay ningún lugar para esconderse de este flagelo de dispositivos electrónicos, solo puedes tener en cuenta:

$N = 10lg \ left (\ frac {kT_ {noise} B_ {noise}} {10 ^ {- 3}} \ right) [dBm] \ qquad (2)$

donde - constante de Boltzmann $T_ {ruido} = T_a + T_e$ - temperatura de ruido equivalente, T_a - la suma de las pérdidas de la antena y el ruido (fondo) del cielo, $T_e = T_0 (F_ {sys} -1)$ - temperatura de ruido del receptor ( T_0 = 290K y $F_ {sys} = 10 ^ {\ frac {NF} {10}}$ - figura de ruido, que puede estimarse a partir de la imagen de ruido ( - figura de ruido) de la antena receptora), y $B_ {ruido}$ - el ancho de la banda de frecuencia de ruido. Puede tomar la banda de ruido igual al ancho de banda del receptor sin embargo, de acuerdo con [1, p. 98] el ancho de banda de ruido $B_ {ruido}$ se puede calificar un poco más exactamente como $\ gamma B$ donde $\ gamma$ - constante de 1.002 a 1.57 (se refiere a la configuración del receptor).

Pérdidas adicionales

Aquí puede tomar algún tipo de suministro garantizado, recogido, como regla, de los mismos directorios, o profundizar y calcular todo usted mismo.

En esta sección, me baso casi por completo en el viejo libro de texto de Cantor, a saber, esta parte del mismo [1, p. 88-96]. Si los lectores tienen fuentes autorizadas más relevantes, por favor comparta, creo que será útil para todos.

A lo que principalmente prestamos atención:

Pérdida debida a la refracción e imprecisión del puntero de la antena ( Pérdida de haz de antena )

Son designados como $L_b = 10log_ {10} (1+ (2 \ theta / \ theta_ {0.5}) ^ 2)$ donde $\ theta$ - ancho de haz y $\ theta_ {0.5}$ - el ancho del haz de media potencia, y depende, sin importar cuán difícil de adivinar, de las características de ciertos dispositivos de antena:

Efectos de fase atmosférica

Si cree en los clásicos, estas pérdidas afectan principalmente la velocidad de transferencia de datos debido al ancho de banda del receptor, porque es aconsejable elegir la banda de acuerdo con la tabla 1 [1, p. 91]. Para evitar la distorsión de fase.

Tab. 1. Ancho de banda máximo del receptor para diferentes rangos.

Frecuencia portadora, GHz	0.5 0.5	1	5 5	10
Ancho de banda del receptor (B), MHz	10	25	270	750

Sin embargo, debe tenerse en cuenta que las cifras son muy impresionantes y, a menudo, no se consideran, más bien, debido al ruido térmico.

Pérdida debido a la falta de coincidencia de polarización de la antena

Se puede estimar en función de los coeficientes de elipticidad. $e_1$ y $e_2$ (Adjunto un recorte del libro soviético como Figura 1).

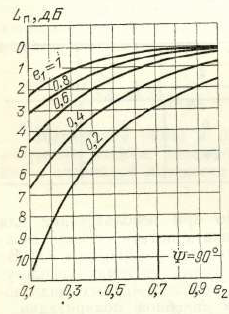
Fig.1. Dependencia de las pérdidas debido a la falta de coincidencia de polarización entre las antenas de transmisión y recepción en la elipticidad. [1, p. 93]

Sin embargo, me encontré con este parámetro como referencia. Por ejemplo, al calcular el presupuesto de energía para el NanoCom AX100, la pérdida de polarización es de 3 dB (la pérdida atmosférica es de 2.1 dB, la pérdida ionosférica es de 0.4 dB).

Atenuación atmosférica

Podemos evaluar este parámetro interesante de acuerdo con las recomendaciones de la UIT , o calcularlo nosotros mismos. Afortunadamente, hay bibliotecas especiales como esta .

Atenuación a lo largo del camino de propagación de ondas electromagnéticas (pérdida de camino)

Sin más preámbulos, aplicamos la fórmula de Friis para comenzar con :

$L = 20lg \ frac {\ lambda} {4 \ pi d} [dB] \ qquad (3)$

donde $\ lambda$ - longitud de onda electromagnética (se relaciona de manera conocida con la frecuencia portadora $f_0 = \ frac {c} {\ lambda}$ , Es la velocidad de la onda electromagnética (la velocidad de la luz, si es más simple), y - la distancia entre los satélites y la estación terrestre.

Y aquí llegamos, quizás, a la pregunta más interesante: ¿qué distancia debemos tomar para los cálculos? Como ya se mencionó en la introducción, estamos considerando los satélites LEO, lo que significa que nuestro supuesto satélite se está moviendo en relación con la Tierra (en contraste con el caso geoestacionario, en el que el satélite, por así decirlo, cuelga sobre un punto).

Puede, por supuesto, simplificar todo lo más posible tomando el esquema como base (Fig. 2), cuando se supone que la órbita del satélite de comunicación se encuentra, más o menos, "por encima de la cabeza" de nuestra estación terrestre.

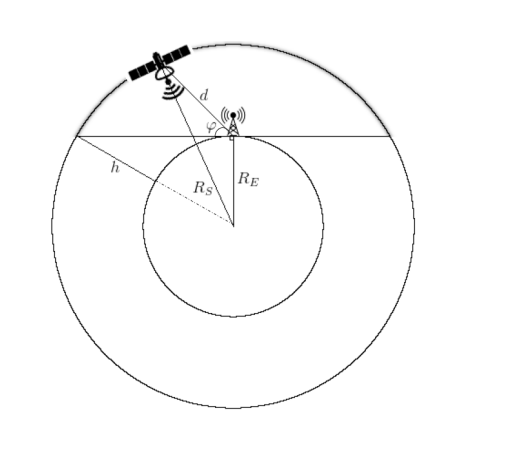
Fig. 2. Descripción esquemática de la trayectoria de CubeSat en órbita terrestre baja [2].

Entonces la distancia puede calcularse mediante la fórmula:

$d = \ sqrt {(R_E + h) ^ 2-R_E ^ 2cos ^ 2 \ phi} - R_Esin \ phi \ qquad (4)$

donde R_E - existe, de hecho, el radio de la Tierra, - altura de la órbita del satélite, y $\ phi$ - ángulo de elevación.

Sin embargo, puede acelerar un poco más, volver al clásico (ya diferente) [3, p.110-123] y calcular todo lo relativo a las coordenadas geográficas reales de la estación terrestre (
$lat_ {gs}$ y $long_ {gs}$ ) y la posición real del satélite (nodo ascendente instantáneo - $L_ {nodo}$ y polo orbital - polo orbital instantáneo ) Prepárese, habrá mucha trigonometría:

$d_ {min} = R_E \ frac {\ sin \ lambda_ {min}} {\ sin \ eta_ {min}} \ qquad (5)$

donde $\ sin \ lambda_ {min} = \ sin (90 ^ 0 - i) \ sin (lat_ {gs}) + \ cos (90 ^ 0 - i) \ cos (lat_ {gs}) \ cos (long_ {gs} - (L_ {nodo} - 90 ^ 0))$ - ángulo central mínimo de la Tierra, $\ eta_ {min} = arctan \ frac {\ sin \ rho \ sin \ lambda_ {min}} {1 - \ sin \ rho \ cos \ lambda_ {min}}$ - ángulo mínimo de nadir, $\ rho = arcsin \ frac {R_E} {R_E + h}$ Es el radio angular de la Tierra. La distancia máxima se puede calcular mediante:

$d_ {max} = R_E \ frac {\ sin \ lambda_ {max}} {\ sin \ eta_ {max}} \ qquad (6)$

donde $\ sin \ eta_ {max} = \ sin \ rho \ cos \ epsilon_ {min}$ y $\ lambda_ {max} = 90 ^ 0 - \ epsilon_ {min} - \ eta_ {max}$ ( $\ epsilon_ {min}$ - ángulo de elevación mínimo del satélite).

Para resumir un breve resumen de los parámetros :

Lo que elegimos como puntos de partida : frecuencia de la portadora, altitud de la órbita (tal vez la posición del satélite y las coordenadas geográficas de la estación terrestre, depende de la precisión que queramos obtener);
Encontramos parámetros ajustables y dependientes del equipo : potencia transmitida, ancho de banda del receptor;
Encontramos datos de referencia : ganancia y pérdida de antena, ganancia y pérdida del alimentador, temperatura de ruido, pérdida adicional.

Simulamos lo que sucedió como resultado

Como fuente de parámetros técnicos para la evaluación del enlace descendente, tenemos disponibles ejemplos reales de transceptores y antenas para satélites CubeSat, como el NanoCom AX100 y el NanoCom ANT430 . Para un ancho de banda mayor, es mejor, por supuesto, considerar la banda S. La antena de parche NanoCom ANT2000 y el transceptor NanoCom SR2000 están disponibles para este rango.

Comenzamos a verificar lo que sucedió.

from SmallSatLB import * import pandas as pd

Toda la lógica se divide condicionalmente en dos opciones: 'borrador' , en el cual la fórmula (4) se usa para calcular la distancia; y 'preciso' , en el que se usan las fórmulas (5) y (6).

'borrador'

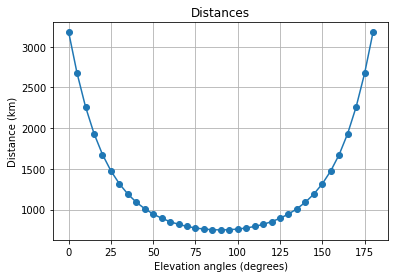
 l_d = LinkBudget(750*1e3, 'draft') #   (   ) d = l_d.distance() #   phi = np.pi*np.array(range(0,181,5))/180 #     plt.plot(180*phi/np.pi, d*1e-3, '-o') plt.title('Distances') plt.xlabel('Elevation angles (degrees)') plt.ylabel('Distance (km)') plt.grid()

 snr, EIRP = l_d.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) #  SNR plt.title('Expected SNRs') plt.xlabel('Elevation angles (degrees)') plt.ylabel('SNR (dB)') plt.legend() plt.grid()

Belleza!

'preciso'

 l_p = LinkBudget(750*1e3, 'precise',\ L_node = 100+90, incl = 90 - 61.5,\ lat_gs = 22, long_gs = 200, eps_min = 5) snr, EIRP = l_p.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) print(min(snr)) print(max(snr))

 >>> 5.556823874020452 >>> 8.667000351847676

En general, aquí: tenemos una pequeña herramienta para "estimaciones" primarias y cálculos de cuánto se debilitará la señal, mientras va del satélite a la Tierra (o viceversa).
¡Gracias a todos por su atención!

Lista de literatura utilizada :

Kantor L. Ya., Askinazi G.B. Comunicaciones por satélite y radiodifusión: un libro de referencia . - Radio y comunicaciones, 1988.
Otilia Popescuy, Jason S. Harrisz y Dimitrie C. Popescuz, Diseño del subsistema de comunicación para misiones de cubos de satélites de nanosaatélites: Perspectivas operativas y de implementación, 2016, IEEE
Wertz JR, Larson WJ Misión espacial Análisis y diseño, Biblioteca de tecnología espacial. - Microcosm Press y Kluwer Academic Publishers, El Segundo, CA, EE. UU., 1999.

Calculamos el presupuesto de energía de una línea de radio para un satélite en formato CubeSat