Termodinámica de agujeros negros.

¡Feliz día de la cosmonáutica! Le entregamos a la imprenta un "Pequeño libro sobre agujeros negros" . Fue en estos días que los astrofísicos mostraron al mundo entero cómo se ven los agujeros negros. ¿Coincidencia? No pensamos;) Espera, pronto aparecerá un libro asombroso, escrito por Stephen Gabser y Frans Pretorius, traducido por el maravilloso astrónomo Pulkovo, también conocido como Astroded Kirill Maslennikov, el legendario Vladimir Surdin hizo edición científica y la Fundación Trayectoria apoyó su publicación.

Extracto "Termodinámica de agujeros negros" debajo del corte.

Hasta ahora, hemos considerado los agujeros negros como objetos astrofísicos que se formaron durante las explosiones de supernovas o se encuentran en los centros de las galaxias. Los observamos indirectamente, midiendo las aceleraciones de estrellas cercanas a ellos. El famoso registro de ondas gravitacionales por el receptor LIGO el 14 de septiembre de 2015 se convirtió en un ejemplo de observaciones más directas de colisiones de agujeros negros. Las herramientas matemáticas que utilizamos para comprender mejor la naturaleza de los agujeros negros son: geometría diferencial, ecuaciones de Einstein y poderosos métodos analíticos y numéricos utilizados para resolver las ecuaciones de Einstein y para describir la geometría del espacio-tiempo que generan los agujeros negros. Y tan pronto como podamos dar una descripción cuantitativa completa del espacio-tiempo generado por el agujero negro, desde el punto de vista astrofísico, el tema de los agujeros negros puede considerarse cerrado. En una perspectiva teórica más amplia, todavía hay muchas oportunidades para la investigación. El propósito de este capítulo es hablar sobre algunos logros teóricos de la física moderna del agujero negro, en el que las ideas de termodinámica y teoría cuántica se combinan con la teoría general de la relatividad, dando lugar a nuevos conceptos inesperados. La idea básica es que los agujeros negros no son solo objetos geométricos. Tienen temperatura, tienen una entropía enorme y pueden exhibir manifestaciones de enredo cuántico. Nuestra discusión sobre los aspectos termodinámicos y cuánticos de la física de los agujeros negros será más esquemática y superficial que el análisis de las características puramente geométricas del espacio-tiempo en los agujeros negros presentados en capítulos anteriores. Pero estos, y especialmente los aspectos cuánticos, son una parte esencial y vital de los estudios teóricos en curso sobre los agujeros negros, y haremos todo lo posible por transmitir, si no detalles complicados, al menos el espíritu de estos trabajos.

En la teoría general clásica de la relatividad, si hablamos de la geometría diferencial de las soluciones de las ecuaciones de Einstein, los agujeros negros son verdaderamente negros en el sentido de que nada puede salir de ellos. Stephen Hawking demostró que esta situación cambia completamente cuando tenemos en cuenta los efectos cuánticos: los agujeros negros resultan emitir radiación de cierta temperatura, conocida como la temperatura de Hawking. Para los agujeros negros de tamaño astrofísico (es decir, desde agujeros negros de masas estelares hasta supermasivos), la temperatura de Hawking es insignificante en comparación con la temperatura del fondo cósmico de microondas: la radiación que llena todo el Universo, que, por cierto, puede considerarse como una variante de la radiación de Hawking. Los cálculos realizados por Hawking para determinar la temperatura de los agujeros negros son parte de un programa de investigación más amplio en el campo llamado termodinámica de los agujeros negros. Otra parte importante de este programa es el estudio de la entropía de los agujeros negros, que caracteriza la cantidad de información perdida dentro de un agujero negro. Los objetos ordinarios (como una taza de agua, una barra de magnesio puro o una estrella) también tienen entropía, y una de las afirmaciones centrales de la termodinámica de los agujeros negros es que un agujero negro de este tamaño tiene más entropía que cualquier otra forma de materia que pueda acomodarse en Un área del mismo tamaño, pero sin la formación de un agujero negro.

Pero antes de profundizar en una discusión de los problemas asociados con la radiación de Hawking y la entropía de los agujeros negros, hagamos una rápida excursión a los campos de la mecánica cuántica, la termodinámica y el enredo. La mecánica cuántica se desarrolló principalmente en la década de 1920, y su objetivo principal era describir partículas muy pequeñas de materia, como los átomos. El desarrollo de la mecánica cuántica condujo a la erosión de conceptos básicos de física como la posición exacta de una partícula individual: resultó, por ejemplo, que la posición de un electrón cuando se mueve alrededor de un núcleo atómico no puede determinarse con precisión. En cambio, las llamadas órbitas se asignaron a los electrones, en los que sus posiciones reales solo se pueden determinar en un sentido probabilístico. Sin embargo, para nuestros propósitos, es importante no pasar a este lado probabilístico del asunto demasiado rápido. Tome el ejemplo más simple: un átomo de hidrógeno. Puede estar en un cierto estado cuántico. El estado más simple de un átomo de hidrógeno, llamado estado fundamental, es el estado con la energía más baja, y esta energía se conoce con precisión. En un sentido más general, la mecánica cuántica nos permite (en principio) conocer el estado de cualquier sistema cuántico con absoluta precisión.

Las probabilidades surgen cuando hacemos un cierto tipo de preguntas sobre un sistema de mecánica cuántica. Por ejemplo, si se sabe definitivamente que el átomo de hidrógeno está en el estado fundamental, podemos preguntar: "¿Dónde está el electrón?" y de acuerdo con las leyes cuánticas
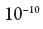
En la mecánica, llegamos a esta pregunta solo una cierta estimación de probabilidad, aproximadamente algo así como: "el electrón probablemente se encuentra a una distancia de hasta medio angstrom del núcleo de un átomo de hidrógeno" metros). Pero tenemos la oportunidad, a través de cierto proceso físico, de encontrar la posición del electrón con mucha más precisión que en un angstrom. Este proceso, que es bastante común en física, consiste en lanzar un fotón con una longitud de onda muy corta en un electrón (o, como dicen los físicos, dispersar un fotón en un electrón), después de eso podemos reconstruir la ubicación del electrón en el momento de la dispersión con una precisión aproximadamente igual a la longitud de onda fotón Pero este proceso cambiará el estado del electrón, de modo que después de eso ya no estará en el estado fundamental del átomo de hidrógeno y no tendrá una energía definida con precisión. Pero durante algún tiempo su posición estará casi exactamente determinada (exacta a la longitud de onda del fotón utilizado para esto). Una evaluación preliminar de la posición del electrón puede llevarse a cabo solo en un sentido probabilístico con una precisión de aproximadamente un angstrom, pero tan pronto como lo medimos, sabemos exactamente a qué era igual. En resumen, si medimos un sistema de mecánica cuántica de alguna manera, entonces, al menos en el sentido generalmente aceptado, "forzosamente" le damos un estado con un cierto valor de la cantidad que estamos midiendo.

La mecánica cuántica es aplicable no solo a los pequeños, sino (como creemos) a todos los sistemas, sino que para los sistemas grandes, las reglas de mecánica cuántica rápidamente se vuelven muy complejas. El concepto clave es el entrelazamiento cuántico, cuyo ejemplo simple es el concepto de giro (rotación). Los electrones individuales tienen un giro, por lo que en la práctica un solo electrón puede tener un giro dirigido hacia arriba o hacia abajo con respecto al eje espacial seleccionado. El giro del electrón es una cantidad observada, porque el electrón genera un campo magnético débil, similar al campo de una barra magnética. Luego, un giro apuntando hacia arriba significa que el polo norte del electrón está apuntando hacia abajo, y un giro apuntando hacia abajo significa que el polo norte está "mirando hacia arriba". Se pueden poner dos electrones en un estado cuántico conjugado, en el que uno de ellos tiene un giro dirigido hacia arriba y el otro hacia abajo, pero es imposible decir cuál de los electrones tiene qué giro. De hecho, en el estado fundamental de un átomo de helio, dos electrones están exactamente en ese estado, llamado spin-singlete, ya que el giro total de ambos electrones es igual a cero. Si separamos estos dos electrones sin cambiar sus espines, podemos continuar afirmando que son espín-singlete juntos, pero aún no podemos decir cuál será el espín de cada uno de ellos individualmente. Ahora, si medimos uno de sus giros y establecemos que está dirigido hacia arriba, entonces estaremos completamente seguros de que el segundo está dirigido hacia abajo. En esta situación, decimos que las espaldas están enredadas; ninguna en sí tiene un significado definido, mientras que juntas están en un estado cuántico definido.

Einstein estaba muy preocupado por el fenómeno del enredo: parecía amenazar los principios básicos de la teoría de la relatividad. Consideremos el caso de dos electrones en un estado spin-singlete, cuando están lejos uno del otro en el espacio. Para mayor claridad, deje que uno de ellos se lleve a Alice y al otro Bob. Supongamos que Alice midió el giro de su electrón y descubrió que estaba hacia arriba, y Bob no midió nada. Hasta que Alice completó su medición, era imposible saber cuál era el giro de su electrón. Pero tan pronto como completó su medición, supo absolutamente que el giro del electrón de Bob se dirige hacia abajo (en la dirección opuesta al giro de su propio electrón). ¿Significa esto que su medición transfirió instantáneamente el electrón de Bob al estado cuando su giro se dirige hacia abajo? ¿Cómo podría suceder esto si los electrones están separados espacialmente? Einstein y sus compañeros de trabajo Nathan Rosen y Boris Podolsky sintieron que la historia de medir sistemas enredados era tan grave que amenazaba la existencia misma de la mecánica cuántica. La paradoja de Einstein - Podolsky - Rosen (EPR) formulada por ellos utiliza un experimento mental similar al que acabamos de describir para concluir: la mecánica cuántica no puede ser una descripción completa de la realidad. Ahora, basándose en la investigación teórica que siguió, y en muchas mediciones, se ha establecido una opinión común de que la paradoja de EPR contiene un error y que la teoría cuántica es correcta. El enredo mecánico-cuántico es real: las mediciones de los sistemas enredados se correlacionarán, incluso si estos sistemas están muy separados en el espacio-tiempo.

Volvamos a la situación en la que colocamos dos electrones en un estado spin-singlete y los distribuimos a Alice y Bob. ¿Qué podemos decir sobre los electrones antes de tomar medidas? Que ambos juntos están en un cierto estado cuántico (spin-singlete). El giro del electrón Alicina es igualmente probable que se dirija hacia arriba o hacia abajo. Más precisamente, el estado cuántico de su electrón con la misma probabilidad puede ser uno (girar hacia arriba) u otro (girar hacia abajo). Ahora para nosotros, el concepto de probabilidad adquiere un significado más profundo que antes. Antes, consideramos un cierto estado cuántico (el estado fundamental de un átomo de hidrógeno) y vimos que hay algunas preguntas "incómodas", como "¿Dónde está ubicado el electrón?", Preguntas cuyas respuestas existen solo en un sentido probabilístico. Si hiciéramos preguntas "buenas", por ejemplo: "¿Cuál es la energía de este electrón?", Obtendríamos ciertas respuestas para ellos. Ahora no hay preguntas "buenas" que podamos hacer sobre el electrón de Alice, cuyas respuestas no dependerían del electrón de Bob. (No estamos hablando de preguntas estúpidas como "¿Tiene el electrón de Alice un giro?", Preguntas para las que solo hay una respuesta). Por lo tanto, tendremos que usar un lenguaje probabilístico para determinar los parámetros de uno de los sistemas medio confundidos. La certeza surge solo cuando consideramos la conexión entre las preguntas que Alice y Bob pueden hacer sobre sus electrones.

Comenzamos a propósito con uno de los sistemas de mecánica cuántica más simples que conocemos: los sistemas de espín de electrones individuales. Se espera que las computadoras cuánticas se construyan sobre la base de sistemas tan simples. El sistema de espín de electrones individuales u otros sistemas cuánticos equivalentes ahora se llaman qubits (abreviatura de "bits cuánticos"), que enfatiza su papel en las computadoras cuánticas, similar al papel desempeñado por los bits ordinarios en las computadoras digitales.

Imagine ahora que hemos reemplazado cada electrón con un sistema cuántico mucho más complejo con muchos y no solo dos estados cuánticos. Por ejemplo, le dieron barras de magnesio puro a Alice y Bob. Antes de que Alice y Bob se separen en diferentes direcciones, sus barras pueden interactuar, y acordaremos que al hacerlo adquieren un cierto estado cuántico general. Tan pronto como Alice y Bob divergen, sus barras de magnesio dejan de interactuar. Como en el caso de los electrones, cada barra está en un estado cuántico indefinido, aunque juntas, como creemos, forman un estado completamente definido. (En esta discusión, suponemos que Alice y Bob pueden mover sus barras de magnesio sin alterar su estado interno, tal como supusimos anteriormente que Alice y Bob podían separar sus electrones enredados sin cambiar sus espines). Pero la diferencia entre este experimento mental y el experimento con electrones es que la incertidumbre en el estado cuántico de cada barra es enorme. Una barra bien puede adquirir más estados cuánticos que el número de átomos en el universo. Aquí es donde la termodinámica entra en escena. Sin embargo, los sistemas muy imprecisos pueden tener algunas características macroscópicas bien definidas. Tal característica es, por ejemplo, la temperatura. La temperatura es una medida de la probabilidad con la que cualquier parte de un sistema tiene una cierta energía promedio, con una temperatura más alta que corresponde a una mayor probabilidad de tener más energía. Otro parámetro termodinámico es la entropía, que es esencialmente igual al logaritmo del número de estados que puede tomar el sistema. Otra característica termodinámica que sería significativa para una barra de magnesio es su magnetización total, que es, en esencia, un parámetro que muestra cuánto más electrones puede haber en la barra con el giro apuntando hacia arriba que con el giro apuntando hacia abajo.

Hemos involucrado la termodinámica en nuestra historia como una forma de describir sistemas cuyos estados cuánticos no se conocen exactamente debido a su enredo con otros sistemas. La termodinámica es una herramienta poderosa para analizar tales sistemas, pero sus creadores no esperaban tal aplicación. Sadi Carnot, James Joule, Rudolph Clausius fueron los líderes de la revolución industrial del siglo XIX y estaban interesados ​​en sus preguntas más prácticas: ¿cómo funcionan los motores? La presión, el volumen, la temperatura y el calor son la carne y la sangre de los motores. Carnot descubrió que la energía en forma de calor nunca puede convertirse por completo en un trabajo útil como levantar mercancías. Parte de la energía siempre se desperdiciará. Clausius hizo la principal contribución a la creación de la idea de la entropía como una herramienta universal para determinar las pérdidas de energía durante cualquier proceso asociado con el calor. Su principal logro fue darse cuenta de que la entropía nunca disminuye, en casi todos los procesos crece. Los procesos en los que aumenta la entropía se denominan irreversibles, precisamente porque no pueden revertirse sin disminuir la entropía. Clausius, Maxwell y Ludwig Boltzmann (entre muchos otros) dieron el siguiente paso en el desarrollo de la mecánica estadística: demostraron que la entropía es una medida del desorden. Por lo general, cuanto más actúas en algo, más te equivocas allí. E incluso si ha desarrollado un proceso cuyo objetivo es restablecer el orden, inevitablemente se formará más entropía de la que se destruirá, por ejemplo, cuando se libera calor. La grúa, que apila las vigas de acero en perfecto orden, crea orden en términos de la ubicación de las vigas, pero se liberará tanto calor durante su funcionamiento que la entropía total aún aumenta.

Pero aún así, la diferencia entre la visión sobre la termodinámica de los físicos del siglo XIX y la visión asociada con el enredo cuántico no es tan grande como parece. Cada vez que un sistema interactúa con un agente externo, su estado cuántico se confunde con el estado cuántico del agente. Por lo general, este enredo conduce a un aumento en la incertidumbre del estado cuántico del sistema, en otras palabras, a un aumento en el número de estados cuánticos en los que puede estar el sistema. Como resultado de la interacción con otros sistemas, la entropía, definida en términos de la cantidad de estados cuánticos disponibles para el sistema, generalmente crece.

En general, la mecánica cuántica proporciona una nueva forma de caracterizar los sistemas físicos en los que algunos parámetros (p. Ej., Posición en el espacio) se vuelven inciertos, mientras que otros (p. Ej., Energía) a menudo se conocen con exactitud. En el caso del enredo cuántico, dos partes fundamentalmente separadas del sistema tienen un estado cuántico común conocido, y cada parte por separado es un estado indefinido. Un ejemplo estándar de enredo es un par de giros en un estado singlete en el que es imposible decir qué giro está dirigido hacia arriba y cuál está hacia abajo.La incertidumbre del estado cuántico en un sistema grande requiere un enfoque termodinámico en el que los parámetros macroscópicos, como la temperatura y la entropía, se conocen con gran precisión, a pesar de que el sistema tiene muchos posibles estados cuánticos microscópicos.

Después de terminar nuestra breve excursión en el campo de la mecánica cuántica, el enredo y la termodinámica, intentemos ahora comprender cómo todo esto conduce a una comprensión del hecho de que los agujeros negros tienen temperatura. El primer paso hacia esto fue hecho por Bill Unruh: demostró que un observador acelerador en un espacio plano tendrá una temperatura igual a su aceleración dividida por 2π. La clave para los cálculos de Unruh es que un observador que se mueve con aceleración constante en una determinada dirección solo puede ver la mitad del espacio-tiempo plano. La segunda mitad, de hecho, se encuentra más allá del horizonte, similar al horizonte de un agujero negro. Al principio parece imposible: ¿cómo puede el espacio-tiempo plano comportarse como un horizonte de agujero negro? Para entender cómo va esto, pedimos la ayuda de nuestros observadores fieles Alice, Bob y Bill.A pedido nuestro, se alinean, con Alice encontrándose entre Bob y Bill, y la distancia entre los observadores en cada par es exactamente de 6 kilómetros. Se acordó que a tiempo cero, Alice se lanzaría a un cohete y volaría hacia Bill (y, por lo tanto, desde Bob) con aceleración constante. Tiene un cohete muy bueno, capaz de acelerar 1,5 billones de veces más que la aceleración gravitacional con la que los objetos se mueven cerca de la superficie de la Tierra. Por supuesto, no es fácil para Alice resistir tal aceleración, pero, como veremos ahora, estas cifras se eligen para un propósito específico; después de todo, solo estamos discutiendo las potencialidades, eso es todo. Exactamente en el momento en que Alice salta a su cohete, Bob y Bill agitan la mano. (Tenemos derecho a usar la expresión "exactamente en el momento en que ...", porque si bien Alice aún no ha comenzado a volar,ella está en el mismo marco de referencia que Bob y Bill, para que todos puedan sincronizar sus relojes.) Alice, por supuesto, la ve saludando: si está en el cohete, lo verá antes de que esto suceda, si se quedaba donde estaba, porque su cohete con ella vuela precisamente hacia él. Por el contrario, ella se está alejando de Bob, por lo que podemos suponer razonablemente que verá cómo él la saluda, un poco más tarde de lo que hubiera visto, si se hubiera quedado en su antiguo lugar. Pero la verdad es aún más sorprendente: ¡no verá a Bob en absoluto! En otras palabras, los fotones que vuelan desde Bob saludando a Alice nunca la alcanzarán, incluso teniendo en cuenta que nunca podrá alcanzar la velocidad de la luz. Si Bob comenzó a saludar, estando un poco más cerca de Alice, entonces los fotones que volaron lejos de él en el momento de su partida la habrían alcanzado.y si él estaba un poco más lejos, entonces aún más para que no lo alcanzaran. Es en este sentido que decimos que solo la mitad del espacio-tiempo es visible para Alice. En el momento en que Alice comienza a moverse, Bob está un poco más allá del horizonte que Alice observa.

En nuestra discusión sobre el entrelazamiento cuántico, ya estamos acostumbrados a la idea de que incluso si un sistema mecánico cuántico en su conjunto tiene un cierto estado cuántico, algunas partes del mismo pueden no tenerlo. De hecho, cuando hablamos de un sistema cuántico complejo, una parte de él se puede caracterizar mejor precisamente en el marco de la termodinámica: se le puede atribuir una temperatura muy definida, a pesar del estado cuántico altamente indefinido de todo el sistema. Nuestra última historia sobre Alice, Bob y Bill es un poco similar a esta situación, pero el sistema cuántico del que estamos hablando aquí es un espacio-tiempo vacío, y Alice solo ve la mitad. Hacemos una reserva de que el espacio-tiempo en su conjunto está en su estado fundamental, lo que significa la ausencia de partículas en él (por supuesto, sin contar a Alice, Bob,Bill y cohetes). Pero esa parte del espacio-tiempo que Alice ve no estará en el estado fundamental, sino en un estado confundido con esa parte que ella no ve. El espacio-tiempo percibido de Alice se encuentra en un complejo estado cuántico indefinido caracterizado por una temperatura finita. Los cálculos de Unruh muestran que esta temperatura es de aproximadamente 60 nanokelvin. En resumen, mientras acelera, Alice se sumerge en un baño tibio de radiación con una temperatura igual (en unidades apropiadas) a la aceleración dividida porcaracterizado por la temperatura final. Los cálculos de Unruh muestran que esta temperatura es de aproximadamente 60 nanokelvin. En resumen, mientras acelera, Alice, por así decirlo, se sumerge en un baño de radiación tibia con una temperatura igual (en unidades apropiadas) a la aceleración dividida porcaracterizado por la temperatura final. Los cálculos de Unruh muestran que esta temperatura es de aproximadamente 60 nanokelvin. En resumen, mientras acelera, Alice, por así decirlo, se sumerge en un baño de radiación tibia con una temperatura igual (en unidades apropiadas) a la aceleración dividida por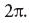



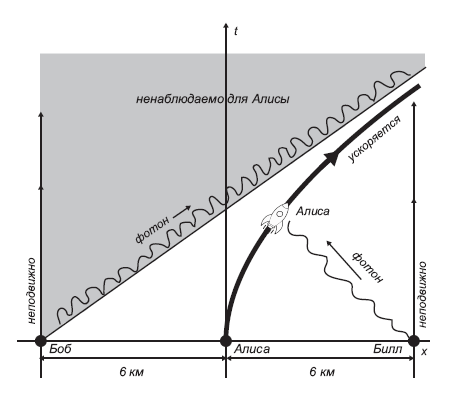
Fig. 7.1.Alice se mueve con aceleración desde un estado de reposo, mientras que Bob y Bill permanecen inmóviles. La aceleración de Alice es tal que nunca ve los fotones que Bob envía en su dirección en el momento t = 0. Sin embargo, recibe los fotones que en el momento t = 0 Bill la envió. El resultado es que Alice solo puede observar la mitad del espacio-tiempo.

Lo extraño de los cálculos de Unruh es que, aunque se refieren al espacio vacío de principio a fin, contradicen las famosas palabras del Rey Lear "nada saldrá de la nada". ¿Cómo puede ser tan complicado el espacio vacío? ¿De dónde pueden venir las partículas? El hecho es que, según la teoría cuántica, el espacio vacío no está vacío. Aquí y allá, las excitaciones de corta duración, llamadas partículas virtuales, cuya energía puede ser tanto positiva como negativa, aparecen y desaparecen constantemente. Un observador del futuro lejano, llamémosla Carol, que puede ver casi todo el espacio vacío, puede confirmar que no hay partículas permanentemente existentes en él. Además, la presencia de partículas con energía positiva en esa parte del espacio-tiempo que Alice puede observar,debido al enredo cuántico, se asocia con excitaciones de energía de signo igual y opuesto en una parte no observable del espacio-tiempo. Toda la verdad sobre el espacio-tiempo vacío en su conjunto está abierta a Carol, y esta verdad es que no hay partículas. Sin embargo, la experiencia de Alice le dice que hay partículas.

Pero luego resulta que la temperatura calculada por Unruh parece ser solo una ficción: no es tanto una propiedad del espacio plano como tal, sino una propiedad de un observador que experimenta una aceleración constante en el espacio plano. Sin embargo, la gravitación en sí misma es la misma fuerza "ficticia" en el sentido de que la "aceleración" que causa no es más que un movimiento a lo largo de una geodésica en una métrica curva. Como explicamos en el Capítulo 2, el principio de equivalencia de Einstein es que la aceleración y la gravedad son esencialmente equivalentes. Desde este punto de vista, no hay nada particularmente impactante en que el horizonte de un agujero negro tenga una temperatura igual a la temperatura del observador acelerado calculada por Unru. Pero podemos preguntar¿Qué valor de aceleración debemos usar para determinar la temperatura? Moviéndonos a una distancia suficientemente grande del agujero negro, podemos hacer que su atracción gravitacional sea arbitrariamente débil. ¿Se deduce que para determinar la temperatura efectiva del agujero negro que estamos midiendo, necesitamos usar el valor de aceleración pequeño correspondiente? Esta pregunta resulta bastante insidiosa porque, como creemos, la temperatura de un objeto no puede disminuir arbitrariamente. Se supone que tiene un valor finito fijo que incluso un observador muy distante puede medir.¿Qué necesitamos para usar el valor de aceleración pequeño correspondiente para determinar la temperatura efectiva del agujero negro que estamos midiendo? Esta pregunta resulta bastante insidiosa porque, como creemos, la temperatura de un objeto no puede disminuir arbitrariamente. Se supone que tiene un valor finito fijo que incluso un observador muy distante puede medir.¿Qué necesitamos para usar el valor de aceleración pequeño correspondiente para determinar la temperatura efectiva del agujero negro que estamos midiendo? Esta pregunta resulta bastante insidiosa porque, como creemos, la temperatura de un objeto no puede disminuir arbitrariamente. Se supone que tiene un valor finito fijo que incluso un observador muy distante puede medir.