🗳️ 🈂️ 🍱 Entropía informativa del caos 🖐️ 🤥 🈺

Introduccion

Hay muchas publicaciones sobre Habr en las que se considera el concepto de entropía, aquí hay algunas de ellas [1 ÷ 5]. Las publicaciones fueron recibidas positivamente por los lectores y despertaron un gran interés. Es suficiente para dar la definición de entropía dada por el autor de la publicación [1]: "entropía es la cantidad de información que no se conoce sobre el sistema". Las publicaciones sobre el fenómeno del caos en Habr también son suficientes [6–9]. Sin embargo, no se consideró la relación de entropía y caos en ambos grupos de publicaciones.

Esto se debe al hecho de que diferentes áreas del conocimiento distinguen diferentes tipos de medidas de caos:

informativo;
termodinámica
diferencial
cultural

Las medidas del caos también se describen teniendo en cuenta su especificidad, incluso en una de estas áreas es bastante difícil.

Intentando simplificar la tarea lo máximo posible, decidí considerar la relación entre la entropía informativa y el caos usando el ejemplo de la similitud de las regiones de paso del orden al caos en los diagramas en forma de mapeos de puntos y en los gráficos del coeficiente de entropía para estas regiones.

Lo que surgió de esto lo aprenderá mirando debajo del gato.

Los mecanismos de transición del orden al caos

Un análisis de los mecanismos de la transición del orden al caos en sistemas reales y varios modelos ha revelado la versatilidad de relativamente pocos escenarios de transición al caos. La transición al caos se puede representar en forma de diagrama de bifurcación (el término "bifurcación" se utiliza para denotar reordenamientos cualitativos del sistema con la aparición de un nuevo modo de su comportamiento).

La entrada del sistema en modo impredecible se describe mediante una cascada de bifurcaciones que siguen una tras otra. La cascada de bifurcaciones conduce secuencialmente a una elección entre dos soluciones, luego cuatro, etc., el sistema comienza a oscilar en un modo caótico y turbulento de duplicar secuencialmente el número de valores posibles.

Consideramos las bifurcaciones de duplicación de períodos y la aparición de caos en los mapeos de puntos. La pantalla es una función que muestra la dependencia de los siguientes valores de los parámetros del sistema con los valores anteriores:

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$

Considere también la segunda función de uso común:

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Usando mapeos de puntos, los objetos se estudian no con tiempo continuo, sino con tiempo discreto . Tras la transición a la pantalla, la dimensión del sistema en estudio puede disminuir.

Al cambiar el parámetro externo \ lambda, los mapeos de puntos exhiben un comportamiento bastante complicado, que se vuelve caótico con \ lambda suficientemente grande. El caos es una recesión muy rápida de trayectorias en el espacio de fase.

La bifurcación es una reestructuración cualitativa de la película. Los valores del parámetro de control en el que ocurren las bifurcaciones se denominan valores críticos o de bifurcación.

Para construir los diagramas, usaremos los siguientes dos listados:

No 1. Para la función:

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$

Listado de programa

# -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=(a-1)/a#     def ff(x):#  return a*x*(1-x) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

No. 2. Para la función

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Listado de programa

 # -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=((a-1)/a)**0.5 def ff(x):#  return a*x*(1-x**2) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n}^{2})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

Evaluar el impacto de la naturaleza de la función logística en los valores críticos.

$\ lambda$ considerar diagramas con una función

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ para esto usaremos el listado No. 1:

Para 0 <\ lambda <1 para

$\ lambda = $ 0.9$ y x0 = 0.47 obtenemos el diagrama:

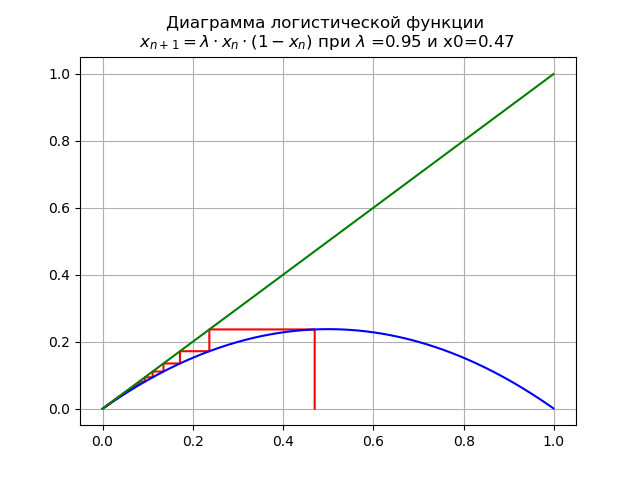
En este caso, el mapa tiene un único punto fijo

$x ^ {*} = 0$
que es sostenible

En

$1 <\ lambda <3$ para

$\ lambda = $ 2.$ x0 = 0.7 obtenemos el diagrama:

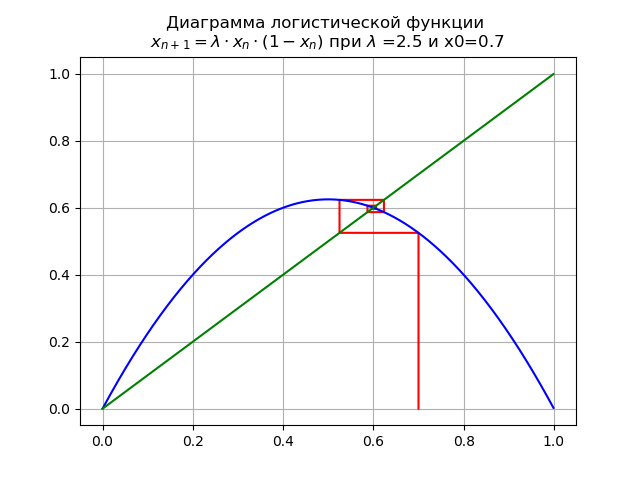
En el segmento [0, 1], aparece otro punto fijo fijo

$x_ {1} ^ {*} = 1-1 / \ lambda$

En

$1 <\ lambda <3$ para

$\ lambda = $ 2.$ y x0 = 0.01 obtenemos el diagrama:

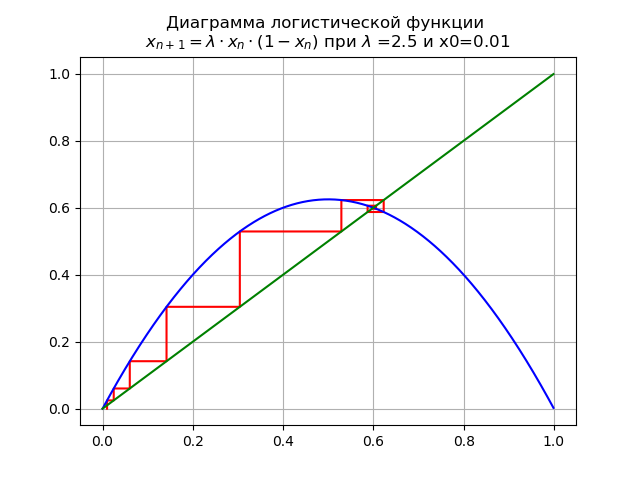
Punto fijo

$x ^ {*} = 0$ pierde estabilidad

En

$3 <\ lambda <3.45$ para

$\ lambda = $ 3.4$ y x0 = 0.7 obtenemos el diagrama:

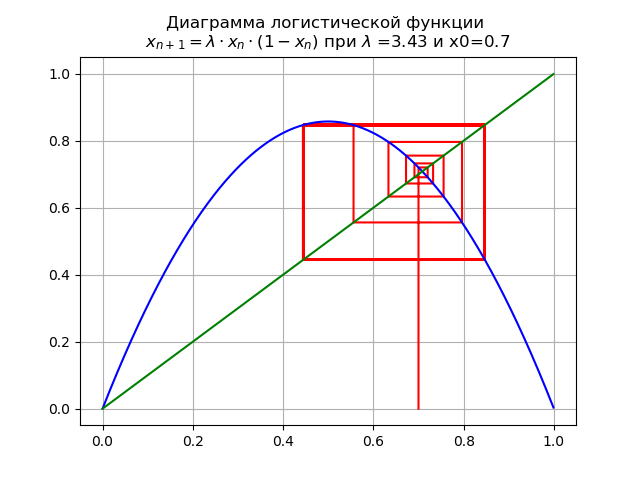
El mapeo sufre una bifurcación: punto fijo

$x_ {1} ^ {*}$ se vuelve inestable y aparece un doble ciclo en su lugar.

En

$3.45 <\ lambda <4.0$ para

$\ lambda = $ 3.5$
y x0 = 0.2 obtenemos el diagrama:

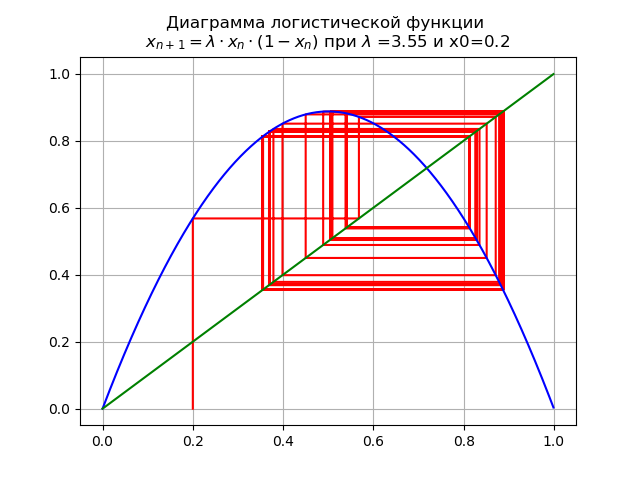
Al pasar un parámetro

$\ lambda$ a través del valor

$\ lambda = 3.45$ , Un ciclo de 2 veces se convierte en 4 veces, y más allá.

Al valor final

$\ lambda = 4$ El sistema tiene ciclos inestables de todos los pedidos posibles:

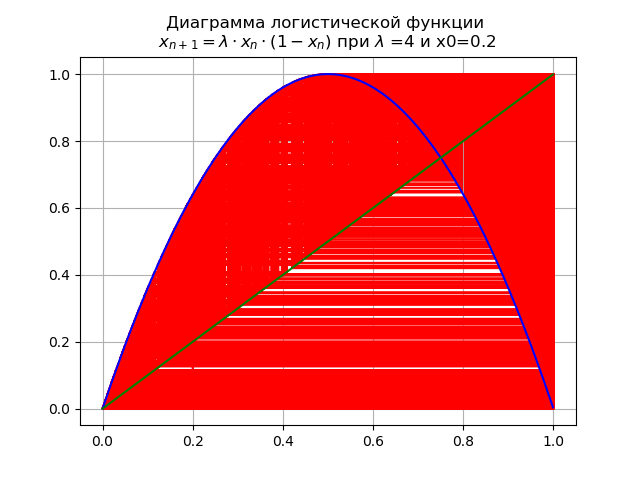
Evaluar el impacto de la naturaleza de la función logística en los valores críticos.

$\ lambda$ considerar diagramas con una función

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$ , para esto utilizaremos el listado No. 2.

En

$0 <\ lambda <= 1.0$ para

$\ lambda = 0.5$ y x0 = 0.2:

El mapeo tiene un solo punto fijo

$x ^ {*} = 0$ que es sostenible

En

$1 <\ lambda <= 1.998 ...$ para

$\ lambda = $ 1.$ y x0 = 0.55:

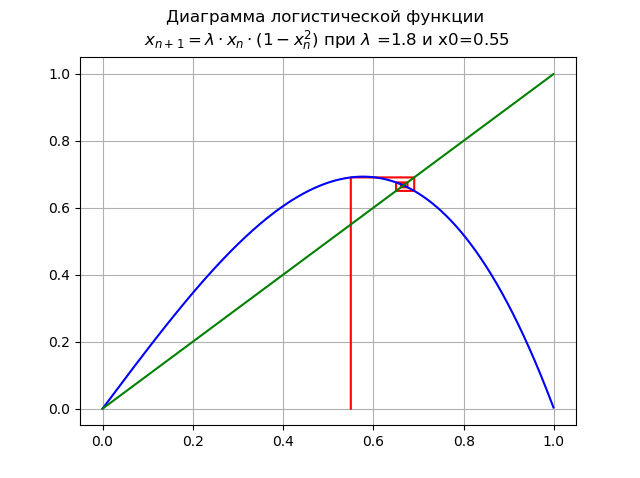
Punto

$x ^ {*} = 0$ pierde estabilidad, aparece un nuevo punto estable

$x_ {1} ^ {*}$

En

$1.99 <\ lambda <= 2.235 ...$ para

$\ lambda = $ 2.$ y x0 = 0.2:

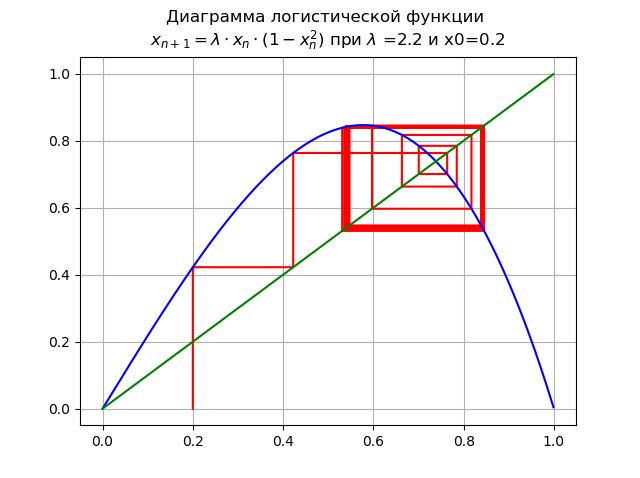
Se produce la bifurcación de la duplicación del período, aparece un ciclo de 2 veces. Aumento adicional

$\ lambda$ conduce a una cascada de bifurcaciones de período doble.

En

$2,235 <\ lambda 2.5980 ...$ para

$\ lambda = 2.287$ y x0 = 0.2:

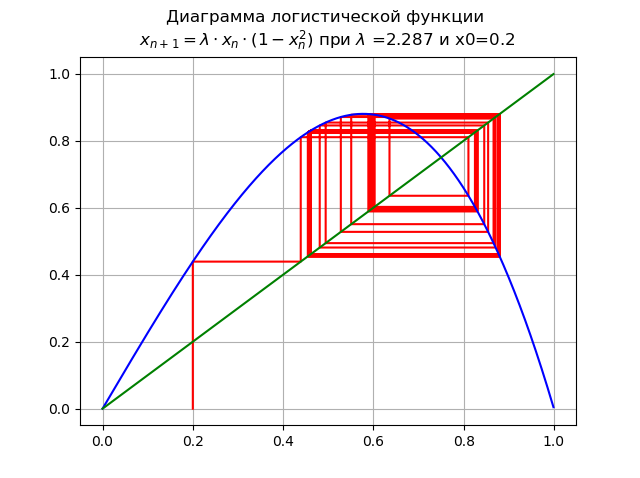
Aumentar

$\ lambda$ condujo a una cascada de bifurcaciones de período doble.

En

$\ lambda = 2.59$ El sistema tiene ciclos inestables de todos los períodos posibles:

Como se mostró en los diagramas, con un aumento en el orden de la función logística, el rango de cambio

$\ lambda$ se afila.

Usando diagramas, trazamos el camino desde el orden hasta el caos, mientras establecemos los valores

$\ lambda$ para diferentes funciones logísticas. Queda por responder la pregunta: ¿cómo medir el caos? Se conoce la respuesta para algunos de los tipos de caos enumerados al principio del artículo.
- La entropía es una medida del caos. Sin embargo, esta respuesta puede atribuirse completamente al caos de la información, qué entropía se aplica aquí y cómo comparar con el valor numérico ya considerado

$\ lambda$ - Intentaré responder esta pregunta en la siguiente parte del artículo.

Entropía de información y coeficiente de entropía

Consideraremos la entropía binaria de información para eventos aleatorios independientes.

$x$ c

$n$ posibles estados distribuidos con probabilidades

$p_ {i} (i = 1, .., n)$ . La entropía binaria de información se calcula mediante la fórmula:

$H (x) = - \ sum_ {i = 1} ^ {n} p_ {i} \ cdot log_ {2} (p_ {i})$

Este valor también se llama la entropía media del mensaje. Valor

$H_ {i} = - log_ {2} (p_ {i})$ llamado entropía privada, que caracteriza solo el i -ésimo estado. En el caso general, la base del logaritmo en la definición de entropía puede ser mayor que 1; Su elección determina la unidad de medida de la entropía.

Utilizaremos logaritmos decimales en los que la entropía y la información se miden en bits. La cantidad de información en bits se calculará correctamente cuando, por ejemplo, las variables

$X$ y

$\ Delta$ será sustituido en las expresiones correspondientes por entropía sin importar en qué, pero siempre en las mismas unidades. De hecho:

$q = H (x) -H (\ Delta) = log_ {10} \ left (X_ {2} -X_ {1} \ right) -log_ {10} (2 \ Delta) = log_ {10} (\ frac {X_ {2} -X_ {1}} {2 \ Delta})$

donde X y

$\ Delta$ debe estar en las mismas unidades.

Una estimación del valor de entropía de una variable aleatoria a partir de datos experimentales se encuentra a partir de un histograma de la siguiente relación:

$\ Delta_ {e} = \ frac {1} {2} e ^ {H (x)} = \ frac {d} {2} \ prod_ {i = 1} ^ {m} (\ frac {n} { n_ {i}}) ^ {\ frac {n_ {i}} {n}} = \ frac {dn} {2} 10 ^ {- \ frac {1} {n}} \ sum_ {i = 1} ^ {m} n_ {i} log_ {10} (n_ {i})$

donde:

$d$ –Ancho de cada columna del histograma;

$m$ - número de columnas;

$n$ -cantidad total de datos;

$n_ {i}$ - cantidad de datos en

$i$ esa columna

El coeficiente de entropía se determina a partir de la relación:

$k_ {e} = \ frac {\ Delta_ {e}} {\ sigma}$

donde:

$\ sigma$ - desviación estándar.

La entropía de la información como medida del caos

Para analizar los fenómenos del caos de información utilizando el coeficiente de entropía, primero creamos un diagrama de ramificación para la función

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ con la aplicación de áreas de transición obtenidas durante la construcción de histogramas:

Diagrama de rama

 import matplotlib.pyplot as plt import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(3.58,3.9,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-y[n-1]),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   3,6<= $\lambda$ <=3,9") plt.xlabel("r") plt.ylabel("$\lambda$ ") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.show()

Obtenemos:

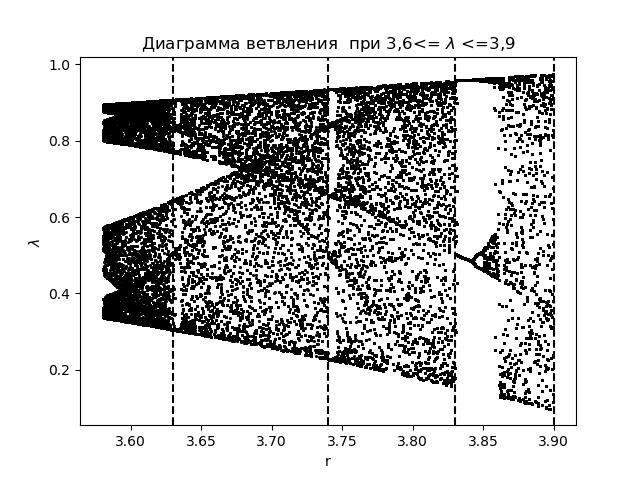
Trazamos el coeficiente de entropía para las mismas áreas.

$\ lambda$ :

El gráfico para el coeficiente de entropía

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(3.58,3.9,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-M[i-1,j]) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.title("  ke  3,6<= $\lambda$ <=3,9") plt.plot(arange(3.58,3.9,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.grid() plt.show()

Obtenemos:

Al comparar el diagrama y el gráfico, vemos una visualización idéntica de las regiones en el diagrama y en el gráfico para el coeficiente de entropía de la función

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ .

Para un análisis más detallado de los fenómenos del caos de información utilizando el coeficiente de entropía, creamos un diagrama de ramificación para la función logística:

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$ con la aplicación de áreas de transición:

Diagrama de rama

 import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(2.25,2.56,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-(y[n-1])**2),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   2.25<=$\lambda$ <=2.56") plt.xlabel("$\lambda$ ") plt.ylabel("y") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.show()

Obtenemos:

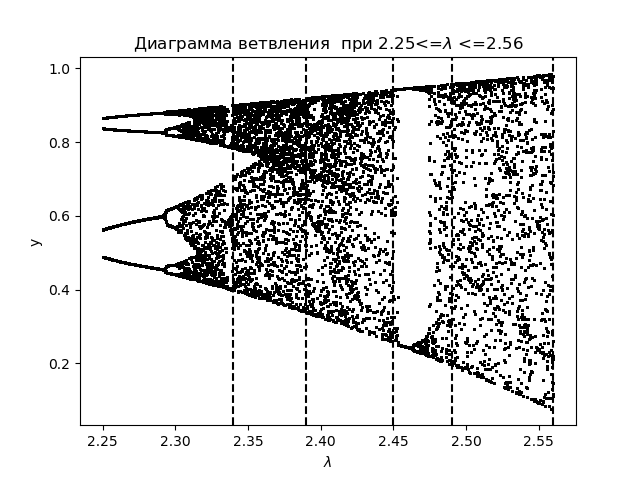
Trazamos el coeficiente de entropía para las mismas áreas.

$\ lambda$ :

Gráfico de coeficiente de entropía

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(2.25,2.56,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-(M[i-1,j])**2) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.figure(2) plt.title("  ke  2.25<= $\lambda$ <=2.56") plt.plot(arange(2.25,2.56,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.grid() plt.show()

Obtenemos:

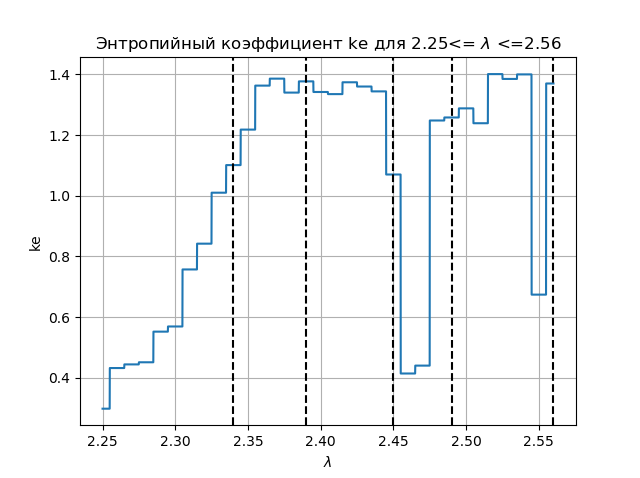
Al comparar el diagrama y el gráfico, vemos una visualización idéntica de las regiones en el diagrama y en el gráfico para el coeficiente de entropía de la función

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Conclusiones:

El problema educativo se resuelve en el artículo: la entropía informativa es una medida del caos, y Python da afirmativamente la respuesta a esta pregunta.

Entropía informativa del caos

Introduccion

Los mecanismos de transición del orden al caos

Entropía de información y coeficiente de entropía

La entropía de la información como medida del caos

Conclusiones:

Referencias

More articles: