En la estimación autorregresiva de la densidad espectral de una señal estacionaria

Los métodos de estimación espectral de procesos aleatorios estacionarios basados ​​en la transformación rápida de Fourier (FFT) son bien conocidos y ampliamente utilizados en la práctica de la ingeniería. Sus desventajas incluyen, en particular, una alta dispersión (baja precisión) de la estimación con un intervalo de observación insuficientemente largo para el proceso, que generalmente se manifiesta visualmente en un gráfico "indentado" de la densidad espectral de potencia (PSD). Uno de los métodos alternativos de estimación espectral es el método autorregresivo, considerado en el siguiente ejemplo, que es mucho menos conocido en la práctica de la ingeniería. En muchos casos, el método hace que sea relativamente fácil obtener una estimación mucho mejor de la PSD (Fig. 1) y, a veces, información aún más profunda sobre el proceso aleatorio en estudio.


Fig. 1 Evaluación clásica y autorregresiva del proceso "corto" PSD

Para fines de demostración, se sintetizó una señal de tiempo discreto (secuencia) x [i]. La señal se modela utilizando un modelo ARMA (filtro digital) que simula las propiedades de un sistema mecánico (1) - moviendo el punto de material x (t) en un oscilador de “masa única” con parámetros m = 1 kg, c = 100 N / m, k = 2, 5 kg / s, y por una perturbación de fuerza - ruido gaussiano "blanco" (teniendo en cuenta la discretización) f (t) con una dispersión de 1 N ² , el intervalo de muestreo en el tiempo Δt = 0,12 s.



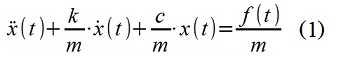
Modelo construido (2). El método de construcción del modelo ya se ha considerado anteriormente aquí .

x [i] - 0.6388 · x [i-1] + 0.7408 · x [i-2] = 0.009667 · f [i-1] (2)

Usando (2), se sintetizó una secuencia de 50 mil muestras, para lo cual se utilizó un generador de una variable aleatoria randn () distribuida normalmente de un entorno de software conocido.

Una vez completada la simulación del proceso x [i], se supone que los parámetros cuantitativos del modelo (2) son desconocidos: solo el proceso en sí y, en cierta medida, la información sobre las propiedades del modelo en los términos más generales están disponibles para la investigación.

Se realizó una estimación espectral de la secuencia de 50,000 puntos utilizando el método Welch, se tomó el tamaño del segmento igual a 256 muestras, se aplicó la ventana de Hamming y una superposición del 60% de los segmentos. La desviación estándar de dicha estimación, basada en el hecho de que la secuencia tiene una longitud de aproximadamente 200 segmentos no superpuestos, se puede estimar aproximadamente como ~ 7%.

Además, suponiendo que bajo condiciones reales en el experimento, una secuencia mucho más corta está disponible para la investigación, los estudios se llevaron a cabo solo en las primeras 500 muestras de esta señal.

Se obtiene una estimación por el método de Welch con los mismos parámetros. La desviación estándar de tal estimación es ~ 70%, se nota una "rugosidad" muy fuerte del gráfico (Fig. 2).


Fig. 2. Evaluación del PSD de los procesos "largos" y "cortos" por el método clásico.

En base al hecho de que conocemos la forma aproximada de la función (gráfico) del proceso SPM (por ejemplo, en función de la naturaleza física conocida del proceso: un oscilador de masa única bajo ruido blanco, o de evaluar procesos similares para los que hay implementaciones más largas disponibles), decidimos evaluar con utilizando el modelo autorregresivo de segundo orden (AR (2), o = ARMA (2.0)).

Determinar el orden del modelo es un punto muy importante; un error en el orden puede conducir a errores muy graves en los resultados de la estimación. Existen métodos que aún no se consideran aquí, que ayudan a determinar el orden del modelo basándose únicamente en el proceso que se analiza.

La estimación de los parámetros del modelo se realizó utilizando las conocidas ecuaciones de Yule-Walker para el proceso autorregresivo (ligeramente modificado para simplificar ligeramente la estructura del guión):



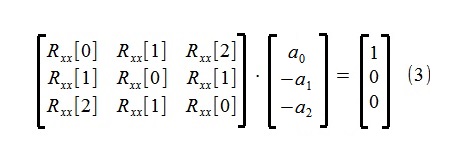
Como se puede ver en las ecuaciones, para determinar los parámetros, solo se utilizan los primeros tres miembros de la secuencia autorregresiva Rxx [0], Rxx [1], Rxx [2], que se estimaron a partir de la secuencia inicial de 500 puntos x [i] mediante el método de correlograma. ~ 4.5%.

(Por cierto, está claro que los "contras" antes de ₁ , a2 ₂ , etc., son extremadamente inconvenientes. Aparecieron debido al uso predominantemente "predictivo" de modelos ARMA en la economía, en sus fuentes anteriores de "ingeniería" No. Ya dudo que fuera necesario utilizar tal comprensión de los coeficientes AR aquí).

La matriz de correlación en (3) en la práctica siempre tiene una prevalencia diagonal estricta | Rxx [0] | > | Rxx [i] |, incluso debido a la presencia de ruidos de observación, como resultado de lo cual no hay dificultades con su manejo (encontrar una solución (3)).

(Para aclarar la cuestión de la magnitud del error de modelado estadístico, es interesante mencionar, por ejemplo, la estimación Rxx [0] = 2.2606e-04 m ² obtenida de 500 muestras, en comparación con las estimaciones de dispersión obtenidas del correlograma de 50,000 muestras, = 2.4238e-04 m ² y la estimación por el integrando del área PSD obtenida por el método Welch para 50,000 muestras (Fig. 2), = 2.4232e-04 m ² )

Después de sustituir las estimaciones encontradas Rxx [i] tenemos:



Los siguientes parámetros del modelo se determinan a ₀ = 11325.9; a ₁ = 7090,1; a ₂ = -8411.5; Como se puede ver en (3), la dispersión del hipotético ruido blanco entrante se estableció = 1 aquí, determinando en lugar de ello la ganancia a ₀ . La transformación de Fourier construye una estimación autorregresiva de la PSD sobre una secuencia de coeficientes a ₀ , a ₁ , a ₂ :




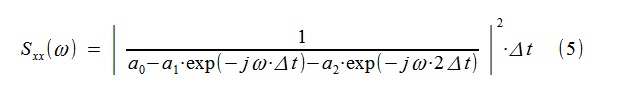
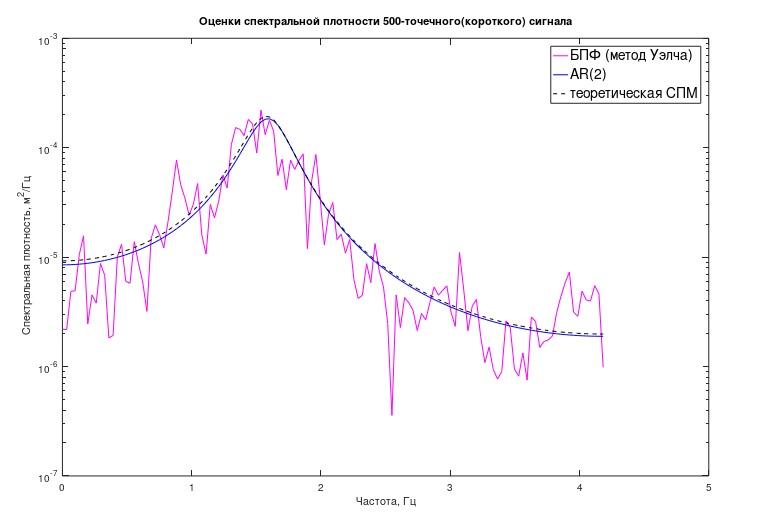Fig. 3 Evaluación clásica y autorregresiva del proceso "corto" PSD

De la misma manera, de acuerdo con una expresión similar a (5), el programa "teórico" del PSD se construyó anteriormente, solo los coeficientes del modelo allí, por supuesto, se tomaron de manera diferente (de (2)).
Se puede ver en el gráfico que la estimación de AR del PSD resultó ser muy cercana a la teóricamente esperada. Además del gráfico, es posible intentar evaluar algunas características analíticas del proceso y el sistema mecánico asociado. En este caso, estos son los "polos" del modelo, caracterizando numéricamente las frecuencias de los picos "resonantes" del modelo y los "factores de calidad" asociados.

De (5) encontramos la relación para buscar discontinuidades de la función de transferencia de nuestro modelo usando la transformada de Laplace (reemplazando jω por λ = -ε + jω):



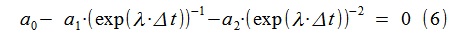
Para el modelo AR obtenido, λ _1,2 = -1.5427 ± j · 10.1514 se calculó de esta manera, que está muy cerca del modelo original utilizado para generar el proceso
λ _1.2theor = -1.2500 ± j · 9.9216 (es decir, las posiciones del pico de resonancia, respectivamente, 1.615 Hz (en teoría) y 1.579 Hz (determinado)).


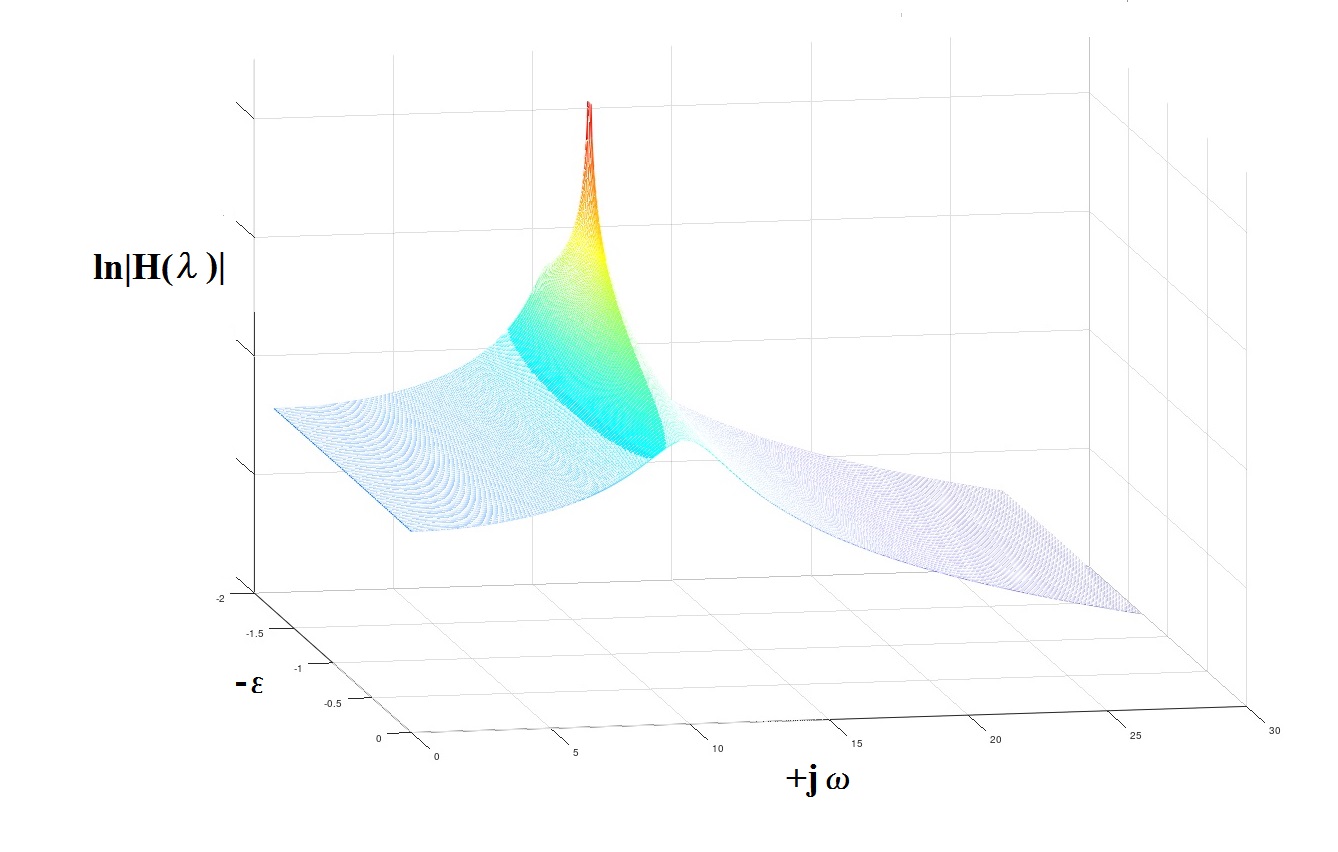Fig. 4 Sobre el concepto de "polos"

Algunos comentarios y recomendaciones en conclusión.

1. El orden "excesivo" (demasiado grande) del modelo AR suele ser mucho menos peligroso que insuficiente, desde el punto de vista del riesgo de obtener una estimación de PSD con errores graves.
2. Como regla, el modelado AR hace posible determinar con bastante precisión las frecuencias resonantes jω _k y mucho menos determinar con precisión los anchos de los "picos" correspondientes -ε _k
3. ARMA: el modelo puede resultar en un orden (tamaño) mucho más pequeño que el modelo AR, que parece estar destinado a mejorar la precisión del modelo, según muchas fuentes. Sin embargo, evaluar la parte MA del modelo es mucho más difícil y generalmente puede incluir el primer paso para obtener un modelo AR de orden grande para transformarlo aún más en la parte MA. En relación con estas fuentes, también se expresa una opinión alternativa sobre la conveniencia de utilizar exactamente modelos AR para la estimación espectral, aunque de un orden superior.
4. Para procesos muy cortos, así como para procesos no estacionarios, en lugar de la matriz de estimaciones de la función de autocorrelación, la matriz de covarianza generalmente se usa en (3).
5. Para un estudio detallado del tema de la estimación espectral autorregresiva, S.L. Marple ml. "Análisis espectral digital y sus aplicaciones", M., Mir, 1990