
En la comunidad científica, la visualización de datos y el diseño de la teoría juegan un papel muy importante. Las herramientas que implementan comandos de LaTeX , como Markdown y MathJax, a menudo se utilizan para una presentación conveniente y hermosa de fórmulas.
Para Julia, también hay un conjunto de paquetes que le permiten usar la sintaxis de LaTeX y, junto con los medios de álgebra simbólica, obtenemos una herramienta poderosa para manejar fórmulas.
Descarga y conecta todo lo que necesitas para hoy
using Pkg Pkg.add("Latexify") Pkg.add("LaTeXStrings") Pkg.add("SymEngine") using Latexify, LaTeXStrings, Plots, SymEngine
LaTeXStrings
LaTeXStrings es un pequeño paquete que facilita la introducción de ecuaciones de LaTeX en literales de cadena de Julia. Al usar cadenas regulares en Julia para ingresar un literal de cadena con ecuaciones de LaTeX incrustadas, debe evitar manualmente todas las barras invertidas y signos de dólar: por ejemplo, $ \alpha^2 $ se escribe \$\\alpha^2\$ . Además, aunque IJulia es capaz de mostrar ecuaciones con formato LaTeX (a través de MathJax ), esto no funcionará con líneas regulares. Por lo tanto, el paquete LaTeXStrings define:
- La clase
LaTeXString (un subtipo de String ) que funciona como una cadena (para indexación, conversión, etc.), pero se muestra automáticamente como texto / látex en IJulia. - Macros de cadena
L"..." y L"""...""" que le permiten ingresar ecuaciones de LaTeX sin escapar de las barras diagonales inversas y los signos de dólar (y que le agregan signos de dólar si los omite).
S = L"1 + \alpha^2"
El REPL generará:
"\$1 + \\alpha^2\$"
y Jupyter mostrará:
1+ alpha2
La indexación funciona como líneas normales:
S[4:7] "+ \\a"
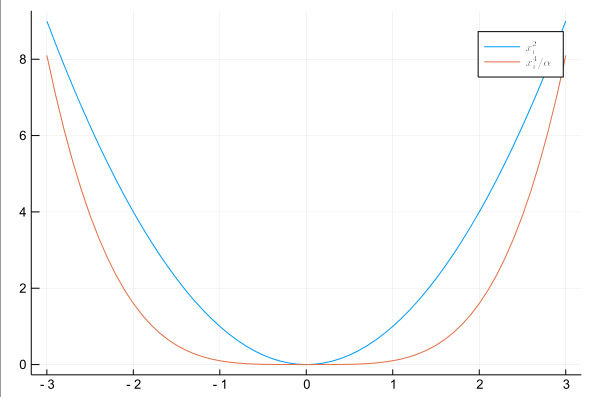
Dichas líneas pueden ser útiles en el diseño de gráficos.
x = [-3:0.1:3...] y1 = x .^2 α = 10 y2 = x .^4 / α; plot(x,y1, lab = "\$x^2_i\$") plot!(x,y2, lab = L"x^4_i/\alpha")
Latexify
Un paquete más funcional es Latexify ( Guía ). Está diseñado para generar matemáticas LaTeX a partir de objetos julia. Este paquete utiliza la homología de Julia para convertir expresiones en cadenas en formato LaTeX. Latexify.jl proporciona funciones para convertir una cantidad de diferentes objetos de Julia, que incluyen:
- Expresiones
- Cuerdas
- Números (incluidos racionales y complejos),
- Expresiones simbólicas de SymEngine.jl,
- ParameterizedFunctions y ReactionNetworks de DifferentialEquations.jl
así como matrices de todos los tipos compatibles.
ex = :(x/(y+x)^2)
fracx left(y+x right)2
str = "x/(2*k_1+x^2)"
fracx2 cdotk1+x2
Matriz de elementos heterogéneos:
m = [2//3 "e^(-c*t)" 1+3im; :(x/(x+k_1)) "gamma(n)" :(log10(x))] latexify(m)
\ left [\ begin {array} {ccc} \ frac {2} {3} & e ^ {- c \ cdot t} & 1 + 3 \ textit {i} \\ \ frac {x} {x + k_ {1}} & \ Gamma \ left (n \ right) & \ log_ {10} \ left (x \ right) \\ \ end {array} \ right]
\ left [\ begin {array} {ccc} \ frac {2} {3} & e ^ {- c \ cdot t} & 1 + 3 \ textit {i} \\ \ frac {x} {x + k_ {1}} & \ Gamma \ left (n \ right) & \ log_ {10} \ left (x \ right) \\ \ end {array} \ right]
Puede especificar una función que muestre fórmulas y las copie en el búfer de forma comprensible para Habr:
function habr(formula) l = latexify(formula) res = "\$\$display\$$l\$display\$\$\n" clipboard(res) return l end habr(ex)
fracx left(y+x right)2
<p>$<!-- math>$$display$$\frac{x}{\left( y + x \right)^{2}}$$display$$</math -->$</p>
Tener en cuenta
latexify("x/y") |> display
fracxy
latexify("x/y") |> print
$\frac{x}{y}$
Symengine
SymEngine es un paquete que proporciona cálculos simbólicos que puede visualizar en su Jupyter con Latexify.
Puede especificar caracteres en líneas y comillas ( quote ):
julia> a=symbols(:a); b=symbols(:b) b julia> a,b = symbols("ab") (a, b) julia> @vars ab (a, b)
Defina la matriz y visualícela bellamente
u = [symbols("u_$i$j") for i in 1:3, j in 1:3] 3×3 Array{Basic,2}: u_11 u_12 u_13 u_21 u_22 u_23 u_31 u_32 u_33 u |> habr
\ left [\ begin {array} {ccc} u_ {11} & u_ {12} & u_ {13} \\ u_ {21} & u_ {22} & u_ {23} \\ u_ {31} & u_ {32} & u_ {33} \\ \ end {array} \ right]
\ left [\ begin {array} {ccc} u_ {11} & u_ {12} & u_ {13} \\ u_ {21} & u_ {22} & u_ {23} \\ u_ {31} & u_ {32} & u_ {33} \\ \ end {array} \ right]
Supongamos que tenemos vectores
C = symbols("Ω_b/Ω_l") J = [symbols("J_$i") for i in ['x','y','z'] ] h = [0, 0, symbols("h_z")] 3-element Array{Basic,1}: 0 0 h_z
que debe ser multiplicado por vectores
using LinearAlgebra × = cross latexify(J×h, transpose = true)
$$ display $$ \ begin {ecation} \ left [\ begin {array} {c} J_ {y} \ cdot h_ {z} \\ - J_ {x} \ cdot h_ {z} \\ 0 \\ \ end {array} \ right] \ end {ecation} $$ display $$
Cálculos matriciales completos:
dJ = C*(u*J.^3)×h latexify( dJ, transpose = true) habr(ans)
$$ display $$ \ begin {ecation} \ left [\ begin {array} {c} \ frac {h_ {z} \ cdot \ left (u_ {21} \ cdot J_ {x} ^ {3} + u_ { 22} \ cdot J_ {y} ^ {3} + u_ {23} \ cdot J_ {z} ^ {3} \ right) \ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ \ frac { - h_ {z} \ cdot \ left (u_ {11} \ cdot J_ {x} ^ {3} + u_ {12} \ cdot J_ {y} ^ {3} + u_ {13} \ cdot J_ {z} ^ {3} \ right) \ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ 0 \\ \ end {array} \ right] \ end {ecuación} $$ display $$
pero con una cadena tan simple puedes encontrar el determinante y enviarlo a Habr
u |> det |> habr
u11 cdot left(u22− fracu12 cdotu21u11 right) cdot left(u33− fracu13 cdotu31u11− frac left(u23− fracu13 cdotu21u11 right) cdot left(u32− fracu12 cdotu31u11 right)u22− fracu12 cdotu21u11 right)
Recursivo! La matriz inversa probablemente se calcula de manera similar:
u^-1 |> habr
Spoiler$$ display $$ \ left [\ begin {array} {ccc} \ frac {1 - \ frac {u_ {12} \ cdot \ left (\ frac {- u_ {21}} {u_ {11}} - \ frac {\ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31 }} {u_ {11}} \ right)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) } \ right) \ cdot \ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {u_ {33} - \ frac {u_ {13 } \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ { 21}} {u_ {11}}}} derecha)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} - \ frac {u_ {13} \ cdot \ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31 }} {u_ {11}} \ right)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) } \ right)} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u _ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}}} {u_ {11}} & \ frac {\ frac {- u_ {12} \ cdot \ left (1 + \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {\ left (u_ {22 } - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} { u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} } \ right)} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} + \ frac {u_ {13} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {\ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21} } {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23 } - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} { u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ rig ht)}} {u_ {11}} & \ frac {\ frac {- u_ {13}} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12 } \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}} + \ frac { u_ {12} \ cdot \ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {\ left (u_ {22} - \ frac { u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ { 12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)} } {u_ {11}} \\ \ frac {\ frac {- u_ {21}} {u_ {11}} - \ frac {\ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right)} \ right) \ cdot \ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ { 12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}}} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} & \ frac {1 + \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} { \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)}} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} & \ frac {- \ left (u_ {23 } - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {\ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} { u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac { u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right )} \\ \ frac {\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ derecha)}} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} { u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}} & \ frac {- \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {\ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21 }} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)} & \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} { u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ c dot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ { 21}} {u_ {11}}} \ right) ^ {- 1} \\ \ end {array} \ right] $$ display $$
Si desea dañar su navegador Matjax, ponga menos el segundo grado (el cuadrado de la matriz inversa)
Por cierto, SymEngine considera derivados:
dJ[1] |> habr
frachz cdot left(u21 cdotJ3x+u22 cdotJ3y+u23 cdotJ3z right) cdot Omegab Omegal
diff(dJ[1], J[1]) |> habr
frac3 cdotJ2x cdothz cdotu21 cdot Omegab Omegal
Por cierto, Julia puede usar no solo fórmulas, sino también gráficos de LaTeX 'a. Y si instaló MikTex y ya descargó pgfplots , luego, utilizando el entorno apropiado, puede hacerse amigo de Julia, que le brindará la oportunidad de construir histogramas, gráficos tridimensionales, errores y relieves con contornos, y luego integrarlos en el documento LaTeX.
Eso es todo con fórmulas, pero no con cálculos simbólicos: Julia todavía tiene soluciones más complejas e interesantes para el álgebra simbólica, que definitivamente trataremos en algún momento la próxima vez.