Sobre la proximidad de los picos

“Antes de comprender esto, parece un milagro. Pero después de eso no hay nada especial ".

No, no sobre montañas, sobre cuentas. En matemáticas, hay preguntas cuya formulación es accesible para todos, pero la solución no es trivial y sin una preparación especial es difícil de explicar. Uno de estos problemas se puede expresar brevemente de la siguiente manera: ¿cómo calcular correctamente las distancias en gráficos dirigidos? Este problema un tanto abstracto puede reducirse a una tarea motivadora muy específica. Cabe en una imagen:

1. Declaración del problema. Yo vivo en uno, pero tú en el otro.

Una pequeña ciudad está dividida (por ejemplo, por un río, aunque en el contexto de los picos la garganta es más adecuada) en dos distritos (partes) $$$A$ y $$$B$ . La comunicación entre los distritos se lleva a cabo a lo largo de una sola carretera (puente), que tiene dos carriles: al lado de $$$A$ a $$$B$ y viceversa. En relación con el crecimiento de la población, surgió la cuestión de aumentar la capacidad de la carretera. El dinero, como siempre, es apenas suficiente y solo para un carril en una dirección. Está claro que incluso un solo carril acercará las regiones, pero la pregunta es ¿cuánto exactamente? Usted es un matemático urbano loco , y fue usted quien fue invitado para recibir una respuesta razonable .

¿Cuánto más cerca están las áreas si construyes otra franja en una dirección?

Redacción para avanzado

En lugar de los puentes de Konigsberg , se puede utilizar un lenguaje de teoría de grafos un poco más riguroso. Entonces, hay un gráfico dirigido con dos vértices (nodos) $$$A$ y $$$B$ . La magnitud de la conexión (conductividad, ancho de banda) en la dirección directa e inversa son inicialmente iguales. La pregunta es ¿cuánto cambiará la distancia entre los nodos si la conductividad en una de las direcciones se duplica?

Y sí, si usted es un verdadero soldador matemático, puede ofrecer (y justificar) una solución para cualquier valor directo y de retroalimentación. Idealmente, para un gráfico con cualquier número de nodos y enlaces.

Intimidad y andanzas borrachas

Está claro que la distancia habitual (kilómetro) entre regiones no depende de la presencia o ausencia de la carretera. Por lo tanto, no encaja aquí: debemos confiar en la comunicación. Cuantos más distritos estén conectados , cuanto más cerca estén, más residentes podrán llegar a otra área por unidad de tiempo.

Para evaluar la medida de proximidad entre nodos de un gráfico no dirigido, se puede utilizar la llamada distancia resistiva . Anteriormente, ya describimos las propiedades de esta distancia en el habr en varios artículos .

La distancia resistiva es equivalente al concepto de resistencia efectiva, cuando se trata de la red eléctrica. Por lo tanto, en lenguaje eléctrico, el problema puede formularse de la siguiente manera. Entre dos nodos, dos diodos de igual conductividad están conectados en sentido antihorario. ¿Cómo cambiará la resistencia entre estos puntos si agrega otro diodo? (Pido disculpas si el lenguaje eléctrico falló y escribí tonterías aquí).

Además, la resistencia efectiva se puede interpretar en el lenguaje de Markov para las probabilidades de caminatas aleatorias ebrias (para aquellos que deseen profundizar en el tema - google "Caminatas aleatorias y redes eléctricas").

La distancia resistiva es cuadrática, corresponde al cuadrado de la distancia lineal. Las distancias cuadráticas también se llaman quadrans . Pero dado que otras distancias (lineales) no se usan en este problema, no necesitamos el término quadrans aquí. (Hay suficiente lengua de pájaro incluso sin ella).

En general, el término "distancia resistiva" tampoco se ve bien. Él implica que estamos hablando de algún tipo de distancia inusual desconocida para la ciencia. De hecho, la distancia resistiva es la distancia euclidiana habitual. Pero en el espacio afín. Usamos esta característica más allá.

¿Y cuál es, de hecho, el problema?

Si sabemos qué es una "distancia resistiva", ¿por qué no podemos "simplemente tomarla y calcularla" para un gráfico dado?

Hm. En principio, fácil. Si estamos hablando de un gráfico no dirigido. Si la ciudad hubiera construido franjas en ambas direcciones, la distancia resistiva habría disminuido exactamente a la mitad. Dado que la resistencia es inversamente proporcional a la conductividad, y la conductividad (rendimiento) se ha duplicado. Y si agrego dos bandas en cada dirección, entonces la distancia disminuiría en 3 veces. Aquí todo es bastante trivial. (Y probablemente, alguien aquí ya puede adivinar la forma general de la solución. Y vamos más allá).

Cuando las relaciones opuestas no son iguales, entonces todo se complica. Y muy severamente.

No existe una forma legal, generalmente aceptada, de determinar la proximidad de los picos (distancias resistivas) en un gráfico direccional .

(Esta es mi tesis, tal vez alguien pueda convencerme). "No": aquí significa que no está en los libros de texto, wiki y en las cabezas (más precisamente, hay muchas formas diferentes de diferentes autores que requieren diferentes supuestos y definiciones). Hay una manera (aunque no tan simple). En este artículo, solo lo describimos.

La misma determinación de la distancia en presencia de conexiones dirigidas requiere aclaración si estamos hablando de un gráfico dirigido (métrica no conmutativa, me disculpo). Puedes hablar sobre la distancia desde $$$A$ antes $$$B$ , pero puedes desde $$$B$ antes $$$A$ . Y lo más probable es que estas distancias no siempre sean iguales. ¿De qué tipo de distancias estamos hablando en el problema?

Reglas de distancia euclidiana

Saldremos y respiraremos profundamente. Ya hemos mencionado que la distancia resistiva es la habitual Euclidiana. Esto significa que su definición puede reducirse a la definición de distancia euclidiana como la norma de la diferencia de dos elementos:

$$$S (A, B) = | A - B | ^ 2 = (A - B) ^ 2 = (A - B) \ cdot (A - B) = S (B, A) \ quad (1)$

Esta definición no depende del orden de los elementos: esta es la distancia conmutativa, la proximidad (más precisamente, la distancia) de los elementos. Un punto en una expresión significa una operación de producto escalar (espacio métrico). En consecuencia, la expresión (1) se puede revelar:

$$$S (A, B) = S (B, A) = A ^ 2 + B ^ 2 - A \ cdot B - B \ cdot A \ quad (2)$

Aqui $$$A ^ 2 = A \ cdot A$ , $$$B ^ 2 = B \ cdot B$ - normas de elementos. Cuando se trata de gráficos, las normas de los elementos suelen ser cero. En el problema original no se dice nada sobre las normas, por lo que puede tomarlas como cero (más sobre lo que significan las normas de los elementos en el espacio afín. Aquí , e incluso más detalles, aquí ). Entonces la expresión para la distancia deseada toma la forma:

$$$S (A, B) = - (A \ cdot B + B \ cdot A) = s_ {AB} + s_ {BA} \ quad (3)$

De acuerdo con la expresión (3), todo lo que se necesita para resolver el problema es encontrar los productos escalares de elementos (nodos) en un gráfico dirigido (es fácil de decir, pero ¿cómo hacer esto?).

En el camino, la fórmula (3) muestra que nuestra medida general (conmutativa) de proximidad entre elementos $$$A$ y $$$B$ es la suma de dos distancias dirigidas:

$$$s_ {AB} = - A \ cdot B$ - distancia direccional desde $$$A$ antes $$$B$ ,
$$$s_ {BA} = - B \ cdot A$ - distancia direccional desde $$$B$ antes $$$A$ .

2. La decisión. Largo camino en las dunas

El estruendo disminuyó. La diversión ha terminado. Luego vienen los detalles aburridos de la descripción de la esencia del método para calcular el producto escalar entre nodos de un gráfico dirigido. Esta es la parte que no sé cómo decir "de manera simple con los dedos". Pero aquí es donde lo más importante del artículo. Algo que vale la pena perder el tiempo.

La línea general de razonamiento es la siguiente. Con cuidado y sin emociones de nuevos supuestos adicionales, transferimos las propiedades conocidas de la métrica de los espacios simétricos a los asimétricos. Todo lo que se necesita es tener en cuenta las peculiaridades de la métrica en espacios afines.

Cualquier gráfico conectado (ya sea dirigido o no) define un espacio métrico afín. Algunas propiedades de dichos espacios en la ejecución simétrica (conmutativa) se describieron (de forma caótica) en la serie de artículos ya mencionada o, de manera más precisa y detallada, en el largo mencionado. No se apresure a cambiar: a continuación le damos (sin embargo, por el trabalenguas) los apretones principales.

Espacio métrico afinado (gráfico no dirigido)

Lo que es importante Bien conocido primero.

1. La afinidad del espacio significa que los conceptos de vector y elemento en el espacio son diferentes. El vector es la diferencia de elementos. Esta característica aparentemente insignificante conduce a consecuencias significativas si una métrica se define en el espacio.

2. El espacio se define por una base que consta de elementos. Los vértices del gráfico son la base del espacio. Las relaciones en un gráfico determinan sus propiedades métricas.

3. Una característica de conectividad gráfica es la matriz de adyacencia . Pero para las propiedades métricas (y otras), el laplaciano del gráfico (matriz de Kirchhoff) es más importante $$$L$ .

4. El laplaciano de un gráfico es un tensor casi métrico. "Casi" - aquí significa que está incompleto. Laplacian es una matriz degenerada y, por lo tanto, no es invertible. Y el tensor métrico estándar es completamente reversible.

Ahora menos conocido.

5. La diferencia entre elementos y vectores en un espacio afín métrico conduce a la existencia de un vector nulo en él $$$\ mathbb z$ . El producto escalar de elementos con un vector nulo en un espacio conmutativo (simétrico) es igual a la unidad (en un espacio no conmutativo depende de la dirección de multiplicación). Sin un vector cero, ¡el espacio del gráfico no está completo! Esto es importante

6. El centro ortogonal de la base es dual con respecto al vector nulo. $$$Z$ . Este es un elemento que es ortogonal a todos los demás elementos de la base (excepto el vector cero). Recuerde que la ortogonalidad de los elementos significa que su producto escalar es cero. El ortocentro de un triángulo es el círculo circunscrito . Sí, en un espacio afín completo, un elemento con una norma distinta de cero no es un punto, sino una esfera n-dimensional.

7. El laplaciano de la gráfica, junto con las coordenadas del centro ortogonal, se completa (un tensor métrico completo). En otras palabras, laplaciano completo $$$Lm$ Es un conde ordinario laplaciano $$$L$ pero limitado por las coordenadas barcéntricas del centro ortogonal.

8. La inversión del Laplaciano completo le permite a uno obtener un Gramian completo $$$Gm$ - la matriz de productos escalares de los elementos de la base (en nuestro caso, los vértices del gráfico). Este gramian es también un tensor métrico completo del espacio.

9. El encuadre de un gramiano completo es una tupla de unidades (productos escalares de elementos básicos y un vector cero). En la esquina - cero, esta es la norma del vector cero en sí.
La famosa matriz de Cayley-Menger es un Gramian casi regular.

Como resultado, concluimos que, según la reivindicación 8, el problema de determinar los productos escalares (y, por lo tanto, las distancias) entre los nodos de un gráfico se reduce a la determinación del tensor métrico inicial de la base $$$Gm$ .

Necesitamos un método para construir un gráfico gramiano completo $$$Gm$ para un laplaciano dado (incompleto) $$$L$ .

En el caso de los enlaces simétricos, la construcción de un Gramian completo del Laplaciano (y viceversa) no causa dificultades particulares. En este caso, los productos escalares de los elementos de la base y el vector cero son conmutativos, no dependen del orden de multiplicación:

$$$\ mathbb z \ cdot A = A \ cdot \ mathbb z = 1$

Para gráficos dirigidos (espacios no conmutativos) el problema es complicado. Aunque solo sea porque el número de conexiones posibles en el gráfico dirigido se duplica.

Espacio afín no conmutativo (gráfico dirigido)

Sobre las propiedades del Laplaciano del gráfico dirigido, también ya escribimos sobre el Habr . Dijeron cómo usar los potenciales de los laplacianos para clasificar objetos. En términos de bases, los potenciales del laplaciano son las coordenadas duales del vector cero (aniquilador del laplaciano).

En este artículo, estamos interesados ​​en propiedades métricas. Si se dirige el gráfico, entonces el producto escalar entre sus vértices depende del orden:

$$$A \ cdot B \ ne B \ cdot A$

Esto significa que las coordenadas duales en los gráficos dirigidos se dividen (en izquierda y derecha). Los valores de los productos escalares del vector cero y los elementos de la base (bordeando el gramático) también dependen del orden de los factores. Y por lo tanto, en contraste con el espacio conmutativo, aquí la mitad de las coordenadas duales del vector cero es desconocida y debe determinarse.

$$$\ mathbb z \ cdot A \ ne A \ cdot \ mathbb z$

Sin embargo, hay muchas cantidades conocidas.

En primer lugar, se conoce al propio laplaciano. Además, se sabe que la suma de sus filas es cero (en el caso general, este es un requisito opcional, pero para los laplacianos de gráficos dirigidos este suele ser el caso). También es importante que las coordenadas barcéntricas de los elementos sean únicas, ya que son independientes de la métrica del espacio. Es decir, el borde del Laplaciano del gráfico es simétrico tanto para el gráfico dirigido como para el gráfico no dirigido (no reconocí de inmediato este punto). Finalmente, conocemos las normas de los elementos de la base (generalmente en los gráficos son iguales a cero).

Queda por sustituir todo lo conocido y lo desconocido en la identidad que conecta al laplaciano y al gramático:

$$$Lm \ Gm = I$

Aqui $$$I$ Es una matriz de identidad. En esta identidad, el significado de la transición de un laplaciano incompleto a uno completo.

Cállate y cree

Pasemos de las palabras a los hechos. Así es como se ve el laplaciano $$$L$ para un gráfico de dos nodos:

$$$L = \ begin {bmatrix} c_1 & -c_1 \\ c_2 & -c_2 \ end {bmatrix}$

Para simplificar, hemos designado la relación con números: $$$c_1 = c_ {AB}, c_2 = c_ {BA}$ . Se supone que los valores de los enlaces son conocidos: a través de ellos expresaremos todas las demás cantidades.

Laplaciano completo $$$Lm$ incluye las coordenadas del ortocentro $$$[rz, az, bz]$ :

$$$Lm = \ begin {bmatrix} rz & az & bz \\ az & c_1 & -c_1 \\ bz & c_2 & -c_2 \ end {bmatrix}$

Aqui $$$rz$ - la norma del ortocentro (en el caso simétrico se interpreta como el cuadrado del radio), $$$az$ y $$$bz$ - coeficientes de expansión del ortocentro en la base $$$A, B$ (pesos barcéntricos).

Gramian completo $$$Gm$ Se parece a esto:

$$$Gm = \ begin {bmatrix} 0 & za & zb \\ 1 & 0 & g_1 \\ 1 & g_2 & 0 \ end {bmatrix}$

Aquí están las tuplas. $$$[za, zb]$ y $$$[1, 1]$ reflejan las coordenadas duales del vector nulo. Estas coordenadas son aniquiladores del laplaciano (cuando se multiplican por el laplaciano dan un vector cero, ¡no deben confundirse con un vector cero!).

Para resolver el problema, necesitamos encontrar la suma de los valores de gramian: $$$- (g_1 + g_2)$ .

Consideramos la cantidad de incógnitas: $$$rz, az, bz, za, zb, g_1, g_2$ - solo 7 (sí, sí - para averiguar el valor de una distancia desafortunada, necesitamos calcular siete valores adicionales más). Hay dos conexiones bien conocidas en la entrada: $$$c_1$ y $$$c_2$ . Identidad $$$Lm \ Gm = I$ dará 9 ecuaciones. Total 7 + 2 = 9, - todo converge (sorprendentemente). Queda por resolver simplemente el sistema de ecuaciones.

Para un gráfico de dos nodos, la solución (todas las incógnitas) se puede expresar en forma explícita. Damos expresiones finitas para las cantidades que nos interesan. Introducimos el concepto de conectividad geométrica general: este es el recíproco de la norma del centro ortogonal $$$gc = 1 / rz$ . Su dimensión coincide con la dimensión de los enlaces del gráfico. Para un gráfico de dos nodos (y dos conexiones), la conexión geométrica tiene una buena expresión:

$$$gc = 1 / rz = (\ sqrt {c_1} + \ sqrt {c_2}) ^ 2$

A través de esta conexión, se pueden expresar productos escalares de nodos:

$$$g_1 = -gc \ sqrt {c_2}, \ quad g_2 = -gc \ sqrt {c_1}$

Puedes traducir productos escalares $$$g$ en distancias direccionales $$$s$ (3):

$$$s_ {BA} = gc \ sqrt {c_ {AB}}; \ quad s_ {BA} = gc \ sqrt {c_ {AB}}$

La distancia conmutativa deseada entre los nodos está determinada por la suma:

$$$S (A, B) = s_ {BA} + s_ {AB} = 1 / \ sqrt {c_ {AB} c_ {BA}} \ quad (4)$

La abuela ha llegado

Por fin. Expresión (4): esta es la fórmula deseada.

La distancia entre los vértices de la gráfica de dos nodos es inversamente proporcional a la raíz cuadrada del producto de los contraenlaces.

Puede cargar el libro de texto de la escuela con otra fórmula inútil.

Si las conexiones son iguales, entonces el resultado coincide con la distancia resistiva en los gráficos no dirigidos:

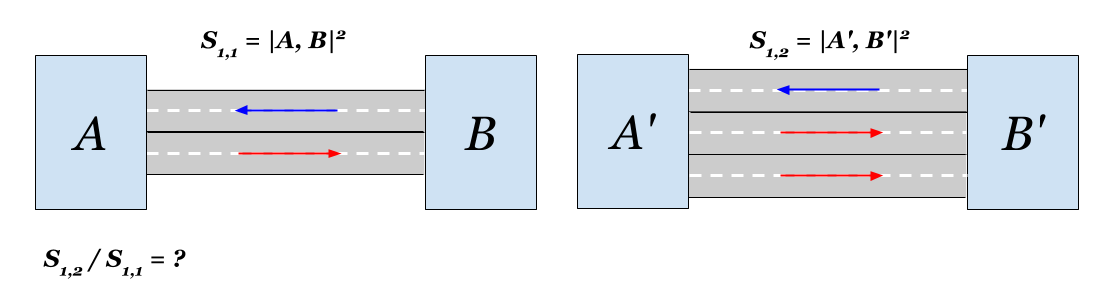
$$$S_ {c, c} (A, B) = 1 / c \ quad (4.1)$

Calcularemos qué hay allí con nuestra ciudad. Si coloca un segundo carril, la comunicación en una dirección se duplicará. En consecuencia, la nueva distancia $$$S_ {1, 2} (A, B)$ se puede expresar en términos del original:

$$$S_ {1, 2} (A, B) = 1 / \ sqrt {2 c_ {AB} c_ {BA}} = 1 / \ sqrt {2} S_ {1, 1} (A, B)$

La distancia entre las áreas disminuirá en $$$\ sqrt {2}$ tiempos Era obvio, ¿verdad?

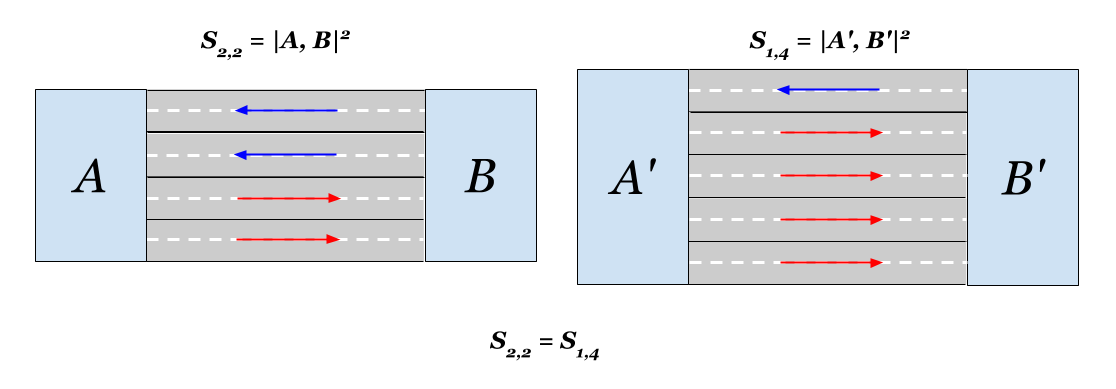
También resulta que, en términos de distancia, agregar un carril a cada carretera de dos carriles en cada lado es equivalente a agregar tres carriles en un lado. La proximidad euclidiana en ambos casos se duplicará. Interesante



Eso es todo. Gracias por su atención