En matemáticas, donde la prueba lo es todo, los hechos también son importantes. Sin embargo, los hechos son buenos, solo mientras el modelo es bueno, y construir modelos es una ocupación poco confiable. Entonces, ¿cuántos hechos serán suficientes?

¿Puedes encontrar el siguiente número en la secuencia?
1, 2, 4, 8
Aquí hay un número más si necesita más datos para tomar una decisión:
1, 2, 4, 8, 16
El siguiente número debería ser 32, ¿verdad? El patrón es claro: para encontrar el siguiente número, debe duplicar el anterior. 1 × 2 = 2; 2 × 2 = 4; 4 × 2 = 8; 8 × 2 = 16. Entonces, el siguiente número debe ser 16 × 2 = 32. ¿Cuántos hechos más se necesitan para confirmar esto?
Pero, aunque es razonable suponer que el siguiente número es 32, esto no siempre será cierto. Considere la siguiente secuencia: contaremos el número de secciones en las que el círculo está dividido por líneas que conectan puntos ubicados en un círculo.
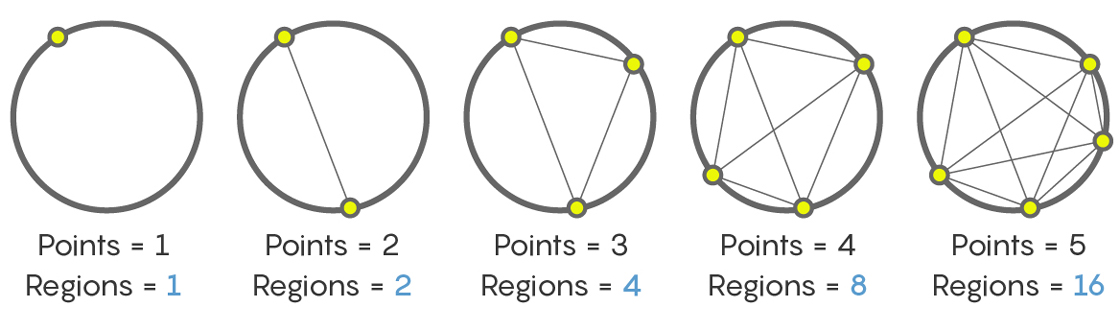
Un punto da una sección (toda la parte interna del círculo). Dos puntos: dos secciones. Tres puntos - cuatro secciones. Cinco y seis son ocho y dieciséis, respectivamente. El resultado es una secuencia.
1, 2, 4, 8, 16
¿Y cuántas secciones aparecerán después de conectar las líneas de seis puntos en el círculo? Nadie lo condenará si, como muchas personas que se enfrentan a esta tarea por primera vez, dice que 32. Pero esto no es así. De hecho, no importa cuán molesto sea, la respuesta será: ¡31! Hágase un recuento y luego verifique nuevamente.
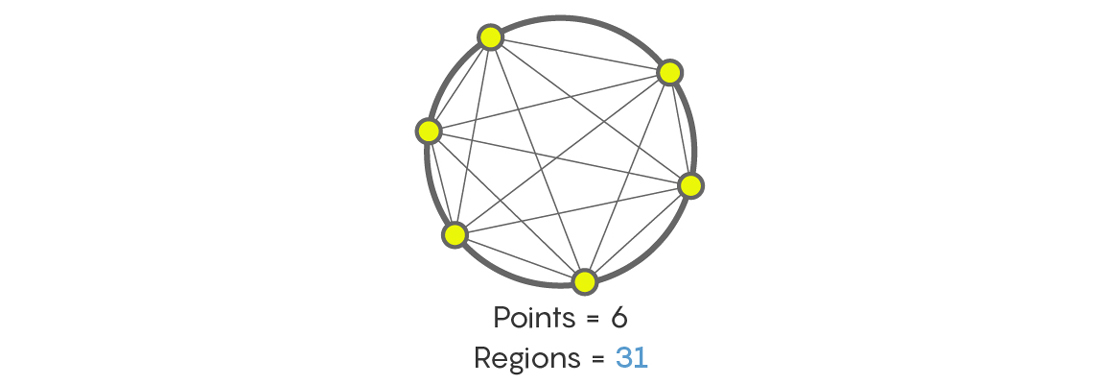
Por supuesto, hay secuencias como 1, 2, 4, 8, 16, 32, 64, etc., de números que se duplican cada vez. Pero hay otras secuencias, por ejemplo, el número máximo de secciones en las que el círculo está dividido por líneas que conectan los puntos en el círculo, y esto es 1, 2, 4, 8, 16, 31, 57, 99, y así sucesivamente. Al cumplir con la secuencia 1, 2, 4, 8, 16, podríamos pensar que todos los hechos son que el siguiente número será 32, pero puede haber algo más.
Las matemáticas tienen una larga tradición de desafiar nuestras expectativas y hacer que nuestra imaginación funcione. Por lo tanto, los matemáticos siempre se esfuerzan por obtener pruebas rigurosas, no solo hechos. La prueba establece la verdad matemática. Todos los hechos pueden señalar 32 como el próximo número en nuestra secuencia, pero sin una prueba rigurosa no podemos estar seguros de eso.
Pero aún así, los hechos para los matemáticos son útiles e importantes. Antes de probar algo, a menudo jugamos con la información disponible, estudiamos el problema, consideramos ejemplos y recopilamos datos. Estudiamos y evaluamos los hechos y decidimos qué hacer a continuación. Estos resultados forman nuestra opinión, proponiendo probar algunos teoremas y refutar otros.
La hipótesis del primo gemelo es un ejemplo en el que los hechos controlan nuestro pensamiento matemático de la misma manera que la prueba. Los primos gemelos son pares de primos que difieren en 2, por ejemplo, 3 y 5, 11 y 13, 101 y 103. La hipótesis de los primos gemelos sugiere que no hay un par más grande de gemelos, es decir, similar Los pares aparecen constantemente en la recta numérica cuando se mueven al infinito.
La hipótesis del primo gemelo no es un teorema, porque, a pesar del hecho de que este es uno de los problemas más famosos en la teoría de números, nadie ha podido demostrarlo. Sin embargo, casi todos creen que es cierto, ya que hay muchos hechos en su apoyo.
Por ejemplo, en nuestra búsqueda de primos constantemente encontramos pares extremadamente grandes de primos gemelos. Cada uno de los números primos del
par más grande
conocido hoy contiene 400,000 dígitos. También se prueban teoremas similares a esta hipótesis. En 2013,
Zhang Ethan sorprendió a la comunidad matemática al demostrar la presencia de un número infinitamente grande de pares de números primos, que no difieren en más de 70 millones. Gracias al proyecto abierto
Polymath que siguió, sabemos que hay un número infinito de pares de primos que difieren en
no más de 246 . Todavía no hemos probado la existencia de un número infinito de pares de números primos que difieren en 2, pero aún así 2 está mucho más cerca de 246 que 246 al infinito.
Por estas y otras razones, la creencia en la justicia, incluso si la hipótesis no está probada, no es muy controvertida. Sin embargo, hay otras áreas de las matemáticas en las que los hechos se utilizan para construir opiniones informadas que resultan ser más controvertidas.
En el estudio de las curvas elípticas, su rango, en términos generales, denota una estimación numérica de la complejidad de resolver esta curva. Durante muchos años se creyó que los
rangos de las curvas elípticas no están limitados , es decir, no hay restricciones en el valor del rango de la curva o en la complejidad de la solución.
Sin embargo, el trabajo reciente hace que los matemáticos piensen en la posibilidad de un rango limitado. El documento proporciona datos que indican que es posible que haya un número finito de curvas cuyo rango es mayor que 21.
Sin embargo, se recomienda precaución. Los hechos recopilados por los matemáticos no están tomados del mundo de las curvas elípticas, sino que se relacionan con las matrices que los investigadores usaron para modelar las curvas. Los modelos matemáticos se usan ampliamente en la ciencia, e incluso se pueden orientar hacia adentro para estudiar las matemáticas en sí. Estas son herramientas increíblemente poderosas que nos permiten reemplazar una tarea incomprensible con una que es más fácil de hacer.
Pero usar modelos es un negocio complicado. Nunca puede estar seguro de que el modelo se comporta de manera bastante similar a lo que estamos tratando de entender, de modo que podamos sacar conclusiones de su comportamiento. Además, uno no puede estar seguro de que nuestro modelo sea similar precisamente en los lugares de mayor importancia. Por lo tanto, es difícil asegurarse de que los hechos que hemos recopilado sobre la base de modelos realmente den testimonio de las propiedades reales de los fenómenos que estamos estudiando. Examinemos estos problemas basados en un modelo simple de una hipótesis simple.
Imagine que queremos estudiar la siguiente afirmación: dos líneas cualquiera son intersectadas o paralelas.
Por intersección entendemos la presencia de líneas rectas en puntos comunes, y por paralelismo el hecho de que van en una dirección pero no se cruzan (este concepto puede definirse de manera diferente, pero lo usaré por simplicidad).
Para estudiar este problema, cree un modelo. Cada línea está representada por la ecuación de la línea oblicua, que puede recordar del curso escolar. Es decir, suponemos que cada línea se puede describir mediante una ecuación de la forma
y = mx + b
donde m es la pendiente de la línea (su inclinación) y b es el punto de intersección del eje y (eje vertical).
Modelar líneas de esta manera es conveniente para experimentar con ellas. El modelo nos permite crear una línea aleatoria seleccionando un par de números aleatorios, myb. Podemos seleccionar un par de líneas aleatorias y verificarlas: ¿se cruzan? ¿Van por un camino? ¿Algo más está sucediendo?
Aquí hay algunos ejemplos de cómo podrían ser los resultados de tales experimentos.
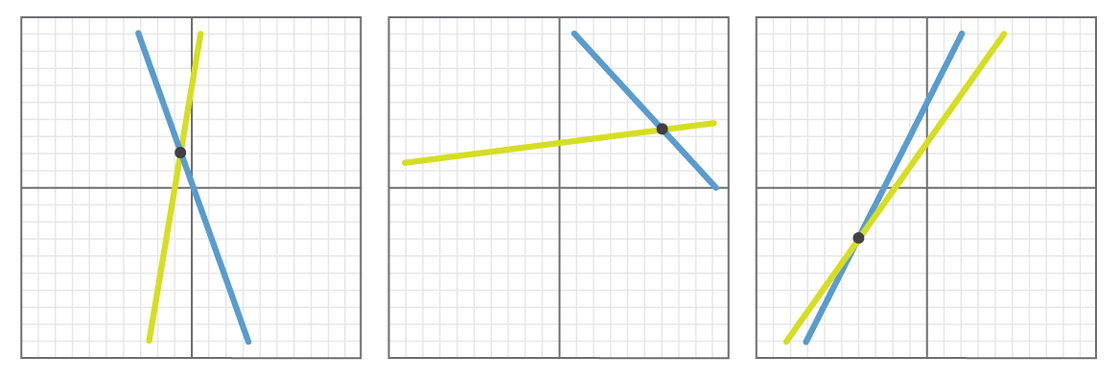
En cada ejemplo, las líneas seleccionadas al azar se cruzan. Si llevamos a cabo este experimento mil veces, o 10,000, o un millón, encontraremos que en todos los casos las líneas se intersectarán o serán paralelas (y muy probablemente, todas las líneas se intersecarán, ya que es poco probable que las dos líneas tengan la misma pendiente, elegida por casualidad).
Por lo tanto, observando un millón de ejemplos, puede llegar a la conclusión de que la hipótesis es muy probable. Todos los hechos respaldan completamente la afirmación de que cualquier par de líneas es paralelo o se cruza.
Sin embargo, los hechos son tan buenos como el modelo es bueno, y el modelado es peligroso. Veamos qué peligros creamos para nosotros en nuestro ejemplo.
Un problema es que ciertos tipos de líneas serán más comunes que otros. Aquí hay un gráfico que muestra 50 líneas con b = 0 y 0 ≤ m ≤ 1.
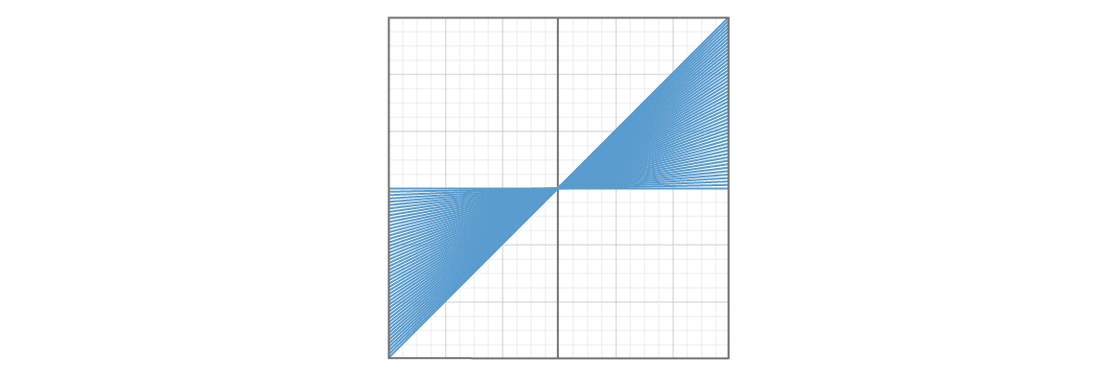
Y aquí hay un gráfico que muestra 50 líneas con b = 0 ym ≥ 1.

Parece que un cuarto del avión está cubierto con líneas rectas con una pendiente de 0 a 1, y otro cuarto está cubierto con líneas rectas con una pendiente mayor que 1. Elegir un número mayor que 1 parece más probable que elegir un número del 0 al 1, por lo que la línea recta es más probable estará en la segunda sección del avión. Esto significa que ciertas líneas, con una pendiente de 0 a 1, estarán extremadamente poco representadas en el modelo. Y si suceden algunas cosas extrañas en esta parte del avión con líneas rectas, es poco probable que nuestro modelo nos cuente sobre esto.
Si observa de cerca el segundo gráfico, veremos otro problema. Cuanto más grande sea m, más pronunciadas serán las líneas rectas. La línea recta más fría es vertical. ¿Cuál es la pendiente de la línea vertical? Por definición, no está definido: no existe un número m que pueda describir la línea vertical. Resulta que no hay una línea vertical en nuestro modelo, y no podemos experimentar con ella. Todavía no hemos comenzado a recopilar datos, pero ya hemos descartado algunos casos especiales simplemente debido al esquema de construcción del modelo.
Lo mismo se refiere al problema más grave de nuestro modelo. Las personas que imaginan fácilmente el espacio tridimensional probablemente notaron de inmediato que nuestra hipótesis es errónea. Una línea recta no tiene que cruzarse ni ser paralela. Imagine dos pasillos que van en diferentes direcciones en diferentes pisos de un edificio. Estas son líneas rectas que se cruzan, líneas rectas que no se cruzan y no son paralelas.
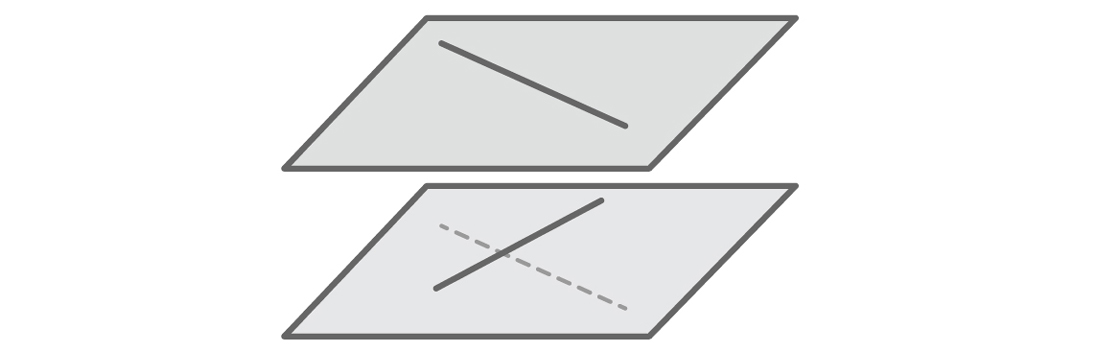
Las líneas cruzadas deben estar en diferentes planos. Pero dado que nuestro modelo define cualquier línea a través de la ecuación y = mx + b, automáticamente imaginamos que todas las líneas están en el mismo plano. Nuestro modelo solo dará hechos que respalden nuestra hipótesis, porque si dos líneas se encuentran en el mismo plano, realmente deben cruzarse o ir paralelas. No veremos otros hechos: no hay líneas de intersección en nuestro modelo. Como en el caso de las líneas verticales, el modelo descartó lo que no podíamos imaginar.
Este es un ejemplo simple que usa un modelo estúpido con un montón de problemas, incluidas preguntas difíciles, como el procedimiento para elegir números aleatorios de conjuntos infinitos. Los matemáticos profesionales que estudian las filas de curvas elípticas nunca habrían cometido errores tan simplificados y obvios.
Estos matemáticos saben qué precauciones deben tomarse al trabajar con modelos. Saben que, independientemente de cuán útil e interesante sea el modelo, o cuán convincentes sean los datos recopilados, las curvas elípticas pueden revelar propiedades que no imaginaron. Y si esto no se puede imaginar, su modelo no lo tendrá en cuenta y, por lo tanto, los hechos no se reflejarán.
Pero ya sea que el nuevo modelo sea correcto o no, obligó a los matemáticos a pensar productivamente sobre las curvas elípticas. Si realmente refleja la verdad, las ideas del mundo de las matrices pueden explicar el comportamiento de las curvas. De lo contrario, comprender por qué las curvas elípticas no pueden modelarse de esta manera puede conducir a una mejor comprensión del problema. Los hechos que recopilamos pueden acercarnos a la prueba, de una forma u otra.