Enlaces rápidos
-
El camino a la versión 12-
Primero, algunas matemáticas-
El cálculo de la incertidumbre-
Matemáticas clásicas, elementales y avanzadas-
Más con polígonos-
Computación con poliedros-
Geometría de estilo euclid hecha computable-
Volviéndose súper simbólico con teorías axiomáticas-
El problema del cuerpo n-
Extensiones de idiomas y conveniencias-
Más superfunciones de aprendizaje automático-
Lo último en redes neuronales-
Computación con imágenes-
Reconocimiento de voz y más con audio-
Procesamiento de lenguaje natural-
Química computacional-
Computación geográfica extendida-
Muchas mejoras de poca visualización-
Ajuste de la integración de la base de conocimiento-
Integración de Big Data desde bases de datos externas-
RDF, SPARQL y todo eso-
Optimización numérica-
Análisis de elementos finitos no lineales-
Compilador nuevo y sofisticado-
Llamar a Python y otros idiomas-
Más para Wolfram "Super Shell"-
Marionetas de un navegador web-
Microcontroladores independientes-
Llamar al lenguaje Wolfram desde Python y otros lugares-
Vinculación al Universo Unitario-
Entornos simulados para el aprendizaje automático-
Computación Blockchain (y CryptoKitty)-
Y cripto ordinario también-
Conexión a feeds de datos financieros-
Ingeniería de software y actualizaciones de plataforma-
Y mucho más ...
16 de abril de 2019 - Stephen Wolfram
Hoy estamos lanzando la versión 12 de
Wolfram Language (y
Mathematica ) en
plataformas de escritorio y en
Wolfram Cloud . Lanzamos la
versión 11.0 en agosto de 2016 ,
11.1 en marzo de 2017 ,
11.2 en septiembre de 2017 y
11.3 en marzo de 2018 . Es un gran salto de la Versión 11.3 a la Versión 12.0. En total, hay
278 funciones completamente nuevas , en quizás 103 áreas, junto con miles de actualizaciones diferentes en todo el sistema:
En una "
versión entera " como 12, nuestro objetivo es proporcionar nuevas áreas de funcionalidad completamente completas. Pero en cada lanzamiento también queremos ofrecer los últimos resultados de nuestros esfuerzos de I + D. En 12.0, quizás la mitad de nuestras nuevas funciones pueden considerarse áreas de acabado que se iniciaron en versiones anteriores ".1", mientras que la mitad comienza nuevas áreas. Discutiré los dos tipos de funciones en esta pieza, pero haré especial hincapié en los detalles de las novedades al pasar de 11.3 a 12.0.
Debo decir que ahora que 12.0 está terminado, estoy sorprendido de cuánto hay en él y cuánto hemos agregado desde 11.3. En mi discurso de apertura en nuestra
Conferencia de Tecnología Wolfram en octubre pasado, resumí lo que teníamos hasta ese momento, e incluso eso tomó casi 4 horas. Ahora hay aún más.
Lo que hemos podido hacer es un testimonio tanto de la fortaleza de nuestro esfuerzo de I + D como de la eficacia del Wolfram Language como entorno de desarrollo. Ambas cosas, por supuesto, se han estado
construyendo durante tres décadas . Pero una cosa nueva con 12.0 es que hemos estado permitiendo que la gente vea nuestro proceso de diseño detrás de escena:
transmisión en vivo de más de 300 horas de mis reuniones de diseño interno . Entonces, además de todo lo demás, sospecho que esto convierte a la Versión 12.0 en la primera versión de software importante en la historia que se ha abierto de esta manera.
Bien, entonces, ¿qué hay de nuevo en 12.0? Hay algunas cosas grandes y sorprendentes, especialmente en
química ,
geometría ,
incertidumbre numérica e
integración de bases de datos . Pero en general, hay muchas cosas en muchas áreas, y de hecho, incluso el resumen básico de ellas en el
Centro de Documentación ya tiene 19 páginas:
Aunque hoy en día la gran mayoría de lo que hace Wolfram Language (y Mathematica) no es lo que generalmente se considera matemático, aún ponemos un esfuerzo inmenso en I + D para ampliar las fronteras de lo que se puede hacer en matemáticas. Y como primer ejemplo de lo que hemos agregado en 12.0, aquí está el
ComplexPlot3D bastante colorido:
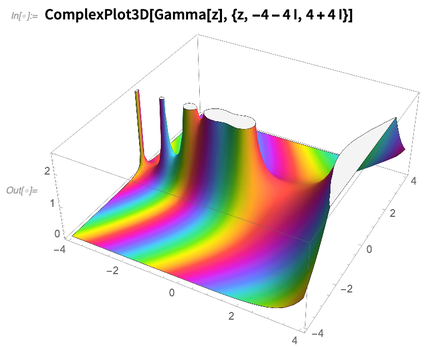
Siempre ha sido posible escribir el código de Wolfram Language para hacer trazados en el plano complejo. Pero solo ahora hemos resuelto los problemas matemáticos y de algoritmos necesarios para automatizar el proceso de trazar de manera robusta incluso funciones bastante patológicas en el plano complejo.
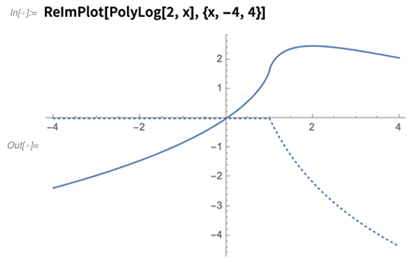
Hace años, recuerdo
trazar minuciosamente la
función dilogaritmo , con sus partes reales e imaginarias. Ahora
ReImPlot simplemente lo hace:
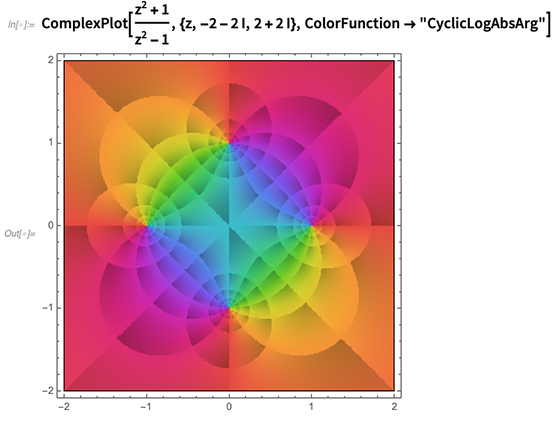
La visualización de funciones complejas es (juego de palabras aparte) una historia compleja, con detalles que hacen una gran diferencia en lo que uno nota sobre una función. Por lo tanto, una de las cosas que hemos hecho en 12.0 es introducir formas estandarizadas cuidadosamente seleccionadas (como
funciones de color con nombre) para resaltar diferentes características:
El cálculo de la incertidumbre
Las mediciones en el mundo real a menudo tienen incertidumbre que se representa como valores con ± errores. Hemos tenido paquetes adicionales para manejar "números con errores" por edades. Pero en la Versión 12.0 estamos construyendo computación con incertidumbre, y lo estamos haciendo bien.
La clave es el objeto simbólico
Alrededor de [
x, δ ], que representa un valor "alrededor de
x ", con incertidumbre
δ :
Puedes hacer aritmética con
Around , y hay un cálculo completo de cómo se combinan las incertidumbres:
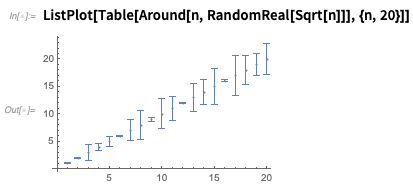
Si traza los números
Alrededor , se mostrarán con barras de error:
Hay muchas opciones, como aquí hay una forma de mostrar incertidumbre tanto en
x como en
y :
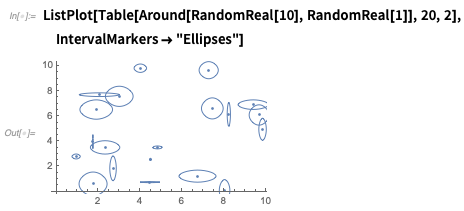
Puede tener
alrededor de cantidades:
Y también puede tener objetos simbólicos
Alrededor :
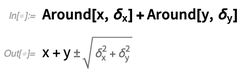
Pero, ¿qué es realmente un objeto
Alrededor ? Es algo donde hay ciertas reglas para combinar incertidumbres, que se basan en distribuciones normales no correlacionadas. Pero no se hace ninguna declaración de que
Alrededor de [
x, δ ] represente cualquier cosa que realmente en detalle siga una distribución normal, al
igual que
Alrededor de [
x, δ ] representa un número específicamente en el intervalo definido por el
Intervalo [{
x - δ, x + δ }]. Es solo que los objetos
Alrededor propagan sus errores o incertidumbres de acuerdo con reglas generales consistentes que capturan con éxito lo que generalmente se hace en la ciencia experimental.
OK, entonces digamos que haces un montón de medidas de algún valor. Puede obtener una estimación del valor, junto con su incertidumbre, utilizando
MeanAround (y, sí, si las mediciones mismas tienen incertidumbres, se tendrán en cuenta al ponderar sus contribuciones):
Las funciones en todo el sistema, especialmente en
el aprendizaje automático, comienzan a tener la opción
ComputeUncertainty ->
True , lo que les hace dar objetos
Alrededor en lugar de números puros.
Alrededor puede parecer un concepto simple, pero está lleno de sutilezas, que es la razón principal por la que se ha tomado hasta ahora para que ingrese al sistema. Muchas de las sutilezas giran en torno a las correlaciones entre incertidumbres. La idea básica es que se supone que la incertidumbre de cada objeto
Around es independiente. Pero a veces uno tiene valores con incertidumbres correlacionadas, por lo que, además de
Around , también está
VectorAround , que representa un vector de valores potencialmente correlacionados con una matriz de covarianza específica.
Hay incluso más sutileza cuando se trata de cosas como fórmulas algebraicas. Si uno reemplaza x aquí con un
Around , entonces, siguiendo las reglas de
Around , se supone que cada instancia no está correlacionada:
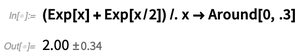
Pero probablemente uno quiera suponer aquí que aunque el valor de x puede ser incierto, será el mismo para cada instancia, y uno puede hacer esto usando la función
AroundReplace (observe que el resultado es diferente):
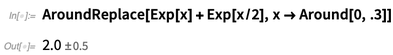
Hay mucha sutileza en cómo mostrar números inciertos. Como cuántos ceros finales deberías poner:
O cuánta precisión de la incertidumbre debe incluir (hay un punto de corte convencional cuando los dígitos finales son 35):
En casos raros donde se conocen muchos dígitos (piense, por ejemplo, algunas
constantes físicas ), uno quiere ir a una forma diferente para especificar la incertidumbre:
Y sigue y sigue. Pero gradualmente,
Around comenzará a aparecer en todo el sistema. Por cierto, hay muchas otras formas de especificar los números
Alrededor . Este es un número con un 10% de error relativo:
Esto es lo mejor que
Around puede hacer para representar un intervalo:
Para una
distribución ,
Around calcula la varianza:
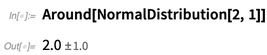
También puede tener en cuenta la asimetría al dar incertidumbres asimétricas:
Matemáticas Clásicas, Elementales y Avanzadas
Al hacer que las matemáticas sean computacionales, siempre es un desafío poder "hacer todo bien" y no confundir o intimidar a los usuarios de primaria. La versión 12.0 presenta varias cosas para ayudar. Primero, intente resolver una
ecuación quíntica irreducible:
En el pasado, esto habría mostrado un montón de objetos
raíz explícitos. Pero ahora los objetos
raíz están formateados como cuadros que muestran sus valores numéricos aproximados. Los cálculos funcionan exactamente igual, pero la pantalla no confronta inmediatamente a las personas con tener que saber sobre números algebraicos.
Cuando decimos
Integrar , queremos decir "encontrar una integral", en el sentido de una antiderivada. Pero en el cálculo elemental, las personas quieren ver constantes explícitas de integración (como siempre lo han hecho en
Wolfram | Alpha ), por lo que agregamos
una opción para eso (y C [
n ] también tiene una nueva y agradable forma de salida):
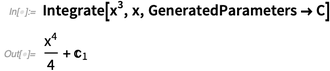
Cuando comparamos nuestras capacidades de integración simbólica, lo hacemos realmente bien. Pero siempre se puede hacer más, particularmente en términos de encontrar las formas más simples de integrales (y a nivel teórico, esto es una consecuencia inevitable de la indecidibilidad de la equivalencia de expresión simbólica). En la versión 12.0, hemos seguido recogiendo en la frontera, agregando casos como:
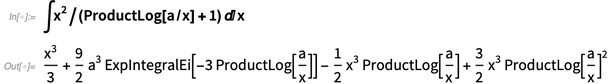
En la versión 11.3 presentamos el análisis asintótico, pudiendo encontrar valores asintóticos de integrales, etc. La versión 12.0 agrega sumas asintóticas, recurrencias asintóticas y soluciones asintóticas a las ecuaciones:
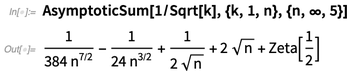
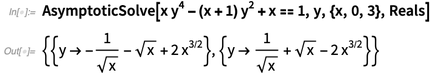
Una de las mejores cosas de hacer cálculos matemáticos es que nos brinda nuevas formas de explicar las matemáticas en sí. Y algo que hemos estado haciendo es mejorar nuestra documentación para que explique las matemáticas y las funciones. Por ejemplo, aquí está el comienzo de la documentación sobre
Límite , con diagramas y ejemplos de las principales ideas matemáticas:
Los polígonos han sido parte del Wolfram Language desde la Versión 1. Pero en la Versión 12.0 se están generalizando: ahora hay una forma sistemática de especificar agujeros en ellos. Un caso de uso geográfico clásico es el polígono para
Sudáfrica, con su agujero para el país de
Lesotho .
En la versión 12.0, al igual que
Root ,
Polygon obtiene una nueva forma conveniente de visualización:
Puede calcular con él como antes:
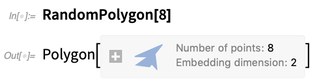
RandomPolygon también es nuevo. Puede pedir, digamos, 5 polígonos convexos aleatorios, cada uno con 10 vértices, en 3D:
Hay muchas operaciones nuevas en polígonos. Como
PolygonDecomposition , que puede, por ejemplo, descomponer un polígono en partes convexas:
Los polígonos con agujeros también introducen la necesidad de otros tipos de operaciones, como
OuterPolygon ,
SimplePolygonQ y
CanonicalizePolygon .
Los polígonos son bastante sencillos de especificar: solo da sus vértices en orden (y si tienen agujeros, también da los vértices de los agujeros). Los poliedros son un poco más complicados: además de dar los vértices, tienes que decir cómo estos vértices forman caras. Pero en la Versión 12.0,
Polyhedron le permite hacer esto en considerable generalidad, incluidos los huecos (el análogo 3D de agujeros), etc.
Pero primero, reconociendo sus más de
2000 años de historia , la Versión 12.0 introduce funciones para los cinco
sólidos platónicos :
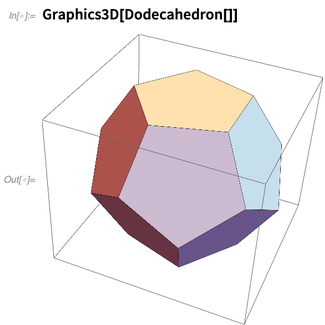
Y dados los sólidos platónicos, uno puede comenzar a computar inmediatamente con ellos:
Aquí está el ángulo sólido subtendido en el vértice 1 (ya que es platónico, todos los vértices dan el mismo ángulo):
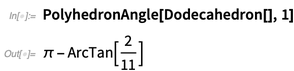
Aquí hay una operación realizada en el poliedro:
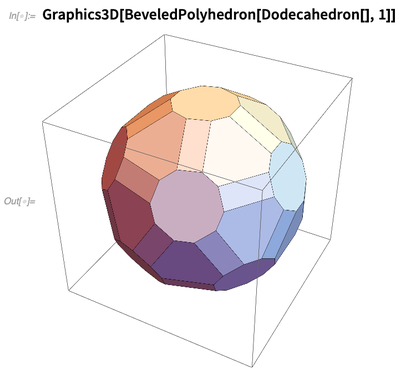
Más allá de los sólidos platónicos, la Versión 12 también incorpora todos los "
poliedros uniformes " (
n bordes
ym caras se encuentran en cada vértice), y también puede obtener versiones simbólicas de poliedros de poliedros con nombre de
PolyhedronData :
Puede hacer cualquier poliedro (incluido uno "aleatorio", con
RandomPolyhedron ) y luego hacer los cálculos que desee en él:
Mathematica y Wolfram Language son muy poderosos para hacer
geometría computacional explícita y
geometría representada en términos de álgebra . Pero, ¿qué pasa con la geometría de la forma en que se hace en
los Elementos de Euclides, en el cual uno hace afirmaciones geométricas y luego ve cuáles son sus consecuencias?
Bueno, en la Versión 12, con toda la torre de tecnología que hemos construido, finalmente podemos ofrecer un nuevo estilo de cálculo matemático, que en efecto automatiza lo que Euclid estaba haciendo hace más de 2000 años. Una idea clave es introducir "escenas geométricas" simbólicas que tienen símbolos que representan construcciones como puntos, y luego definir objetos geométricos y relaciones en términos de ellos.
Por ejemplo, aquí hay una escena geométrica que representa un triángulo
a, b, c y un círculo a través de
a, byc , con el centro
o , con la restricción de que
o está en el punto medio de la línea de
a a
c :
Por sí solo, esto es solo una cosa simbólica. Pero podemos hacer operaciones al respecto. Por ejemplo, podemos pedir una instancia aleatoria de la misma, en la que
a, b, c y
o se especifiquen:
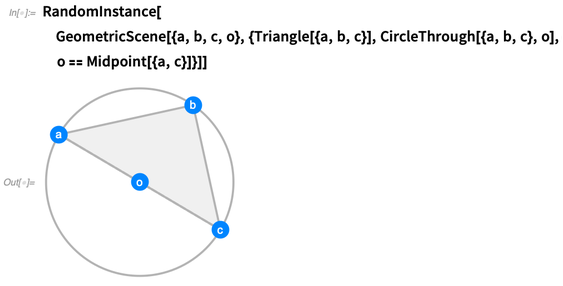
Puede generar tantas instancias aleatorias como desee. Intentamos que las instancias sean lo más genéricas posible, sin coincidencias que no estén forzadas por las restricciones:
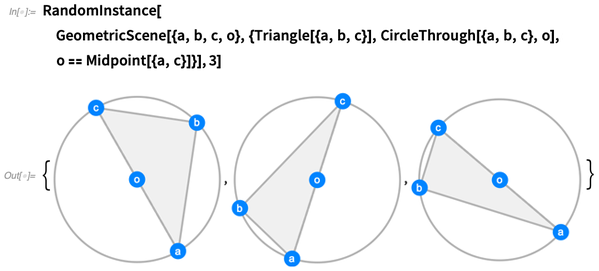
Bien, pero ahora "juguemos Euclides" y encontremos conjeturas geométricas que sean consistentes con nuestra configuración:
Para una escena geométrica dada, puede haber muchas conjeturas posibles. Intentamos elegir los interesantes. En este caso llegamos a dos, y lo que se ilustra es el primero: que la línea ba es perpendicular a la línea cb. Como sucede, este resultado aparece en Euclides (está en el
Libro 3, como parte de la Proposición 31 ), aunque generalmente se llama
el teorema de Thales .
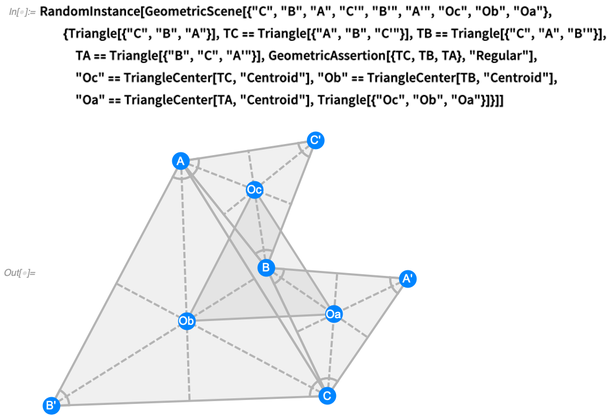
En 12.0, ahora tenemos un lenguaje simbólico completo para representar cosas típicas que aparecen en la geometría de estilo Euclides. Aquí hay una situación más compleja, correspondiente a lo que se llama
el teorema de Napoleón :
En 12.0 hay muchas funciones geométricas nuevas y útiles que funcionan en coordenadas explícitas:
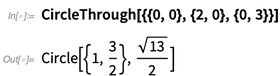
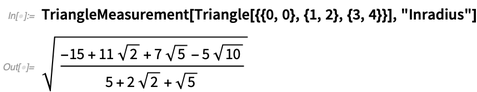
Para los triángulos hay 12 tipos de "centros" compatibles y, sí, puede haber coordenadas simbólicas:
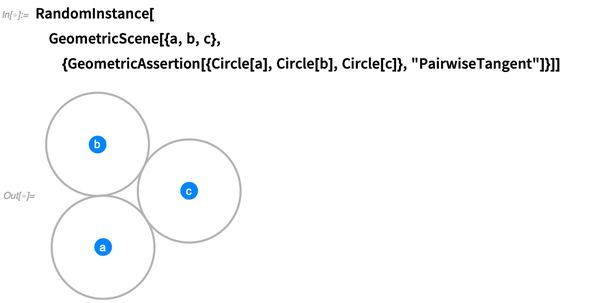
Y para apoyar la configuración de enunciados geométricos también necesitamos "
aserciones geométricas ". En 12.0 hay 29 tipos diferentes, como
"Paralelo" ,
"Congruente" ,
"Tangente" ,
"Convexo" , etc. Aquí hay tres círculos que se afirma que son tangentes por pares:
Yendo súper simbólico con teorías axiomáticas
La versión 11.3 introdujo
FindEquationalProof para generar representaciones simbólicas de pruebas. Pero, ¿qué axiomas deberían usarse para estas pruebas? La versión 12.0 presenta
AxiomaticTheory , que proporciona axiomas para varias
teorías axiomáticas comunes.
Aquí está mi
sistema de axiomas favorito :
¿Qué significa esto? En cierto sentido, es una expresión simbólica más simbólica de lo que estamos acostumbrados. En algo como 1 +
x no decimos cuál es el valor de
x , pero imaginamos que puede tener un valor. En la expresión anterior, a, byc son puros "símbolos formales" que cumplen una función esencialmente estructural, y nunca se puede considerar que tengan valores concretos.
¿Qué pasa con el · (punto central)? En 1 +
x sabemos lo que significa +. Pero el · pretende ser un operador puramente abstracto. El punto del axioma está en efecto para
definir una restricción sobre lo que puede representar. En este caso particular, resulta que el axioma es un
axioma para el álgebra booleana , por lo que puede representar a
Nand y
Nor . Pero podemos derivar las consecuencias del axioma de manera completamente formal, por ejemplo con
FindEquationalProof :
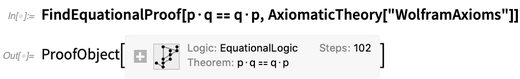
Hay bastante sutileza en todo esto. En el ejemplo anterior, es útil tener · como operador, sobre todo porque se muestra muy bien. Pero no tiene un significado incorporado, y
AxiomaticTheory le permite dar algo más (aquí
f ) como operador:
¿Qué hace el
"Nand" allí? Es un nombre para el operador (pero no debe interpretarse como algo relacionado con el valor del operador). En los
axiomas para la teoría de grupos , por ejemplo, aparecen varios operadores:
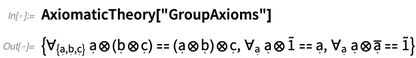
Esto proporciona las representaciones predeterminadas de los distintos operadores aquí:
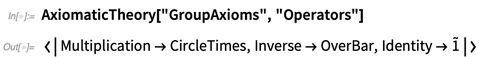AxiomaticTheory sabe sobre teoremas notables para sistemas axiomáticos particulares:
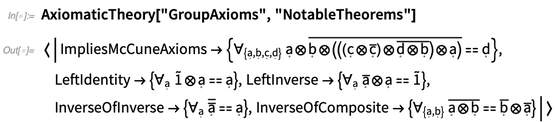
La idea básica de los símbolos formales se introdujo en la Versión 7, para hacer cosas como representar variables ficticias en construcciones generadas como estas:
Puede ingresar un símbolo formal usando
\ [FormalA] o Esc, a, Esc, etc. Pero en la versión 7,
\ [FormalA] se
procesó como
a . Y eso significaba que la expresión anterior se veía así:
Siempre pensé que esto parecía increíblemente complicado. Y para la Versión 12, queríamos simplificarlo. Probamos muchas posibilidades, pero finalmente nos decidimos por puntos grises únicos, que creo que se ven mucho mejor.
En
AxiomaticTheory , tanto las variables como los operadores son "puramente simbólicos". Pero una cosa que es definitiva es la aridad de cada operador, que se puede preguntar
AxiomaticTheory :
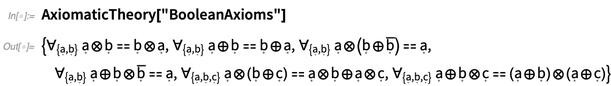
Convenientemente, la representación de operadores y aridades se puede alimentar inmediatamente a
Agrupaciones , para obtener posibles expresiones que involucren variables particulares:
El problema del cuerpo n
Las teorías axiomáticas representan un área histórica clásica para las matemáticas. Otra área histórica clásica, mucho más en el lado aplicado, es el
problema de los
n cuerpos . La versión 12.0 presenta
NBodySimulation , que ofrece simulaciones del problema de n cuerpos. Aquí hay un problema de tres cuerpos (piense en la
Tierra, la Luna y el Sol ) con ciertas condiciones iniciales (y la ley de la fuerza del cuadrado inverso):
Puede preguntar sobre varios aspectos de la solución; esto traza las posiciones en función del tiempo:
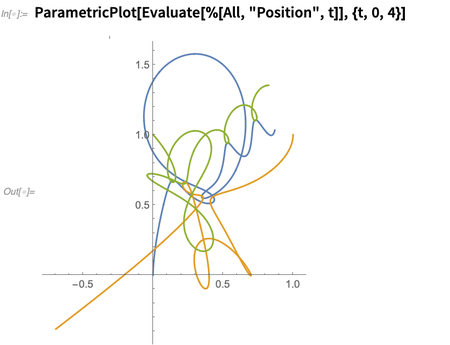
Debajo, esto es solo resolver ecuaciones diferenciales, pero, un poco como
SystemModel ,
NBodySimulation proporciona una forma conveniente de configurar las ecuaciones y manejar sus soluciones. Y sí, las leyes de fuerza estándar están incorporadas, pero puedes definir las tuyas.
Extensiones de idiomas y conveniencias
Hemos estado puliendo el núcleo del Wolfram Language durante más de 30 años, y en cada versión sucesiva terminamos introduciendo algunas nuevas extensiones y comodidades.
Hemos tenido la función
Información desde la Versión 1.0, pero en 12.0 la hemos ampliado enormemente. Solía dar información sobre los símbolos (aunque también se ha modernizado):
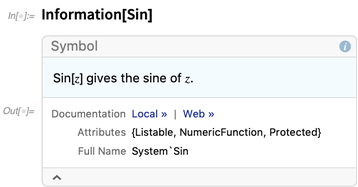
Pero ahora también proporciona información sobre muchos tipos de objetos. Aquí hay información sobre un clasificador:
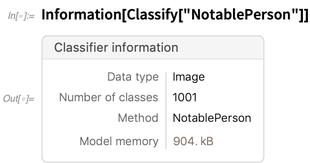
Aquí hay información sobre un objeto en la nube:
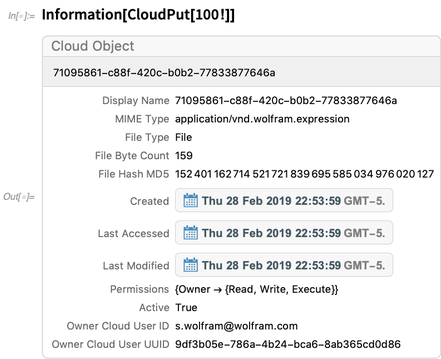
Desplácese sobre las etiquetas en el "cuadro de información" y podrá encontrar los nombres de las propiedades correspondientes:
Para las entidades, la
información proporciona un resumen de los valores de propiedad conocidos:
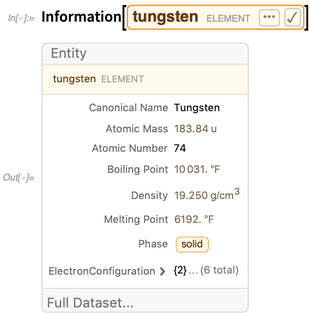
En las últimas versiones, hemos introducido muchos nuevos formularios de visualización de resumen. En la versión 11.3 presentamos
Iconize , que es esencialmente una forma de crear un formulario de visualización de resumen para cualquier cosa. Iconize ha demostrado ser aún más útil de lo que anticipamos originalmente. Es ideal para ocultar una complejidad innecesaria tanto en las libretas como en partes del código Wolfram Language. En 12.0 hemos rediseñado la forma en que Iconize muestra, particularmente para que se "lea bien" dentro de las expresiones y el código.
Puede iconizar explícitamente algo:
Presione el + y verá algunos detalles:
Prensa
y obtendrás la expresión original nuevamente:
Si tiene muchos datos a los que desea hacer referencia en un cálculo, siempre puede almacenarlos en un archivo o en la
nube (o incluso en un
repositorio de datos ). Sin embargo, generalmente es más conveniente simplemente ponerlo en su computadora portátil, para que tenga todo en el mismo lugar. Una forma de evitar que los datos "se apoderen de su computadora portátil" es
colocar celdas cerradas . Pero Iconize ofrece una forma mucho más flexible y elegante de hacerlo.
Cuando escribes código, a menudo es conveniente "iconizar en el lugar". El menú del botón derecho ahora le permite hacer eso:
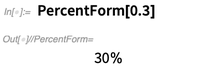
Hablando de visualización, aquí hay algo pequeño pero conveniente que agregamos en 12.0:
Y aquí hay un par de otras "conveniencias numéricas" que agregamos:
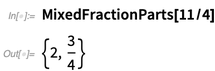
La programación funcional siempre ha sido una parte central del Wolfram Language. Pero continuamente buscamos extenderlo e introducir nuevas primitivas generalmente útiles. Un ejemplo en la versión 12.0 es
SubsetMap :
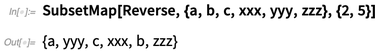
Las funciones son normalmente cosas que pueden tomar varias entradas, pero siempre dan una sola pieza de salida. Sin embargo, en áreas como
la computación cuántica , uno está interesado en tener
n entradas y
n salidas.
SubsetMap implementa eficazmente
n-> n funciones, recogiendo entradas de
n posiciones especificadas en una lista, aplicando alguna operación a ellas y luego volviendo a colocar los resultados en las mismas
n posiciones.
Comencé a formular lo que ahora es
SubsetMap hace aproximadamente un año. Y rápidamente me di cuenta de que en realidad podría haber usado esta función en todo tipo de lugares a lo largo de los años. Pero, ¿cómo debería llamarse este particular "bulto de trabajo computacional"? Mi nombre de trabajo inicial fue
ArrayReplaceFunction (que acorté a
ARF en mis notas). En una
secuencia de reuniones (livestreamed) fuimos y salimos. Hubo ideas como
ApplyAt (pero en realidad no es
Apply ) y
MutateAt (pero no está haciendo mutación en el sentido del valor), así como
RewriteAt ,
Reemplazar ,
MultipartApply y
ConstructInPlace . Hubo ideas sobre formas
curriculares de "decorador de funciones", como
PartAppliedFunction ,
PartwiseFunction ,
AppliedOnto ,
AppliedAcross y
MultipartCurry .
Pero de alguna manera, cuando explicamos la función, volvimos a hablar sobre cómo funcionaba en un subconjunto de una lista y cómo era realmente como
Mapa , excepto que estaba operando en múltiples elementos a la vez. Así que finalmente nos decidimos por el nombre
SubsetMap . Y, en otro refuerzo de la importancia del diseño del lenguaje, es notable cómo, una vez que uno tiene un nombre para algo como esto, inmediatamente puede razonar sobre ello y ver dónde se puede usar.
Durante muchos años hemos trabajado arduamente para que Wolfram Language sea el sistema de más alto nivel y más automatizado para realizar
aprendizaje automático de última generación . Al principio, presentamos las "superfunciones"
Clasificar y predecir que realizan tareas de
clasificación y predicción de forma completamente automatizada, eligiendo automáticamente el mejor enfoque para la entrada particular dada. En el camino, hemos introducido otras superfunciones, como
SequencePredict ,
ActiveClassification y
FeatureExtract .
En la versión 12.0 tenemos varias superfunciones importantes nuevas de aprendizaje automático. Hay
FindAnomalies , que encuentra "elementos anómalos" en los datos:
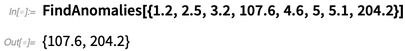
Junto con esto, está
DeleteAnomalies , que elimina elementos que considera anómalos:
También hay
SynthesizeMissingValues , que intenta generar valores plausibles para datos faltantes:
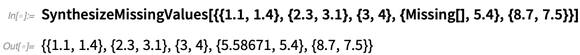
¿Cómo funcionan estas funciones? Todos se basan en una nueva función llamada
LearnDistribution , que trata de aprender la distribución subyacente de datos, dado un cierto conjunto de ejemplos. Si los ejemplos fueran solo números, esto sería esencialmente un problema estadístico estándar, para lo cual podríamos usar algo como
EstimatedDistribution . Pero el punto sobre
LearnDistribution es que funciona con datos de cualquier tipo, no solo números. Aquí está aprendiendo una distribución subyacente para una colección de colores:
Una vez que tenemos esta "distribución aprendida", podemos hacer todo tipo de cosas con ella. Por ejemplo, esto genera 20 muestras aleatorias a partir de él:
Pero ahora piense en
FindAnomalies . Lo que tiene que hacer es descubrir qué puntos de datos son anómalos en relación con lo que se espera. O, en otras palabras, dada la distribución subyacente de los datos, encuentra qué puntos de datos son atípicos, en el sentido de que deberían ocurrir solo con una probabilidad muy baja de acuerdo con la distribución.
Y al igual que para una distribución numérica ordinaria, podemos calcular el
PDF para un dato en particular. El púrpura es muy probable dada la distribución de colores que hemos aprendido de nuestros ejemplos:
Pero el rojo es realmente muy poco probable:
Para distribuciones numéricas ordinarias, hay conceptos como
CDF que nos dicen probabilidades acumulativas, digamos que obtendremos resultados que están "más lejos" que un valor particular. Para espacios de cosas arbitrarias, no existe realmente una noción de "más allá". Pero se nos ocurrió una función que llamamos
RarerProbability , que nos dice cuál es la probabilidad total de generar un ejemplo con un PDF más pequeño que el que damos:
Ahora tenemos una forma de describir anomalías: son solo puntos de datos que tienen una probabilidad muy rara. Y, de hecho,
FindAnomalies tiene una opción
AcceptanceThreshold (con el valor predeterminado 0.001) que especifica lo que debe contar como "muy pequeño".
Bien, pero veamos cómo funciona esto en algo más complicado que los colores. Vamos a entrenar un detector de anomalías observando 1000 ejemplos de dígitos escritos a mano:
Ahora
FindAnomalies puede decirnos qué ejemplos son anómalos:
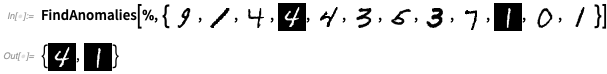
Primero presentamos nuestro marco simbólico para construir, explorar y usar redes neuronales en 2016, como parte de la Versión 11. Y en todas las versiones desde entonces, hemos agregado todo tipo de características de vanguardia. En junio de 2018, presentamos nuestro
repositorio de redes neuronales para facilitar el acceso a los últimos modelos de redes neuronales desde Wolfram Language, y ya hay casi 100 modelos seleccionados de muchos tipos diferentes en el repositorio, y se agregan nuevos constantemente.
Entonces, si necesita la última
red neuronal "transformador" BERT (que se agregó hoy), puede obtenerla de
NetModel :
Puede abrir esto y ver la red que está involucrada (y, sí, hemos actualizado la visualización de gráficos de red para la Versión 12.0):
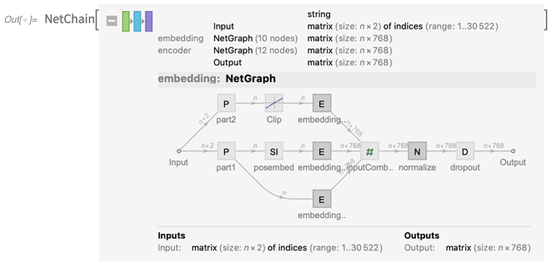
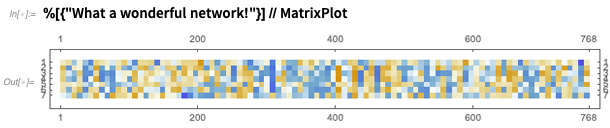
Y puede usar inmediatamente la red, aquí para producir algún tipo de matriz de "características de significado":
En la versión 12.0 hemos introducido varios tipos de capas nuevas, en particular
AttentionLayer , que permite configurar las últimas arquitecturas de "transformador", y hemos mejorado nuestras capacidades de "programación funcional de red neuronal", con elementos como
NetMapThreadOperator y secuencia múltiple
NetFoldOperator . Además de estas mejoras "dentro de la red", la Versión 12.0 agrega todo tipo de nuevos casos de
NetEncoder y
NetDecoder , como la
tokenización de BPE para texto en cientos de idiomas, y la capacidad de incluir funciones personalizadas para ingresar y salir de datos redes neuronales
Pero algunas de las mejoras más importantes en la Versión 12.0 son más infraestructurales.
NetTrain ahora es compatible
con la capacitación de múltiples GPU , así como también con aritmética de precisión mixta y criterios flexibles de detención temprana. Continuamos utilizando el popular marco de red neuronal de bajo nivel
MXNet (del cual hemos sido los
principales contribuyentes ), para poder aprovechar las últimas optimizaciones de hardware. Hay
nuevas opciones para ver lo que sucede durante el entrenamiento, y también hay
NetMeasurements que le permite realizar 33 tipos diferentes de mediciones sobre el rendimiento de una red:
Las redes neuronales no son la única, o incluso la mejor, forma de hacer aprendizaje automático. Pero una cosa nueva en la Versión 12.0 es que ahora podemos usar
redes de normalización automática en
Clasificar y
Predecir , para que puedan
aprovechar fácilmente
las redes neuronales cuando tenga sentido.
Presentamos
ImageIdentify , para identificar de qué es una imagen, en la Versión 10.1. En la Versión 12.0 hemos logrado generalizar esto, para descubrir no solo de qué es una imagen, sino también qué hay en una imagen. Entonces, por ejemplo,
ImageCases nos mostrará casos de tipos conocidos de objetos en una imagen:
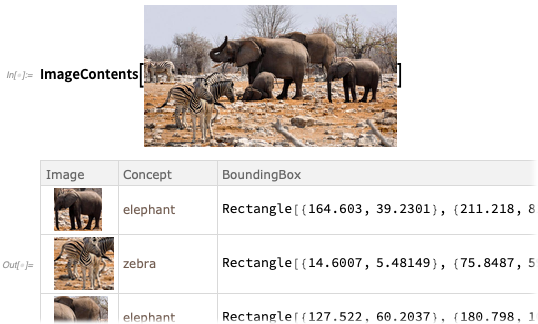
Para más detalles,
ImageContents ofrece un conjunto de datos sobre lo que hay en una imagen:
Puede decirle a
ImageCases que busque un tipo particular de cosas:
Y también puede probar para ver si una imagen contiene un tipo particular de cosas:
En cierto sentido,
ImageCases es como una versión generalizada de
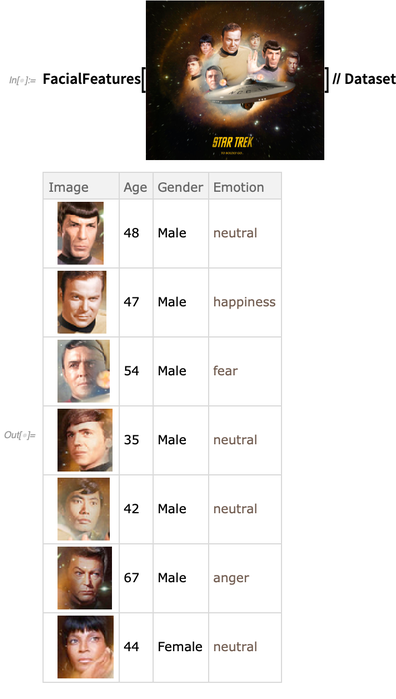
FindFaces , para encontrar rostros humanos en una imagen. Algo nuevo en la Versión 12.0 es que
FindFaces y
FacialFeatures se han vuelto
más eficientes y robustos, con
FindFaces ahora basado en redes neuronales en lugar de procesamiento de imágenes clásico, y la red para
FacialFeatures ahora es de 10 MB en lugar de 500 MB:
Funciones como
ImageCases representan el procesamiento de imágenes de "estilo nuevo", de un tipo que no parecía concebible hace solo unos años. Pero aunque tales funciones le permiten a uno hacer todo tipo de cosas nuevas, todavía hay mucho valor en las técnicas más clásicas. Hemos tenido
un procesamiento de imágenes clásico bastante completo en Wolfram Language durante mucho tiempo, pero seguimos haciendo mejoras incrementales.
Un ejemplo en la Versión 12.0 es el marco de
ImagePyramid , para hacer el procesamiento de imágenes multiescala:
Hay varias funciones nuevas en la Versión 12.0 relacionadas con el cálculo del color. Una idea clave es
ColorsNear , que representa un vecindario en el espacio de color perceptivo, aquí alrededor del color
Rosa :
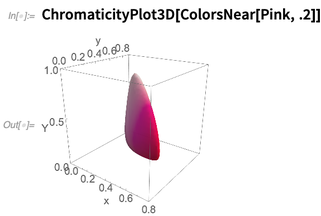
La noción de vecindades de color se puede utilizar, por ejemplo, en la nueva función
ImageRecolor :
Mientras me siento en mi computadora escribiendo esto, le diré algo a mi computadora y lo
capturaré :
Aquí hay un espectrograma del audio que capturé:
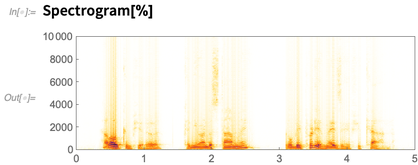
Hasta ahora podríamos hacer esto en la Versión 11.3 (aunque
Spectrogram se volvió 10 veces más rápido en 12.0). Pero ahora aquí hay algo nuevo:
Estamos haciendo voz a texto! Estamos utilizando tecnología de redes neuronales de última generación, pero estoy sorprendido de lo bien que funciona. Está bastante optimizado y somos perfectamente capaces de manejar incluso piezas de audio muy largas, digamos almacenadas en archivos. Y en una computadora típica, la transcripción se ejecutará aproximadamente a la velocidad real en tiempo real, por lo que una hora de discurso tardará aproximadamente una hora en transcribirse.
En este momento consideramos que
Speech Recognize es experimental, y continuaremos mejorando. Pero es interesante ver que otra tarea computacional importante se convierta en una sola función en Wolfram Language.
En la versión 12.0, también hay otras mejoras.
SpeechSynthesize admite nuevos idiomas y nuevas voces (según lo enumerado por
VoiceStyleData []).
Ahora hay
WebAudioSearch, análogo a
WebImageSearch , que le permite buscar audio en la web:
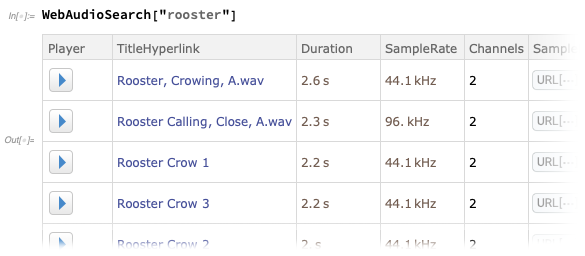
Puede recuperar objetos de
audio reales:
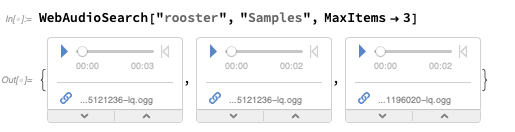
Luego puede hacer espectrogramas u otras medidas:
Y luego, nuevo en la Versión 12.0, puede usar
AudioIdentify para tratar de identificar la categoría de sonido (¿es un gallo parlante?):
Todavía consideramos
AudioIdentify experimental. Es un comienzo interesante, pero definitivamente no funciona, por ejemplo, tan bien como
ImageIdentify .
Una función de audio más exitosa es
PitchRecognize , que trata de reconocer la frecuencia dominante en una señal de audio (utiliza métodos de redes neuronales y "clásicas"). Todavía no puede tratar con "acordes", pero funciona bastante perfectamente para "notas individuales".
Cuando se trata de audio, a menudo se quiere no solo identificar lo que hay en el audio, sino también anotarlo. La versión 12.0 introduce el comienzo de un
marco de audio a gran escala. En este momento,
AudioAnnotate puede marcar dónde hay silencio o dónde hay algo ruidoso. En el futuro, agregaremos identificación del hablante y límites de palabras, y mucho más. Y para seguir con esto, también tenemos funciones como
AudioAnnotationLookup , para seleccionar partes de un objeto de audio que se han anotado de maneras particulares.
Debajo de toda esta funcionalidad de audio de alto nivel hay toda una infraestructura de procesamiento de audio de bajo nivel. La versión 12.0 mejora enormemente
AudioBlockMap (para aplicar filtros a las señales de audio), así como también presenta funciones como
ShortTimeFourier .
Un espectrograma se puede ver un poco como un análogo continuo de una partitura musical, en el que los tonos se trazan en función del tiempo. En la versión 12.0 ahora hay
InverseSpectrogram, que va desde una matriz de datos de espectrograma hasta audio. Desde la versión 2 en 1991, hemos tenido
Play para generar sonido a partir de una función (como
Sin [100 t]). Ahora con el
espectrograma inverso tenemos una manera de pasar de un "mapa de bits de frecuencia-tiempo" a un sonido. (Y sí, hay problemas difíciles sobre las mejores conjeturas para las fases cuando uno solo tiene información de magnitud).
Comenzando con
Wolfram | Alpha , hemos tenido
capacidades de comprensión del lenguaje natural (NLU) excepcionalmente fuertes durante mucho tiempo. Y esto significa que, dado un fragmento de lenguaje natural, somos buenos para entenderlo como Wolfram Language, que luego podemos ir y calcular desde:
Pero, ¿qué pasa con el procesamiento del lenguaje natural (PNL), en el que tomamos pasajes potencialmente largos del lenguaje natural y no intentamos comprenderlos por completo, sino que solo encontramos o procesamos características particulares de ellos? Funciones como
TextSentences ,
TextStructure ,
TextCases y
WordCounts nos han brindado capacidades básicas en esta área por un tiempo. Pero en la Versión 12.0, al hacer uso del último aprendizaje automático, así como nuestras capacidades de base de conocimiento y NLU de larga data, ahora hemos pasado a tener capacidades de PNL muy fuertes.
La pieza central es la versión dramáticamente mejorada de
TextCases . El objetivo básico de
TextCases es encontrar casos de diferentes tipos de contenido en una pieza de texto. Un ejemplo de esto es la clásica tarea de PNL de "reconocimiento de entidades", con
TextCases aquí para encontrar qué nombres de países aparecen en el
artículo de Wikipedia sobre ocelotes :
También podríamos preguntar qué islas se mencionan, pero ahora no pediremos una interpretación de Wolfram Language:
TextCases no es perfecto, pero lo hace bastante bien:
También admite muchos tipos de contenido diferentes:
Puede pedirle que encuentre
pronombres, o cláusulas relativas reducidas , o
cantidades , o
direcciones de correo electrónico , o ocurrencias de cualquiera de los 150 tipos de entidades (como
compañías, plantas o
películas ). También puede pedirle que elija fragmentos de texto que estén en lenguajes
humanos o
informáticos en particular, o que traten
sobre temas particulares (como
viajes o
salud ), o que tengan
un sentimiento positivo o negativo . Y puede usar construcciones como
Contener para pedir combinaciones de estas cosas (como frases nominales que contienen el nombre de un río):
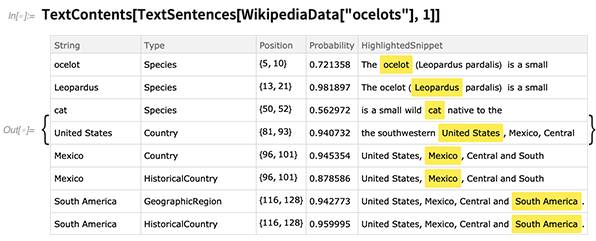
TextContents le permite ver, por ejemplo, detalles de todas las entidades que se detectaron en un texto en particular:
Y sí, en principio se puede usar estas capacidades a través de
FindTextualAnswer para tratar de responder preguntas del texto, pero en un caso como este, los resultados pueden ser bastante extraños:
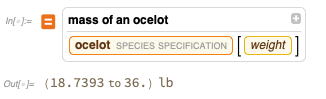
Por supuesto, puede obtener una respuesta real de nuestra base de conocimiento curada incorporada real:
Por cierto, en la Versión 12.0 hemos agregado una variedad de pequeñas "funciones de conveniencia del lenguaje natural", como
Sinónimos y
Antónimos :
Una de las nuevas áreas "sorpresa" en la Versión 12.0 es la química computacional. Hemos tenido datos sobre
productos químicos conocidos explícitos en nuestra base de conocimiento durante mucho tiempo. Pero en la Versión 12.0 podemos calcular con moléculas que se especifican simplemente como objetos simbólicos puros. Así es como podemos especificar lo que resulta ser una molécula de agua:
Y así es como podemos hacer una representación 3D:
Podemos tratar con "productos químicos conocidos":
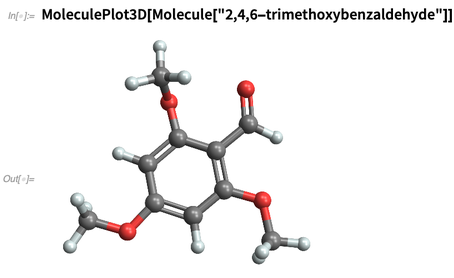
Podemos usar nombres arbitrarios de
IUPAC :
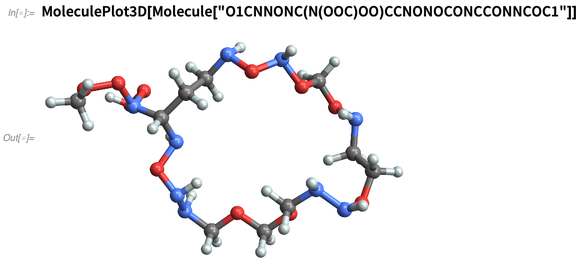
O "inventamos" químicos, por ejemplo, especificándolos por sus cadenas
SMILES :
Pero no solo estamos generando imágenes aquí. También podemos calcular cosas desde la estructura, como las simetrías:
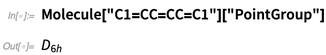
Dada una molécula, podemos hacer cosas como resaltar enlaces carbono-oxígeno:
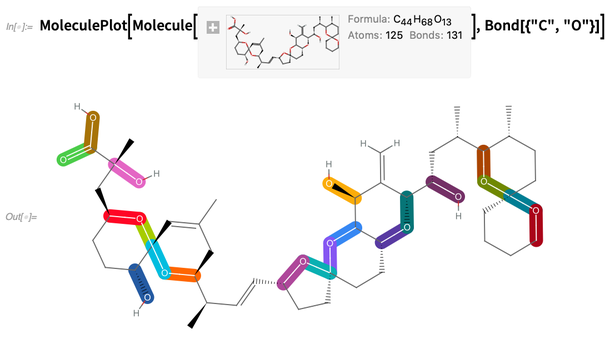
O resalte estructuras, digamos especificadas por cadenas
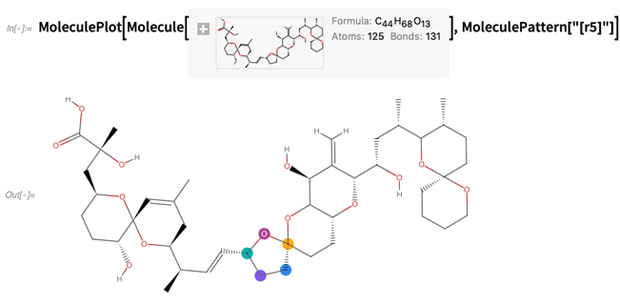
SMARTS (aquí cualquier anillo de 5 miembros):
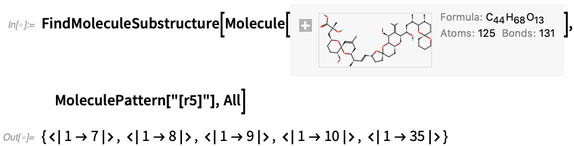
También puede hacer búsquedas de "patrones de moléculas"; los resultados salen en términos de números de átomos:
Las capacidades de química computacional que hemos agregado en la Versión 12.0 son bastante generales y bastante poderosas (con la advertencia de que hasta ahora solo tratan con moléculas orgánicas). En el nivel más bajo, ven las moléculas como gráficos etiquetados con bordes correspondientes a enlaces. Pero también saben de física y explican correctamente las valencias atómicas y las configuraciones de enlaces. No hace falta decir que hay muchos detalles (sobre estereoquímica, simetría, aromaticidad, isótopos, etc.). Pero el resultado final es que la estructura molecular y el cálculo molecular ahora se han agregado con éxito a la lista de áreas que están integradas en Wolfram Language.
Wolfram Language ya tiene fuertes capacidades para la computación geográfica, pero la Versión 12.0 agrega más funciones y mejora algunas de las que ya estaban allí.
Por ejemplo, ahora existe
RandomGeoPosition , que genera una ubicación aleatoria de lat-long. Uno podría pensar que esto sería trivial, pero, por supuesto, uno tiene que preocuparse por las transformaciones de coordenadas, y lo que lo hace mucho más trivial es que uno puede decirle que elija puntos solo dentro de una determinada región, aquí el país de Francia:
Un tema de las nuevas capacidades geográficas en la Versión 12.0 es el manejo no solo de puntos geográficos y regiones, sino también de vectores geográficos. Aquí está el vector de viento actual, por ejemplo, en la posición de la Torre Eiffel, representada como un
GeoVector , con velocidad y dirección (también está
GeoVectorENU , que proporciona componentes este, norte y arriba, así como
GeoGridVector y
GeoVectorXYZ ):
Funciones como
GeoGraphics le permiten visualizar geo vectores discretos.
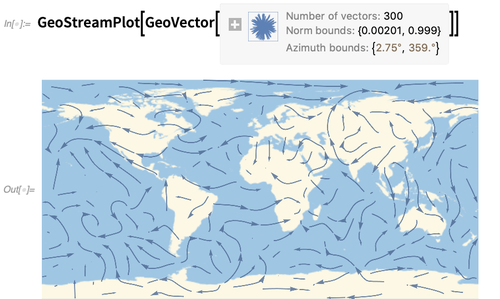
GeoStreamPlot es el análogo geográfico de
StreamPlot (o
ListStreamPlot ), y muestra líneas de
flujo formadas a partir de vectores geográficos (aquí desde
WindDirectionData ):
La geodesia es un área matemáticamente sofisticada, y nos enorgullecemos de hacerlo bien en Wolfram Language. En la versión 12.0, hemos agregado algunas funciones nuevas para completar algunos detalles. Por ejemplo, ahora tenemos funciones como
GeoGridUnitDistance y
GeoGridUnitArea que dan la distorsión (básicamente, valores propios del jacobiano) asociada con diferentes proyecciones geográficas en cada posición en la Tierra (o Luna, Marte, etc.).
Una dirección de visualización que hemos estado desarrollando constantemente es lo que podríamos llamar "meta-gráficos": el etiquetado y la anotación de elementos gráficos. Introdujimos
Callout en la Versión 11.0; en la versión 12.0 se ha extendido a cosas como gráficos 3D:
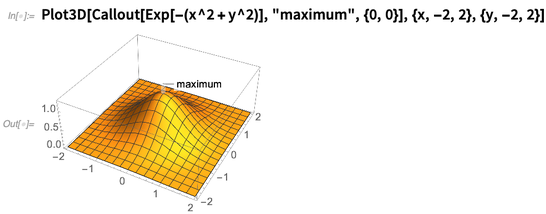
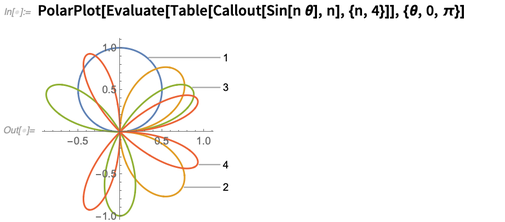
Es bastante bueno para averiguar dónde etiquetar las cosas, incluso cuando se vuelven un poco complejas:
Hay muchos detalles importantes para que los gráficos se vean realmente bien. Algo que se ha mejorado en la Versión 12.0 es garantizar que las columnas de gráficos se alineen en sus marcos, independientemente de la longitud de sus etiquetas de marca. También hemos agregado
LabelVisibility , que le permite especificar las prioridades relativas con las que deben hacerse visibles las diferentes etiquetas.
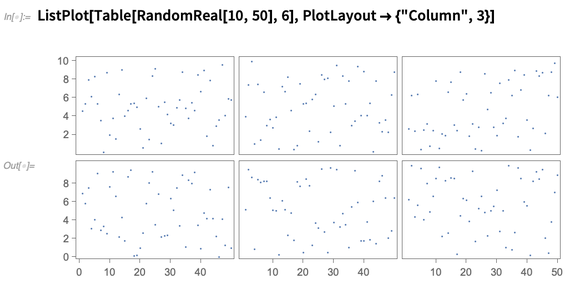
Otra nueva característica de la Versión 12.0 es el diseño de trazado multipanel, donde se muestran diferentes conjuntos de datos en diferentes paneles, pero los paneles comparten ejes siempre que pueden:
Ajuste de la integración de la base de conocimiento
Nuestra base de conocimiento curada, que por ejemplo impulsa a
Wolfram | Alpha, es vasta y está en continuo crecimiento. Y con cada versión de Wolfram Language estamos ajustando progresivamente su integración en el núcleo del lenguaje.
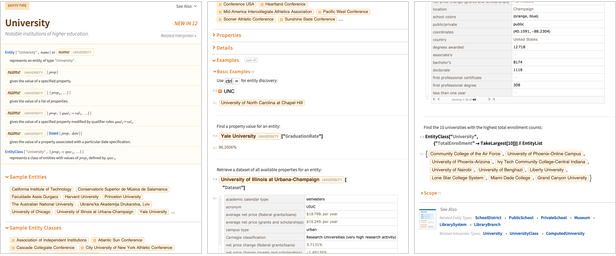
En la Versión 12.0, una cosa que estamos haciendo es exponer cientos de tipos de entidades directamente en el lenguaje:
Antes de la Versión 12.0, las
páginas de ejemplo de Wolfram | Alpha servían como proxy para documentar muchos tipos de entidades. Pero ahora hay documentación de Wolfram Language para todos ellos:
Todavía hay funciones como
SatelliteData ,
WeatherData y
FinancialData que manejan tipos de entidades que rutinariamente necesitan una selección o cálculo complejo. Pero en la Versión 12.0, se puede acceder a cada tipo de entidad de la misma manera, con entrada de
lenguaje natural ("control + =") y entidades y propiedades "en recuadro amarillo":
Por cierto, también se pueden usar entidades implícitamente, como aquí preguntando por los 5 elementos con los puntos de fusión más altos conocidos:
Y uno puede usar
Dated para obtener una serie temporal de valores:
Hemos hecho que sea realmente conveniente trabajar con datos integrados en la base de
conocimiento de Wolfram . Tiene entidades, y es muy fácil preguntar sobre propiedades, etc.
Pero, ¿qué pasa si tienes tus propios datos? ¿Puedes configurarlo para que puedas usarlo tan fácilmente como esto? Una
nueva característica importante de la Versión 11 fue la incorporación de
EntityStore , en el que se pueden
definir los propios tipos de entidad y luego especificar entidades, propiedades y valores.
Wolfram Data Repository contiene un
montón de ejemplos de almacenes de entidades . Aquí hay uno:
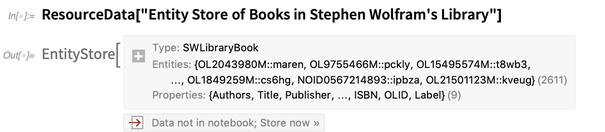
Describe un tipo de entidad única: un
"SWLibraryBook" . Para poder utilizar entidades de este tipo al igual que las entidades integradas, "registramos" el almacén de entidades:
Ahora podemos hacer cosas como pedir 10 entidades aleatorias de tipo
"SWLibraryBook" :
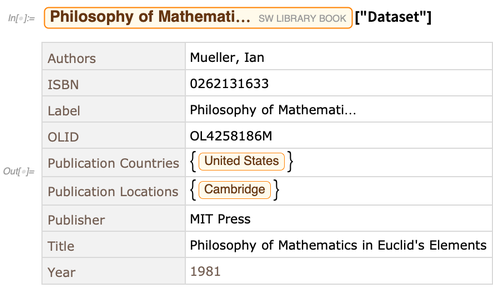
Cada entidad en la tienda de la entidad tiene una variedad de propiedades. Aquí hay un conjunto de datos de los valores de propiedades para una entidad particular:
Bien, pero con esta configuración básicamente estamos leyendo todo el contenido de una entidad almacenada en la memoria. Esto hace que sea muy eficiente hacer cualquier operación de Wolfram Language que uno desee. Pero no es una buena solución escalable para grandes cantidades de datos, por ejemplo, datos que son demasiado grandes para caber en la memoria.
Pero, ¿cuál es una fuente típica de datos grandes? Muy a menudo es una base de datos, y generalmente una relacional a la que se puede acceder usando
SQL . Hemos tenido nuestro
paquete DatabaseLink para acceso de lectura y escritura de bajo nivel a bases de datos SQL durante más de una década. Pero en la Versión 12.0 estamos agregando algunas características incorporadas importantes que permiten manejar bases de datos relacionales externas en Wolfram Language al igual que las tiendas de entidades, o partes integradas de Wolfram Knowledgebase.
Comencemos con un ejemplo de juguete. Aquí hay una representación simbólica de una pequeña base de datos relacional que se almacena en un archivo:
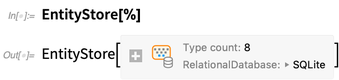
Inmediatamente obtenemos un cuadro que resume lo que hay en la base de datos y nos dice que esta base de datos tiene 8 tablas. Si abrimos la caja, podemos comenzar a inspeccionar la estructura de esas tablas:
Luego podemos configurar esta base de datos relacional como un almacén de entidades en Wolfram Language. Se parece mucho a la tienda de entidades de libros de la biblioteca anterior, pero ahora los datos reales no se guardan en la memoria; en su lugar, todavía está en la base de datos relacional externa, y solo estamos definiendo una asignación ("similar a ORM") a entidades en Wolfram Language:
Ahora podemos registrar esta tienda de entidades, que configura un grupo de tipos de entidades que (al menos de manera predeterminada) llevan el nombre de los nombres de las tablas en la base de datos:
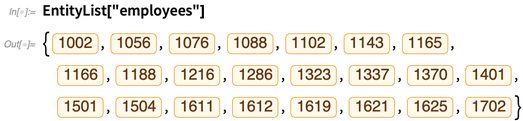
Y ahora podemos hacer "cálculos de entidad" en estos, al igual que lo haríamos en entidades integradas en la base de conocimiento de Wolfram. Cada entidad aquí corresponde a una fila en la tabla "empleados" en la base de datos:
Para un tipo de entidad dado, podemos preguntar qué propiedades tiene. Estas "propiedades" corresponden a columnas en la tabla en la base de datos subyacente:
Ahora podemos preguntar por el valor de una propiedad particular de una entidad particular:
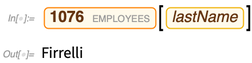
También podemos elegir entidades dando criterios; aquí pedimos entidades de "pagos" con los 4 valores más grandes de la propiedad "cantidad":
Igualmente podemos pedir los valores de estas cantidades mayores:
De acuerdo, pero aquí es donde se vuelve más interesante: hasta ahora hemos estado mirando una pequeña base de datos respaldada por archivos. Pero podemos hacer exactamente lo mismo con una base de datos gigante alojada en un servidor externo.
Como ejemplo, conectemos a la
base de datos OpenStreetMap PostgreSQL del tamaño de un terabyte que contiene lo que es básicamente el mapa de calles del mundo:
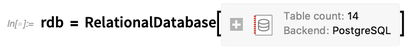
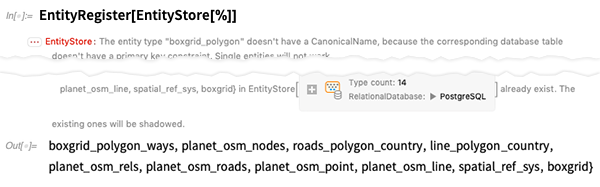
Como antes, registremos las tablas en esta base de datos como tipos de entidad. Como la mayoría de las bases de datos en la naturaleza, hay pequeños problemas técnicos en la estructura, que se solucionan, pero generan advertencias:
Pero ahora podemos hacer preguntas sobre la base de datos, como cuántos puntos geográficos o "nodos" hay en todas las calles del mundo (y, sí, es un gran número, por eso la base de datos es grande):
Aquí pedimos los nombres de los objetos con las 10 áreas más grandes (proyectadas) en la tabla planet_osm_polygon (101 GB) (y, sí, toma menos de un segundo):
Entonces, ¿cómo funciona todo esto? Básicamente, lo que sucede es que nuestra representación de Wolfram Language se está compilando en consultas SQL de bajo nivel que luego se envían para ejecutarse directamente en el servidor de la base de datos.
A veces, solicitará resultados que sean solo valores finales (como, por ejemplo, las "cantidades" anteriores). Pero en otros casos querrás algo intermedio, como una colección de entidades que han sido seleccionadas de una manera particular. Y, por supuesto, esta colección podría tener mil millones de entradas. Entonces, una característica muy importante de lo que estamos presentando en la Versión 12.0 es que podemos representar y manipular tales cosas de manera puramente simbólica, resolviéndolas a algo específico solo al final.
Volviendo a nuestra base de datos de juguetes, aquí hay un ejemplo de cómo especificaríamos una clase de entidades obtenidas agregando el
límite de
crédito total para todos los
clientes con un valor de
país dado:
Al principio, esto es solo algo simbólico. Pero si solicitamos valores específicos, se realizan consultas de bases de datos reales y obtenemos resultados específicos:
Hay una familia de nuevas funciones para configurar diferentes tipos de consultas. Y las funciones en realidad funcionan no solo para bases de datos relacionales, sino también para almacenes de entidades y para la base de conocimiento Wolfram incorporada. Entonces, por ejemplo, podemos pedir la masa atómica promedio para un período dado en la
tabla periódica de elementos :
Una nueva construcción importante es
EntityFunction .
EntityFunction es como
Function , excepto que sus variables representan entidades (o clases de entidades) y describe operaciones que pueden realizarse directamente en bases de datos externas. Aquí hay un ejemplo con datos integrados, en el que estamos definiendo una clase de entidad "filtrada" en la que el criterio de filtrado es una función que prueba los valores de la población.
FilteredEntityClass en sí solo se representa simbólicamente, pero
EntityList realmente realiza la consulta y resuelve una lista explícita de entidades (aquí, sin clasificar):
Además de
EntityFunction ,
AggregatedEntityClass y
SortedEntityClass , la versión 12.0 incluye
SampledEntityClass (para obtener algunas entidades de una clase),
ExtendedEntityClass (para agregar propiedades calculadas) y
CombinedEntityClass (para combinar propiedades de diferentes clases). Con estas primitivas, uno puede construir todas las operaciones estándar de "
álgebra relacional ".
En la programación estándar de bases de datos, uno generalmente termina con toda una jungla de "combinaciones" y "claves foráneas", etc. Nuestra representación de Wolfram Language le permite operar a un nivel superior, donde básicamente las uniones se convierten en composición de funciones y las claves externas son solo diferentes tipos de entidades. (Sin embargo, si desea hacer uniones explícitas, puede hacerlo, por ejemplo, usando
CombinedEntityClass ).
Lo que sucede debajo del capó es que todas esas construcciones de Wolfram Language se están compilando en SQL o, más exactamente, el dialecto específico de
SQL que es adecuado para la base de datos particular que está utilizando (actualmente
admitimos SQLite ,
MySQL ,
PostgreSQL y
MS -SQL , con soporte para
OracleSQL próximamente). Cuando hacemos la compilación, verificamos automáticamente los tipos, para asegurarnos de que obtenga una consulta significativa. Incluso las especificaciones bastante simples de Wolfram Language pueden terminar convirtiéndose en muchas líneas de SQL. Por ejemplo,
produciría el siguiente SQL intermedio (aquí para consultar la base de datos SQLite):
El sistema de integración de bases de datos que tenemos en la Versión 12.0 es bastante sofisticado, y hemos estado trabajando en ello durante bastantes años. Es un importante paso adelante al permitir que Wolfram Language maneje directamente un nuevo nivel de "grandeza" en big data, y permitir que Wolfram Language haga ciencia de datos directamente en conjuntos de datos del tamaño de terabytes y más. Como encontrar qué entidades callejeras en el mundo tienen "Wolfram" en su nombre:
¿Cuál es la mejor manera de representar el conocimiento sobre el mundo? Es un tema que ha sido debatido por filósofos (y otros) desde la antigüedad. A veces la gente decía que la lógica era la clave. A veces las matemáticas. A veces bases de datos relacionales. Pero ahora al menos conocemos una base sólida (o al menos, estoy bastante seguro de que lo sabemos): todo se puede representar mediante el cálculo. Esta es una idea poderosa, y en cierto sentido eso es lo que hace posible todo lo que hacemos con Wolfram Language.
Pero, ¿existen subconjuntos de cómputo general que sean útiles para representar al menos ciertos tipos de conocimiento? Uno que utilizamos ampliamente en la base de
conocimiento de Wolfram es la noción de entidades ("Ciudad de Nueva York"), propiedades ("población") y sus valores ("8.6 millones de personas"). Por supuesto, tales triples no representan todo el conocimiento del mundo ("¿cuál será la posición de Marte mañana?"). Pero son un comienzo decente cuando se trata de ciertos tipos de conocimiento "estático" sobre cosas distintas.
Entonces, ¿cómo se puede formalizar este tipo de representación del conocimiento? Una respuesta es a través de bases de datos de gráficos. Y en la Versión 12.0, en alineación con muchos proyectos de
"web semántica" ,
admitimos bases de datos de gráficos usando
RDF y consultas en contra de ellos usando
SPARQL . En RDF, el objeto central es un
IRI ("Identificador de recursos internacionalizados"), que puede representar una entidad o una propiedad. Un "
triplestore " consiste entonces en una colección de triples ("sujeto", "predicado", "objeto"), con cada elemento en cada triple siendo un IRI (o un literal, como un número). Todo el objeto se puede considerar como una base de datos de gráficos o un almacén de gráficos, o, matemáticamente, una hipergrafía. (Es una
hipergrafía porque el predicado "bordes" también puede ser vértices en otros lugares).
Puede crear su propio
RDFStore de la misma manera que crea un
EntityStore, y de hecho puede consultar cualquier Wolfram Language
EntityStore usando SPARQL al igual que consulta un
RDFStore . Y dado que la parte de propiedad de entidad de Wolfram Knowledgebase puede tratarse como un almacén de entidades, también puede consultar esto. Entonces, aquí, finalmente, es un ejemplo. La lista de país-ciudad
Entidad ["
País "],
Entidad ["
Ciudad "]} en efecto representa una tienda RDF. Entonces
SPARQLSelect es un operador que actúa en esta tienda. Lo que hace es intentar encontrar un triple que coincida con lo que está pidiendo, con un valor particular para la "variable SPARQL" x:
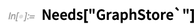
Por supuesto, también hay una manera mucho más simple de hacer esto en Wolfram Language:
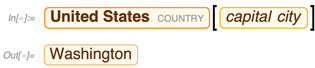
Pero con SPARQL puede hacer cosas mucho más exóticas, como preguntar qué propiedades relacionan los Estados Unidos con México:
O si hay un camino basado en la relación entre países limítrofes desde Portugal a Alemania:
En principio, puede escribir una consulta SPARQL como una cadena (un poco como si pudiera escribir una cadena SQL). Pero lo que hemos hecho en la Versión 12.0 es introducir una representación simbólica de SPARQL que permite el cálculo de la representación en sí misma, lo que facilita, por ejemplo, generar automáticamente consultas SPARQL complejas. (Y es particularmente importante hacer esto porque, por sí mismas, las consultas SPARQL prácticas tienen la costumbre de ser extremadamente largas y pesadas).
Bien, pero ¿hay tiendas RDF en la naturaleza? Ha sido una esperanza a largo plazo que una gran parte de la web de alguna manera se etiquete lo suficiente como para "volverse semántica" y, de hecho, sea una tienda RDF gigante. Sería genial si esto sucediera, pero hasta ahora definitivamente no ha sucedido. Aún así, hay algunas tiendas RDF públicas por ahí, y también algunas tiendas RDF dentro de las organizaciones, y con nuestras nuevas capacidades en la Versión 12.0, estamos en una posición única para hacer cosas interesantes con ellas.
Una forma increíblemente común de problema en las aplicaciones industriales de las matemáticas es: "¿Qué configuración minimiza el costo (o maximiza la recompensa) si se deben cumplir ciertas restricciones?" Hace más de medio siglo, el llamado
algoritmo simplex se inventó para resolver versiones lineales de este tipo de problema, en el que tanto la función objetivo (costo, beneficio) como las restricciones son funciones lineales de las variables en el problema. En la década de 1980 se habían inventado métodos mucho más eficientes ("punto interior"), y los hemos tenido para hacer "
programación lineal " en Wolfram Language durante mucho tiempo.
¿Pero qué pasa con los problemas no lineales? Bueno, en el caso general, uno puede usar funciones como NMinimize. Y hacen un trabajo de vanguardia. Pero es un problema difícil. Sin embargo, hace algunos años, se hizo evidente que, incluso entre los problemas de optimización no lineal, existe una clase de los llamados problemas de optimización convexa que en realidad pueden resolverse casi tan eficientemente como los lineales. ("Convexo" significa que tanto el objetivo como las restricciones involucran solo funciones convexas, de modo que nada puede "moverse" cuando uno se acerca a un extremo, y no puede haber ningún mínimo local que no sea mínimo global).
En la versión 12.0, ahora tenemos implementaciones sólidas para todas las diversas clases estándar de optimización convexa. Aquí hay un caso simple, que implica minimizar una forma cuadrática con un par de restricciones lineales:
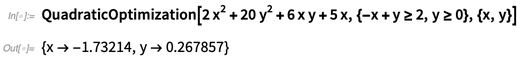NMinimize ya podría
resolver este problema en particular en la Versión 11.3:
Pero si uno tuviera más variables, el antiguo
NMinimize se empantanaría rápidamente. Sin embargo, en la versión 12.0, la
optimización cuadrática continuará funcionando bien, hasta más de 100,000 variables con más de 100,000 restricciones (siempre que sean bastante escasas).
En la Versión 12.0 tenemos funciones de "optimización convexa en bruto" como
SemidefiniteOptimization (que maneja desigualdades de matriz lineal) y
ConicOptimization (que maneja desigualdades de vector lineal). Pero funciones como
NMinimize y
FindMinimum también reconocerán automáticamente cuándo un problema puede resolverse de manera eficiente al transformarse en un formulario de optimización convexo.
¿Cómo se configuran los problemas de optimización convexa? Los más grandes implican restricciones en vectores enteros o matrices de variables. Y en la Versión 12.0 ahora tenemos funciones como
VectorGreaterEqual (entrada como ≥) que pueden representarlas inmediatamente.
Las ecuaciones diferenciales parciales son difíciles, y hemos estado trabajando en formas cada vez más sofisticadas y generales para manejarlas durante 30 años. Primero presentamos
NDSolve (para ODE) en la
Versión 2, en 1991 . Tuvimos nuestras primeras PDE numéricas (1 + 1-dimensionales) a mediados de la década de 1990. En 2003 presentamos nuestro potente marco modular para manejar ecuaciones diferenciales numéricas. Pero en términos de PDE, básicamente solo estábamos tratando con regiones simples y rectangulares. Ir más allá de eso requería construir todo nuestro
sistema de geometría computacional , que presentamos en la Versión 10. Y con esto, lanzamos
nuestros primeros solucionadores PDE de elementos finitos . En la Versión 11, generalizamos a
problemas propios .
Ahora, en la Versión 12, presentamos otra generalización importante: el análisis de elementos finitos no lineales. El análisis de elementos finitos implica descomponer regiones en pequeños triángulos discretos, tetraedros, etc., en los cuales el PDE original puede aproximarse mediante un gran número de ecuaciones acopladas. Cuando el PDE original es lineal, estas ecuaciones también serán lineales, y ese es el caso típico que las personas consideran cuando hablan de "análisis de elementos finitos".
Pero hay muchas PDE de importancia práctica que no son lineales, y para abordarlas se necesita un análisis de elementos finitos no lineales, que es lo que tenemos ahora en la Versión 12.0.
Como ejemplo, esto es lo que se necesita para resolver el PDE desagradablemente no lineal que describe la altura de una superficie mínima 2D (por ejemplo, una película de jabón idealizada), aquí sobre un anillo, con condiciones de contorno (Dirichlet) que hacen que se mueva sinusoidalmente en el bordes (como si la película de jabón estuviera suspendida de cables):
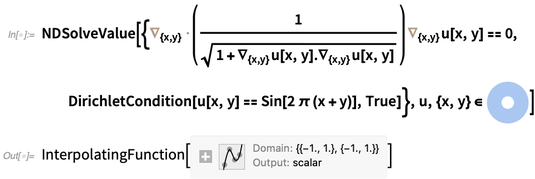
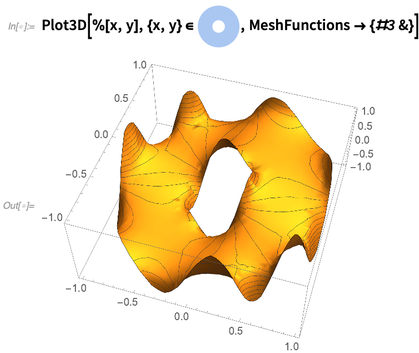
En mi computadora, toma solo un cuarto de segundo resolver esta ecuación y obtener una función de interpolación. Aquí hay una gráfica de la función de interpolación que representa la solución:
Hemos dedicado mucha ingeniería a optimizar la ejecución de los programas de Wolfram Language a lo largo de los años. Ya en 1989 comenzamos a compilar automáticamente cálculos numéricos simples de precisión de máquina con instrucciones para una máquina virtual eficiente (y, de hecho, escribí el código original para esto). Con los años, hemos ampliado las capacidades de este compilador, pero siempre se ha limitado a programas bastante simples.
En la versión 12.0 estamos dando un gran paso adelante y lanzamos la primera versión de un compilador nuevo y mucho más potente en el que hemos estado trabajando durante varios años. Este compilador es capaz de manejar una gama mucho más amplia de programas (incluyendo construcciones funcionales complejas y flujos de control elaborados), y también está compilando no a una máquina virtual sino directamente a un código de máquina nativo optimizado.
En la versión 12.0 todavía consideramos el nuevo compilador experimental. Pero avanza rápidamente, y tendrá un efecto dramático en la eficiencia de muchas cosas en Wolfram Language. En la Versión 12.0, solo estamos exponiendo una "forma de kit" del nuevo compilador, con funciones de compilación específicas. Pero progresivamente haremos que el compilador funcione cada vez más automáticamente, descubriendo con el aprendizaje automático y otros métodos cuando valga la pena tomarse el tiempo para hacer qué nivel de compilación.
A nivel técnico, el nuevo compilador de la Versión 12.0 se basa en LLVM y funciona generando código LLVM, enlazando en la misma biblioteca de tiempo de ejecución de bajo nivel que usa el núcleo Wolfram Language, y llamando al núcleo completo de Wolfram Language para la funcionalidad eso no está en la biblioteca de tiempo de ejecución.
Aquí está la forma básica en que uno compila una función pura en la versión actual del nuevo compilador:
La función de código compilado resultante funciona igual que la función original, aunque más rápido:
Una gran parte de lo que permite a
FunctionCompile producir una función más rápida es que le está diciendo que haga suposiciones sobre el tipo de argumento que obtendrá.
Admitimos muchos tipos básicos (como "
Integer32 " y "
Real64 "). Pero cuando usa
FunctionCompile , se compromete con tipos de argumentos particulares, por lo que se puede generar un código mucho más racionalizado.
Gran parte de la sofisticación del nuevo compilador está asociada a inferir qué tipos de datos se generarán en la ejecución de un programa. (Hay muchos algoritmos teóricos de gráficos y otros involucrados, y no hace falta decir que toda la metaprogramación para el compilador se realiza con Wolfram Language).
Aquí hay un ejemplo que implica un poco de inferencia de tipos (el tipo de
fib se deduce como
"Integer64" -> "Integer64" : una función entera que devuelve un número entero):
En mi computadora,
cf [25] se ejecuta unas 300 veces más rápido que la función sin compilar. (Por supuesto, la versión compilada falla cuando su salida ya no es del tipo "
Integer64 ", pero la versión estándar de Wolfram Language continúa funcionando bien).
El compilador ya puede manejar cientos de primitivas de programación de Wolfram Language, rastreando adecuadamente qué tipos se producen y genera código que implementa directamente estas primitivas. A veces, sin embargo, uno querrá usar funciones sofisticadas en Wolfram Language para las cuales no tiene sentido generar el código compilado propio, y donde lo que realmente quiere hacer es llamar al núcleo de Wolfram Language para estas funciones . En la versión 12.0,
KernelFunction permite hacer esto:
OK, pero digamos que uno tiene una función de código compilado. ¿Qué se puede hacer con eso? Bueno, antes que nada uno puede ejecutarlo dentro del Wolfram Language. Uno también puede almacenarlo y ejecutarlo más tarde. Cualquier compilación particular se realiza para una arquitectura de procesador específica (por ejemplo, x86 de 64 bits). Pero
CompiledCodeFunction mantiene automáticamente suficiente información para realizar compilaciones adicionales para una arquitectura diferente si es necesario.
Pero dada una función
CompiledCode , una de las nuevas posibilidades interesantes es que se puede generar directamente un código que se puede ejecutar incluso fuera del entorno Wolfram Language. (Nuestro antiguo compilador tenía el paquete
CCodeGenerate que proporcionaba capacidades ligeramente similares en casos simples, aunque incluso entonces se basa en una compleja cadena de herramientas de compiladores C, etc.)
Así es como se puede exportar código LLVM sin formato (observe que cosas como la optimización de recursión de cola se realizan automáticamente, y observe también la función simbólica y las opciones del compilador al final):
Si se utiliza
FunctionCompileExportLibrary , se obtiene un archivo de biblioteca: .dylib en Mac, .dll en Windows y .so en Linux. Uno puede usar esto en Wolfram Language haciendo
LibraryFunctionLoad . Pero también se puede usar en un programa externo.
Una de las cosas principales que determina la generalidad del nuevo compilador es la riqueza de su sistema de tipos. En este momento, el compilador admite
14 tipos atómicos (como "
Boolean ", "
Integer8 ", "
Complex64 ", etc.). También admite constructores de tipos como "
PackedArray ", de modo que, por ejemplo,
TypeSpecifier ["
PackedArray "] [
"Real64", 2 ] corresponde a una matriz empaquetada de rango real de 64 bits.
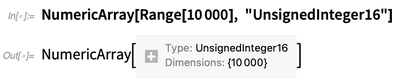
En la implementación interna del Wolfram Language (que, por cierto, está principalmente en Wolfram Language) hemos tenido una forma optimizada de almacenar matrices durante mucho tiempo. En la Versión 12.0 lo estamos exponiendo como
NumericArray . A diferencia de las construcciones ordinarias de Wolfram Language, debe decirle a
NumericArray en detalle cómo debe almacenar los datos. Pero luego funciona de una manera agradable y optimizada:
En la Versión 11.2 presentamos
ExternalEvaluate , que le permite hacer cálculos en lenguajes como
Python y
JavaScript desde Wolfram Language (en
Python , "^" significa
BitXor ):
En la Versión 11.3, introdujimos celdas de lenguaje externo, para facilitar el ingreso de programas de lenguaje externo u otra entrada directamente en un cuaderno:
En la versión 12.0, estamos ajustando la integración. Por ejemplo, dentro de una cadena de idioma externa, puede usar <* ... *> para proporcionar el código de Wolfram Language para evaluar:
Esto también funciona en celdas de lenguaje externo:
Por supuesto, Python no es Wolfram Language, por lo que muchas cosas no funcionan:
Pero
ExternalEvaluate puede al menos devolver muchos tipos de datos de Python, incluidas listas (como
Lista ), diccionarios (como
Asociación ), imágenes (como
Imagen ), fechas (como
DateObject ),
matrices NumPy (como
NumericArray ) y
conjuntos de datos de pandas (como
TimeSeries ,
DataSet , etc.). (
ExternalEvaluate también puede devolver
ExternalObject que es básicamente un identificador de un objeto que puede enviar de vuelta a Python).
También puede usar directamente funciones externas (el ord ligeramente llamado es básicamente el análogo de Python de
ToCharacterCode ):
Y aquí hay una función pura de Python, representada simbólicamente en Wolfram Language:
Llamar al lenguaje Wolfram desde Python y otros lugares
¿Cómo se debe acceder al Wolfram Language? Hay muchas formas Se puede usar directamente en un cuaderno. Uno puede
llamar a las API que lo ejecutan en la nube. O uno puede usar
WolframScript en un
shell de línea de comandos . WolframScript puede ejecutarse en un
Wolfram Engine local o en un
Wolfram Engine en la nube . Te permite dar directamente el código para ejecutar:
Y le permite hacer cosas como definir funciones, por ejemplo, con código en un archivo:
Junto con el lanzamiento de la Versión 12.0, también estamos lanzando nuestra primera nueva
Biblioteca de cliente Wolfram Language, para Python. La idea básica de esta biblioteca es facilitar que los programas de Python llamen Wolfram Language. (Vale la pena señalar que efectivamente hemos tenido una Biblioteca de cliente de lenguaje C durante no menos de 30 años, a través de lo que ahora se llama
WSTP ).
La forma en que funciona una Biblioteca de Client Language es diferente para diferentes idiomas. For Python—as an interpreted language (that was actually historically informed by early Wolfram Language)—it's particularly simple. After you
set up the library , and start a session (locally or in the cloud), you can then just evaluate Wolfram Language code and get the results back in Python:
You can also directly access Wolfram Language functions (as a kind of inverse of
ExternalFunction ):
And you can directly interact with things like pandas structures, NumPy arrays, etc. In fact, you can in effect just treat the whole of the Wolfram Language like a giant library that can be accessed from Python. Or, of course, you can just use the nice, integrated Wolfram Language directly, perhaps creating external APIs if you need them.
More for the Wolfram “Super Shell”
One feature of using the Wolfram Language is that it lets you get away from having to think about the details of your computer system, and about things like files and processes. But sometimes one wants to work at a systems level. And for fairly simple operations, one can just use an operating system GUI. But what about for more complicated things? In the past I usually found myself using the
Unix shell . But for a long time now, I've instead used Wolfram Language.
It's certainly very convenient to have everything in a notebook, and it's been great to be able to programmatically use functions like
FileNames (ls),
FindList (grep),
SystemProcessData (ps),
RemoteRunProcess (ssh) and
FileSystemScan . But in Version 12.0 we're adding a bunch of additional functions to support using the Wolfram Language as a “super shell”.
There's
RemoteFile for symbolically representing a remote file (with authentication if needed)— that you can immediately use in functions like
CopyFile . There's
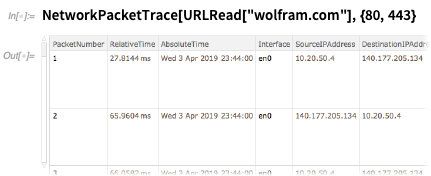
FileConvert for directly converting files between different formats.
And if you really want to dive deep, here's how you'd trace all the packets on ports 80 and 443 used in reading from
wolfram.com :
Puppeting a Web Browser
Within the Wolfram Language, it's been easy for a long time to interact with web servers, using functions like
URLExecute and
HTTPRequest , as well as $
Cookies , etc. But in Version 12.0 we're adding something new: the ability of the Wolfram Language to
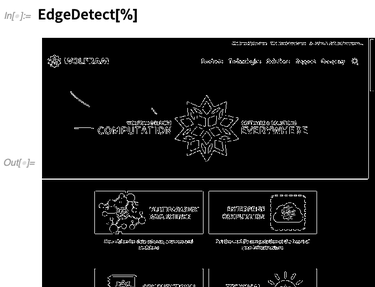
control a web browser , and programmatically make it do what we want. The most immediate thing we can do is just to get an image of what a website looks like to a web browser:
The result is an image that we can compute with:
To do something more detailed, we have to start a browser session (we currently support Firefox and Chrome):
Immediately a blank browser window appears on our screen. Now we can use WebExecute to open a webpage:
Now that we've opened the page, there are lots of commands we can run. This clicks the first hyperlink containing the text “Programming Lab”:
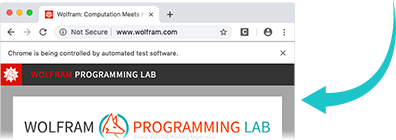
This returns the title of the page we've reached:
You can type into fields, run JavaScript, and basically do programmatically anything you could do by hand with a web browser. Needless to say, we've been using a version of this technology for years inside our company to test all our various websites and web services. But now, in Version 12.0, we're making a streamlined version generally available.
For every general-purpose computer in the world today, there are probably 10 times as many
microcontrollers —running specific computations without any general operating system. A microcontroller might cost a few cents to a few dollars, and in something like a mid-range car, there might be 30 of them.
In Version 12.0 we're introducing a
Microcontroller Kit for the Wolfram Language, that lets you give symbolic specifications from which it automatically generates and deploys code to run autonomously in microcontrollers. In the typical setup, a microcontroller is continuously doing computations on data coming in from sensors, and in real time putting out signals to actuators. The most common types of computations are effectively ones in control theory and signal processing.
We've had extensive support for doing
control theory and
signal processing directly in the Wolfram Language for a long time. But now what's possible with the Microcontroller Kit is to take what's specified in the language and download it as embedded code in a standalone microcontroller that can be
deployed anywhere (in devices, IoT, appliances, etc.).
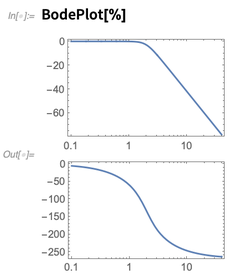
As an example, here's how one can generate a symbolic representation of an analog signal-processing filter:
We can use this filter directly in the Wolfram Language—say using
RecurrenceFilter to apply it to an audio signal. We can also do things like plot its frequency response:
To deploy the filter in a microcontroller, we first have to derive from this continuous-time representation a discrete-time approximation that can be run in a tight loop (here, every 0.1 seconds) in the microcontroller:
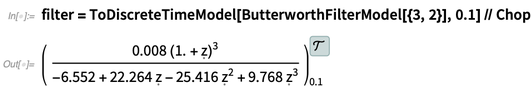
Now we're ready to use the Microcontroller Kit to actually deploy this to a microcontroller. The kit supports more than a hundred different types of microcontrollers. Here's how we could deploy the filter to an
Arduino Uno that we have connected to a serial port on our computer:
MicrocontrollerEmbedCode works by generating appropriate C-like source code, compiling it for the microcontroller architecture you want, then actually deploying it to the microcontroller through its so-called programmer. Here's the actual source code that was generated in this particular case:
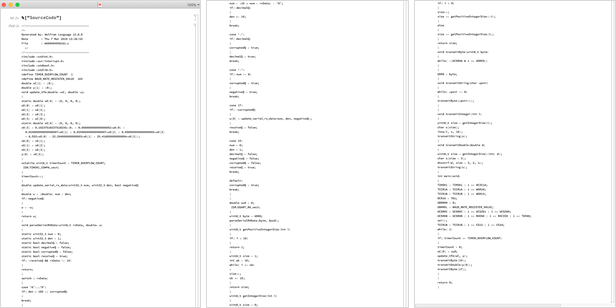
So now we have a thing like this that runs our
Butterworth filter , that we can use anywhere:
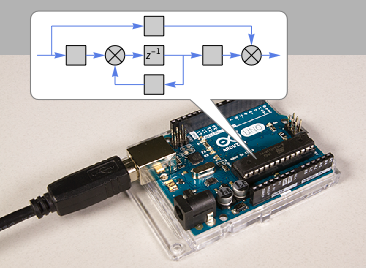
If we want to check what it's doing, we can always connect it back into the Wolfram Language using
DeviceOpen to open its
serial port , and read and write from it.
What's the relation between the Wolfram Language and video games? Over the years, the Wolfram Language has been used behind the scenes in
many aspects of game development (simulating strategies, creating geometries, analyzing outcomes, etc.). But for some time now we've been working on a closer link between Wolfram Language and the
Unity game environment , and in Version 12.0 we're releasing a first version of this link.
The basic scheme is to have Unity running alongside the Wolfram Language, then to set up two-way communication, allowing both objects and commands to be exchanged. The under-the-hood plumbing is quite complex, but the result is a nice merger of the strengths of Wolfram Language and Unity.
This sets up the link, then starts a new project in Unity:
Now create some complex shape:
Then it takes just one command to put this into the Unity game as an object called "
thingoid ":
Within the Wolfram Language there's a symbolic representation of the object, and UnityLink now provides hundreds of functions for manipulating such objects, always maintaining versions both in Unity and in the Wolfram Language.
It's very powerful that one can take things from the Wolfram Language and immediately put them into Unity—whether they're
geometry ,
images ,
audio ,
geo terrain ,
molecular structures ,
3D anatomy , or whatever. It's also very powerful that such things can then be manipulated within the Unity game, either through things like game physics, or by user action. (Eventually, one can expect to have
Manipulate -like functionality, in which the controls aren't just sliders and things, but complex pieces of gameplay.)
We've done experiments with putting Wolfram Language–generated content into virtual reality since the early 1990s. But in modern times Unity has become something of a de facto standard for setting up VR/AR environments—and with UnityLink it's now straightforward to routinely put things from Wolfram Language into any modern XR environment.
One can use the Wolfram Language to prepare material for Unity games, but within a Unity game UnityLink also basically lets one just insert Wolfram Language code that can be executed during a game either on a local machine or through an API in the
Wolfram Cloud . And, among other things, this makes it straightforward to put hooks into a game so the game can send “telemetry” (say to the
Wolfram Data Drop ) for analysis in the Wolfram Language. (It's also possible to script the playing of the game—which is, for example, very useful for game testing.)
Writing games is a complex matter. But UnityLink provides an interesting new approach that should make it easier to prototype all sorts of games, and to learn the ideas of game development. One reason for this is that it effectively lets one script a game at a higher level by using symbolic constructs in the Wolfram Language. But another reason is that it lets the development process be done incrementally in a notebook, and explained and documented every step of the way. For example, here's what amounts to a
computational essay describing the development of a “
piano game ”:
UnityLink isn't a simple thing: it contains more than 600 functions. But with those functions it's possible to access pretty much all the capabilities of Unity, and to set up pretty much any imaginable game.
For something like reinforcement learning it's essential to have a manipulable external environment in the loop when one's doing machine learning. Well,
ServiceExecute lets you call APIs (what's the effect of posting that tweet, or making that trade?), and
DeviceExecute lets you actuate actual devices (turn the robot left) and get data from sensors (did the robot fall over?).
But for many purposes what one instead wants is to have a simulated external environment. And in a way, just the pure Wolfram Language already to some extent does that, for example providing access to a rich “computational universe” full of modifiable programs and equations (
cellular automata ,
differential equations , …). And, yes, the things in that computational universe can be informed by the real world—say with the realistic properties of
oceans , or
chemicals or
mountains .
But what about environments that are more like the ones we modern humans typically learn in—full of built engineering structures and so on? Conveniently enough,
SystemModel gives access to lots of realistic engineering systems. And through UnityLink we can expect to have access to rich game-based simulations of the world.
But as a first step, in Version 12.0 we're setting up connections to some simple games—in particular from the
OpenAI “gym” . The interface is much as it would be for interacting with the real world, with the game accessed like a “device” (after appropriate sometimes-“open-source-painful” installation):
We can read the state of the game:
And we can show it as an image:
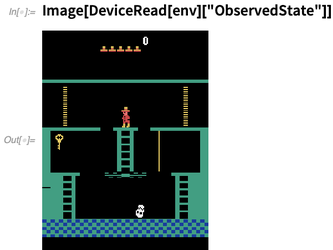
With a bit more effort, we can take 100 random actions in the game (always checking that we didn't “die”), then show a feature space plot of the observed states of the game:
In Version 11.3 we began
our first connection to the blockchain . Version 12.0 adds a lot of new features and capabilities, perhaps most notably the ability to write to public blockchains, as well as read from them. (We also have our own
Wolfram Blockchain for Wolfram Cloud users.) We're currently supporting
Bitcoin ,
Ethereum and
ARK blockchains, both their mainnets and testnets (and, yes, we have our own nodes connecting directly to these blockchains).
In Version 11.3 we allowed
raw reading of transactions from blockchains. In Version 12.0 we've added a layer of analysis, so that, for example, you can ask for a summary of “CK” tokens (AKA
CryptoKitties ) on the
Ethereum blockchain:
It's quick to look at all token transactions in history, and make a word cloud of how active different tokens have been:
But what about doing our own transaction? Let's say we want to use a
Bitcoin ATM (like the one that, bizarrely,
exists at a bagel store near me ) to transfer cash to a Bitcoin address. Well, first we create our crypto keys (and we need to make sure we remember our private key!):
Next, we have to take our public key and generate a Bitcoin address from it:
Make a QR code from that and you're ready to go to the ATM:
But what if we want to write to the blockchain ourselves? Here we'll use the Bitcoin testnet (so we're not spending real money). This shows an output from a transaction we did before—that includes 0.0002 bitcoin (ie 20,000 satoshi):
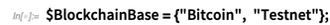
Now we can set up a transaction which takes this output, and, for example, sends 8000 satoshi to each of two addresses (that we defined just like for the ATM transaction):
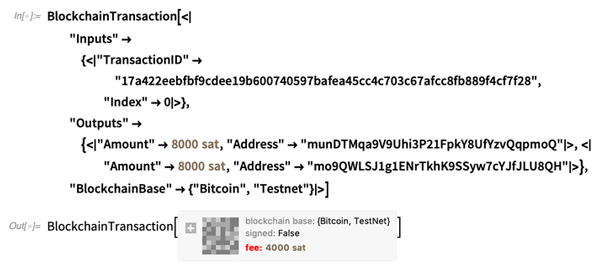
OK, so now we've got a blockchain transaction object—that would offer a fee (shown in red because it's “actual money” you'll spend) of all the leftover cryptocurrency (here 4000 satoshi) to a miner willing to put the transaction in the blockchain. But before we can submit this transaction (and “spend the money”) we have to sign it with our private key:
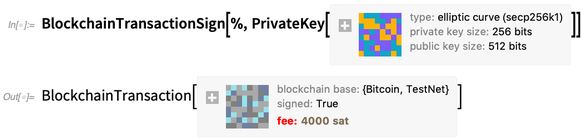
Finally, we just apply
BlockchainTransactionSubmit and we've submitted our transaction to be put on the blockchain:
Here's its transaction ID:
If we immediately ask about this transaction, we'll get a message saying it isn't in the blockchain:
But after we wait a few minutes, there it is—and it'll soon spread to every copy of the Bitcoin testnet blockchain:
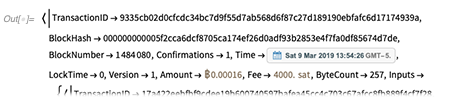
If you're prepared to spend real money, you can use exactly the same functions to do a transaction on a main net. You can also do things like buy CryptoKitties. Functions like
BlockchainContractValue can be used for any (for now, only Ethereum) smart contract, and are set up to immediately understand things like
ERC-20 and
ERC-721 tokens.
Dealing with blockchains involves lots of cryptography, some of which is new in Version 12.0 (notably, handling elliptic curves). But in Version 12.0 we're also extending our non-blockchain cryptographic functions. For example, we've now got functions for directly dealing with
digital signatures . This creates a digital signature using the private key from above:
Now anyone can verify the message using the corresponding public key:
In Version 12.0, we added several new types of hashes for the
Hash function, particularly to support various cryptocurrencies. We also added ways to generate and verify
derived keys . Start from any password, and
GenerateDerivedKey will “puff it out” to something longer (to be more secure you should add “
salt ”):
Here's a version of the derived key, suitable for use in various authentication schemes:
Connecting to Financial Data Feeds
The
Wolfram Knowledgebase contains all sorts of
financial data . Typically there's a
financial entity (like a stock), then there's a property (like price). Here's the complete daily history of Apple's stock price (it's very impressive that it looks best on a log scale):
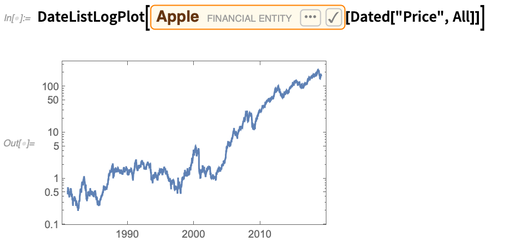
But while the financial data in the Wolfram Knowledgebase, and standardly available in the Wolfram Language, is continuously updated, it's not real time (mostly it's 15-minute delayed), and it doesn't have all the detail that many financial traders use. For serious finance use, however, we've developed
Wolfram Finance Platform . And now, in Version 12.0, it's got direct access to Bloomberg and Reuters financial data feeds.
The way we architect the Wolfram Language, the framework for the connections to Bloomberg and Reuters is always available in the language—but it's only activated if you have Wolfram Finance Platform, as well as the appropriate Bloomberg or Reuters subscriptions. But assuming you have these, here's what it looks like to connect to the
Bloomberg Terminal service:
All the financial instruments handled by the Bloomberg Terminal now become available as entities in the Wolfram Language:
Now we can ask for properties of this entity:
Altogether there are more than 60,000 properties accessible from the Bloomberg Terminal:
Here are 5 random examples (yes, they're pretty detailed; those are Bloomberg names, not ours):
We support the Bloomberg Terminal service, the
Bloomberg Data License service, and the
Reuters Elektron service. One sophisticated thing one can now do is to set up a continuous task to asynchronously receive data, and call a “
handler function ” every time a new piece of data comes in:
Software Engineering & Platform Updates
I've talked about lots of new functions and new functionality in the Wolfram Language. But what about the underlying infrastructure of the Wolfram Language? Well, we've been working hard on that too. For example, between Version 11.3 and Version 12.0 we've managed to fix nearly 8000 reported bugs. We've also made lots of things faster and more robust. And in general we've been tightening the software engineering of the system, for example reducing the initial download size by nearly 10% (despite all the functionality that's been added). (We've also done things like improve the predictive
prefetching of knowledgebase elements from the cloud—so when you need similar data it's more likely to be already cached on your computer.)
It's a longstanding feature of the computing landscape that operating systems are continually getting updated—and to take advantage of their latest features, applications have to get updated too. We've been working for several years on a major update to our Mac notebook interface—which is finally ready in Version 12.0. As part of the update, we've rewritten and restructured large amounts of code that have been developed and polished over more than 20 years, but the result is that in Version 12.0, everything about our system on the Mac is fully 64-bit, and makes use of the latest
Cocoa APIs . This means that the notebook front end is significantly faster—and can also go beyond the previous 2 GB memory limit.
There's also a platform update on Linux, where now the notebook interface fully supports
Qt 5 , which allows all rendering operations to take place “headlessly”, without any X server—greatly streamlining deployment of the
Wolfram Engine in the cloud. (Version 12.0 doesn't yet have high-dpi support for Windows, but that's coming very soon.)
The development of the
Wolfram Cloud is in some ways separate from the development of the Wolfram Language, and
Wolfram Desktop applications (though for internal compatibility we're releasing Version 12.0 at the same time in both environments). But in the past year since Version 11.3 was released, there's been dramatic progress in the Wolfram Cloud.
Especially notable are the advances in cloud notebooks—supporting more interface elements (including some, like embedded websites and videos, that aren't even yet available in desktop notebooks), as well as greatly increased robustness and speed. (Making our whole notebook interface work in a web browser is no small feat of software engineering, and in Version 12.0 there are some pretty sophisticated strategies for things like maintaining consistent fast-to-load caches, along with full symbolic DOM representations.)
In Version 12.0 there's now just a simple menu item (File > Publish to Cloud …) to publish any notebook to the cloud. And once the notebook is published, anyone in the world can interact with it—as well as make their own copy so they can edit it.
It's interesting to see
how broadly the cloud has entered what can be done in the Wolfram Language. In addition to all the seamless integration of the cloud knowledgebase, and the ability to reach out to things like blockchains, there are also conveniences like
Send To … sending any notebook through email, using the cloud if there's no direct email server connection available.
And a Lot Else…
Even though this has been a long piece, it's not even close to telling the whole story of what's new in Version 12.0. Along with the rest of our team, I've been working very hard on Version 12.0 for a long time now—but it's still exciting to see just how much is actually in it.
But what's critical (and a lot of work to achieve!) is that everything we've added is carefully designed to fit coherently with what's already there. From the very first version more than 30 years ago of what's now the Wolfram Language, we've been following the same core principles—and this is part of what's allowed us to so dramatically grow the system while maintaining long-term compatibility.
It's always difficult to decide exactly what to prioritize developing for each new version, but I'm very pleased with the choices we made for Version 12.0. I've given many talks over the past year, and I've been very struck with how often I've been able to say about things that come up: “Well, it so happens that that's going to be part of Version 12.0!”
I've personally been using internal preliminary builds of Version 12.0 for nearly a year, and I've come to take for granted many of its new capabilities—and to use and enjoy them a lot. So it's a great pleasure that today we have the final Version 12.0—with all these new capabilities officially in it, ready to be used by anyone and everyone…