Introduccion
Este artículo es una continuación de una
serie de artículos que describen los algoritmos subyacentes.
Synet es un marco para lanzar redes neuronales pre-entrenadas en la CPU.
Si observa la distribución del tiempo del procesador que se dedica a la propagación directa de la señal en las redes neuronales, resulta que a menudo más del 90% de todo el tiempo se gasta en capas convolucionales. Por lo tanto, si queremos obtener un algoritmo rápido para una red neuronal, necesitamos, en primer lugar, un algoritmo rápido para una capa convolucional. En este artículo, quiero describir métodos para optimizar la propagación de señal directa en una capa convolucional. Y quiero comenzar con los métodos más utilizados basados en la multiplicación de matrices. Trataré de mantener la presentación en la forma más accesible para que el artículo sea interesante no solo para los especialistas (ya lo saben todo), sino también para un círculo más amplio de lectores. No pretendo ser una revisión completa, por lo que cualquier comentario y adición son bienvenidos.
Opciones de capa de convolución
Me gustaría comenzar la descripción con una descripción de los parámetros que están en la capa convolucional. Los expertos pueden saltarse esta sección de manera segura.
Tamaños de imagen de entrada y salida
En primer lugar, una capa convolucional se caracteriza por una imagen de entrada y una imagen de salida, que se caracterizan por los siguientes parámetros:

- srcC / dstC : el número de canales en la imagen de entrada y salida. Notación alternativa: C / D.
- srcH / dstH : altura de la imagen de entrada y salida. Designación alternativa: H.
- srcW / dstW : ancho de la imagen de entrada y salida. Designación alternativa: W.
- lote : la cantidad de imágenes de entrada (salida): la capa puede procesar un lote completo de imágenes a la vez. Designación alternativa: N.
Tamaños centrales de convolución
La operación de convolución es inherentemente una suma ponderada de cierto vecindario de un punto dado en la imagen. El tamaño del núcleo de convolución: caracteriza el tamaño de este vecindario y se describe mediante dos parámetros:

- kernelY es la altura del kernel de convolución. Designación alternativa: Y.
- kernelX es el ancho del núcleo de convolución. Designación alternativa: X.
Las convoluciones más comunes con un tamaño de núcleo de
1x1 y
3x3 . Los tamaños
5x5 y
7x7 son mucho menos comunes. A veces también se encuentran grandes tamaños de convolución, así como convoluciones con un núcleo que no sea cuadrado, pero esto es más exótico.
Paso de convolución
Otro parámetro importante es el paso de convolución:

- zancada es el paso de convolución vertical.
- strideX - paso de convolución horizontal.
Si el paso es diferente de
1x1 , por ejemplo,
2x2 , la imagen de salida será la mitad (la convolución se calculará solo en la vecindad de los puntos pares).
Convolución de estiramiento
El núcleo de convolución se puede estirar (aumentar el tamaño efectivo de la ventana, mientras se mantiene el número de operaciones) utilizando los siguientes parámetros:
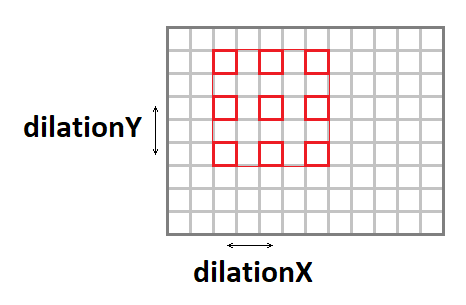
- dilatación Y : estiramiento vertical de la convolución.
- dilatación X : estiramiento horizontal de la convolución.
Vale la pena señalar que los casos de estiramiento que no sean
1x1 son bastante raros (nunca he encontrado algo así en mi carrera).
Imagen de entrada de relleno
Si aplica una convolución con una ventana que es diferente de una sola a la imagen, entonces la imagen de salida será menor en la cantidad de
kernel - 1 . El paquete, por así decirlo, "se come" los bordes. Para preservar el tamaño de la imagen, la imagen de entrada a menudo se rellena alrededor de los bordes con ceros. Cuatro parámetros más son responsables de esto:

- padY / padX - acolchado frontal vertical y horizontal.
- padH / padW - acolchado trasero vertical y horizontal.
Grupos de canales
Típicamente, cada canal de salida es la suma de las convoluciones en todos los canales de entrada. Sin embargo, este no es siempre el caso. Es posible dividir los canales de entrada y salida en grupos, la suma se lleva a cabo solo dentro de los grupos:

- grupo : el número de grupos.
En la práctica, las situaciones con
group = 1 y
group = srcC = dstC , la llamada
convolución profunda, se encuentran con mayor frecuencia.
Desplazamiento y función de activación
Aunque formalmente el desplazamiento y la función de activación no están incluidos en la convolución, con mucha frecuencia estas dos operaciones siguen la capa convolucional, por lo que generalmente también se incluyen en ella. En vista de la variedad de posibles funciones de activación y sus parámetros, no las describiré aquí en detalle.
Implementación básica del algoritmo.
Para empezar, me gustaría dar una implementación básica del algoritmo:
float relu(float value) { return value > 0 ? return value : 0; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int b = 0; b < batch; ++b) { for (int g = 0; g < group; ++g) { for (int dc = 0; dc < dstC / group; ++dc) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { float sum = 0; for (int sc = 0; sc < srcC / group; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) sum += src[((b * srcC + sc)*srcH + sy)*srcW + sx] * weight[((dc * srcC / group + sc)*kernelY + ky)*kernelX + kx]; } } } dst[((b * dstC + dc)*dstH + dy)*dstW + dx] = relu(sum + bias[dc]); } } } } } }
En esta implementación, asumí que la imagen de entrada y salida está en formato
NCHW :
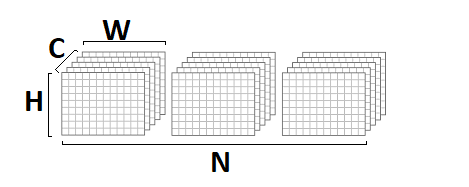
los pesos de convolución se almacenan en formato
DCYX , y nuestra función de activación es
ReLU . En el caso general, esto no es así, pero para la implementación básica, tales suposiciones son bastante apropiadas: debe comenzar desde algo.
Tenemos 8 ciclos anidados y el número total de operaciones:
batch * kernelY * kernelX * srcC * dstH * dstW * dstC / group * 2,
mientras que la cantidad de datos en la entrada:
batch * srcC * srcH * srcW,
y la imagen de salida:
batch * dstC * dstH * dstW,
y la cantidad de pesos:
kernelY * kernelX * srcC * dstC / group.
Si el
grupo << srcC (el número de grupos es mucho menor que el número de canales), así como con parámetros suficientemente grandes
srcC ,
srcH ,
srcW y
dstC , obtenemos un problema informático clásico cuando el número de cálculos excede significativamente la cantidad de datos de entrada y salida. Es decir La operación de convolución con una implementación adecuada debe descansar en los recursos informáticos del procesador y no en el ancho de banda de la memoria. Solo queda encontrar esta implementación.
Reducción del problema a la multiplicación de matrices.
La operación principal en la convolución es obtener una suma ponderada, y los pesos son los mismos para todos los puntos de la imagen de salida. Si reorganiza la imagen de entrada de la siguiente manera:
void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int sc = 0; sc < srcC; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[((b * srcC + sc)*srcH + sy)*srcW + sx]; else *buf++ = 0; } } } } } }
Luego
cambiaremos del formato
srcC - srcH - srcW y
cambiaremos al formato
srcC - kernelY - kernelX - dstH - dstW . La figura siguiente muestra cómo se convierte la imagen con relleno
1 y núcleo
3x3 :
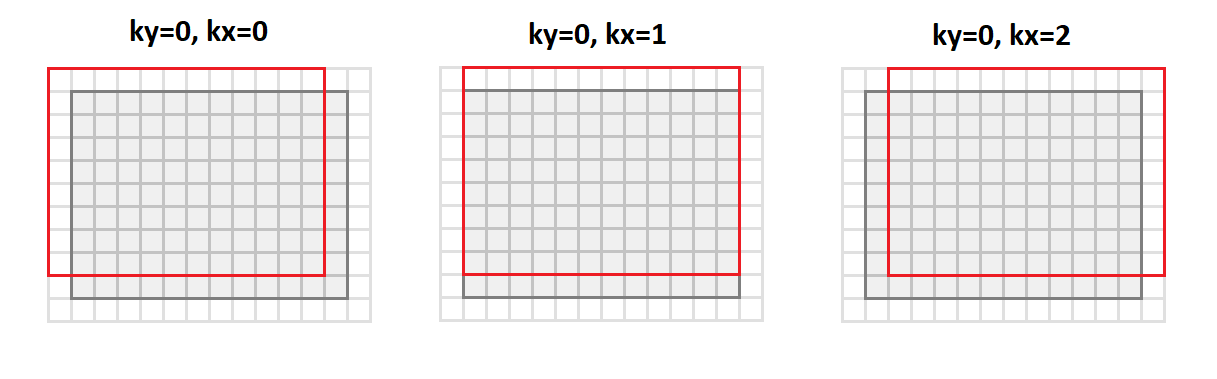
En este caso, todos los puntos de la vecindad de la imagen que se requieren para la operación de convolución se alinean a lo largo de las columnas de la matriz resultante (de ahí su nombre, es decir, las columnas).
La nueva representación de la imagen de entrada es interesante porque ahora la operación de convolución en nosotros se reduce a la multiplicación de matrices:
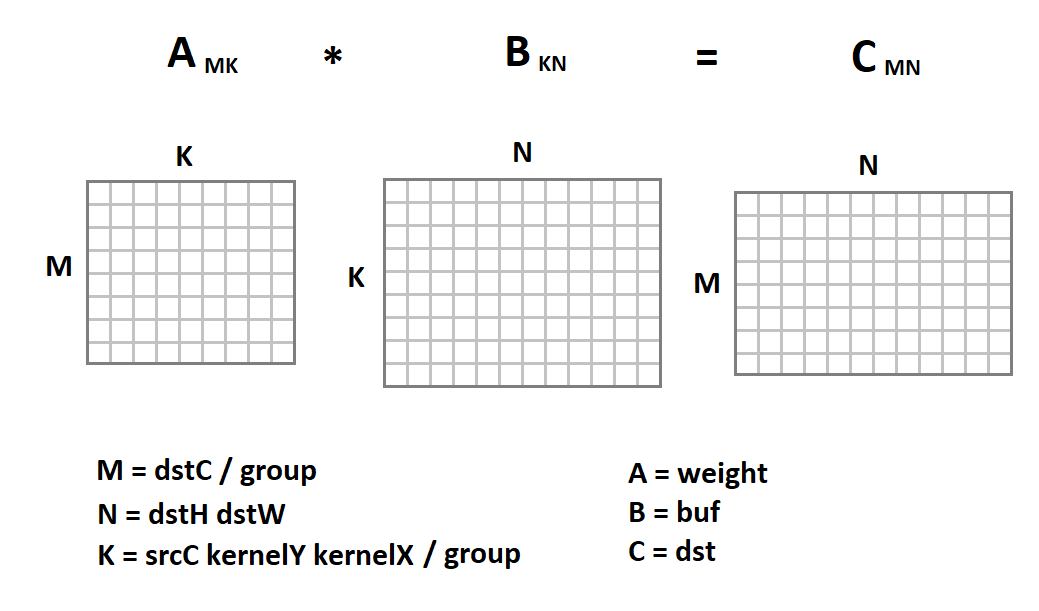
Ahora el código de convolución se verá así:
void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) { for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstC / group; int N = dstH * dstW; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, weight + M * K * g, K, 0, buf + N * K * g, N, dst + M * N * g, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } }
Aquí la implementación trivial de la multiplicación de matrices se da solo como un ejemplo. Podemos reemplazarlo con cualquier otra implementación. Afortunadamente, la multiplicación de matrices es una operación establecida desde hace mucho tiempo que ya se ha implementado en muchas bibliotecas con una eficiencia muy alta (hasta el 90% del rendimiento de CPU teóricamente posible). Sobre el tema de cómo se logra esta eficiencia, incluso tengo un
artículo separado .
Usando la multiplicación de matrices para el formato NHWC
Junto con el formato
NCHW ,
NHWC se usa a menudo en el aprendizaje automático:

Como ejemplo, tenga en cuenta que
NHWC es el formato nativo de
Tensorflow .
Es de destacar que para este formato, la operación de convolución también puede conducir a la multiplicación de matrices. Para hacer esto, desde el formato
srcH - srcW - srcC traducimos la imagen original al formato
dstH - dstW - kernelY - kernelX - srcC usando la función
im2row :
void im2row(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int g = 0; g < group; ++g) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; for (int sc = 0; sc < srcC; ++sc) { if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[(sy * srcW + sx)*srcC + sc]; else *buf++ = 0; } } } } } src += srcC / group; } }
Además, todos los puntos de la vecindad de la imagen que se requieren para la operación de convolución se alinean a lo largo de las filas de la matriz resultante (de ahí su nombre - imagen
a la fila s). También debemos cambiar el formato de almacenamiento de las escalas de convolución del formato
DCYX al formato
YXCD . Ahora podemos aplicar la multiplicación de matrices:

A diferencia del formato
NCHW , multiplicamos la matriz de imagen por la matriz de peso, y no al revés. El siguiente es un código de función de convolución:
void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstH * dstW; int N = dstC / group; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2row(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, group, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, buf + M * K * g, K * group, 0, weight + N * g, dstC, dst + N * g, dstC)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } }
Ventajas y desventajas del método.
Desde el principio, me gustaría enumerar las ventajas de este enfoque:
- Este método tiene una implementación muy simple. No en vano, se usa en casi todas las bibliotecas que conozco.
- La efectividad del método para muchos casos es muy alta: desde unidades de porcentaje en la versión básica alcanzamos más del 80% del máximo teórico.
- El enfoque es universal: tenemos un código para todos los parámetros posibles de la capa convolucional (¡y hay muchos de ellos!). Por lo tanto, este método a menudo funciona en casos donde los enfoques más efectivos (y por lo tanto más especializados) tienen limitaciones.
- El enfoque funciona para los principales formatos de tensores de imagen: NCHW y NHWC .
Ahora sobre las desventajas:
- Desafortunadamente, la multiplicación matricial estándar es efectiva siempre que los valores de los parámetros M, N, K sean lo suficientemente grandes y, además, tengan aproximadamente el mismo orden de magnitud (la eficiencia se basa en el hecho de que el número requerido de cálculos es ~ O (N ^ 3) y el rendimiento requerido capacidad de memoria ~ O (N ^ 2) ). Por lo tanto, si alguno de los parámetros M, N, K es pequeño, la eficiencia del método cae bruscamente.
- El método requiere la conversión de datos de entrada. Y esto está lejos de ser una operación gratuita. Solo puede ser descuidada si K es lo suficientemente grande. Y si tenemos en cuenta que dentro de la multiplicación de matriz estándar todavía hay una transformación interna de los datos de entrada, entonces la situación se vuelve aún más triste.
- Basado en el hecho de que K = srcC * kernelY * kernelX / group , la eficiencia del método es especialmente baja para las capas convolucionales de entrada. Y para una convolución profunda, el método de la matriz generalmente pierde con la implementación trivial.
- El método requiere un procesamiento adicional de los datos de salida para la operación de cambio y el cálculo de la función de activación.
- Existen métodos matemáticos más eficientes para calcular la convolución, que requieren menos operaciones.
Conclusiones
El método de cálculo de convolución basado en la multiplicación de matrices es simple de implementar y tiene una alta eficiencia. Lamentablemente, no es universal. Para una serie de casos especiales, hay enfoques más rápidos, cuya descripción me gustaría posponer para los próximos artículos de esta
serie . Esperando comentarios y comentarios de los lectores. ¡Espero que te haya interesado!
PD: Este y otros enfoques son implementados por mí en el
Marco de Convolución como parte de la biblioteca
Simd .
Este marco subyace a
Synet , un marco para ejecutar redes neuronales pre-entrenadas en la CPU.