Prólogo
No hace mucho tiempo tuve que trabajar para simplificar la cadena poligonal (un
proceso que permite reducir la cantidad de puntos de polilínea ). En general, este tipo de tarea es muy común al procesar gráficos vectoriales y al construir mapas. Como ejemplo, podemos tomar una cadena cuyos varios puntos caen en el mismo píxel; es obvio que todos estos puntos se pueden simplificar en uno. Hace algún tiempo, prácticamente no sabía nada de esto por la palabra "completamente", y por lo tanto, tuve que llenar rápidamente los conocimientos necesarios sobre este tema. Pero cuál fue mi sorpresa cuando no encontré suficientes manuales completos en Internet en Internet ... Tuve que buscar fragmentos de información de fuentes completamente diferentes y, después del análisis, construir todo en una imagen general. La ocupación no es una de las más agradables, para ser honesto. Por lo tanto, me gustaría escribir una serie de artículos sobre algoritmos de simplificación de cadena poligonal. Simplemente decidí comenzar con el algoritmo Douglas-Pecker más popular.
Descripción
El algoritmo establece la polilínea inicial y la distancia máxima (ε), que puede estar entre las polilíneas originales y simplificadas (es decir, la distancia máxima desde los puntos del original hasta la sección más cercana de la polilínea resultante). El algoritmo divide recursivamente la polilínea. La entrada al algoritmo son las coordenadas de todos los puntos entre el primero y el último, incluidos ellos, así como el valor de ε. El primer y último punto se mantienen sin cambios. Después de eso, el algoritmo encuentra el punto más alejado del segmento que consiste en el primero y el último (
el algoritmo de búsqueda es la distancia desde el punto al segmento ). Si el punto se encuentra a una distancia inferior a ε, entonces todos los puntos que aún no se han marcado para su preservación se pueden expulsar del conjunto, y la línea recta resultante suaviza la curva con una precisión de al menos ε. Si esta distancia es mayor que ε, entonces el algoritmo se llama a sí mismo recursivamente en el conjunto desde el punto inicial hasta el punto dado y desde el punto dado hasta el final.
Vale la pena señalar que el algoritmo Douglas-Pecker no conserva la topología en el curso de su trabajo. Esto significa que, como resultado, podemos obtener una línea con auto intersecciones. Como ejemplo ilustrativo, tome una polilínea con el siguiente conjunto de puntos: [{1; 5}, {2; 3}, {5; 1}, {6; 4}, {9; 6}, {11; 4}, {13; 3}, {14; 2}, {18; 5}] y observe el proceso de simplificación para diferentes valores de ε:
La polilínea original del conjunto de puntos presentado:

Polilínea con ε igual a 0.5:
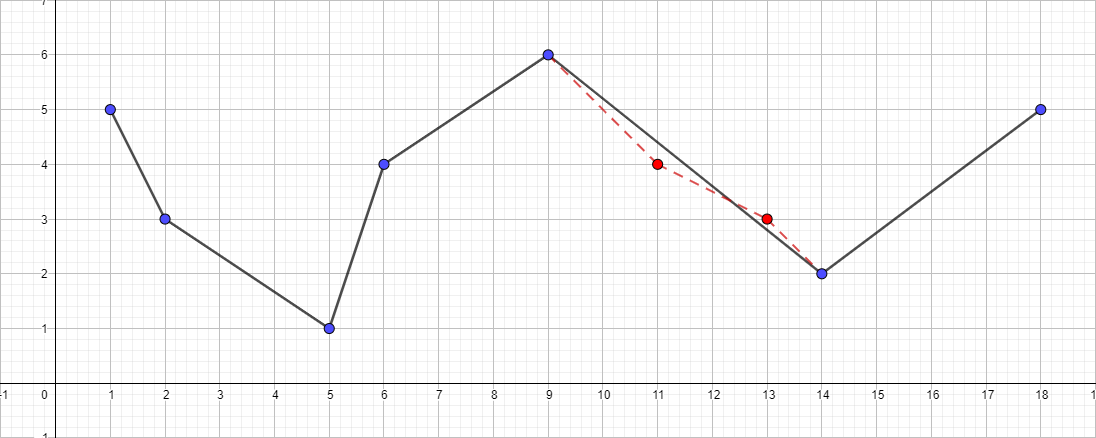
Una polilínea con ε igual a 1:

Polilínea con ε igual a 1.5:
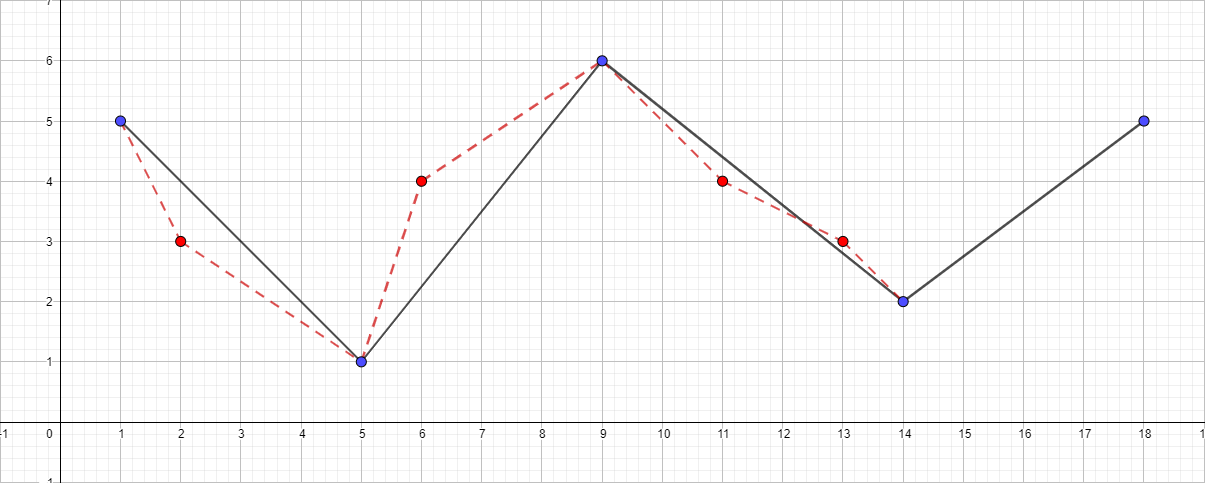
Puede continuar aumentando la distancia máxima y visualizar el algoritmo, pero creo que el punto principal después de estos ejemplos ha quedado claro.
Implementación
C ++ fue elegido como el lenguaje de programación para la implementación del algoritmo, el código fuente completo del algoritmo se puede ver
aquí . Y ahora directamente a la implementación en sí:
#define X_COORDINATE 0 #define Y_COORDINATE 1 template<typename T> using point_t = std::pair<T, T>; template<typename T> using line_segment_t = std::pair<point_t<T>, point_t<T>>; template<typename T> using points_t = std::vector<point_t<T>>; template<typename CoordinateType> double get_distance_between_point_and_line_segment(const line_segment_t<CoordinateType>& line_segment, const point_t<CoordinateType>& point) noexcept { const CoordinateType x = std::get<X_COORDINATE>(point); const CoordinateType y = std::get<Y_COORDINATE>(point); const CoordinateType x1 = std::get<X_COORDINATE>(line_segment.first); const CoordinateType y1 = std::get<Y_COORDINATE>(line_segment.first); const CoordinateType x2 = std::get<X_COORDINATE>(line_segment.second); const CoordinateType y2 = std::get<Y_COORDINATE>(line_segment.second); const double double_area = abs((y2-y1)*x - (x2-x1)*y + x2*y1 - y2*x1); const double line_segment_length = sqrt(pow((x2-x1), 2) + pow((y2-y1), 2)); if (line_segment_length != 0.0) return double_area / line_segment_length; else return 0.0; } template<typename CoordinateType> void simplify_points(const points_t<CoordinateType>& src_points, points_t<CoordinateType>& dest_points, double tolerance, std::size_t begin, std::size_t end) { if (begin + 1 == end) return; double max_distance = -1.0; std::size_t max_index = 0; for (std::size_t i = begin + 1; i < end; i++) { const point_t<CoordinateType>& cur_point = src_points.at(i); const point_t<CoordinateType>& start_point = src_points.at(begin); const point_t<CoordinateType>& end_point = src_points.at(end); const double distance = get_distance_between_point_and_line_segment({ start_point, end_point }, cur_point); if (distance > max_distance) { max_distance = distance; max_index = i; } } if (max_distance > tolerance) { simplify_points(src_points, dest_points, tolerance, begin, max_index); dest_points.push_back(src_points.at(max_index)); simplify_points(src_points, dest_points, tolerance, max_index, end); } } template< typename CoordinateType, typename = std::enable_if<std::is_integral<CoordinateType>::value || std::is_floating_point<CoordinateType>::value>::type> points_t<CoordinateType> duglas_peucker(const points_t<CoordinateType>& src_points, double tolerance) noexcept { if (tolerance <= 0) return src_points; points_t<CoordinateType> dest_points{}; dest_points.push_back(src_points.front()); simplify_points(src_points, dest_points, tolerance, 0, src_points.size() - 1); dest_points.push_back(src_points.back()); return dest_points; }
Bueno, en realidad el uso del algoritmo en sí mismo:
int main() { points_t<int> source_points{ { 1, 5 }, { 2, 3 }, { 5, 1 }, { 6, 4 }, { 9, 6 }, { 11, 4 }, { 13, 3 }, { 14, 2 }, { 18, 5 } }; points_t<int> simplify_points = duglas_peucker(source_points, 1); return EXIT_SUCCESS; }
Ejemplo de ejecución de algoritmo
Como entrada, tomamos un conjunto de puntos conocido anteriormente [{1; 5}, {2; 3}, {5; 1}, {6; 4}, {9; 6}, {11; 4}, {13; 3}, {14; 2}, {18; 5}] y ε igual a 1:
- Encuentre el punto más alejado del segmento {1; 5} - {18; 5}, este punto será el punto {5; 1}.
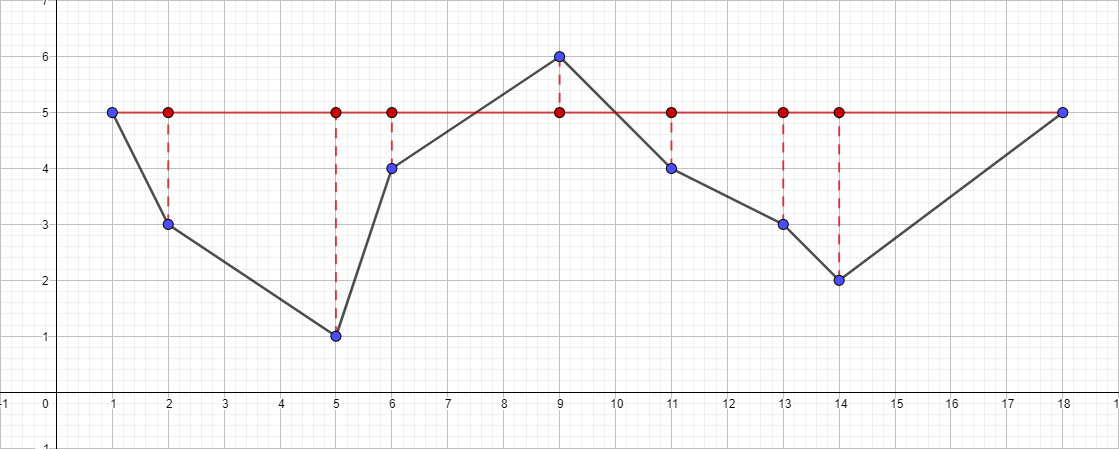
- Verifique su distancia al segmento {1; 5} - {18; 5}. Resulta ser más de 1, lo que significa que lo agregamos a la polilínea resultante.
- Ejecute recursivamente el algoritmo para el segmento {1; 5} - {5; 1} y encuentre el punto más distante para este segmento. Este punto es {2; 3}.
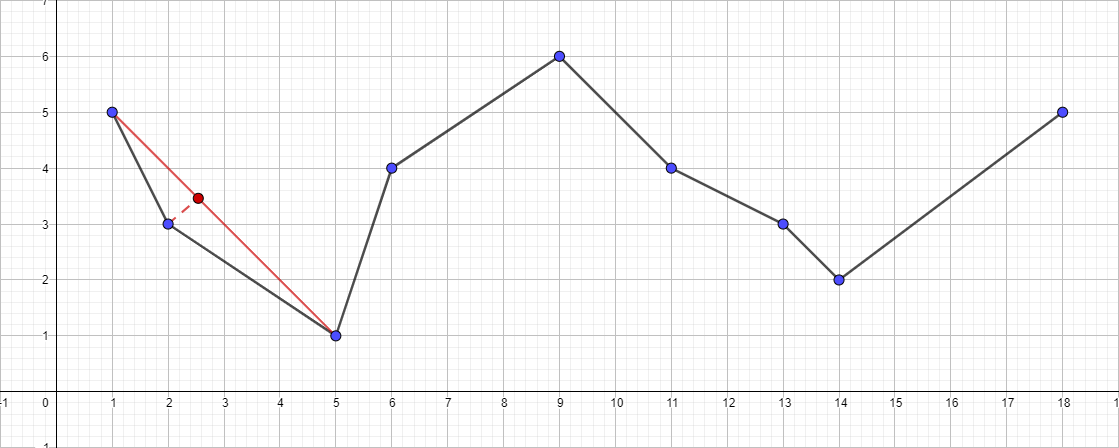
- Verifique su distancia al segmento {1; 5} - {5; 1}. En este caso, es menor que 1, lo que significa que podemos descartar este punto de forma segura.
- Ejecute recursivamente el algoritmo para el segmento {5; 1} - {18; 5} y encuentre el punto más distante para este segmento ...
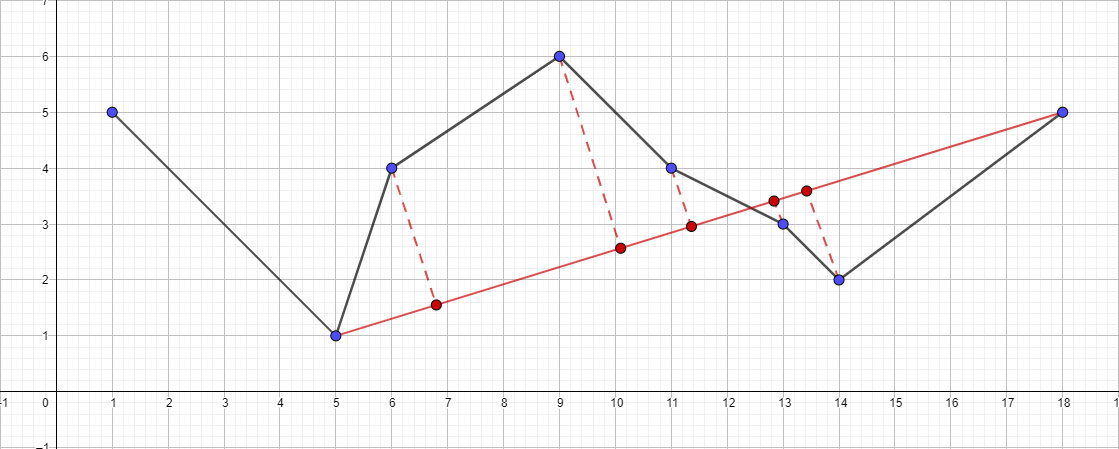
- Y así sucesivamente según el mismo plan ...
Como resultado, el árbol de llamadas recursivas para estos datos de prueba se verá así:
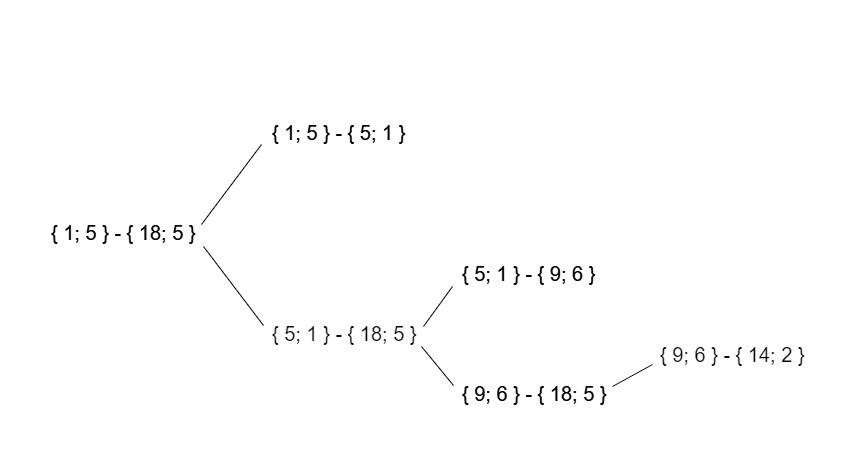
Tiempo de trabajo
La complejidad esperada del algoritmo en el mejor de los casos es O (nlogn), esto es cuando el número del punto más distante siempre es lexicográficamente central. Sin embargo, en el peor de los casos, la complejidad del algoritmo es O (n ^ 2). Esto se logra, por ejemplo, si el número del punto más distante siempre es adyacente al número del punto límite.
Espero que mi artículo sea útil para alguien, también me gustaría llamar la atención sobre el hecho de que si el artículo muestra suficiente interés entre los lectores, pronto estaré listo para considerar algoritmos para simplificar la cadena poligonal de Reumman-Witkam, Opheim y Lang. Gracias por su atencion!