Cuando se analizan series de tiempo estacionarias obtenidas experimentalmente, como regla, durante la preparación preliminar (preprocesamiento) de datos, se hace necesario suprimir la tendencia existente en ellos.
Aquí se propondrá un "nuevo" método de resaltado de tendencias: simple, obvio y adecuado para tipos de tendencias muy complejos.
Una tendencia generalmente se entiende como un componente no armónico de frecuencia ultrabaja que viola la estacionariedad del proceso. La causa más común de una tendencia en los datos obtenidos experimentalmente es la "deriva cero" del equipo de grabación. La integración de datos y algunos otros tipos de procesamiento también pueden causar una tendencia. La presencia de una tendencia distorsiona en gran medida los resultados del procesamiento posterior de datos (estimación espectral, etc.), por lo tanto, la eliminación de la tendencia es necesaria. En algunos casos, la tendencia en sí misma es una fuente valiosa de información (por ejemplo, al analizar tendencias a largo plazo en procesos económicos o meteorológicos).
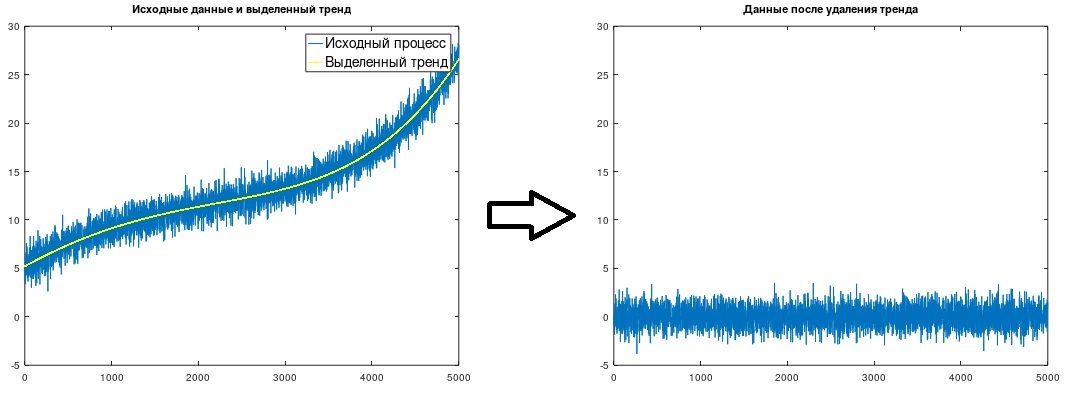Fig. 1. Aislamiento y eliminación de una tendencia.Por lo general, una tendencia se modela utilizando funciones lineales o de potencia (segundo o tercer orden), cuyos coeficientes se calculan multiplicando el proceso por ciertas secuencias y luego aplicando fórmulas bastante complejas derivadas del método de mínimos cuadrados. (véase, por ejemplo, J. Bendat, A. Pirsol, "Análisis aplicado de datos aleatorios", M., Mir, 1989.) El siguiente es un método ligeramente modificado, también basado en el método de mínimos cuadrados, que es muy fácil de entender y aprender, y no requiere referencia a directorios, ni cálculos simbólicos complejos independientes para obtener las dependencias necesarias, mientras le permite modelar la tendencia con funciones de cualquier tipo. Este método modificado es tan simple y obvio (una vez dominado, los scripts se pueden escribir de la memoria) que probablemente haya sido "inventado" por diferentes investigadores más de una vez, pero todavía no he encontrado nada en ninguna de las fuentes.
Para resaltar la tendencia, se realiza una aproximación del proceso inicial x [i], que consiste en N + 1 muestras, utilizando un pequeño número de k funciones que conforman la tendencia u
j [i]:
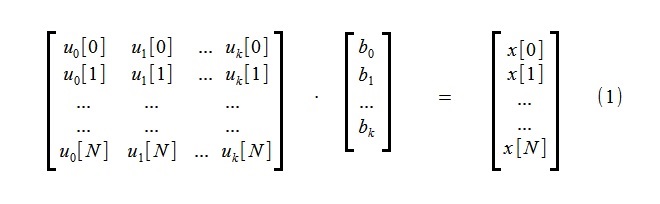
(Por lo general, las funciones de potencia se eligen como funciones u
j [i],
pero para este método es absolutamente sin principios)
El sistema de ecuaciones algebraicas lineales (1) incluye k ecuaciones desconocidas b
j y N + 1.
Tomando la notación:
escribe más compacto
La aplicación del método de mínimos cuadrados en la búsqueda de una solución aproximada de un sistema sobredeterminado se escribe en forma de matriz de la siguiente manera:
Al escribir un guión: Naturalmente, no es necesario almacenar toda la matriz grande U, los elementos de la matriz U
T U y el vector U
T x se pueden "acumular" paso a paso.
El sistema (4) de k ecuaciones yk incógnitas se resuelve por métodos obvios; bueno, por ejemplo, lo escribimos así:
después de lo cual, utilizando el b
j encontrado, podemos construir la tendencia θ [i] en la forma
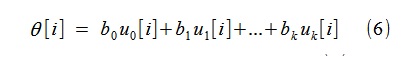
Por ejemplo, se simuló un proceso aleatorio x [i] del formulario
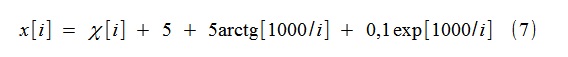
donde χ [i] - ruido blanco gaussiano con una sola dispersión. La tendencia está modelada por funciones del tipo (2) (más precisamente, (8)), hasta 4º orden (k = 4) inclusive.
Cuando se utilizan funciones de ley de potencia para el modelado de tendencias, debe tenerse en cuenta que la matriz U
T U (4) es teóricamente siempre reversible debido a la independencia lineal de estas funciones, sin embargo, en órdenes altas de k (o realizaciones muy largas de N, lo que es menos crítico), algunos de sus elementos pueden ser muy genial en valor absoluto. En órdenes altas de k, en caso de dificultades computacionales, se recomienda utilizar coeficientes reductores, por ejemplo, (8):
(Δt = 1), que se realizó en el ejemplo considerado. Se obtiene la tendencia que se muestra en la Fig. 1.
Después de resaltar una tendencia, naturalmente, simplemente se debe restar de los datos de origen.
Observación Por lo general, las fuentes autorizadas no recomiendan trabajar con modelos de tendencia del orden superior a k = 2 (parábola cuadrada). No está muy claro si esto se debe a la dificultad de determinar los coeficientes de "amplitud" b
j por métodos tradicionales, o al agotamiento de los órdenes de las variables de máquina mencionadas anteriormente, o la asignación falsa de componentes informativos del proceso a la tendencia. En el ejemplo dado, la tendencia de 4º orden se resalta como si fuera bastante plausible (aunque no muy diferente de la tendencia de 3er orden). Para casos particularmente difíciles, las fuentes recomiendan usar un método diferente: filtrado de paso bajo (no considerado aquí).
Al resaltar una tendencia, como se muestra arriba, el procedimiento no es tan complicado, le permite seleccionar y analizar tendencias "lentas" o, más a menudo, ayuda a obtener datos de alta calidad, un proceso aleatorio estacionario centrado adecuado para un análisis posterior.