
Introduccion
Este artículo describe los resultados de un experimento realizado en el marco del proyecto "Tipo de cambio absoluto". El protocolo experimental se puede ver haciendo clic en el enlace .
El proyecto " Tipo de cambio absoluto " se dedica al análisis de los tipos de cambio emparejados, la asignación de los tipos de cambio absolutos de ellos y su análisis. En el marco del proyecto, se obtuvo una metodología para la conversión de tasas de pares a tasas de cambio absolutas. Para esto, se define la moneda absoluta ABS. Todas las monedas disponibles se expresan en términos de ABS.
En el artículo " De pares de divisas a tipos de cambio absolutos " se ofrece una descripción detallada de la tecnología.
Hasta la fecha, ya se han publicado varios artículos sobre la aplicación del método de tipo de cambio absoluto. Traigo los dos últimos.
El artículo " Un estudio de la conexión de las monedas mundiales a través de la correlación de los tipos de cambio absolutos " describe una de las aplicaciones de la tecnología de los tipos de cambio absolutos. Se da un método formal para calcular la relación entre las diferentes monedas.
El artículo " El método de cartera de Markowitz aplicado al mercado de divisas " describe la tecnología previamente inaccesible para optimizar la cartera de divisas.
A continuación se describe el método de conversión de los tipos de cambio de par (relativos) a absolutos. Se dan los parámetros numéricos de la transformación y la metodología para su cálculo.
En el archivo fuente, los tipos de cambio diarios se cargan automáticamente diariamente y los absolutos se calculan a partir de ellos.
La matriz de transformación se obtuvo en 2017. Se calculó a tipos de cambio de pares reales minimizando el error de desviación de los tipos de pares restaurados del absoluto. Desde entonces, no se ha realizado ningún análisis de errores en los datos modernos.
Los resultados de verificación inesperados descritos a continuación condujeron al desarrollo de una nueva técnica para obtener la matriz de transformación. Además, se detectó un error al procesar las cotizaciones importadas.
Fundamentos teóricos
Para obtener tasas de cambio absolutas, debe realizar la siguiente conversión. Para comenzar, los cursos emparejados son logaritmo. A continuación, los multiplicamos por la matriz de transformación inversa. Al final, regresamos de la escala logarítmica usando un exponente.
Para la transición posterior a los cursos en pareja, se deben registrar los cursos absolutos. Luego multiplique por la matriz de transformación directa. Concluimos como antes usando el exponente.
La tecnología se describe con más detalle en el artículo " De los pares de divisas a las tasas absolutas de las monedas individuales " (solo este artículo de 2018 ofrece una representación transpuesta de las matrices de transformación en contraste con la presentación de este artículo).
La matriz directa se determina fácilmente. Las filas en él corresponden a monedas, y las columnas corresponden a pares de divisas. La matriz es muy escasa y consta de ceros, unos y menos unos.
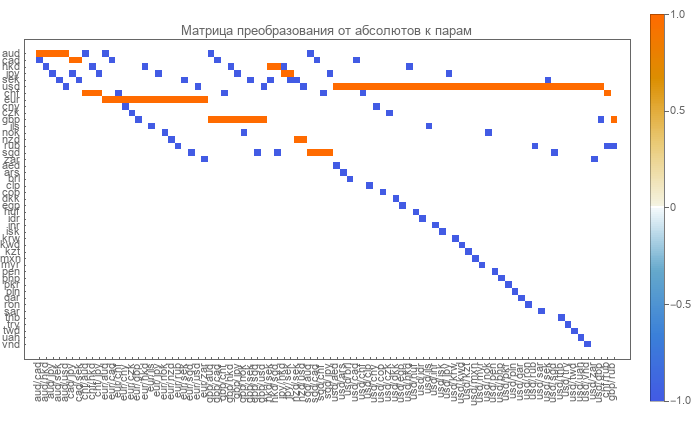
Los ceros indican la ausencia de tal par y moneda. La unidad corresponde a la moneda en el numerador del par. El menos uno indica la moneda en el denominador del par.
La matriz de transformación inversa de pares a tasas absolutas no está definida. Debe ser calculado. El método más obvio es minimizar el error en la recuperación de pares. Lo que se hizo para calcular esta matriz en 2017. Damos una representación gráfica de esta matriz.
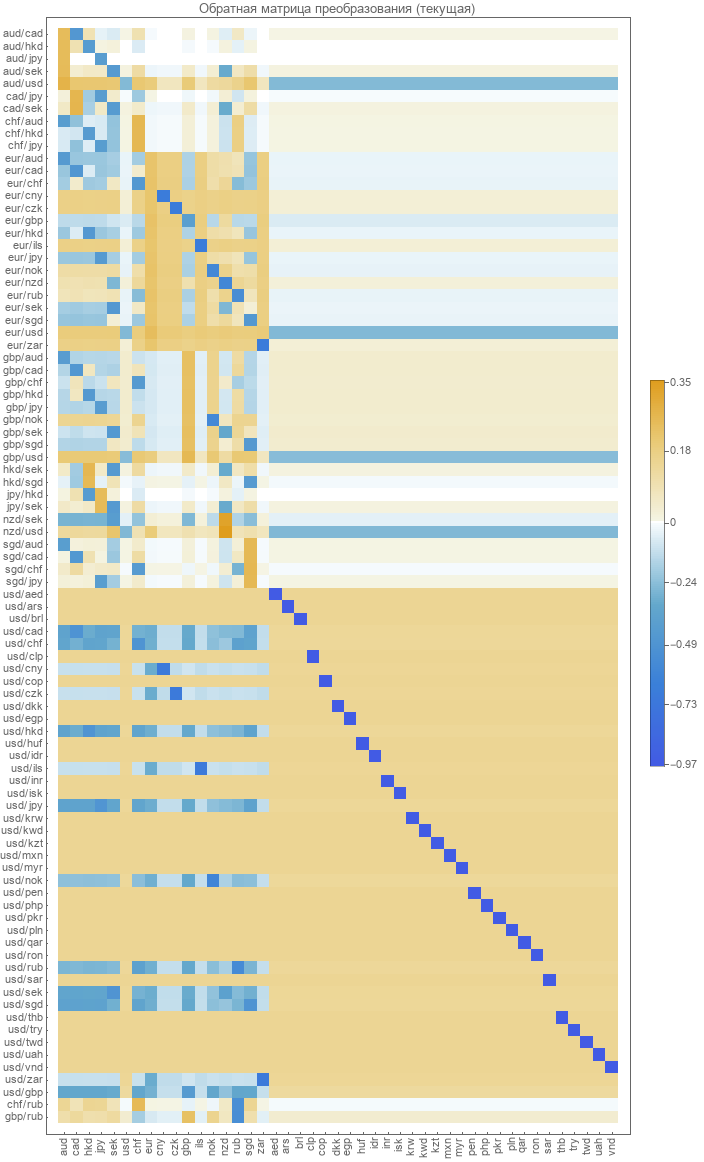
Comprobación de la precisión de un modelo existente
Para la matriz actual, se obtuvieron los tipos de cambio de pares absolutos y restaurados. Hubo fuertes diferencias entre los cursos emparejados originales y restaurados.

A continuación, se realizó el cálculo de los errores de recuperación para todos los pares.
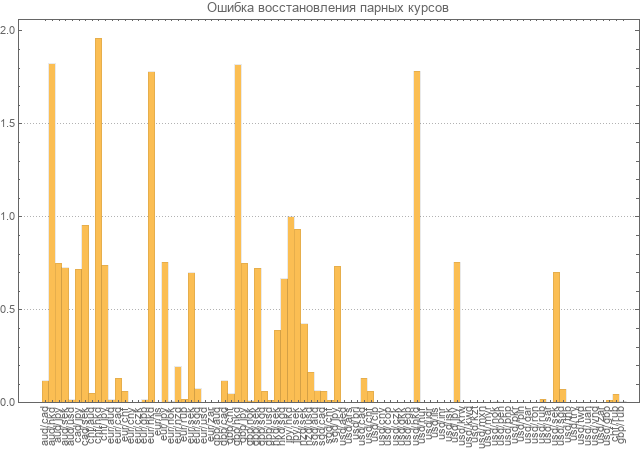
El error se consideró como el promedio de las desviaciones relativas tomadas módulo. Como se puede ver en el diagrama, los errores para muchos pares son casi el doble de los valores mismos.
Por supuesto, este nivel de error no permite que el modelo se considere consistente y requiere un recuento.
Matriz pseudoinversa de una línea
Lo primero que intentaremos es simplemente calcular la matriz inversa para la matriz de transformación directa. Debido al hecho de que la matriz no es cuadrada, tendremos que usar la transformación pseudo-inversa . El resultado tiene lo siguiente.
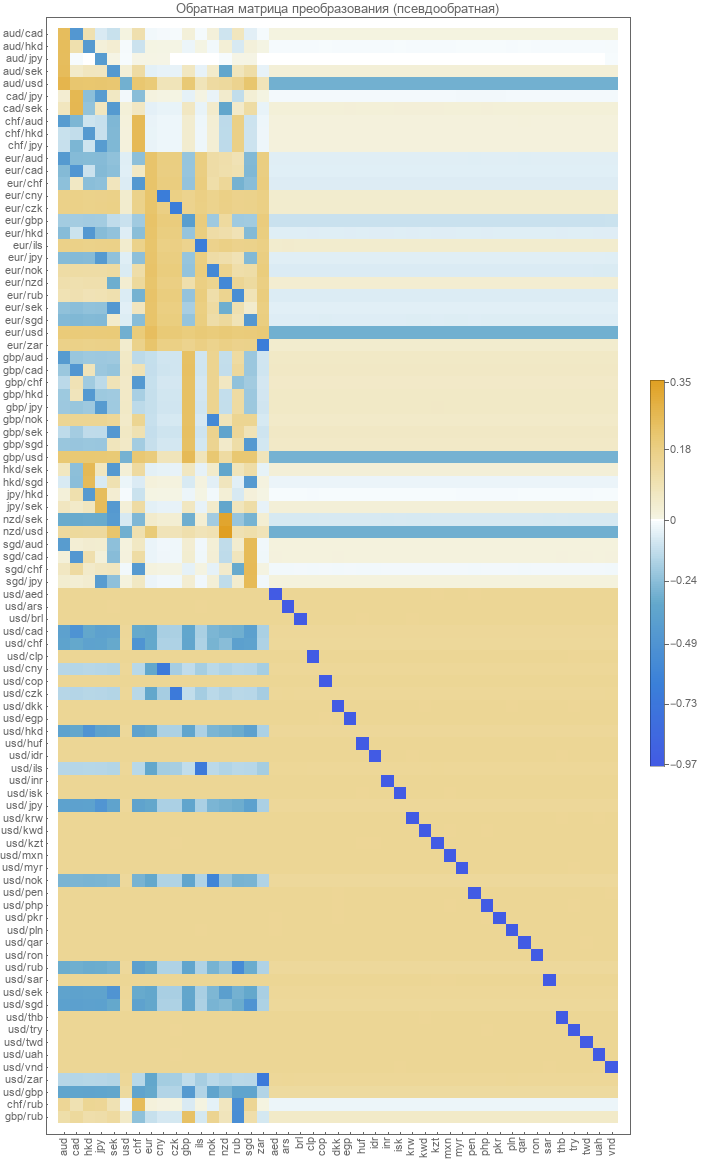
Es muy similar a lo que obtuvimos anteriormente usando tasas de cambio de pares reales para la optimización.
Calculamos cursos absolutos. Luego restaurar desde los cursos de pareja absoluta. La tabla de errores es la siguiente.

Los errores también resultaron ser grandes, como en la evaluación anterior. Este modelo tampoco puede adaptarse a nosotros.
Cálculo de la matriz inversa a través de componentes linealmente independientes
Si analizamos la matriz de transformación directa en detalle, podemos encontrar que tiene una forma degenerada (el rango de la matriz es menor que el número de filas de divisas). En otras palabras, hay filas linealmente dependientes en la matriz directa. Y por lo tanto, no podemos obtener una matriz inversa aceptable.
Para salir de esta situación, se propuso la siguiente solución. En la transición de cursos absolutos a emparejados, primero debe cambiar a componentes linealmente independientes. Y solo entonces pasa a las parejas. Las matrices de transición de cursos absolutos a componentes y de componentes a cursos emparejados serán no degeneradas y se pueden obtener matrices inversas.
Para buscar componentes linealmente independientes, es necesario adjuntar una matriz de unidades de cursos de pares a la matriz de transformación directa. Por lo tanto, obtenemos dos matrices de la transición de cursos absolutos a emparejados y la matriz adjunta de la transición de emparejados a emparejados.

Ahora llevaremos a cabo transformaciones estándar en la forma escalonada de la parte superior de esta matriz combinada (de hecho, las herramientas estándar del paquete matemático Wolfram Mathematica conducen a la forma diagonal ). Como resultado, fue posible obtener la siguiente matriz transformada.

Ahora en las columnas de esta matriz tenemos componentes linealmente independientes. Además, podemos cambiar a ellos tanto desde cursos absolutos (la parte superior de la matriz) como desde cursos emparejados (la parte inferior de la matriz transformada combinada).
Seleccionamos estas matrices de transición a componentes linealmente independientes. Aquí está la matriz de transición para componentes de cursos absolutos.
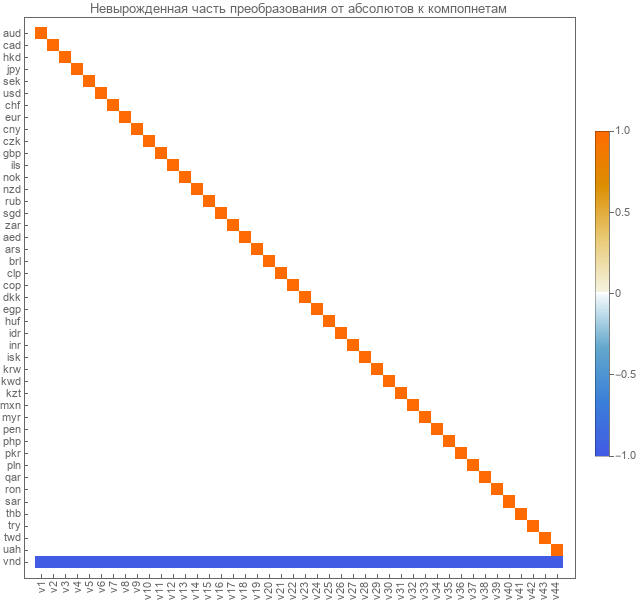
Aquí está la matriz de transición de cursos de pares a componentes linealmente independientes.

La transición de absolutos a componentes ocurre a través de la matriz calculada anteriormente. La transformación inversa de componentes a absolutos se realiza a través de la matriz inversa. Debido al hecho de que no será degenerado, se puede obtener una buena matriz inversa. Recibiremos como pseudo-inverso. Aquí está su punto de vista.

Ahora puede obtener la matriz de transformación inversa completa de pares a absolutos. Para hacer esto, multiplicamos la matriz de transformación de pares a componentes por la matriz de transformación inversa de componentes a absolutos. Ella se ve así.

Aunque ya hemos visto un similar arriba, pero la matriz sigue siendo diferente. Examinamos los resultados que da. Calcularemos cursos absolutos, y de ellos ya restauraremos emparejados. El error de recuperación fue el siguiente.

En todos los pares, excepto dos, casi cero errores. Descubrimos lo que está mal con estos pares.
Resulta que en dos pares de divisas se aceptan los datos incorrectos. Para jpy / hkd y jpy / sek, los datos van en lotes de 10000 y 100 piezas. Es necesario corregir y volver a verificar.
Después de corregir los cursos de pares de entrada (deshacerse de lotes) y volver a calcular los cursos de pares absolutos y restaurados, observamos el error de recuperación.

Tengo un error dentro del 0.3%. Un nivel de error bastante aceptable.
Aquí hay un ejemplo de un gráfico de curso absoluto.
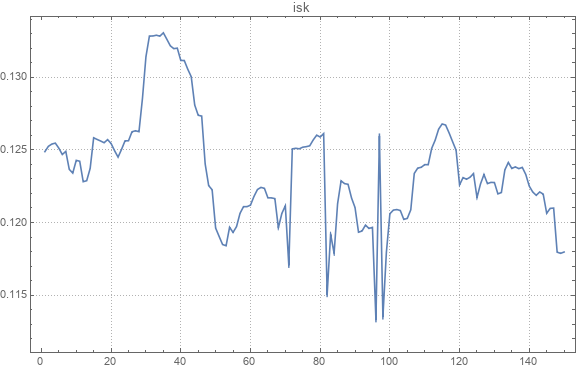
Aquí hay un ejemplo de los tipos de cambio de pares originales y restaurados.

Como hemos recalculado la nueva matriz de la transformación inversa, nuevamente presentamos datos sobre las últimas tasas absolutas de todas las monedas participantes.
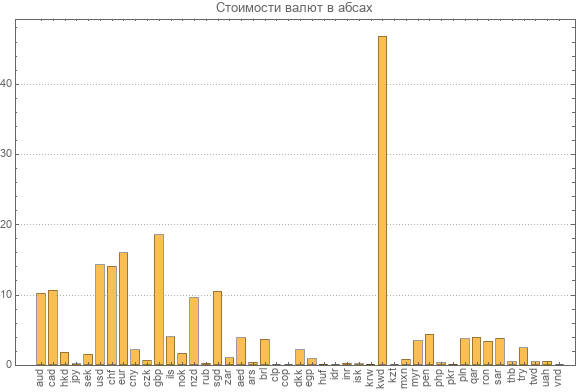
Puedes ver la moneda más cara. Este es un dinar kuwaití que vale casi 47 abdominales. El valor absoluto más pequeño del dong vietnamita es 0.003 abs.
Conclusiones
Como resultado de los estudios, se encontró que el método existente para calcular las tasas absolutas da un error significativo. Además, se detectó un error en los datos de origen.
La matriz de transformación inversa de pares a absolutos solo se obtuvo utilizando el método de transformación a un número menor de componentes linealmente independientes con una matriz de transformación no degenerada.
El método para obtener la matriz de transformación inversa no utilizó datos de velocidad de pares. Y por lo tanto independiente de ellos.
La verificación de la conversión en cursos reales mostró un bajo nivel de error. De lo cual se concluyó que la matriz encontrada de la transformación inversa es aplicable desde los tipos de cambio emparejados a los absolutos.
El método no pretende completarse y verificarse matemáticamente, pero como solución aceptable se utilizará para futuros estudios de sus tipos de cambio absolutos.