Este artículo describe la biblioteca
optlib , diseñada para resolver problemas de optimización global en el lenguaje Rust. En el momento de escribir este artículo, esta biblioteca implementa un algoritmo genético para encontrar el mínimo global de una función. La biblioteca optlib no está vinculada a un tipo de entrada específico para una función optimizada. Además, la biblioteca está construida de tal manera que cuando se usa el algoritmo genético, es posible cambiar fácilmente los algoritmos de cruce, mutación, selección y otras etapas del algoritmo genético. De hecho, el algoritmo genético se ensambla como si fuera de cubos.
El problema de la optimización global.
El problema de optimización generalmente se formula de la siguiente manera.
Para alguna función dada f ( x ), entre todos los valores posibles de x, encuentre un valor x 'tal que f (x') tome un valor mínimo (o máximo). Además, x puede pertenecer a varios conjuntos: números naturales, números reales, números complejos, vectores o matrices.
Por el extremo de la función f ( x ) queremos decir un punto x ' en el que la derivada de la función f ( x ) es igual a cero.
Hay muchos algoritmos que garantizan encontrar el extremo de la función, que es un mínimo o máximo local cerca de un punto de partida dado x 0 . Dichos algoritmos incluyen, por ejemplo, algoritmos de descenso de gradiente. Sin embargo, en la práctica, a menudo es necesario encontrar el mínimo global (o máximo) de una función que, en un rango dado de x, además de un extremo global, tiene muchos extremos locales.
Los algoritmos de gradiente no pueden hacer frente a la optimización de dicha función, porque su solución converge al extremo más cercano cerca del punto de partida. Para problemas de encontrar un máximo o mínimo global, se utilizan los llamados algoritmos de optimización global. Estos algoritmos no garantizan encontrar un extremo global, porque son algoritmos probabilísticos, pero no queda nada más que probar diferentes algoritmos para una tarea específica y ver qué algoritmo enfrentará mejor la optimización, preferiblemente en el menor tiempo posible y con la máxima probabilidad de encontrar un extremo global.
Uno de los algoritmos más famosos (y difíciles de implementar) es el algoritmo genético.
El esquema general del algoritmo genético.
La idea de un algoritmo genético nació gradualmente y se formó a fines de la década de 1960 y principios de la de 1970. Los algoritmos genéticos tuvieron un desarrollo poderoso después del lanzamiento del libro de John Holland "Adaptación en sistemas naturales y artificiales" (1975)
El algoritmo genético se basa en modelar una población de individuos durante un gran número de generaciones. En el proceso del algoritmo genético, aparecen nuevos individuos con los mejores parámetros y mueren los individuos menos exitosos. Para mayor claridad, los siguientes son los términos que se utilizan en el algoritmo genético.
- Un individuo es un valor de x entre el conjunto de valores posibles junto con el valor de la función objetivo para un punto dado x .
- Cromosomas: el valor de x .
- Cromosoma: el valor de x i si x es un vector.
- La función fitness (función fitness, función objetivo) es la función optimizada f ( x ).
- Una población es una colección de individuos.
- Generación: el número de iteraciones del algoritmo genético.
Cada individuo representa un valor de
x entre el conjunto de todas las soluciones posibles. El valor de la función optimizada (en el futuro, por brevedad, suponemos que estamos buscando el mínimo de la función) se calcula para cada valor de
x . Asumimos que cuanto menos importante sea la función objetivo, mejor será esta solución.
Los algoritmos genéticos se utilizan en muchos campos. Por ejemplo, se pueden usar para seleccionar pesos en redes neuronales. Muchos sistemas CAD utilizan un algoritmo genético para optimizar los parámetros del dispositivo para cumplir con los requisitos específicos. Además, los algoritmos de optimización global se pueden utilizar para seleccionar la ubicación de los conductores y elementos en el tablero.
El diagrama estructural del algoritmo genético se muestra en la siguiente figura:
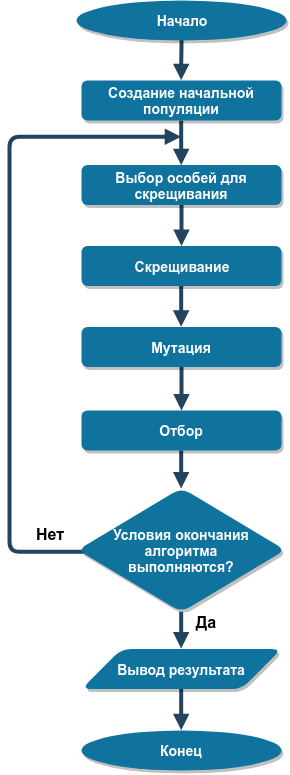
Consideramos cada etapa del algoritmo con más detalle.
Crear una población inicial
La primera etapa del algoritmo es la creación de la población inicial, es decir, la creación de muchos individuos con diferentes valores de los cromosomas x . Como regla general, la población inicial se crea a partir de individuos con un valor de cromosoma aleatorio, mientras se intenta asegurar que los valores de cromosomas en la población cubran el área de búsqueda de solución completa de manera relativamente uniforme, a menos que haya suposiciones sobre dónde puede estar el extremo global.
En lugar de distribuir aleatoriamente los cromosomas, puede crear cromosomas para que los valores iniciales de x se distribuyan uniformemente en toda el área de búsqueda con un paso dado, que depende de cuántos individuos se crearán en esta etapa del algoritmo.
Cuantos más individuos se crearán en esta etapa, mayor será la probabilidad de que el algoritmo encuentre la solución correcta y, a medida que aumenta el tamaño de la población inicial, por regla general, se requieren menos iteraciones del algoritmo genético (número de generaciones). Sin embargo, con un aumento en el tamaño de la población, se requiere un número creciente de cálculos de la función objetivo y el desempeño de otras operaciones genéticas en las etapas posteriores del algoritmo. Es decir, con un aumento en el tamaño de la población, aumenta el tiempo de cálculo de una generación.
En principio, el tamaño de la población no tiene que permanecer constante durante todo el trabajo del algoritmo genético, a menudo a medida que aumenta el número de generación, el tamaño de la población puede reducirse, porque Con el tiempo, un número creciente de personas se ubicará más cerca de la solución deseada. Sin embargo, a menudo el tamaño de la población se mantiene aproximadamente constante.
Selección de individuos para cruces
Después de crear una población, es necesario determinar qué individuos participarán en la operación de cruzamiento (ver el siguiente párrafo). Hay varios algoritmos para esta etapa. La más simple de ellas es cruzar a cada individuo con cada una, pero luego, en el siguiente paso, tendrá que realizar demasiadas operaciones de cruzamiento y calcular los valores de la función objetivo.
Es mejor dar una mayor oportunidad de aparearse con individuos con cromosomas más exitosos (con un valor mínimo de la función objetivo), y aquellos individuos cuya función objetivo es más (peor) para privar a la capacidad de dejar descendencia.
Por lo tanto, en esta etapa, debe crear pares de individuos (o no necesariamente pares si más individuos pueden participar en el cruce), para lo cual la operación de cruce se llevará a cabo en la siguiente etapa.
Aquí también puede aplicar varios algoritmos. Por ejemplo, cree pares al azar. O puede ordenar los individuos en orden ascendente por el valor de la función objetivo y crear pares de individuos ubicados más cerca del comienzo de la lista ordenada (por ejemplo, de individuos en la primera mitad de la lista, en el primer tercio de la lista, etc.) Este método es malo porque lleva tiempo Clasificación de individuos.
El método del torneo es de uso frecuente. Cuando se seleccionan al azar varios individuos para el papel de cada solicitante de cruce, entre los cuales el individuo con el mejor valor de la función objetivo se envía al futuro par. E incluso aquí se puede introducir un elemento de aleatoriedad, dando una pequeña oportunidad para que el individuo con el peor valor de la función objetivo "derrote" al individuo con el mejor valor de la función objetivo. Esto le permite mantener una población más heterogénea, protegiéndola de la degeneración, es decir. de una situación en la que todos los individuos tienen valores cromosómicos aproximadamente iguales, lo que equivale a demorar el algoritmo en un extremo, posiblemente no global.
El resultado de esta operación será una lista de socios para cruzar.
Cruzamiento
El cruzamiento es una operación genética que crea nuevos individuos con nuevos valores cromosómicos. Se crean nuevos cromosomas basados en los cromosomas de los padres. Muy a menudo, en el proceso de cruzar un conjunto de parejas, se crea una hija, pero en teoría, se pueden crear más hijos.
El algoritmo de cruce también se puede implementar de varias maneras. Si el tipo de cromosoma es un número en individuos, lo más simple que se puede hacer es crear un nuevo cromosoma como la media aritmética o la media geométrica de los cromosomas de los padres. Para muchas tareas esto es suficiente, pero la mayoría de las veces se utilizan otros algoritmos basados en operaciones de bits.
Los cruces a nivel de bits funcionan de tal manera que el cromosoma hijo consta de una parte de los bits de uno de los padres y parte de los bits de otro padre, como se muestra en la siguiente figura:
El punto de división principal generalmente se selecciona al azar. No es necesario crear dos niños con esa cruz, a menudo limitada a uno de ellos.
Si el punto de división de los cromosomas originales es uno, entonces ese cruce se llama punto único. Pero también puede usar la división multipunto, cuando los cromosomas originales se dividen en varias secciones, como se muestra en la siguiente figura:
En este caso, son posibles más combinaciones de cromosomas hijos.
Si los cromosomas son números de coma flotante, entonces se les pueden aplicar todos los métodos descritos anteriormente, pero no serán muy efectivos. Por ejemplo, si los números de coma flotante se cruzan en forma de bits, como se describió anteriormente, muchas operaciones de cruce crearán cromosomas hijos que diferirán de uno de los padres solo en el lugar decimal lejano. La situación se agrava especialmente cuando se usan números de punto flotante de doble precisión.
Para resolver este problema, es necesario recordar que los números de coma flotante de acuerdo con el estándar IEEE 754 se almacenan como tres números enteros: S (un bit), M y N, a partir de los cuales el número de coma flotante se calcula como x = (-1) S × M × 2 N. Una forma de cruzar números de punto flotante es dividir primero el número en componentes S, M, N, que son enteros, y luego aplicar las operaciones de cruce de bits descritas anteriormente a los números M y N, seleccionar el signo S de uno de padres, y de los valores obtenidos para hacer un cromosoma hija.
En muchos problemas, un individuo no tiene uno, sino varios cromosomas, e incluso puede ser de diferentes tipos (enteros y números de coma flotante). Entonces hay aún más opciones para cruzar tales cromosomas. Por ejemplo, al crear una hija individual, puede cruzar todos los cromosomas de los padres, o puede transferir completamente algunos cromosomas de uno de los padres sin cambios.
Mutación
La mutación es una etapa importante del algoritmo genético que respalda la diversidad de los cromosomas individuales y, por lo tanto, reduce las posibilidades de que la solución converja rápidamente a un mínimo local en lugar de uno global. Una mutación es un cambio aleatorio en el cromosoma de un individuo que acaba de ser creado por cruce.
Como regla general, la probabilidad de una mutación no se establece muy alta, por lo que la mutación no interfiere con la convergencia del algoritmo, de lo contrario, echará a perder a las personas con cromosomas exitosos.
Además del cruce, se pueden usar diferentes algoritmos para la mutación. Por ejemplo, puede reemplazar un cromosoma o varios cromosomas con un valor aleatorio. Pero la mutación bit a bit se usa con mayor frecuencia cuando uno o varios bits se invierten en el cromosoma (o en varios cromosomas), como se muestra en las siguientes figuras.
Mutación de un bit:
Mutación de varios bits:
El número de bits para una mutación puede estar predefinido o ser una variable aleatoria.
Como resultado de las mutaciones, los individuos pueden ser más exitosos y menos exitosos, pero esta operación permite un cromosoma exitoso con conjuntos de ceros y otros que los individuos parentales no tenían que aparecer con una probabilidad distinta de cero.
Selección
Como resultado del cruce y la posterior mutación, aparecen nuevos individuos. Si no hubiera una etapa de selección, el número de individuos crecería exponencialmente, lo que requeriría más y más RAM y tiempo de procesamiento para cada nueva generación de la población. Por lo tanto, después de la aparición de nuevos individuos, es necesario eliminar a la población de los individuos menos exitosos. Esto es lo que sucede en la etapa de selección.
Los algoritmos de selección también pueden ser diferentes. A menudo, los individuos cuyos cromosomas no se encuentran dentro de un intervalo dado de una búsqueda de solución se descartan primero.
A continuación, puede dejar caer a la mayor cantidad posible de personas menos exitosas para mantener un tamaño de población constante. También se pueden aplicar varios criterios probabilísticos para la selección, por ejemplo, la probabilidad de selección de un individuo puede depender del valor de la función objetivo.
Condiciones finales de algoritmo
Como en otras etapas del algoritmo genético, existen varios criterios para finalizar el algoritmo.
El criterio más simple para terminar un algoritmo es abortar el algoritmo después de un número de iteración (generación) dado. Pero este criterio debe usarse con cuidado, porque el algoritmo genético es probabilístico, y diferentes inicios del algoritmo pueden converger a diferentes velocidades. Por lo general, el criterio de terminación por el número de iteración se usa como un criterio adicional en caso de que el algoritmo no encuentre una solución durante un gran número de iteraciones. Por lo tanto, se debe establecer un número suficientemente grande como el umbral del número de iteración.
Otro criterio de detención es que el algoritmo se interrumpe si no aparece una nueva mejor solución para un número determinado de iteraciones. Esto significa que el algoritmo ha encontrado un extremo global o está atascado en un extremo local.
También hay una situación desfavorable cuando los cromosomas de todos los individuos tienen el mismo significado. Esta es la llamada población degenerada. Lo más probable es que en este caso, el algoritmo esté atascado en un extremo, y no necesariamente global. Solo una mutación exitosa puede sacar a una población de este estado, pero dado que la probabilidad de una mutación generalmente se establece pequeña, y está lejos del hecho de que la mutación creará un individuo más exitoso, la situación con una población degenerada generalmente se considera una excusa para detener el algoritmo genético. Para verificar este criterio, es necesario comparar los cromosomas de todos los individuos, si hay diferencias entre ellos y si no hay diferencias, entonces detenga el algoritmo.
En algunos problemas, no es necesario encontrar un mínimo global, sino más bien encontrar una buena solución, una solución para la cual el valor de la función objetivo sea menor que un valor dado. En este caso, el algoritmo puede detenerse antes de tiempo si la solución que se encuentra en la próxima iteración satisface este criterio.
optlib
Optlib es una biblioteca para el lenguaje Rust, diseñada para optimizar funciones. Al momento de escribir estas líneas, solo el algoritmo genético se implementa en la biblioteca, pero en el futuro se planea expandir esta biblioteca agregando nuevos algoritmos de optimización. Optlib está completamente escrito en Rust.
Optlib es una biblioteca de código abierto distribuida bajo la licencia MIT.
optlib :: genético
A partir de la descripción del algoritmo genético, se puede ver que muchas etapas del algoritmo se pueden implementar de diferentes maneras, seleccionándolas para que para una función objetivo determinada el algoritmo converja a la solución correcta en un tiempo mínimo.
El módulo genético optlib :: está diseñado de tal manera que es posible ensamblar el algoritmo genético "a partir de cubos". Al crear una instancia de la estructura dentro de la cual se llevará a cabo el trabajo del algoritmo genético, debe especificar qué algoritmos se utilizarán para crear la población, seleccionar parejas, cruces, mutar, seleccionar y qué criterio se utiliza para interrumpir el algoritmo.
La biblioteca ya tiene los algoritmos más utilizados para las etapas del algoritmo genético, pero puede crear sus propios tipos que implementen los algoritmos correspondientes.
En la biblioteca, el caso donde los cromosomas son un vector de números fraccionarios, es decir cuando la función f ( x ) se minimiza, donde x es el vector de los números de coma flotante ( f32 o f64 ).
Ejemplo de optimización usando optlib :: genética
Antes de comenzar a describir el módulo genético en detalle, considere un ejemplo de su uso para minimizar la función de Schwefel. Esta función multidimensional se calcula de la siguiente manera:
La función mínima de Schweffel en el intervalo -500 <= x i <= 500 se encuentra en el punto x ' , donde todo x i = 420.9687 para i = 1, 2, ..., N, y el valor de la función en este punto es f ( x' ) = 0.
Si N = 2, la imagen tridimensional de esta función es la siguiente:

Los extremos son más claramente visibles si construimos las líneas de nivel de esta función:

El siguiente ejemplo muestra cómo usar el módulo genético para encontrar la función mínima de Schweffel. Puede encontrar este ejemplo en el código fuente en la carpeta examples / genetic-schwefel.
Este ejemplo se puede ejecutar desde la raíz de origen ejecutando el comando
cargo run --bin genetic-schwefel --release
El resultado debería verse así:
Solution: 420.962615966796875 420.940093994140625 420.995391845703125 420.968505859375000 420.950866699218750 421.003784179687500 421.001281738281250 421.300537109375000 421.001708984375000 421.012603759765625 420.880493164062500 420.925079345703125 420.967559814453125 420.999237060546875 421.011505126953125 Goal: 0.015625000000000 Iterations count: 3000 Time elapsed: 2617 ms
La mayor parte del código de muestra está involucrado en la creación de objetos de rasgos para las diversas etapas del algoritmo genético. Como se escribió al comienzo del artículo, cada etapa del algoritmo genético se puede implementar de varias maneras. Para utilizar el módulo genético optlib ::, debe crear objetos de rasgos que implementen cada paso de una forma u otra. Luego, todos estos objetos se transfieren al constructor de la estructura GeneticOptimizer, dentro del cual se implementa el algoritmo genético.
El método find_min () de la estructura GeneticOptimizer inicia la ejecución del algoritmo genético.
Tipos y objetos básicos
Rasgos básicos del módulo optlib
La biblioteca optlib se desarrolló con el objetivo de agregar nuevos algoritmos de optimización en el futuro, para que el programa pueda cambiar fácilmente de un algoritmo de optimización a otro, por lo tanto, el módulo optlib contiene el rasgo Optimizer , que incluye un método único: find_min (), que ejecuta el algoritmo de optimización en la ejecución. Aquí el tipo T es el tipo del objeto, que es un punto en el espacio de búsqueda de la solución. Por ejemplo, en el ejemplo anterior, este es Vec <Gene> (donde Gene es un alias para f32). Es decir, este es el tipo cuyo objeto se alimenta a la entrada de la función objetivo.
El rasgo Optimizer se declara en el módulo optlib de la siguiente manera:
pub trait Optimizer<T> { fn find_min(&mut self) -> Option<(&T, f64)>; }
El método find_min () del optim_ trait debería devolver un objeto de tipo Opción <(& T, f64)>, donde & T en la tupla devuelta es la solución encontrada, y f64 es el valor de la función objetivo para la solución encontrada. Si el algoritmo no pudo encontrar una solución, entonces la función find_min () debería devolver None.
Dado que muchos algoritmos de optimización estocástica usan los llamados agentes (en términos de un algoritmo genético, un agente es un individuo), el módulo optlib también contiene el rasgo AlgorithmWithAgents con un único método get_agents (), que debería devolver un vector de agente.
Un agente, a su vez, es una estructura que implementa otro rasgo de optlib - Agent .
Los rasgos AlgorithmWithAgents y Agent se declaran en el módulo optlib de la siguiente manera:
pub trait AlgorithmWithAgents<T> { type Agent: Agent<T>; fn get_agents(&self) -> Vec<&Self::Agent>; } pub trait Agent<T> { fn get_parameter(&self) -> &T; fn get_goal(&self) -> f64; }
Para AlgorithmWithAgents y Agent, el tipo T tiene el mismo significado que para Optimizer, es decir, es el tipo de objeto para el que se calcula el valor de la función objetivo.
Estructura del optimizador genético: implementación del algoritmo genético
Ambos tipos se implementan para la estructura GeneticOptimizer : Optimizer y AlgorithmWithAgents.
Cada etapa del algoritmo genético está representada por su propio tipo, que puede implementarse desde cero o usar una de las implementaciones genéticas optlib :: disponibles en su interior. Para cada etapa del algoritmo genético, dentro del módulo genético optlib :: hay un submódulo con estructuras y funciones auxiliares que implementan los algoritmos más utilizados de las etapas del algoritmo genético. Sobre estos módulos se discutirá a continuación. También dentro de algunos de estos submódulos hay un submódulo vec_float que implementa los pasos del algoritmo para el caso en que la función objetivo se calcula a partir de un vector de números de punto flotante (f32 o f64).
El constructor de la estructura GeneticOptimizer se declara de la siguiente manera:
impl<T: Clone> GeneticOptimizer<T> { pub fn new( goal: Box<dyn Goal<T>>, stop_checker: Box<dyn StopChecker<T>>, creator: Box<dyn Creator<T>>, pairing: Box<dyn Pairing<T>>, cross: Box<dyn Cross<T>>, mutation: Box<dyn Mutation<T>>, selections: Vec<Box<dyn Selection<T>>>, pre_births: Vec<Box<dyn PreBirth<T>>>, loggers: Vec<Box<dyn Logger<T>>>, ) -> GeneticOptimizer<T> { ... } ... }
El constructor de GeneticOptimizer acepta muchos tipos de objetos que afectan cada etapa del algoritmo genético, así como la salida de los resultados:
- objetivo: Cuadro <dyn Objetivo <T>> - función objetivo;
- stop_checker: Box <dyn StopChecker <T>> - criterio de detención;
- creador: Box <dyn Creator <T>> - crea la población inicial;
- emparejamiento: Box <dyn Pairing <T>> - algoritmo para seleccionar socios para el cruce;
- cross: Box <dyn Cross <T>> - algoritmo de cruce;
- mutación: Box <dyn Mutation <T>> - algoritmo de mutación;
- selecciones: Vec <Box <dyn Selection <T> >> - un vector de algoritmos de selección;
- pre_births: Vec <Box <dyn PreBirth <T> >> - un vector de algoritmos para destruir los cromosomas fallidos antes de crear individuos;
- registradores: Vec <Box <dyn Logger <T> >> - un vector de objetos que preservan el registro del algoritmo genético.
Para ejecutar el algoritmo, debe ejecutar el método find_min () del rasgo Optimizer. Además, la estructura GeneticOptimizer tiene el método next_iterations (), que puede usarse para continuar el cálculo una vez que se completa el método find_min ().
A veces, después de detener un algoritmo, es útil cambiar los parámetros del algoritmo o los métodos utilizados. Esto se puede hacer usando los siguientes métodos de la estructura GeneticOptimizer: replace_pairing (), replace_cross (), replace_mutation (), replace_pre_birth (), replace_selection (), replace_stop_checker (). Estos métodos le permiten reemplazar los objetos de rasgos pasados a la estructura GeneticOptimizer cuando se crea.
Los tipos principales para el algoritmo genético se analizan en las siguientes secciones.
Rasgo del objetivo - función objetivo
El rasgo del objetivo se declara en el módulo genético optlib :: de la siguiente manera:
pub trait Goal<T> { fn get(&self, chromosomes: &T) -> f64; }
El método get () debería devolver el valor de la función objetivo para el cromosoma dado.
Dentro del módulo optlib :: genetic :: goal , hay una estructura GoalFromFunction que implementa el rasgo Goal. Para esta estructura, hay un constructor que toma una función, que es la función objetivo. Es decir, utilizando esta estructura, puede crear un objeto de tipo Objetivo a partir de una función regular.
Rasgo del creador: crear una población inicial
El rasgo Creador describe el "creador" de la población inicial. Este rasgo se declara de la siguiente manera:
pub trait Creator<T: Clone> { fn create(&mut self) -> Vec<T>; }
El método create () debería devolver el vector de cromosomas en función del cual se creará la población inicial.
Para el caso en el que se optimiza una función de varios números de coma flotante, el módulo optlib :: genetic :: creator :: vec_float tiene una estructura RandomCreator <G> para crear una distribución inicial de cromosomas de forma aleatoria.
En lo sucesivo, el tipo <G> es el tipo de un cromosoma en el vector cromosómico (a veces se usa el término "gen" en lugar del término "cromosoma"). Básicamente, el tipo <G> significará el tipo f32 o f64 si los cromosomas son del tipo Vec <f32> o Vec <f64>.
La estructura de RandomCreator <G> se declara de la siguiente manera:
pub struct RandomCreator<G: Clone + NumCast + PartialOrd> { ... }
Aquí NumCast es un tipo de la caja numérica. Este tipo le permite crear un tipo a partir de otros tipos numéricos utilizando el método from ().
Para crear una estructura RandomCreator <G>, debe usar la función new (), que se declara de la siguiente manera:
pub fn new(population_size: usize, intervals: Vec<(G, G)>) -> RandomCreator<G> { ... }
Aquí el tamaño de la población es el tamaño de la población (el número de conjuntos de cromosomas que se crearán), y los intervalos son el vector de tuplas de dos elementos: el valor mínimo y máximo del cromosoma (gen) correspondiente en el conjunto de cromosomas, y el tamaño de este vector determina cuántos cromosomas hay en el conjunto de cromosomas. cada individuo
En el ejemplo anterior, la función Schweffel se optimizó para 15 variables de tipo f32. Cada variable debe estar en el rango [-500; 500]. Es decir, para crear una población, el vector de intervalo debe contener 15 tuplas (-500.0f32, 500.0f32).
Emparejamiento de tipos: selección de socios para cruzar
El rasgo de emparejamiento se usa para seleccionar individuos que se cruzarán. Este rasgo se declara de la siguiente manera:
pub trait Pairing<T: Clone> { fn get_pairs(&mut self, population: &Population<T>) -> Vec<Vec<usize>>; }
El método get_pairs () toma un puntero a la estructura de Población , que contiene todos los individuos de la población, y también a través de esta estructura puede encontrar los mejores y peores individuos de la población.
El método de emparejamiento get_pairs () debería devolver un vector que contiene vectores que almacenan los índices de individuos que se cruzarán. Dependiendo del algoritmo de cruce (que se discutirá en la siguiente sección), dos o más individuos pueden cruzar.
Por ejemplo, si los individuos con el índice 0 y 10, 5 y 2, 6 y 3 se cruzan, el método get_pairs () debería devolver el vector vec! [Vec! [0, 10], vec! [5, 2], vec! [ 6, 3]].
El módulo de emparejamiento optlib :: genetic :: contiene dos estructuras que implementan varios algoritmos de selección de socios.
Para la estructura RandomPairing , el tipo de emparejamiento se implementa de tal manera que los socios se seleccionan aleatoriamente para el cruce.
Para la estructura del torneo , el rasgo de emparejamiento se implementa de tal manera que se utiliza el método del torneo. El método del torneo implica que cada individuo que participará en la cruz debe derrotar a otro individuo (el valor de la función objetivo del individuo ganador debe ser menor). Si el método del torneo usa una ronda, esto significa que dos individuos son seleccionados al azar, y un individuo con un valor más bajo de la función objetivo entre estos dos individuos ingresa a la futura "familia". Si se utilizan varias rondas, el individuo ganador de esta manera debería ganar contra varios individuos aleatorios.
El constructor de estructura de torneo se declara de la siguiente manera:
pub fn new(partners_count: usize, families_count: usize, rounds_count: usize) -> Tournament { ... }
Aquí:
- partner_count: el número requerido de personas para cruzar;
- Families_count: el número de "familias", es decir conjuntos de individuos que producirán descendencia;
- rounds_count: el número de rondas en el torneo.
Como una modificación adicional del método del torneo, puedes usar el generador de números aleatorios para dar una pequeña oportunidad de derrotar a las personas con el peor valor de la función objetivo, es decir. para hacer que la probabilidad de victoria esté influenciada por el valor de la función objetivo, y cuanto mayor sea la diferencia entre los dos competidores, mayor será la posibilidad de ganar el mejor individuo, y con valores casi iguales de la función objetivo, la probabilidad de victoria de un individuo sería cercana al 50%.
Tipo Cruz - Cruce
Después de que se formaron "familias" de individuos, para cruzar, debe cruzar sus cromosomas para obtener niños con nuevos cromosomas. La etapa de cruce está representada por el tipo Cross , que se declara de la siguiente manera:
pub trait Cross<T: Clone> { fn cross(&mut self, parents: &[&T]) -> Vec<T>; }
El método cross () cruza un conjunto de padres. Este método acepta el parámetro de los padres, una porción de las referencias a los cromosomas de los padres (no a los individuos mismos), y debería devolver un vector de los nuevos cromosomas. El tamaño de los padres depende del algoritmo para seleccionar parejas para cruzar usando el rasgo de Emparejamiento , que se describió en la sección anterior. A menudo se usa un algoritmo que crea nuevos cromosomas basados en los cromosomas de dos padres, luego el tamaño de los padres será igual a dos.
El módulo optlib :: genetic :: cross contiene estructuras para las cuales el tipo Cross se implementa con diferentes algoritmos de cruce.
- VecCrossAllGenes - una estructura diseñada para cruzar cromosomas, cuando cada individuo tiene un conjunto de cromosomas - este es un vector. El constructor VecCrossAllGenes acepta un tipo de objeto Cross que se aplicará a todos los elementos de los vectores cromosómicos principales. En este caso, el tamaño de los vectores cromosómicos progenitores debe ser del mismo tamaño. El ejemplo anterior utiliza la estructura VecCrossAllGenes porque el cromosoma en los individuos utilizados es del tipo Vec <f32>.
- CrossMean es una estructura que cruza dos números de tal manera que, como cromosoma hijo, se calculará un número como el promedio aritmético de los cromosomas originales.
- FloatCrossGeometricMean es una estructura que cruza dos números de tal manera que, como cromosoma hijo, se calculará un número como la media geométrica de los cromosomas originales. Debe haber números de coma flotante como cromosomas.
- CrossBitwise : cruce de dos números en un solo punto bit a bit.
- FloatCrossExp : cruce de un solo punto a nivel bit de números de coma flotante. Independientemente se cruzan mantisa y padres expositores. El niño recibe el signo de uno de los padres.
El
módulo optlib :: genetic :: cross también contiene funciones para números de cruce de diferentes tipos: entero y coma flotante.
Mutación tipo - Mutación
Después de cruzar, es necesario mutar a los niños obtenidos para mantener la diversidad de cromosomas, y la población no se deslizó a un estado degenerado. Para la población, se pretende el rasgo Mutación , que se declara de la siguiente manera:
pub trait Mutation<T: Clone> { fn mutation(&mut self, chromosomes: &T) -> T; }
El único método de mutación () del rasgo Mutación toma una referencia a un cromosoma y debería devolver un cromosoma posiblemente alterado. Como regla general, se establece una pequeña probabilidad de mutación, por ejemplo, un pequeño porcentaje, de modo que los cromosomas obtenidos sobre la base de los padres aún se conservan, y así mejoran la población.
Algunos algoritmos de mutación ya están implementados en el módulo optlib :: genetic :: mutation .
Este módulo, por ejemplo, contiene la estructura VecMutation , que funciona de manera similar a la estructura VecCrossAllGenes , es decir. si el cromosoma es un vector, VecMutation acepta el tipo de objeto Mutación y lo aplica con una probabilidad dada para todos los elementos del vector, creando un nuevo vector con genes mutados (elementos del vector cromosómico).
El módulo optlib :: genetic :: mutation también contiene una estructura BitwiseMutation para la cual se implementa el rasgo Mutation. Esta estructura invierte un número dado de bits aleatorios en el cromosoma que se le transmite. Es aconsejable utilizar esta estructura junto con la estructura VecMutation.
Rasgo prenatal - preselección
Después del cruce y la mutación, generalmente se produce la etapa de selección, en la que se destruyen los individuos que no tienen éxito. Sin embargo, en la implementación del algoritmo genético en la biblioteca optlib :: genética, antes del paso de selección, hay otro paso en el que se pueden descartar los cromosomas fallidos. Este paso se agregó porque el cálculo de la función objetivo para los individuos a menudo lleva mucho tiempo y no es necesario calcularlo si los cromosomas no se encuentran dentro del intervalo de búsqueda conocido. Por ejemplo, en el ejemplo anterior, los cromosomas que no caen en el segmento [-500; 500].
Para realizar dicho prefiltrado, se pretende el rasgo PreBirth , que se declara de la siguiente manera:
pub trait PreBirth<T: Clone> { fn pre_birth(&mut self, population: &Population<T>, new_chromosomes: &mut Vec<T>); }
El único método preBirth () del rasgo PreBirth es una referencia a la estructura de Población mencionada anteriormente, así como una referencia mutable al nuevo vector cromosómico de cromosomas. Este es el vector de cromosomas obtenido después del paso de mutación. La implementación del método pre_birth () debería eliminar esos cromosomas de este vector que obviamente no son adecuados para la condición del problema.
Para el caso en el que se optimiza la función del vector de números de coma flotante, el módulo optlib :: genetic :: pre_birth :: vec_float contiene la estructura CheckChromoInterval , diseñada para eliminar los cromosomas si son un vector de números de coma flotante, y algún elemento del vector no cae en el intervalo especificado.
El constructor de la estructura CheckChromoInterval es el siguiente:
pub fn new(intervals: Vec<(G, G)>) -> CheckChromoInterval<G> { ... }
Aquí, el constructor toma un vector de tuplas con dos elementos: el valor mínimo y máximo para cada elemento en el cromosoma. Por lo tanto, el tamaño del vector de intervalos debe coincidir con el tamaño del vector cromosómico de los individuos. En el ejemplo anterior, se usó un vector de 15 tuplas (-500.0f32, 500.0f32) como intervalos.
Selección Selección - Selección
Después de la selección preliminar de los cromosomas, los individuos se crean y se colocan en la población (Estructura de la población ). En el proceso de creación de individuos para cada uno de ellos, se calcula el valor de la función objetivo. En la etapa de selección, es necesario destruir un cierto número de individuos para que la población no crezca indefinidamente. Para esto, se utiliza el rasgo Selección , que se declara de la siguiente manera:
pub trait Selection<T: Clone> { fn kill(&mut self, population: &mut Population<T>); }
Un objeto que implementa el rasgo de Selección en el método kill () debe llamar al método kill () de la estructura Individual (individual) para cada individuo en la población que necesita ser destruido.
Para omitir a todos los individuos en una población, puede usar un iterador que devuelva el método IterMut () de la estructura de Población.
Como a menudo es necesario aplicar varios criterios de selección, al crear la estructura GeneticOptimizer , el constructor acepta un vector de objetos de tipo Selection.
Al igual que con otras etapas del algoritmo genético, el módulo optlib :: genetic :: selection ya ofrece varias implementaciones de la etapa de selección.
Rasgo StopChecker: criterio de detención
Después de la etapa de selección, debe verificar si es hora de detener el algoritmo genético. Como ya se mencionó anteriormente, en esta etapa, también puede usar varios algoritmos de detención. Para la interrupción del algoritmo, el objeto es responsable de que se implemente el rasgo StopChecker , que se declara de la siguiente manera:
pub trait StopChecker<T: Clone> { fn can_stop(&mut self, population: &Population<T>) -> bool; }
Aquí el método can_stop () debería devolver verdadero si el algoritmo se puede detener, de lo contrario este método debería devolver falso.
El módulo optlib :: genetic :: stopchecker contiene varias estructuras con criterios básicos de detención y dos estructuras para crear combinaciones a partir de otros criterios:
- MaxIterations : criterio de ruptura por número de generación. El algoritmo genético se detendrá después de un número dado de iteraciones (generaciones).
- GoalNotChange : un criterio de interrupción según el cual el algoritmo debería detenerse si no se puede encontrar una nueva solución para un número determinado de iteraciones. O en otras palabras, si durante un número determinado de generaciones no aparecen individuos más exitosos.
- Threshold — , , .
- CompositeAll — , ( - StopChecker). , - , .
- CompositeAny — , ( - StopChecker). , - , .
Logger —
Logger , , , . Logger :
pub trait Logger<T: Clone> {
optlib::genetic::logging , Logger:
- StdoutResultOnlyLogger : después de completar el algoritmo, muestra el resultado del trabajo en la consola;
- VerboseStdoutLogger : al final de cada iteración, se muestra en la consola la mejor solución para esta iteración y el valor de la función objetivo para ella.
- TimeStdoutLogger : al final de la ejecución del algoritmo, se muestra el tiempo que llevó el cálculo a la consola.
El constructor de la estructura GeneticOptimizer como último argumento acepta un vector de rasgos de Logger -objects, que le permite configurar de manera flexible la salida del programa.Funciones para probar algoritmos de optimización
Función Schweffel
. optlib::testfunctions , . optlib::testfunctions .
— , . , :
x' = (420.9687, 420.9687, ...). .
optlib::testfunctions schwefel . N .
, , , , .
:
x' = (1.0, 2.0,… N). .
optlib::testfunctions paraboloid .
Conclusión
optlib , . ( optlib::genetic ), , , , .
optlib::genetic. . , , , , .
, . , ( , ..)
Además, se planea agregar nuevas funciones analíticas (además de la función Schweffel) para probar algoritmos de optimización.
Una vez más, recuerdo los enlaces asociados con la biblioteca optlib:
Espero sus comentarios, adiciones y comentarios.