Hola querido lector! Les presento la traducción al inglés del artículo "Física, la próxima frontera" de Chris Hecker.

Yo, un desarrollador Java novato, me enfrenté al hecho de que los materiales para crear un motor físico en el juego se presentan solo en inglés, por lo tanto, este artículo fue traducido. Habrá tres artículos más en la serie, los publicaré lo antes posible. Que tengas una buena lectura!

Nuevas fronteras en física

No hay duda de que cada año los gráficos del juego son cada vez más realistas. Ya hoy, todos crean (o al menos muestran capturas de pantalla) mundos 3D con mapas de textura, y cuando suficientes personas trabajadoras se unen para trabajar en un proyecto, cada desarrollador puede dibujar miles de millones de polígonos de texturas y sombras realistas por segundo. En términos técnicos, ¿qué queda por hacer para crear un juego de alto nivel? ¿Podrán todos los desarrolladores con una copia del libro "Aprender a usar hardware 3D en 21 días" crear un juego realmente impresionante?

En absoluto Los desarrolladores exclusivos continuarán elevando el listón en muchas tecnologías diferentes (como la complejidad de la GUI, la inteligencia artificial y las redes). Por supuesto, todo esto es muy importante, ni siquiera podemos discutir seriamente ninguno de ellos sin especificar detalles. Sin embargo, hay una tecnología aplicable a todo, que, en mi opinión, se convertirá en un factor decisivo en el futuro cercano: la física.

Considere el siguiente ejemplo: ¿recuerda estos enormes engranajes giratorios en uno de los primeros niveles de Duke Nukem 3D?



Figura 1. Captura de pantalla del juego "Duke Nukem 3D"

Solo imagine que su rotación se describiría no por animación cíclica, sino por un motor físico real. De repente, los engranajes se convierten en algo más que una decoración de juego, justo cuando uno de ellos se desvía del ángulo dado y rueda por el pasillo detrás de ti, como en las películas de Indiana Jones. ¡O imagine que después de disparar un equipo desde un lanzacohetes, rodará por el pasillo y aplastará a su amigo, que se ha arrastrado hacia atrás para matarlo! Los motores físicos hacen que tales situaciones sean reales.

La simulación física es lo que hace que todo el mundo del juego: gracias a él, "aquí" se encuentra aquí, si entiendes lo que quiero decir. Cualquier magia en los gráficos del mundo no permitirá que el jugador se sumerja en el proceso del juego si se interpenetra en otro jugador, o en las paredes del nivel, o si la masa y el momento de la masa no se sienten. Los animadores de Disney descubrieron que este sentimiento de las masas es lo que separa la buena animación de la mala animación. Según el libro épico Disney Animation: The Illusion of Life de Frank Thomas y Ollie Johnston, los animadores de Disney, incluso colgando un póster en el estudio, siempre deben preguntarse: "¿Hay mucho peso, profundidad y equilibrio en su dibujo?" ? "

Pero hoy en día casi todos los juegos tienen un motor de física, ¿verdad? Sin lugar a dudas, esto es lo que evita que su automóvil caiga por el borde del mundo del juego, gracias a esto sus personajes no vuelan al espacio cuando saltan, y esto arroja su bote hacia un lado cuando un cohete explota cerca. Sin embargo, la mayoría de los motores físicos en los juegos modernos son bastante débiles. Solo hacen frente a la tarea de evitar que el automóvil caiga al borde del mundo, pero sus capacidades no son suficientes para llevar el juego a un nuevo nivel, donde los restos de un automóvil destrozado pueden explotar en la pista, causando un vuelco de paredes y otros automóviles.

Otros efectos físicos que a menudo se ignoran incluyen: desde simples efectos de torsión como resultado de un golpe tangente, hasta los personajes del juego que mantienen el equilibrio y se mueven, a diferencia de los estáticamente animados. Creo que muchos desarrolladores ignoran estas posibilidades porque no entienden las matemáticas que describen la física, o estaban demasiado ocupados creando mapas de texturas para aprenderlo. La avalancha de hardware para trabajar con 3D se encargará de esto último, y estoy comenzando una nueva serie de artículos. El primer artículo se encargará de los trámites. Al final de nuestro ciclo, usted mismo puede crear un motor físico que hará que los jugadores se sientan completamente inmersos en el juego, gracias a un realismo increíble o un surrealismo entretenido pero persistente.

Advertencia Física = matemáticas, para completar un proyecto interesante, tendrás que usar ambos. Antes de que esto lo asuste, permítanme señalar que las matemáticas que describen la física no solo son elegantes y hermosas, sino que también tienen un carácter aplicado. Es decir, no es matemática abstracta para las matemáticas. Cada ecuación que usamos tiene un significado físico real. Creamos ecuaciones a partir de un modelo físico y, a cambio, las ecuaciones nos dicen cómo se comporta el modelo a tiempo.

Gran empresa

La física es un amplio campo científico. Pero estamos realmente interesados ​​en su pequeña sección llamada "dinámica", o más precisamente, "dinámica de los sólidos". La dinámica se puede definir en términos de una sección relacionada: cinemática (la doctrina del movimiento en el tiempo). La cinemática no se centra en las causas del movimiento o cómo los cuerpos terminaron donde están, simplemente describe el movimiento. La dinámica, por el contrario, describe las fuerzas y masas que contribuyen a que los valores de la cinemática cambien con el tiempo. Qué tan lejos volará la pelota de béisbol si el tiempo de vuelo es de 10 segundos y su velocidad inicial es de 50 kilómetros / hora, y la trayectoria, una línea recta, es un problema cinemático; qué tan lejos volará la pelota de béisbol en el campo gravitacional de la tierra, si la golpeo con un bate, este es un problema dinámico.

La parte de la dinámica que describe los sólidos se relaciona con las restricciones que agregamos para los objetos simulados. La forma de un cuerpo sólido no cambia durante la simulación: es más probable que el cuerpo sea de madera o metal que como gelatina. Podemos crear figuras articuladas, por ejemplo, de una persona, construyendo cada parte de la figura a partir de un cuerpo sólido y creando ligamentos entre ellas, pero no contaremos con huesos doblados bajo tensión o efectos similares. Esto nos permitirá simplificar nuestras ecuaciones sin perder la calidad del interesante comportamiento dinámico de los cuerpos.

Aunque consideraremos una parte tan pequeña de la dinámica, la dinámica de un cuerpo rígido requerirá una serie de artículos para explicar la esencia. Comenzamos nuestro viaje estudiando los conceptos básicos de la programación de computadoras para describir el movimiento de un cuerpo rígido plano bajo la acción de fuerzas. Repito persistentemente "programación de computadora", porque además de las ecuaciones que escribimos para cinemática y dinámica, también aprenderemos cómo resolver estas ecuaciones usando cálculos con números de coma flotante, lo cual es vital para que cada programador sepa. Digo "completamente sólido" porque solo trataremos el mundo bidimensional a lo largo del próximo artículo y más allá. Los principios, y de hecho más que simples ecuaciones, también pueden transferirse al mundo tridimensional, pero definitivamente todo es mucho más simple en el mundo bidimensional, por lo que estudiaremos allí hasta que tengamos confianza para ingresar al espacio tridimensional. En futuros artículos, aprenderemos a describir el efecto de la rotación, el procesamiento de los contactos de los cuerpos y, por supuesto, cómo hacer todo esto en un mundo tridimensional. Bueno, suficientes palabras! ¡Empecemos!

Trabajar con un derivado

Esto puede ser una sorpresa para usted, pero realmente no puede mover un objeto simplemente empujándolo. Lo sé, piensas que me equivoco al demostrar lo contrario a mí al tirar esta revista a la basura por escribir esas tonterías, ¡pero es verdad! Solo presionar una revista nunca afectará directamente su posición en el espacio. De hecho, la presión ni siquiera afecta directamente su velocidad. Lo que realmente afecta la presión es la aceleración de la revista, y de hecho es una de las conclusiones más importantes en la historia de la ciencia.

Para utilizar este hecho para hacer algo interesante, primero tenemos que hablar sobre la relación de la posición del cuerpo con la velocidad y la aceleración. De hecho, todos estos valores están estrechamente relacionados (como probablemente sepa): la velocidad es un indicador de cambios en las coordenadas del cuerpo a lo largo del tiempo, y la aceleración es un indicador de cambios en la velocidad. La herramienta principal para estudiar los cambios en estas cantidades a lo largo del tiempo es el cálculo diferencial. Si entiendes esto, entonces seguimos adelante. Supongo que eres bueno en matemáticas. Utilizaremos solo cálculos escalares y vectoriales simples (derivados e integrales), pero no será superfluo si está familiarizado con las matemáticas en su conjunto. Como referencia: mi libro favorito sobre computación es Cálculo con geometría analítica de Thomas y Finney.

Las coordenadas, la velocidad y la aceleración son cinemáticas que se discutirán en este artículo. La ubicación de un sólido en un mundo bidimensional es, obviamente, un par de coordenadas X e Y, que denotan las coordenadas del espacio de algún punto dado del cuerpo. La derivada para el vector de coordenadas es el vector de velocidad, y nos muestra en qué dirección se mueve el punto (y el cuerpo, si ignoramos la rotación, lo que está sucediendo ahora) y qué tan rápido se está moviendo. El cálculo vectorial es solo el cálculo escalar de cada elemento del vector, por lo que la derivada de la coordenada X es la velocidad del cuerpo con respecto a X, y así sucesivamente. Introducimos la siguiente notación. Deje que la coordenada del cuerpo sea el vector r, y la velocidad sea el vector v o el vector r con un primo. Obtenemos la ecuación:

$$

$${{dx} \ over {dt}} = v = r '$$

Ecuación 1

Si diferenciamos el vector de velocidad con respecto al tiempo, esto mostrará cómo el vector de coordenadas cambia con el tiempo. La aceleración se determina por analogía. Esta es la primera derivada de la velocidad o la segunda derivada del vector de coordenadas:

$$

$${{d ^ 2 r} \ over {dt ^ 2}} = r '' = {{dr '} \ over {dt}} = {{dv} \ over {dt}} = v' = a$$

Ecuación 2

La integral de la aceleración nos dará velocidad, e integrando la aceleración dos veces, obtenemos la coordenada.

Estas relaciones en cinemática muestran que podemos encontrar la aceleración de un objeto, podemos integrarlo con el tiempo para obtener la velocidad y la coordinación. Como veremos más adelante, recurriremos a la integración muchas veces en nuestro código de simulación y calcularemos una nueva posición para nuestro sólido para cada cuadro. ¡Hurra animación!

Aquí hay un ejemplo simple para un mundo unidimensional que podemos integrar analíticamente. Acordemos que queremos encontrar el cambio de coordenadas desde el final del último cuadro hasta el momento del cuadro actual para dibujar la posición actual. A continuación, decimos que la aceleración de nuestro sólido fue igual a 5 unidades arbitrarias / segundo ^ 2. Usaremos el tiempo transcurrido desde el final del último cuadro como una variable t (en el elemento de integración dt).

$$

$$v (t) = ∫adt = ∫5dt = 5t + C$$

Ecuación 3

Las ecuaciones anteriores muestran que la velocidad es una función del tiempo transcurrido desde el último fotograma. Encontramos la constante de integración, C, que es igual a la velocidad inicial al comienzo del período de integración (en t = 0).

$$

$$v (0) = 5 (0) + C$$

$$

$$v_0 = {C}$$

Ecuación 4

$$

$$v (t) = 5t + v_0 {}$$

Ahora integramos nuestra ecuación de velocidad para encontrar la coordenada (nuevamente, no se olvide de la constante de integración):

$$

$$r (t) = ∫v (t) dt = ∫5t + v_0 dt = {{5} \ over {2}} t ^ 2 + v_0 t + r_0$$

Ecuación 5

Basado en la Ecuación 5, podemos encontrar la posición actual solo por una aceleración dada si conocemos la coordenada inicial y la velocidad (que tomaremos del último cuadro) y el tiempo transcurrido. La variable de entrada es el tiempo, y el valor de la función es la posición actual. También indicaremos el tiempo en la Ecuación 4 para calcular la velocidad final de modo que podamos usar esto como la condición inicial para el siguiente cuadro.

Que la fuerza te acompañe

Ahora nos damos cuenta de que necesitamos establecer la aceleración correctamente para integrar las ecuaciones cinemáticas para obtener la animación. La salida de los altavoces en el escenario. ¿Recuerdas, como dije, presionando algo, que afecta directamente solo la aceleración del cuerpo? Bueno, "ejercer presión" es solo un eufemismo para la frase "aplicar fuerza", una de las dos variables clave en la dinámica, y ahora podemos recurrir a Newton para descubrir cómo las fuerzas afectan la aceleración. La segunda ley de Newton conecta la fuerza F con la derivada de la masa, la segunda magnitud de la dinámica, multiplicada por la velocidad. El producto de masa y velocidad se llama el "impulso del cuerpo", denotado por p:

$$

$$F = p '= {{dp} \ over {dt}} = {{d (mv)} \ over {dt}} = mv' = ma$$

Ecuación 6

La masa es una constante para las velocidades con las que estamos trabajando ahora, esto se deduce de la derivada en la ecuación 6, y obtuvimos la conocida ecuación F = ma (aunque estoy seguro de que Newton inicialmente determinó la fuerza a través de la derivada del momento).

Si solo estuviéramos tratando con puntos materiales, la ecuación 6 es lo que necesitamos en dinámica. Para una fuerza dada de un punto material dado, la aceleración se encuentra dividiendo la fuerza por la masa. Esto nos da aceleración, lo que ayudará a resolver la ecuación de movimiento del ejemplo anterior. Sin embargo, estamos tratando con sólidos con masa distribuida en un área determinada (volumen, cuando se trata del mundo tridimensional), por lo que aún tenemos que trabajar.

Primero, considere un sólido como un conjunto de masas de puntos. Definiremos el momento total, pT, para un sólido, como la suma de los momentos de todos los puntos que componen el cuerpo (uso la indexación superior, porque quiero mostrar más claramente qué valores cuantitativos pertenecen a estos puntos):

$$

$$p ^ T = \ sum_ {i} {m ^ i v ^ i}$$

Ecuación 7

Podemos simplificar enormemente el análisis de la dinámica de un cuerpo rígido introduciendo el concepto del centro de masa (CM). Un vector dirigido al centro de masa es una suma lineal de vectores dirigidos desde todos los puntos de masa de un cuerpo sólido dividido por la masa de todo el cuerpo, M:

$$

$$r ^ {CM} = {\ sum_ {i} {m ^ i r ^ i} \ over {M}}$$

Ecuación 8

Usando la definición del centro de masa, podemos simplificar la Ecuación 7 multiplicando ambos lados de la Ecuación 8 por M, diferenciándolos y luego sustituyendo el resultado en la Ecuación 7:

$$

$${{d (Mr ^ {CM})} \ over {dt}} = {\ sum_ {i} {} {{d (m ^ ir ^ i) \ over dt}}} = {\ sum_ {i} {} {m ^ iv ^ i}} = p ^ T$$

Ecuación 9

El lado derecho de la ecuación 9 es el impulso total como se define en la ecuación 7. Ahora veamos el lado izquierdo de la ecuación: esta es la velocidad en el centro de masa multiplicada por la masa de todo el cuerpo. Mueve el lado derecho hacia la izquierda y obtén:

$$

$$p ^ T = {{d (Mr ^ {CM})} \ over {dt}} = Mv ^ {CM}$$

Ecuación 10

De la ecuación 10 se deduce que el momento lineal es igual a la masa total multiplicada por la velocidad dirigida desde el centro de masa, por lo que no es necesario sumar en la ecuación 7 para encontrar el momento si conocemos la masa del cuerpo y la dirección del vector de velocidad del centro de masa. Además, todos los resultados finales de los cálculos son encontrar las integrales para todo el cuerpo, pero el centro de masa existe y simplifica enormemente la determinación del momento total de la Ecuación 10, por lo que no podemos preocuparnos: para encontrar el momento lineal podemos considerar el cuerpo como un punto material con velocidad y masa dadas.

Por analogía, la fuerza total es una derivada del momento total, por lo que el concepto del centro de masa se puede utilizar para simplificar la ecuación de fuerza:

$$

$$F ^ T = p ^ T = Mv '^ {CM} = Ma ^ {CM}$$

Ecuación 11

En resumen, de la Ecuación 11 se deduce que podemos considerar todas las fuerzas que interactúan con un sólido, como si su vector suma tuviera un efecto en el punto del centro de masa, que contiene la masa de todo el cuerpo. Dividimos la fuerza (lectura de la gravedad) por M para encontrar la aceleración del centro de masa, y luego integramos la aceleración en el tiempo para obtener la velocidad y las coordenadas del cuerpo. Porque ignoramos los efectos de la rotación hasta el próximo artículo; ya tenemos todas las ecuaciones que necesitamos para describir la dinámica de un cuerpo rígido. Tenga en cuenta que la Ecuación 11 no contiene información sobre dónde se dirigen las fuerzas aplicadas al cuerpo. Esto aparecerá cuando tratemos con el momento lineal y el centro de masa, y simplemente aplicamos fuerzas al CM para encontrar la aceleración del centro de masa. Cuando calculemos la rotación del cuerpo bajo la influencia de estas fuerzas en el próximo artículo, veremos cómo se utiliza la coordenada de la aplicación de la fuerza.

Oda a la Alegría

En esta etapa, podemos considerar otro ejemplo de integración analítica, utilizando la Ecuación 11 para encontrar la aceleración del centro de masa en lugar de un valor elegido arbitrariamente = 5. Sin embargo, enfrentamos un problema grave, ya que la integración analítica generalmente no tiene un valor aplicado, porque es demasiado complicado, por lo que nos centraremos en la llamada integración numérica de ecuaciones diferenciales ordinarias (EDO). ¡Vaya, eso suena a matemáticas reales! Una vez que aprenda esto, será hora de subir el listón. Afortunadamente, la integración numérica de las EDO no es tan difícil como podría parecer a primera vista. ¡Para entender lo que esto significa, pasamos de las palabras a los hechos!

Entonces, una ecuación diferencial es una ecuación que contiene derivadas de cantidades dependientes además de la función en sí misma, variables independientes y parámetros. Esto es detallado, pero aquí hay un ejemplo de una fuerza que varía en el tiempo en un mundo unidimensional: F = 2t, F es una cantidad dependiente yt es independiente. El valor de F está determinado solo por F. Deje que la ecuación de fuerza dependa solo de la velocidad de nuestro cuerpo.La fuerza de la resistencia del aire aumenta al aumentar la velocidad de la aeronave. Volvamos al ejemplo en el mundo unidimensional, ¿qué pasa si F = -v significa que la fuerza de fricción ralentiza nuestro cuerpo en proporción a la velocidad? Tenemos un problema, porque resolvemos la ecuación de la siguiente manera: F = ma = -v y, dividiendo por m, obtenemos (recuerde que la aceleración es una derivada de la velocidad):

$$

$$a = {{dv}\over {dt}} = {-v\over m}$$

Ecuación 12

Esta ecuación diferencial (la ecuación de velocidad contiene la derivada de velocidad en la ecuación 12) se llama ecuación diferencial ordinaria, porque contiene solo derivadas ordinarias de cantidades dependientes (en oposición a derivadas parciales, que constituyen ecuaciones diferenciales parciales [PDEs], sobre las cuales no estamos hablaremos)

Ahora pasemos a la siguiente parte de nuestra frase: integración. ¿Cómo integramos previamente dv / dt para encontrar v en las condiciones de esta ecuación?

Esto parecerá increíble, pero casi todas las ecuaciones en física son diferenciales, por lo que las EDO han sido bien estudiadas. Las ecuaciones diferenciales a menudo se pueden encontrar en la física, porque a menudo la tasa de cambio de una cantidad cuantitativa depende de la cantidad misma. Por ejemplo, ya hemos notado que el frenado (la magnitud de un cambio en la velocidad), incluida la velocidad de la resistencia del aire, depende de la velocidad. Otros ejemplos de la física: enfriamiento (la tasa de pérdida de calor depende de la temperatura actual) y descomposición radiactiva (la tasa de descomposición depende de la cantidad de material radiactivo presente).

La última palabra en nuestra frase, numérica, es nuestra salvación. Digo esto porque la teoría de la integración analítica de ecuaciones diferenciales, incluso las más simples, es enorme y bastante confusa. Aunque, irónicamente, la integración de las EDO utilizando métodos numéricos informáticos es en realidad relativamente fácil de entender. A continuación, describiré un integrador numérico simple basado en el método de Euler, y lo refinaré en el próximo artículo.

Casi todos los integradores numéricos, pero ninguno tan explícito como el método de Euler, se basan simplemente en la antigua definición de computación a través de la primera derivada de la inclinación: dy / dx determina la pendiente de y dependiendo de x. Por ejemplo, si tenemos la ecuación lineal y = 5x, dy / dx = 5 significa que la pendiente es una constante igual a 5 para cualquier x, y, como puede suponer, esta es una línea recta. Un ejemplo un poco más difícil es la parábola y = x2. En este caso, dy / dx = 2x, y esta es una función para determinar la nueva inclinación para cada coordenada x. Represente y = x2 en la Figura 2: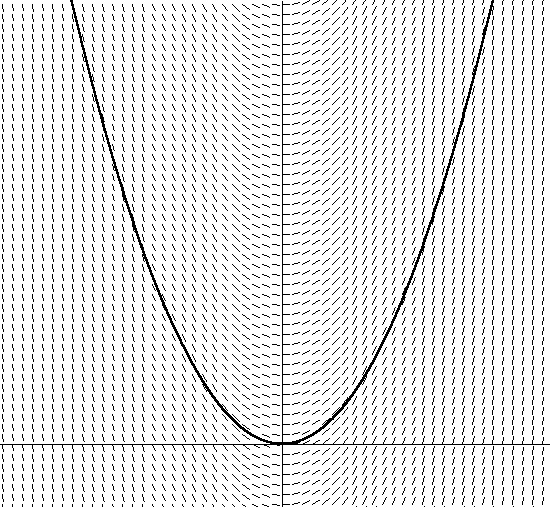



Figura 2. y = x2

Además de esto, también tracé la dirección del vector oblicuo resolviendo la ecuación dy / dx = 2x + C para todas las x. Preste atención al hecho de que el ángulo del vector inclinado es igual a la tangente del ángulo tangente en este punto. Tenga en cuenta también que hay muchas parábolas diferentes que satisfacen el ángulo del conjunto de tangentes, que difieren solo en un desplazamiento a lo largo del eje y. Cada una de estas parábolas se obtiene usando diferentes constantes de integración, que están contenidas en la ecuación dy / dx = 2x + C. La parábola que imaginé tiene una constante de integración de 0. Si elijo otra constante, por ejemplo, 1, obtengo la ecuación y = 2x + 1. Esto significa que hay una parábola similar con un desplazamiento de 1 unidad en el eje y.

Ahora piense en el hecho de que si no conoce el campo de vectores en la Figura 2 definido por una parábola, simplemente siéntese en un charco. Entonces, si desea resolver la ecuación tangente, solo necesita seguir la dirección del vector en cada punto, cambiando la dirección de acuerdo con el cambio en la dirección del campo vectorial. Te sorprenderá que después de un tiempo, verás que te estás moviendo a lo largo de una trayectoria parabólica (o a lo largo de una sección de la parábola), dependiendo de dónde empezaste. Sin darse cuenta, integró la ecuación del campo vectorial. Encontraste una parábola específica (dependiendo de dónde comenzaste o de las condiciones iniciales), usando solo la ecuación derivada (calculando dy / dx a medida que te mueves en el campo vectorial).

Hacer lo mismo para una ecuación diferencial real también es simple. Para una ecuación diferencial del tipo dy / dx = f (x, y), encontrar la derivada dy / dx como una tangente a f (x, y) describe el ángulo de inclinación de la tangente para cada coordenada en el gráfico x, y. Si está trazando un campo vectorial dado por dy / dx = f (x, y), puede seguir esto por analogía con una parábola al encontrar la derivada en cada punto y seguir en esa dirección. La Figura 2 muestra el campo vectorial para la Ecuación 12, nuestra ecuación de resistencia al aire, con velocidad a lo largo del eje vertical y tiempo a lo largo de la horizontal (elegí arbitrariamente m = 1 para este gráfico).



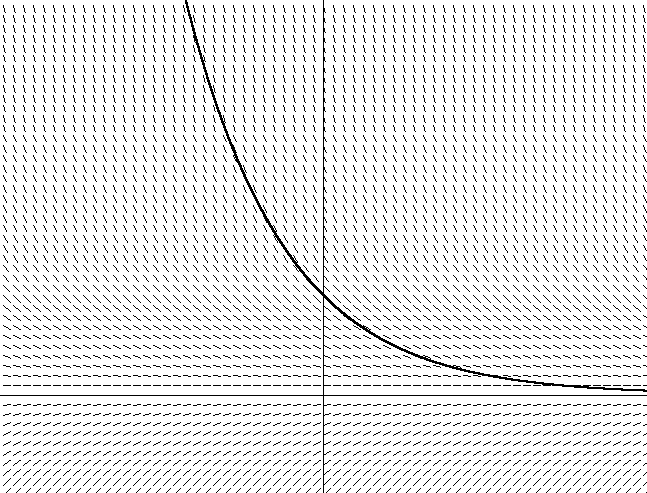Figura 3. dv / dt = -v / m

También muestra una de las muchas curvas posibles. Puede notar que si elige la posición inicial en el gráfico (que depende de la velocidad inicial en la ecuación), con el tiempo, la velocidad tenderá a cero, porque la fuerza de fricción ralentiza el cuerpo. También puede ver cómo la disminución de la velocidad depende del valor actual de la velocidad: cuanto más rápido se mueva, más rápido disminuirá. Esto se hace evidente cuando lo mismo se deduce de la ecuación 12.

La integración numérica es similar a lo que hicimos en el gráfico. El algoritmo de Euler para la integración numérica simplemente sigue el campo vectorial de acuerdo con la posición inicial al encontrar la derivada de la ecuación (-v / m para nuestro ejemplo con la fuerza de fricción) para determinar la pendiente en el punto actual, y luego simplemente avanza paso a paso en el tiempo, dependiendo de valor sin cambios de h, a lo largo de la pendiente. Luego, se calcula una nueva posición para determinar la nueva pendiente después de un cierto intervalo de tiempo:

$$

$$y_{n+1} ≈ y_{ n } + {h(dy_{ n })\over dx}$$

O más precisamente para nuestra ecuación de resistencia al aire:

$$

$$v_{ n+1 } ≈v_{ n }+{h( -v_{n})\over m}$$

Obviamente, el método de Euler produce un pequeño error con cada paso de tiempo, ya que el vector de velocidad real (y, por lo tanto, la curva de solución) se dobla con una desviación en cada punto, y el algoritmo de Euler se desvía ligeramente del ángulo de inclinación. Pero si el paso de tiempo, h son cantidades bastante pequeñas, el error tiende a cero. Discutiremos esto con más detalle en el futuro.

Esto es todo lo que necesita saber sobre la integración numérica utilizando el método Euler. Puede preguntar cómo vamos a integrar la velocidad para obtener la coordenada. Simplemente usamos el método de Euler nuevamente para integrar dr / dt = v, tal como integramos dv / dt = a, por analogía. Obtenemos dos ecuaciones diferenciales conectadas (una más de nuestra victoria):

$$

$$v_{n+1} ≈ v_n+hv'=v_n+{h F_n\over M }$$

$$

$$r_{ n+1 } = r_n + hr_n'= r_n+hv_n$$

Esto nos da un algoritmo alternativo para calcular la coordenada después de la acción de cualquier fuerza aplicada arbitrariamente sobre nuestro objeto (que puede depender de la velocidad, como vimos, o el tiempo, o incluso la posición de nuestro cuerpo y otros cuerpos, ¡o todo a la vez!). Para el método de Euler, no importa cómo se vea la fuerza aplicada, porque puede calcularla en cualquier momento. Euler está interesado en la magnitud del efecto de la fuerza sobre la masa, según lo inclinado, y eso es todo.
Me quedé sin espacio, así que no tengo forma de proporcionar enlaces. La próxima vez aconsejaré varios libros maravillosos y descubriremos cómo calcular la rotación de sólidos.

Y aunque su cuerpo no es tan sólido como nos gustaría, Chris Hecker tiene una personalidad dinámica. Si aplica la fuerza, él contestará el correo electrónico checker@bix.com.

Notas del traductor: aquí se presenta un juego de palabras, se reproduce el tema del artículo y su contenido.

PD: El autor de la traducción expresa un agradecimiento especial a los usuarios de berez y MarazmDed por su edición de la traducción. Gracias