Pegado por docenas de sensores, el "objeto de investigación" durante las pruebas dinámicas a gran escala (por ejemplo, al estudiar la actividad vibratoria del vehículo) nos proporciona fácilmente una gran cantidad de datos, pero a menudo no está muy claro qué hacer con él. Lo mismo ocurre con la simulación de modelos de procesos dinámicos de sistemas con un gran número de grados de libertad.
Esto puede no estar completamente claro para aquellos que no encuentran un problema regularmente, pero mirar la animación correspondiente de un proceso estocástico en el tiempo y el espacio, como regla, es casi inútil. Dónde se rompe o por qué se sacude así, generalmente "no visible". Lo que surgió además de la animación, te lo diré a continuación, pero lo recomendaré.
Por medio de un procedimiento elemental, también se pueden obtener las "formas" espaciales de las oscilaciones mismas, además, son precisamente las manifestaciones reales en condiciones de carga dadas y la intensidad de su manifestación (dispersión; si se desea, los procesos mismos).
Fuente
multicanal
el proceso
 | Descomposición
|
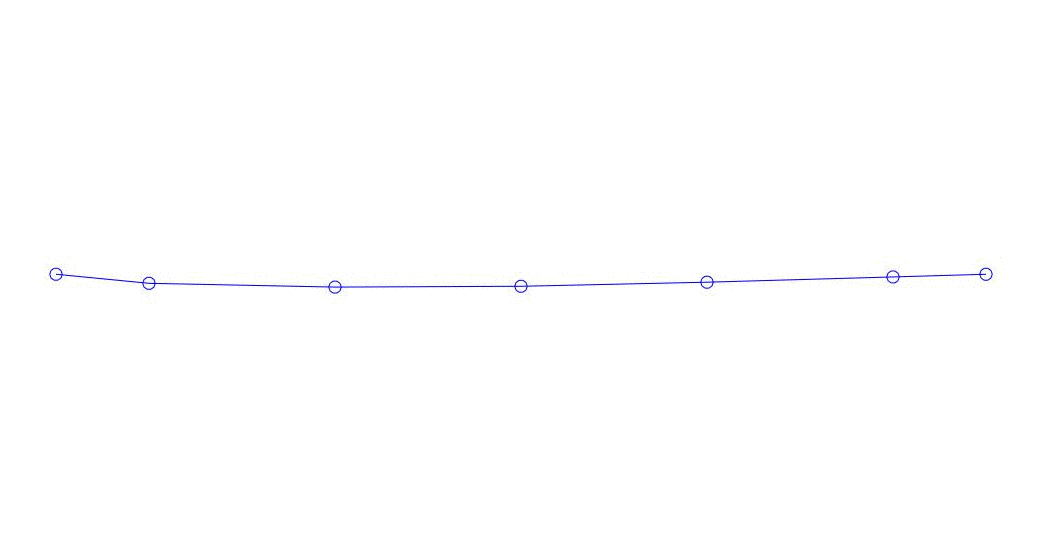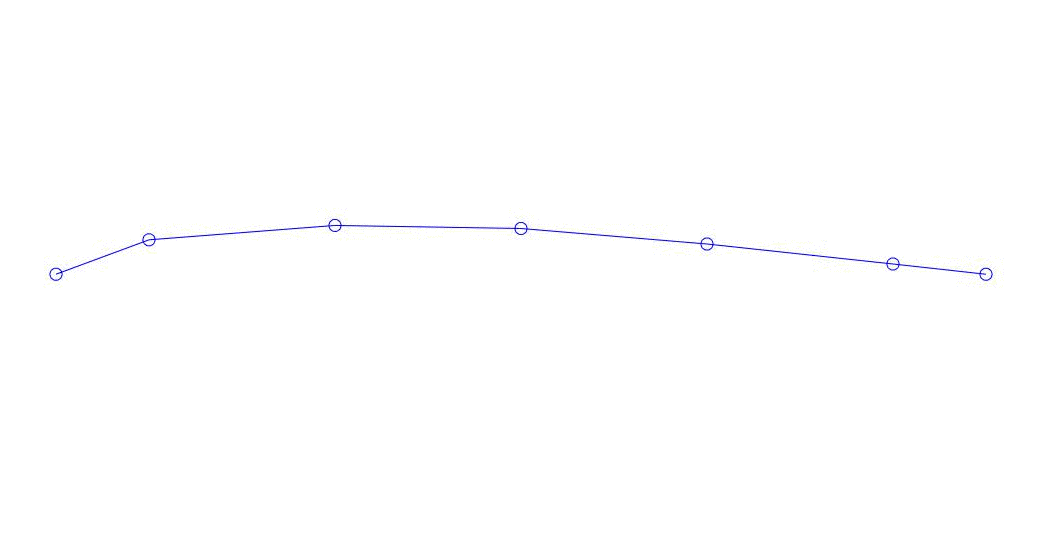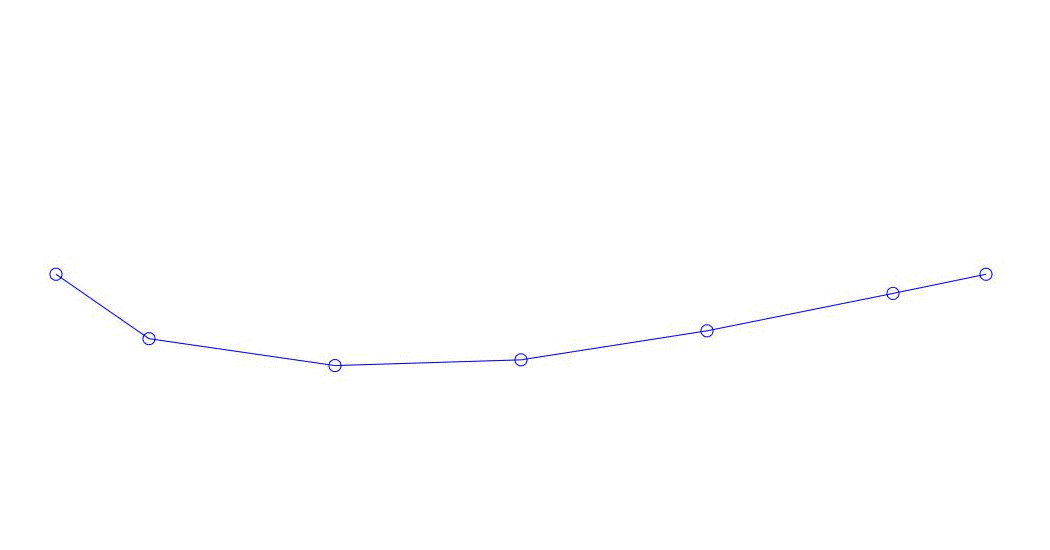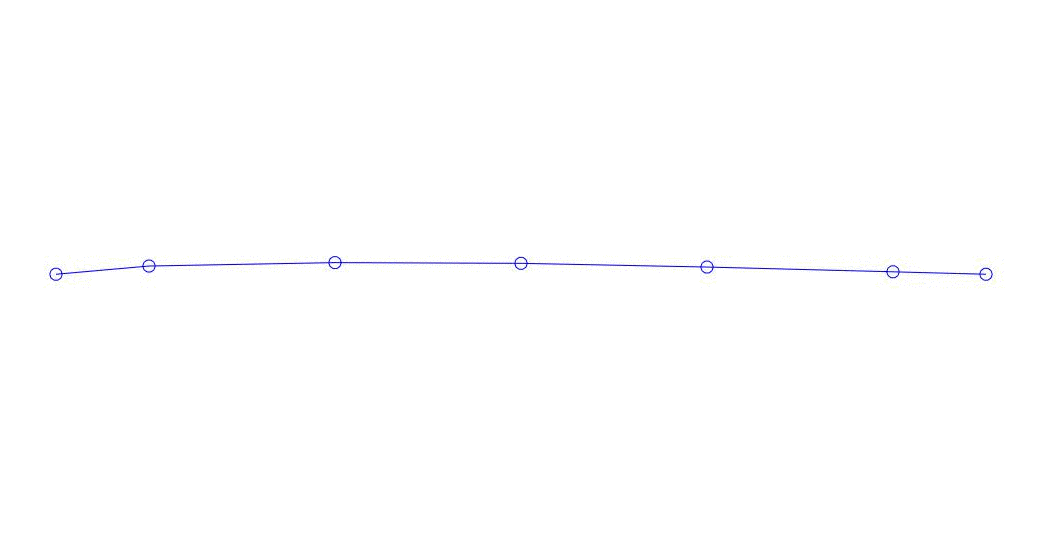
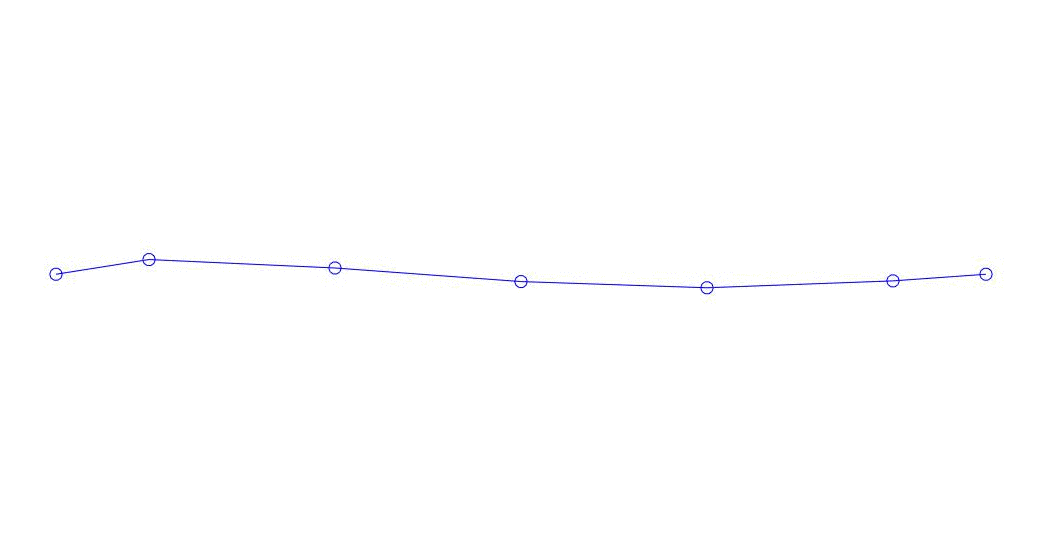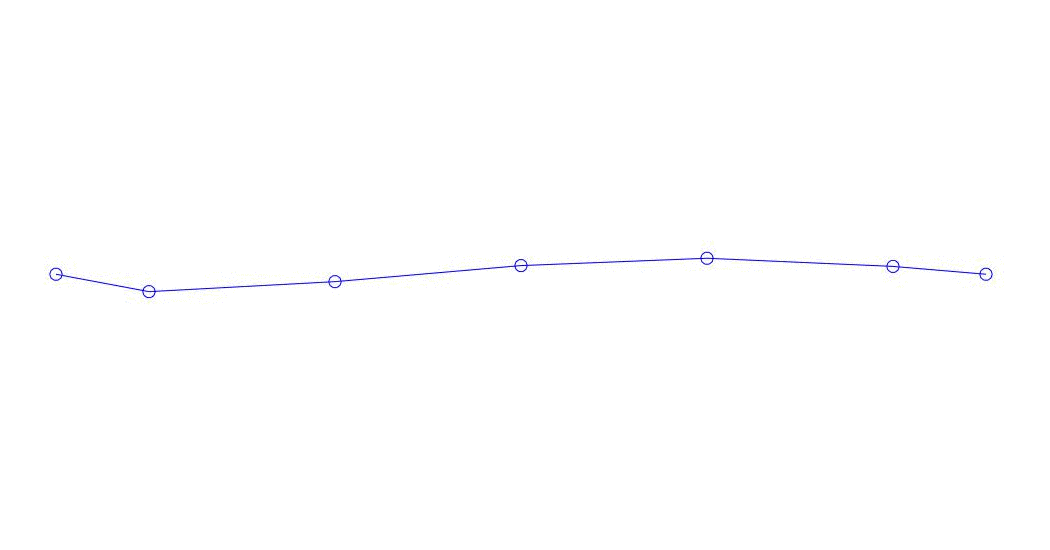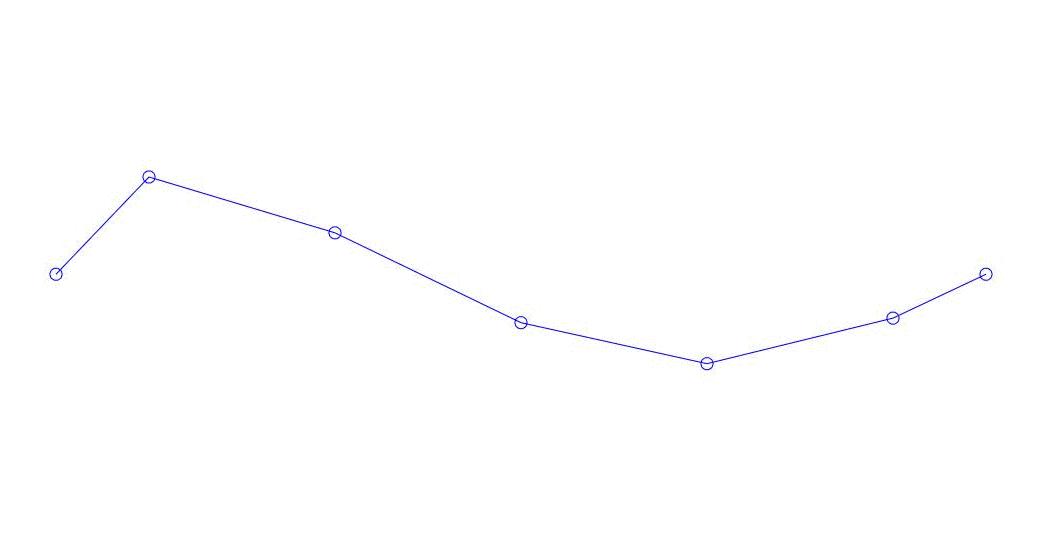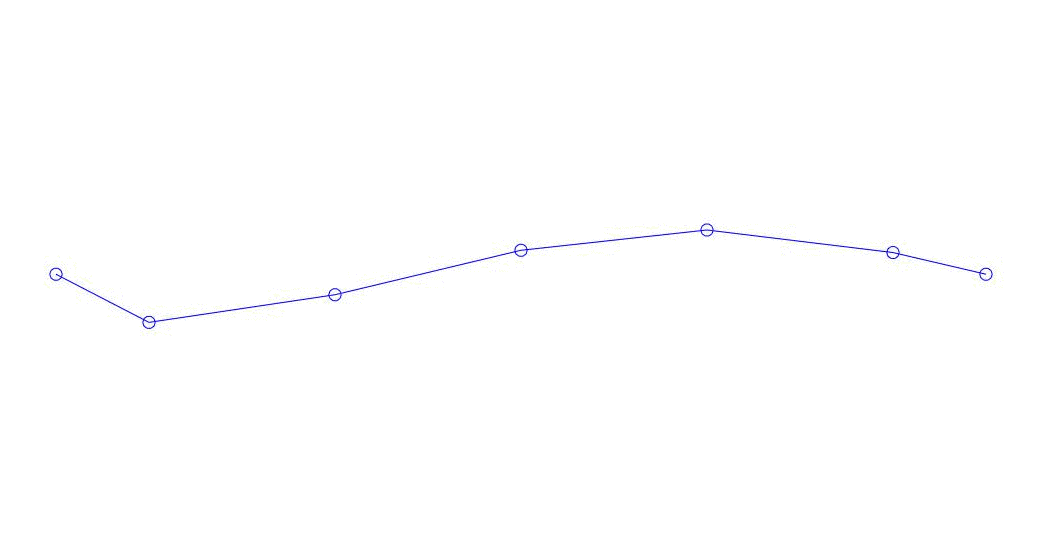
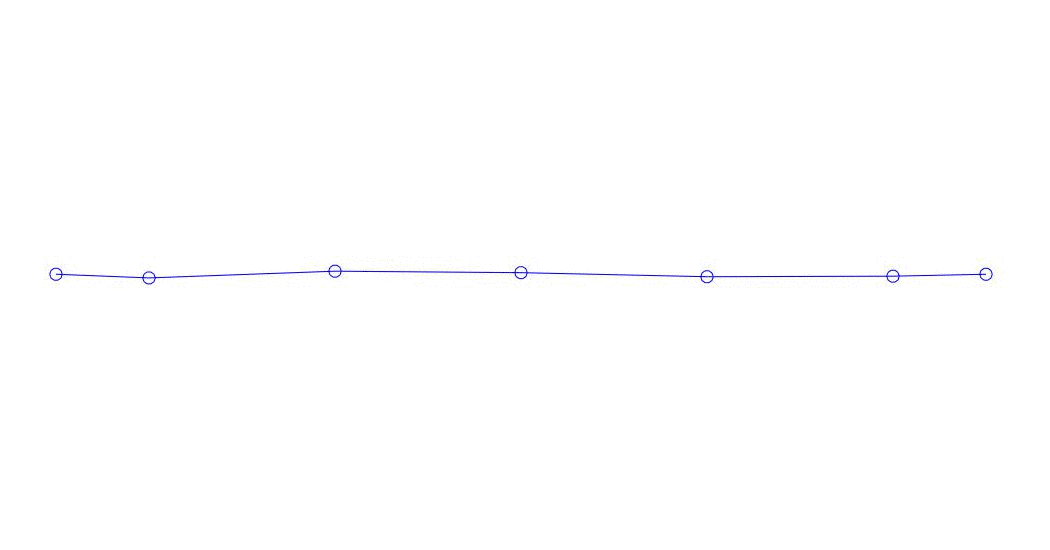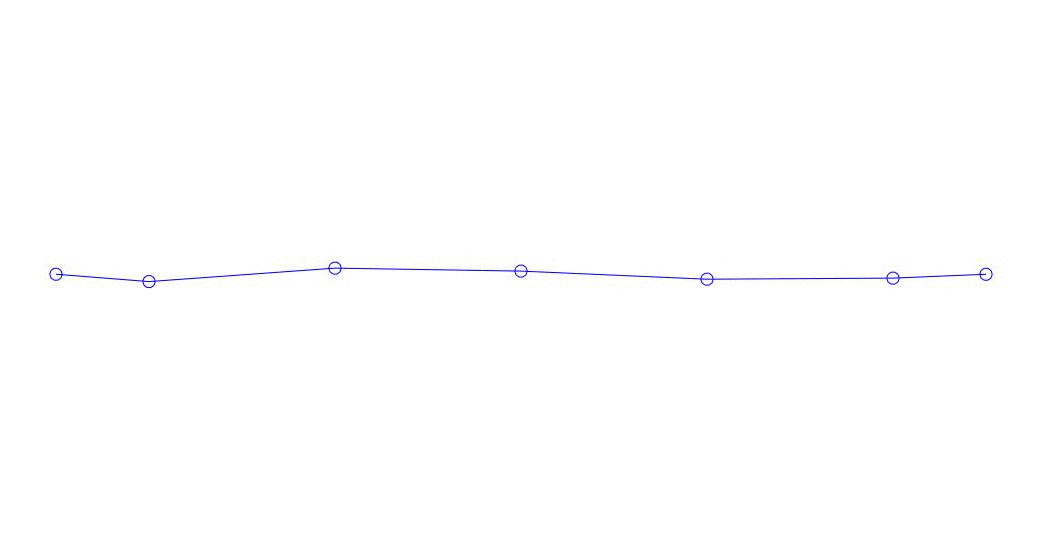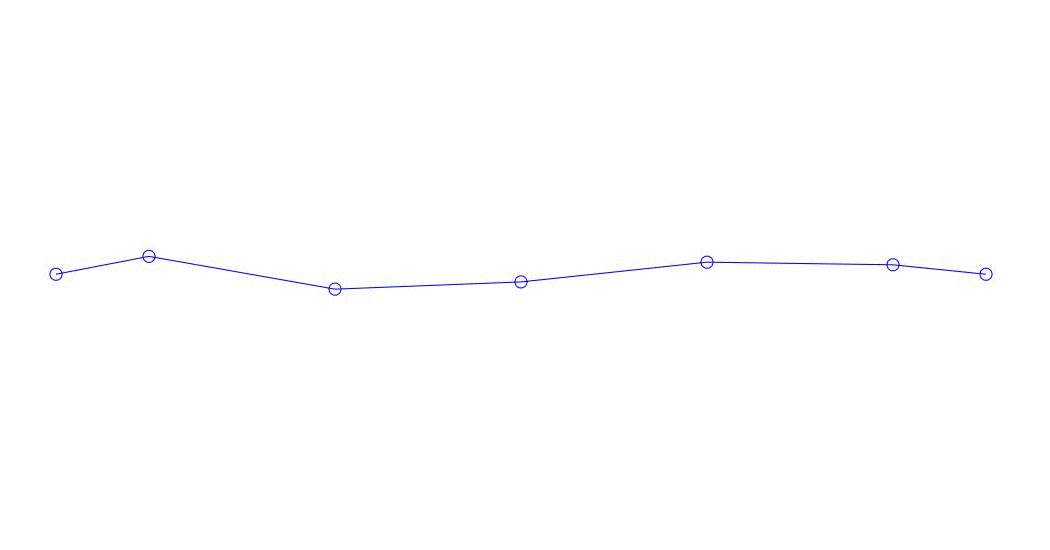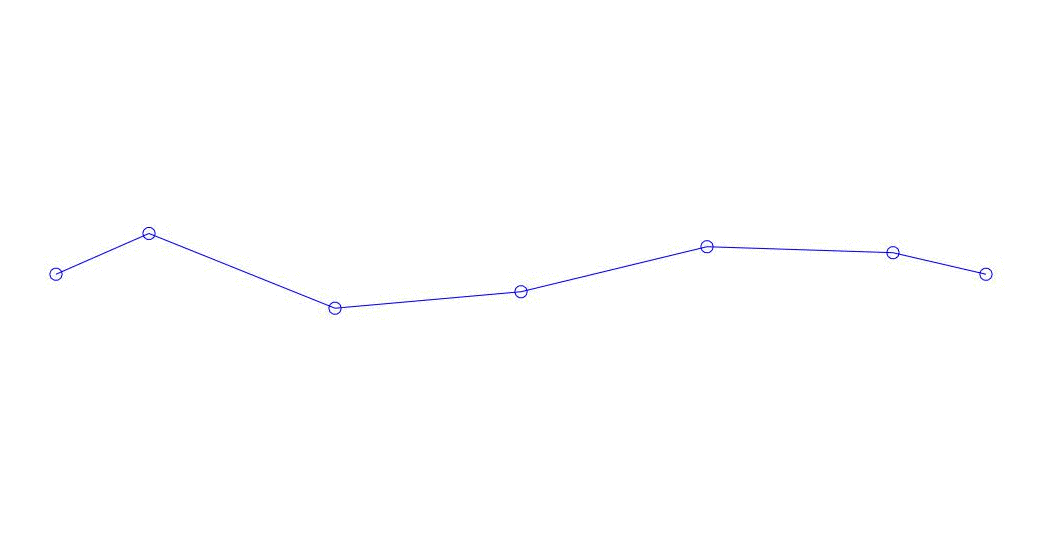
Fig. 1 Expansión de una respuesta multicanal en pseudo-formas. "Cadena en un medio viscoso" (ver figura 2)
Además de la animación, se conocen estudios "por pares" (espectros mutuos, etc.) que, por supuesto, no ofrecen una imagen general.
Tales métodos son bastante obvios: al "cortar" bandas muy estrechas del espectro correspondientes a picos resonantes en los espectrogramas, los métodos de espectrogramas (nuevamente "pares") producen casi formas de vibraciones casi armónicas (altamente correlacionadas).
Además de la obvia complejidad técnica, la desventaja de tales métodos es que generalmente necesita elegir "exitosamente" un canal de "referencia", que no siempre es posible. Como resultado, se producen errores muy grandes en las fases mutuas de los procesos. Además, la forma espacial distinguida de las oscilaciones y sin tales errores, debido a las propiedades de un sistema lineal, puede resultar "compleja" (no fase), lo que su valor para el análisis subjetivo posterior generalmente (no siempre) se reduce significativamente.
Se conoce un estudio de 4 canales de las vibraciones torsionales (el sistema portador de un autobús promedio), que se asigna en un proceso utilizando la forma vibratoria espacial determinada por la inspiración del investigador: se agregaron las lecturas de dos sensores ubicados en diagonal en las esquinas del cuerpo (tomadas de "+"), de fueron restados (tomados de "-") el testimonio de otros dos ubicados axisimetricamente.
Incluso con una pequeña cantidad de sensores, este enfoque puede no ser del todo bueno. Por ejemplo, el bastidor de un camión suele ser mucho más maleable en la parte del sub-motor (delantero), respectivamente, una forma de torsión, tal vez debería asumirse en una forma más compleja (probablemente con algunos coeficientes "crecientes" para los sensores delanteros, y al mismo tiempo, la cuestión de corroborar lo aceptado modelos). Con un mayor número de canales de vigilancia, todo esto es muy complicado y está poco justificado.
La separación explícita (en procesos separados) de varios modos de vibración (modos), previamente determinada a partir de otro experimento o simulación, fue propuesta por mí (probablemente, no solo por mí) y fue llamada por mi jefe y luego "el método de descomposición modal". Se suponía que debía analizar los resultados de las pruebas de campo de tal manera y determinar los vectores de sus propias formas mediante pruebas de banco (o modelado de elementos finitos).
En realidad, hicieron sobre esto, pero al mismo tiempo resultó que.
Está claro que los "experimentadores de banco", en contraste con los "polígonos", están disponibles para la observación sincrónica, un verdadero proceso perturbador. Esto les dio una gran ventaja: podían determinar las verdaderas funciones de transferencia y usar el hardware y el software disponibles para determinar experimentalmente sus propias formas y frecuencias de vibraciones estructurales (basadas en el ajuste de corte, "cortando" los rangos de frecuencia "a ojo" e indicando al sistema cuántas formas hay encontrar; también más bien arte que ciencia, pero aún así).
Sin embargo Claramente evitaron explorar un objeto como un ensamblaje de automóvil, prefiriendo marcos individuales, cuerpos de soporte, etc. - objetos con muy baja amortiguación. Se trata de pruebas de banco modales: la determinación de frecuencias y formas naturales. No se trata de simulación. Los modos intrínsecos de vibración plausibles en objetos ligeramente más fuertemente amortiguados se pueden obtener experimentalmente, pero significativamente más difícil.
La información muy valiosa resultó ser sobre estas "preferencias". Si es muy, muy brevemente, solo las conclusiones que se alcanzaron gradualmente: esforzarse por descomponer la respuesta precisamente en las verdaderas formas adecuadas de la construcción apenas vale la pena, a pesar de la "belleza" de la idea.
Si está "en sus dedos", entonces la razón es probable que tenga una alta probabilidad, tal que, dependiendo de la perturbación externa, los "modos propios de las oscilaciones" (más precisamente, los procesos "modales" estacionarios correspondientes a los modos propios de las oscilaciones) probablemente serán así o de lo contrario, están correlacionados entre sí, formando algunas otras formas espaciales de vibraciones, en un grado u otro diferente de las suyas, y esto naturalmente se manifiesta en una fuerte dependencia de la amortiguación de la estructura.
Como una breve explicación "por el contrario", dos armónicos "no amortiguados" diferentes no están correlacionados, por supuesto, siempre son nada. (Explicación. El efecto antes mencionado de "mezclar formas propias" se observa tanto en ausencia de "no linealidades significativas" como fuera de "formas complejas" con amortiguación "desproporcionada" en sistemas lineales).
Con base en lo anterior, se propone presentar la respuesta del sistema como la suma de varios procesos independientes de correlación, como ciertas formas de vibración (flexión, torsión, etc.). Tal análisis es muy simple, como regla, da resultados muy valiosos. Las formas obtenidas pueden ser similares a los modos propios de oscilación del sistema, o pueden no serlo, pero siempre reflejan el comportamiento del sistema precisamente en condiciones de influencia externa real. además, reflejan lo más simple e informativo posible, y su secuencia, clasificada por sus variaciones, es una serie aproximada.
Para obtener la descomposición que nos interesa, consideramos (1),
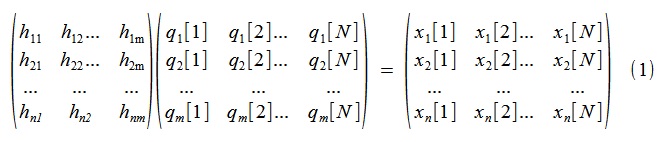
o, lo mismo, de forma compacta, (2),
donde
x es la respuesta física del canal n del sistema con la duración de N muestras obtenidas directamente en el experimento,
q es el proceso "modal" real del canal m con canales mutuamente no correlacionados, H es la matriz de columnas que describe los modos deseados de vibración en fase ("real").
En términos generales, se espera posteriormente m <n (el número de formas es menor que el número de canales de respuesta física), pero inicialmente asumimos que m = n, luego, si H y
q son de rango n, (2) en cualquier caso, se satisface sin un residuo, obviamente llegamos a
| H · Rqq [0] · H T = Rxx [0] (3) |
o con más detalle
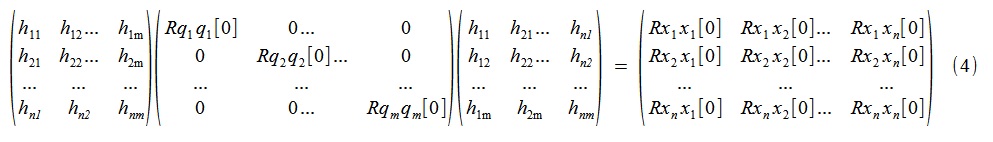
Es decir, la búsqueda de los modos de vibración "pseudo-apropiados" buscados y los procesos correspondientes no correlacionados (con retraso cero)
q se reducen a la descomposición espectral (en términos de vectores y números propios) de la matriz simétrica Rxx [0] (compuesta de los valores de correlaciones automáticas y cruzadas de los procesos
x para lag Δτ = 0) Sus propios vectores ortonormales nos dan las formas deseadas, y los valores propios reales dan las variaciones de los procesos correspondientes (además de los significativos, probablemente habrá variaciones de ~ 0, por lo que en la práctica generalmente m <n). Si lo desea, aún puede construir los procesos en forma de realizaciones temporales, encontrar sus espectros, etc.
Para aclarar lo anterior, consideramos un modelo de un sistema mecánico lineal con cinco grados de libertad, que simula aproximadamente el comportamiento de una cuerda en un medio viscoso (Fig. 2),
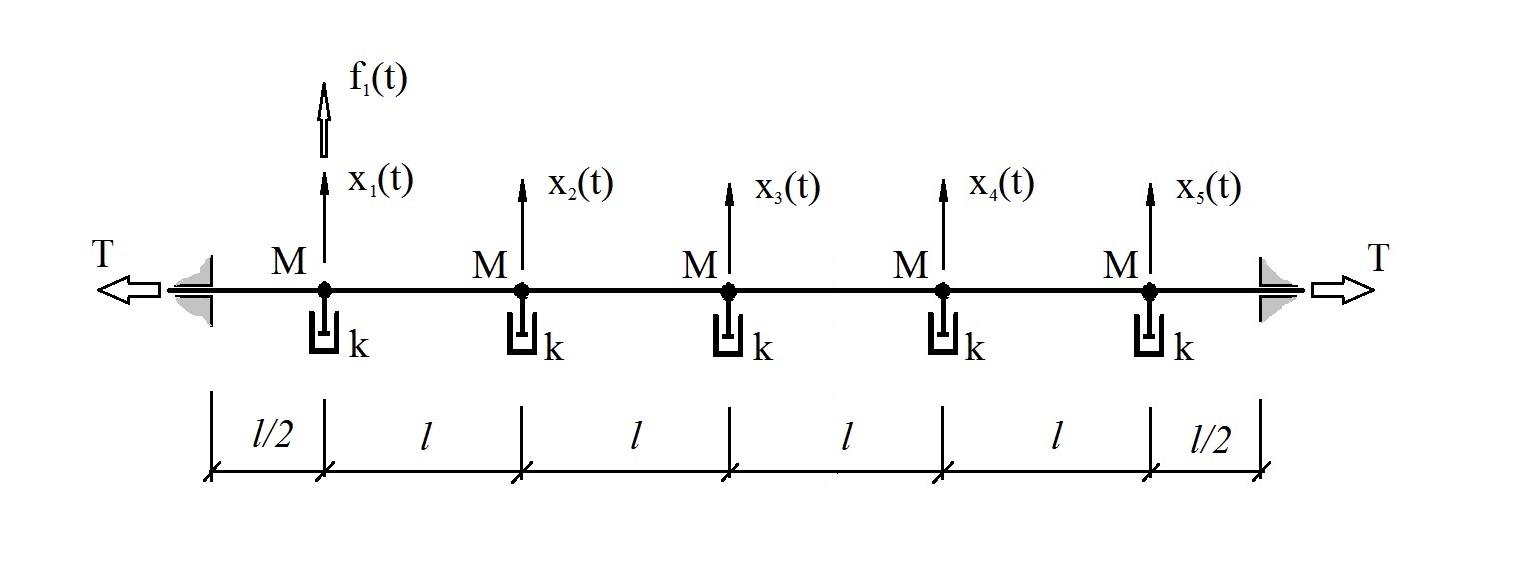Fig. 2 Sistema de prueba.oscilando bajo la influencia de la perturbación estocástica f
1 [i] del tipo de ruido rosa (Fig. 3), intervalo de muestreo Δt = 0.01 s, longitud de implementación 25000 muestras. (En adelante, las estimaciones de PSD se obtienen por el método Welch, longitud del segmento 1024, se aplica la ventana de Hamming 60% de superposición de segmentos).
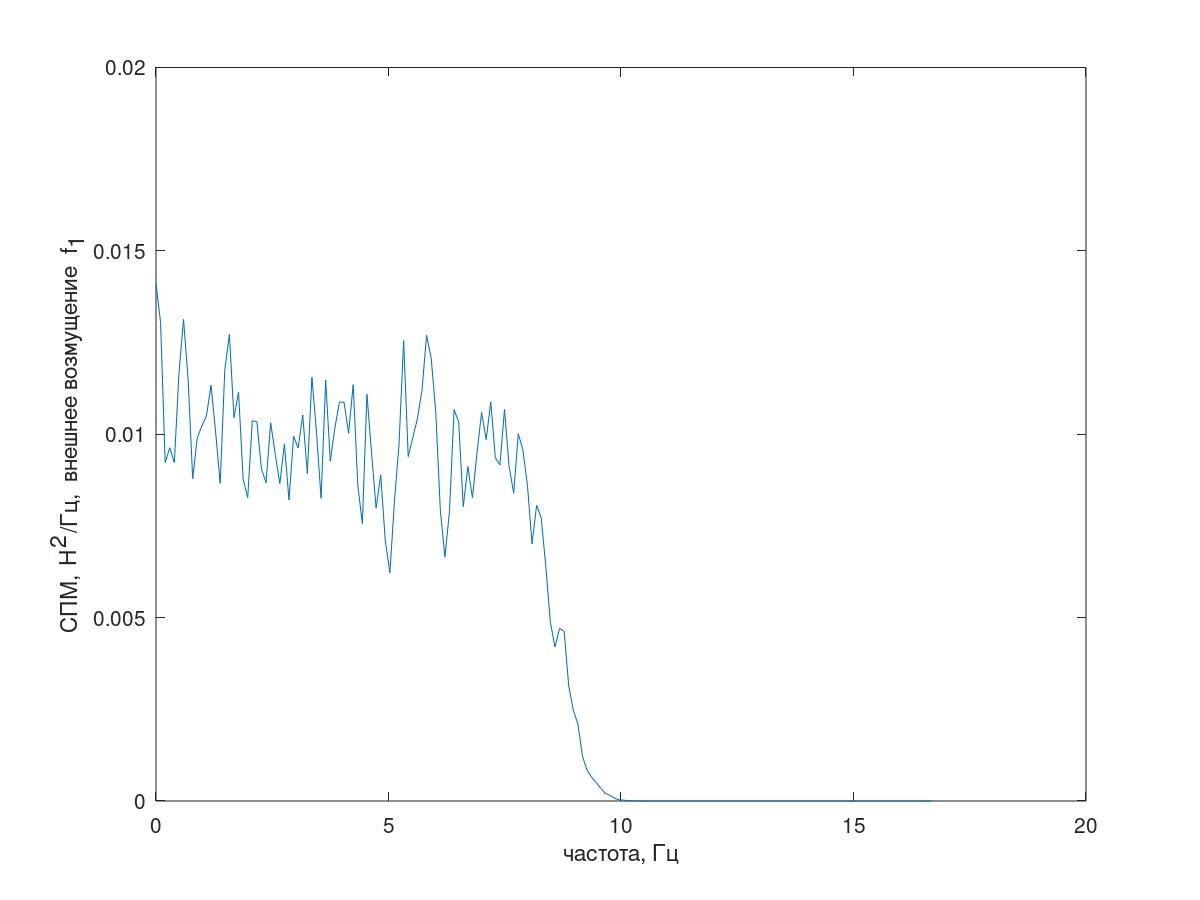Fig. 3 Espectro de perturbaciones externas.
En la figura 4 se muestra un fragmento de la implementación temporal de la perturbación.
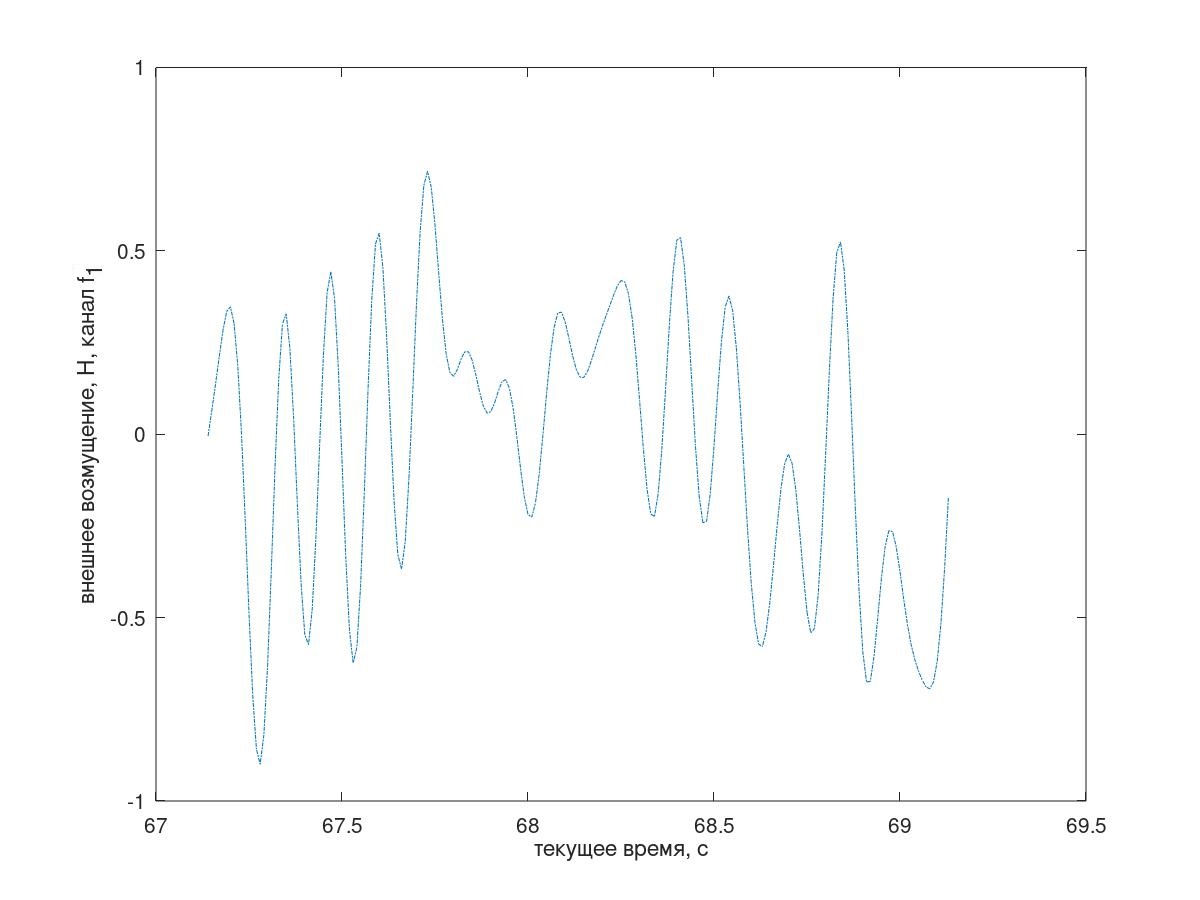
Fig. 4 Un fragmento de la implementación temporal de la perturbación entrante
En tiempo continuo, el modelo es un sistema de ecuaciones de difusión (6),
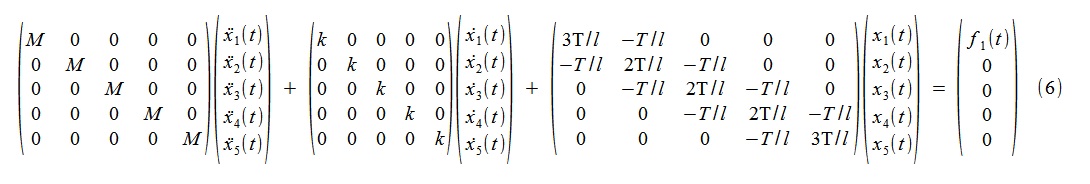
donde M = 1 kg, k = 10 kg / s, T = 2000N, l = 1 m.
Las matrices correspondientes (está claro cuáles) son numéricamente iguales a las siguientes:
Una de las respuestas de frecuencia del sistema se muestra en la figura 5.
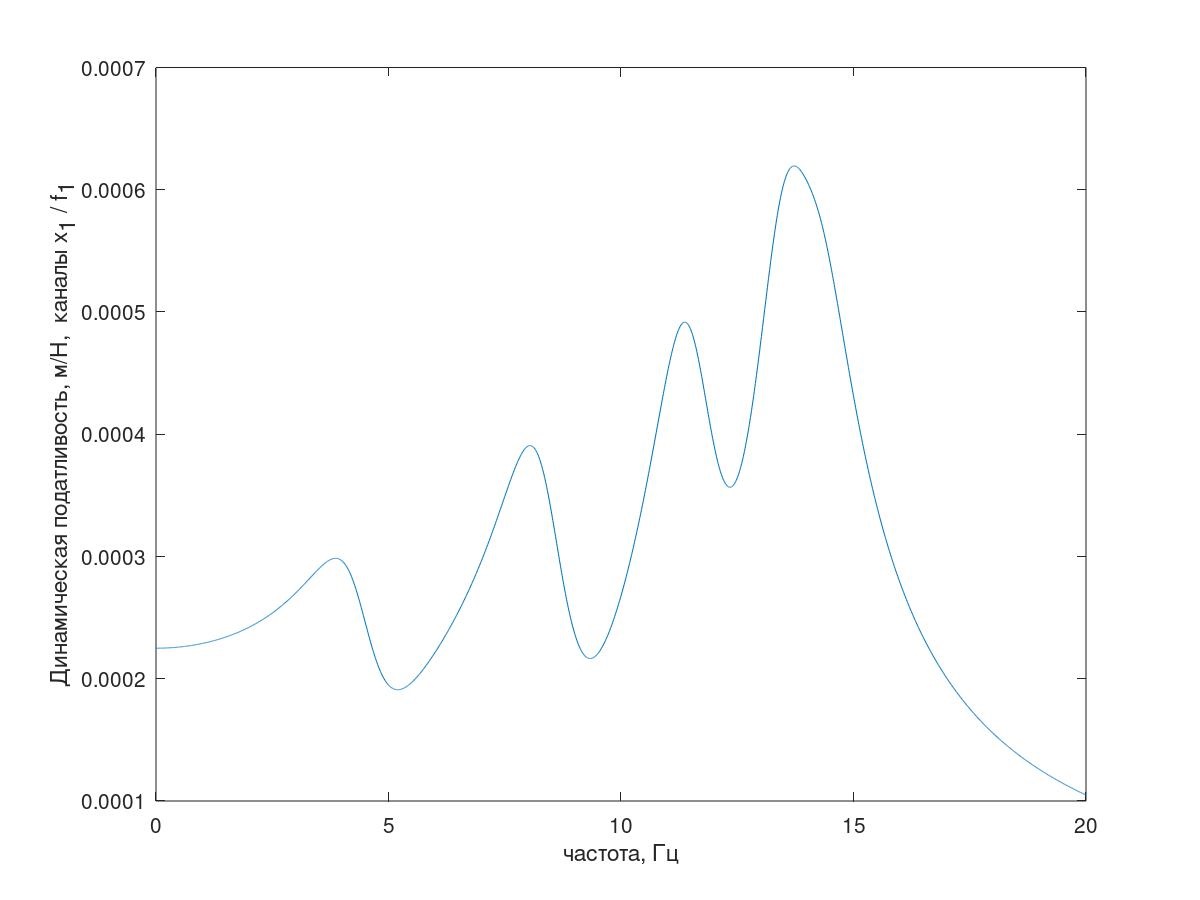Fig.5. Respuesta de frecuencia del sistema de prueba.(Explicación: todo está en orden con el número de picos resonantes, ya que en la figura 5 se muestra una explicación de esta respuesta de frecuencia del sistema con amortiguamiento reducido condicionalmente (k = 1 kg / s).
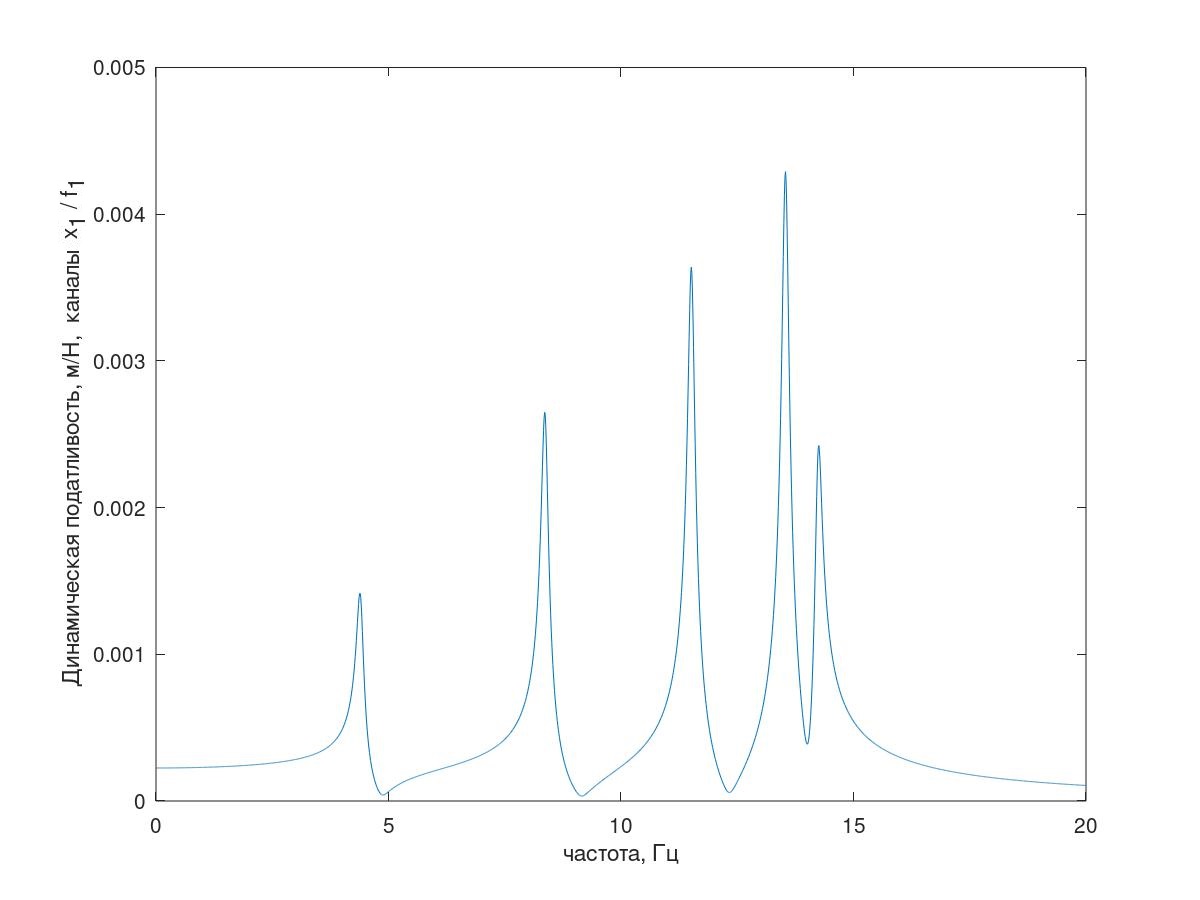Fig. 6 Explicación de cinco resonancias.
Para la simulación en tiempo discreto, se utiliza un modelo de diferencia finita (los modelos Raman funcionan bien en pequeños intervalos de muestreo, como
se mostró ).
Una pequeña digresión. Algún tiempo después, en el marco de otro trabajo, se realizó el modelado por diferencias finitas de este sistema de prueba por otros medios (Xcos \ Simulink). Matemáticamente, los modelos son idénticos. Se obtuvieron imágenes animadas de la respuesta del sistema a un solo impulso en el nodo No 1 y el nodo No 3. Los resultados son interesantes aquí desde el punto de vista de la verificación del modelo de diferencias finitas.
(El almacenamiento en búfer "impredecible" de los marcos de software libre estropea un poco las imágenes, especialmente la segunda, pero, en principio, el resultado es muy bueno).
Pero volvamos a nuestro modelo Matlab (GNUOctave). El espectro de respuesta resultante se muestra en la figura 7.
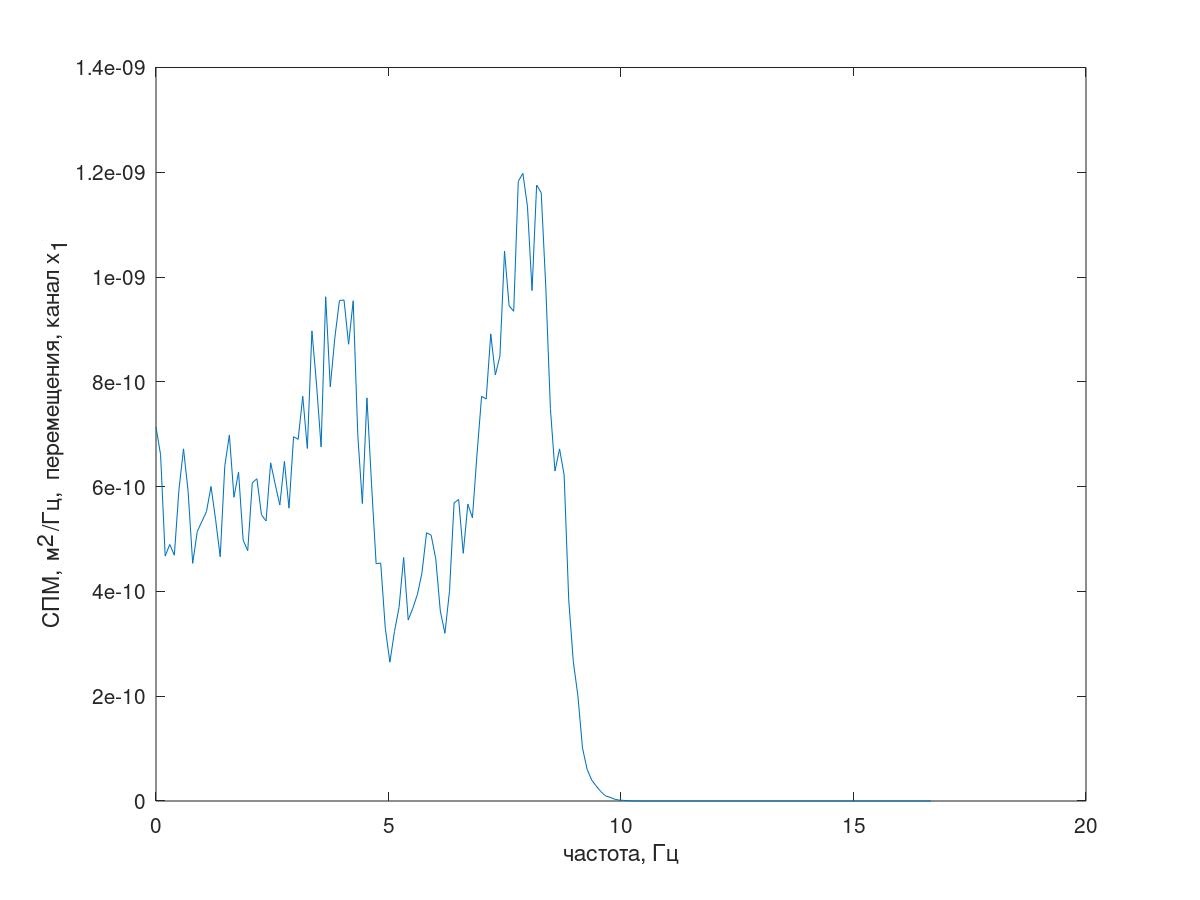Fig. 7 Espectro de respuesta (canal x 1 )Además, el método de correlación se utilizó para encontrar los valores de las correlaciones automáticas y cruzadas de los canales de respuesta.
Los resultados de la aplicación del método en discusión: se encontraron variaciones de los procesos pseudo-modales Rqq y formas pseudo-distintas de H:
Los primeros tres procesos en la descomposición, la animación de todo el proceso multicanal y los primeros tres modos de vibración correspondientes en 32 muestras (de 6714 a 6746 muestras, es decir, de 67.13 s en términos de cantidad) son aparentemente cuantitativamente significativas (por los valores de sus dispersiones en Rqq) 67.63 s hora actual) se muestra en la Fig. 1 al comienzo del artículo. Como puede ver, estas pseudoformas tienen algunas similitudes con sus propias formas de vibraciones de cuerda.
La experiencia acumulada indica las siguientes características de este método.
- El método es sensible al ruido extraño, que incluye alta frecuencia Existe el peligro de obtener resultados "aleatorios" (con un gran error aleatorio) y la aparente irreproducibilidad de los resultados experimentales. Es necesario filtrar cuidadosamente la parte que no funciona (cuantitativamente insignificante) del rango de frecuencia de la señal multicanal. (En un momento, el trabajo en esta dirección incluso se detuvo debido a informes de experimentadores sobre la "ausencia" de correlación entre canales, el efecto de un fuerte ruido)
- Los mejores resultados se obtuvieron con el número de canales de observación significativamente mayor que el número de manifestaciones esperadas de formas vibratorias (el número de picos resonantes en el rango estudiado), es decir. para m << n.
- Con factores Q altos, los sistemas de pseudoformas parecen tender a los verdaderos modos intrínsecos del sistema. Los resultados obtenidos en tales sistemas son más estables en caso de ruido.
- Si el par de valores propios Rxx [0] coincide o incluso converge, el par de las pseudoformas correspondientes aparentemente se determina hasta sus combinaciones lineales independientes; tales formas no se pueden separar entre sí en condiciones experimentales dadas.
- Aparentemente, al comparar las formas verdaderas (encontradas por otros métodos) y las seudoformas consideradas, con cierta probabilidad es posible encontrar los puntos de aplicación de la perturbación externa (especialmente con una perturbación de canal pequeño), si tal problema es relevante.