Introduccion
La palabra inglesa wavelet (del francés "ondelette") se traduce literalmente como "onda corta (pequeña)". En varias traducciones de artículos extranjeros al ruso, también hay términos: "ráfaga", "función de ráfaga", "función de onda baja", "onda", etc.
La transformación Wavelet (VP) se usa ampliamente para el análisis de señales. Además, encuentra una gran aplicación en el campo de la compresión de datos. El VP de una señal unidimensional es su representación en forma de serie generalizada o integral de Fourier sobre un sistema de funciones básicas.
psiab(t)= frac1 sqrta psi left( fract−ba right) , (1)
construido a partir de la wavelet madre (fuente)
psi(t) que posee ciertas propiedades debido a operaciones de cambio de tiempo (b) y cambios de escala temporal (a).
Multiplicador
1/ sqrta garantiza la independencia de la norma de funciones (1) del número de escala (a). Para los valores dados de los parámetros a y b, la función
psiab(t) y hay una wavelet generada por la wavelet madre
psi(t) .
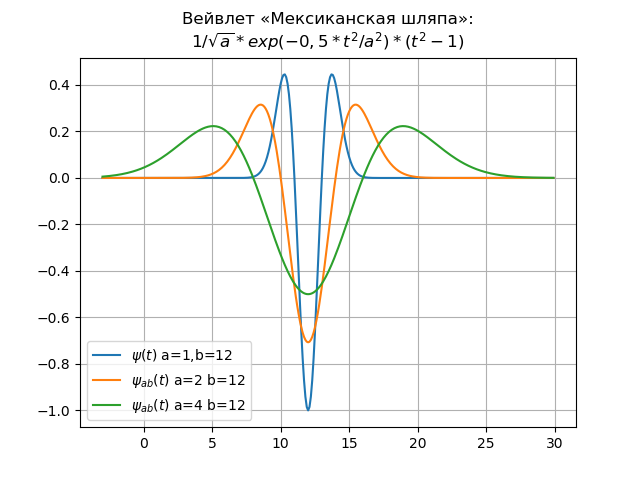
Un ejemplo es la ola mexicana del sombrero en los dominios de tiempo y frecuencia:
Listado de wavelet para dominio de tiempofrom numpy import* import matplotlib.pyplot as plt x= arange(-4,30,0.01) def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f plt.title(" « »:\n$1/\sqrt{a}*exp(-0,5*t^{2}/a^{2})*(t^{2}-1)$") y=[w(1,12,t) for t in x] plt.plot(x,y,label="$\psi(t)$ a=1,b=12") y=[w(2,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=2 b=12") y=[w(4,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=4 b=12") plt.legend(loc='best') plt.grid(True) plt.show()
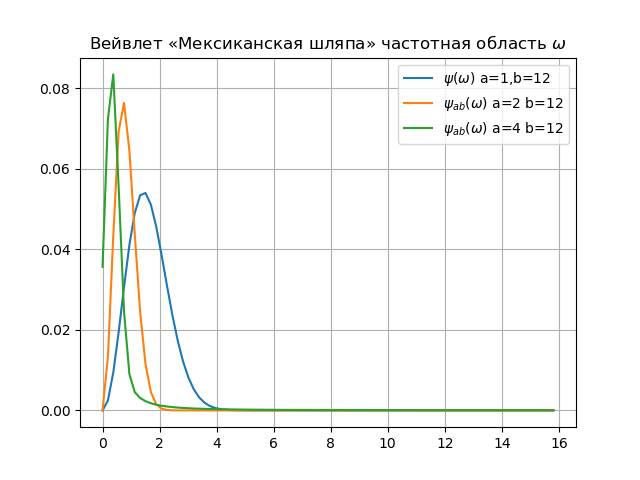
Listado para el espectro wavelet from numpy import* from pylab import * from scipy import * import os def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f x= arange(-4,30,0.2) def plotSpectrum(y,Fs): n = len(y) k = arange(n) T = n/Fs frq = k/T frq = frq[range(int(n/2))] Y = fft(y)/n Y = Y[range(int(n/2))] return Y,frq xlabel('f (Hz)') ylabel('|Y(f)|') Fs=1024.0 y=[w(1,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi(\omega)$ a=1,b=12") y=[w(2,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=2 b=12") y=[w(4,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=4 b=12") plt.title(" « » $\omega$") legend(loc='best') grid(True) show()
 Conclusión
Conclusión1. Entre el concepto de armónicos de Fourier y la escala de la wavelet, realmente existe una relación. Lo principal en esta relación es la proporción inversa de la frecuencia y escala natural. Además, al reducir la escala, aumentamos el ancho de banda del espectro wavelet.
2. Al cambiar la escala (el aumento de un conduce a un estrechamiento del espectro de Fourier de la función
psiab(t) ), las wavelets pueden detectar la diferencia de características en diferentes escalas (frecuencias) y, debido al cambio, analizar las propiedades de la señal en diferentes puntos en todo el intervalo estudiado. Por lo tanto, al analizar señales no estacionarias, debido a la localidad de las wavelets, obtienen una ventaja significativa sobre la transformada de Fourier, que proporciona solo información global sobre las frecuencias (escalas) de la señal analizada, ya que el sistema de funciones utilizado (el exponente complejo o senos y cosenos) se define en intervalo infinito
3. Los listados anteriores escritos en el lenguaje Python de alto nivel distribuido libremente le permiten seleccionar funciones para wavelets que cumplan con los requisitos especificados. Sin embargo, también es necesario tener en cuenta todos los signos principales de las wavelets.
Los principales signos de la wavelet.
Limitación El cuadrado de la norma de la función debe ser finito:
left | psi right |2= int infty− infty left| psi(t) right|2dt< infty . (2)
Localización VP, en contraste con la transformada de Fourier, utiliza una función inicial localizada tanto en tiempo como en frecuencia. Para hacer esto, es suficiente que se cumplan las siguientes condiciones:
left| psi(t) right| leqC(1+ left|t right|)−1− varepsilon y
left|S psi( omega) right| leqC(1+ left| omega right|)−1− varepsilon a las
varepsilon>0 , (3)
Por ejemplo, una función delta
delta(t) y la función armónica no satisfacen la condición necesaria para la localización simultánea en los dominios de tiempo y frecuencia.
Promedio cero El gráfico de la función original debe oscilar (alternarse) alrededor de cero en el eje de tiempo y tener un área cero:
int infty− infty psi(t)dt=0 . (4)
A partir de esta condición, queda claro la elección del nombre "wavelet" - una pequeña ola.
Área de función igual a cero
psi(t) es decir momento cero, lleva al hecho de que la transformada de Fourier
S psi( omega) esta función es igual a cero para
omega=0 y tiene la forma de un filtro de paso de banda. Para varios valores (a), este será un conjunto de filtros de paso de banda.
A menudo, para las aplicaciones, es necesario que no solo cero, sino todos los primeros n momentos sean iguales a cero:
int infty− inftytn psi(t)dt=0 . (5)
Las n-ésimas ondas permiten analizar la estructura más fina (alta frecuencia) de la señal, suprimiendo sus componentes que cambian lentamente.
Hecho a sí mismo. Un rasgo característico de VP es su autosimilitud. Todas las wavelets de una familia específica.
psiab(t) tener el mismo número de oscilaciones que la wavelet madre
psi(t) , ya que se obtiene de él mediante transformaciones de escala (a) y desplazamiento (b).
Transformada continua de wavelet
Transformación wavelet continua (integral) (NVP o WT - transformada wavelet continua). Construimos la base
psiab(t) usando transformaciones continuas de escala (a) y transferencias (b) de la wavelet madre
psi(t) con valores arbitrarios de los parámetros básicos ayb en la fórmula (1).
Luego, por definición, el NVP directo (análisis) e inverso (síntesis) (es decir, PNVP y ONVP) de la señal S (t) se escriben de la siguiente manera:
Ws(a,b)=(S(t), psiab(t))= frac1 sqrta int infty− inftyS(t) psi left( fractba right)dt , (6)
S(t)= frac1C psi int infty− infty int infty− inftyWs(a,b) psiab(t) fracdadba2 , (7)
donde
C psi - coeficiente de normalización,
C psi= int infty− infty left| psi( omega) right|2 left| omega right|−1d omega< inftydonde: (•, •) es el producto escalar de los factores correspondientes,
mathbf psi( omega) - Transformada de Fourier de una wavelet
psi(t) . Para wavelets ortonormales
C psi=1 .
De (6) se desprende que el espectro wavelet
Ws(b,a) (espectro wavelet, o espectro de escala de tiempo), a diferencia del espectro de Fourier (espectro único), es una función de dos argumentos: el primer argumento a (escala de tiempo) es similar al período de oscilación, es decir es inverso a la frecuencia, y el segundo b –– es similar al desplazamiento de la señal a lo largo del eje de tiempo.
Cabe señalar que
Ws(b,a0) caracteriza la dependencia del tiempo (en
a=a0) , mientras que las dependencias
Ws(a,b0) es posible igualar la dependencia de frecuencia (para
b=b0 )
Si la señal estudiada S (t) es un pulso único de duración
tauu concentrado en el barrio
t=t0 , entonces su espectro wavelet tendrá el mayor valor en la vecindad del punto con coordenadas
a= tauu,b=t0 .
Métodos de presentación Ws(b,a) puede ser diferente Espectro
Ws(b,a) Es una superficie en el espacio tridimensional. Sin embargo, a menudo en lugar de la imagen de la superficie, su proyección en el plano ab se presenta con niveles iso (o figuras de varios colores), que permiten rastrear el cambio en la intensidad de las amplitudes EP en diferentes escalas (a) y en el tiempo (b).
Además, representan líneas de extremos locales de estas superficies, el llamado esqueleto (sceleton), que revela la estructura de la señal analizada.
Transformación de wavelet continua al determinar el espectro de wavelet basado en la wavelet madre - "sombrero mexicano".
También se usan otras wavelets maternas para NVP:

VP continuo es ampliamente utilizado en el procesamiento de señales. En particular, el análisis wavelet (VA) brinda oportunidades únicas para reconocer características locales y "sutiles" de señales (funciones), lo cual es importante en muchas áreas de la ingeniería de radio, comunicaciones, electrónica de radio, geofísica y otras ramas de la ciencia y la tecnología. Consideremos esta posibilidad con algunos ejemplos simples.
Oscilación armónica.La señal tiene la forma:
s(t)=Asin( omegat− phi)donde:
A=1V, omega= frac2 piT= frac2 pi50, psi=0Función de formación de ondas:
MHAT(t):= fracd2dt2exp(−t2/2) ,
Wavelets:
psi(a,b,t)= frac1 sqrtaMHAT left( fract−ba right) ,
Espectro de ondículas: N: = 256, a: = 1..30, b: = 0..50,
W(a,b):= intN−N psi(a,b,t)s(t)dt,Nab:=W(a,b). .
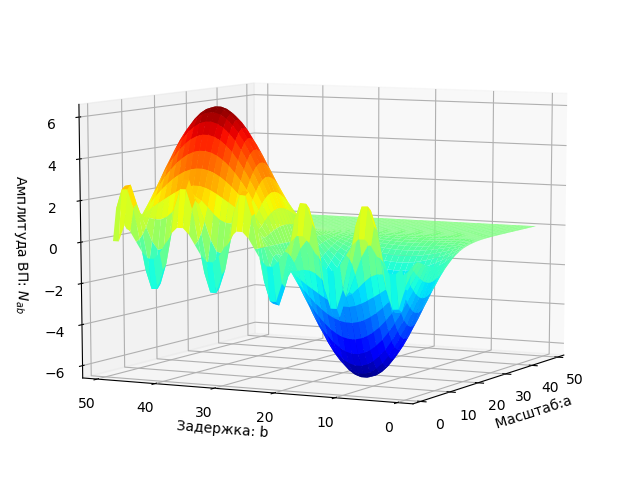
Listado de programa from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 T=50 def S(t): return sin(2*pi*t/T) plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,100,1)] x=[t for t in arange(0,100,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49,49) fig = plt.figure("- : ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
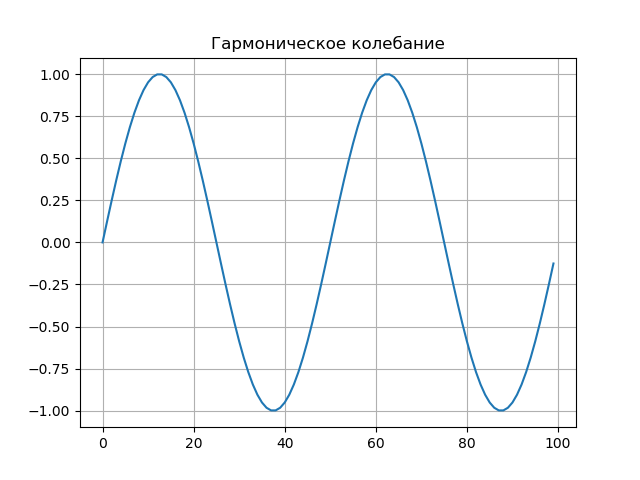
Gráfico de señal

Gráfico de un espectro de dos parámetros.
Nab=W(ab) se muestra como una superficie en un espacio tridimensional.

Cabe señalar que la sección W (a, b) para la escala de tiempo
a=a0 caracteriza la oscilación inicial s (t). Además, su amplitud es máxima en
a0:1/ omega . Dependencias
W(a0,b0) puede coincidir con el espectro actual de oscilaciones en
b=b0 .
La suma de dos oscilaciones armónicas.La señal tiene la forma:
s(t):=A1sin( omega1t)+A2sin( omega2t)donde:
A1=A2=1V, omega1= frac2 piT1, omega2= frac2 piT2,T1=50s,T2=10s .
MHAT(t):= fracd2dt2 left[e−t2/2 right] , N: = 256,
psi(a,b,t):=MHAT left( fractba right),W(a,b):= intN−N psi(a,b,t)f(t)dt , a: = 1 ... 30, b: = 0 ... 50,
Nab:=W(a,b) .
Listado de programa from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): return sin(2*pi*t/10)+sin(2*pi*t/50) plt.figure(' ') plt.title(' ', size=12) y=[S(t) for t in arange(0,250,1)] x=[t for t in arange(0,250,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49, 49) fig = plt.figure("-:2- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z, 100) plt.figure() q=[w(2,i) for i in y] p=[i for i in y] plt.plot(p,q,label='w(2,b)') q=[w(15,i) for i in y] plt.plot(p,q,label='w(15,b)') q=[w(30,i) for i in y] plt.plot(p,q,label='w(30,b)') plt.legend(loc='best') plt.grid(True) plt.figure() q=[w(i,13) for i in x] p=[i for i in x] plt.plot(p,q,label='w(a,13)') q=[w(i,17) for i in x] plt.plot(p,q,label='w(a,17)') plt.legend(loc='best') plt.grid(True) plt.show()

Gráfico de señal
La gráfica del espectro de dos parámetros W (a, b) se muestra como una superficie en un espacio tridimensional.
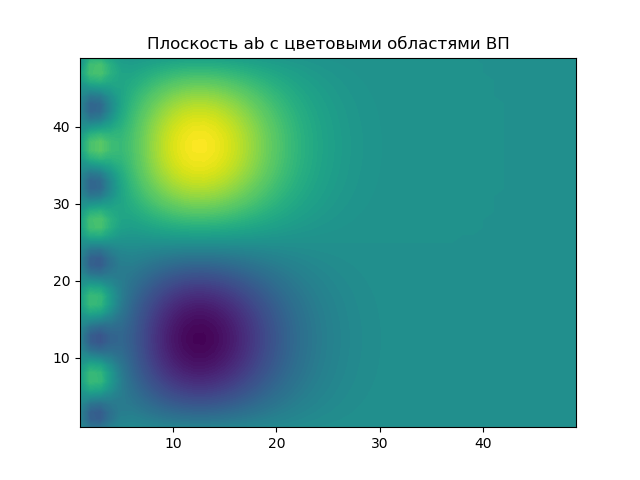
El plano de los parámetros a, b en el que los resultados del EP se resaltan en áreas coloreadas.

El gráfico muestra las "secciones transversales" del espectro wavelet para dos valores del parámetro a. Con un parámetro relativamente pequeño de la escala de tiempo a, para
a1=2(a1:1/ omega2) , la sección transversal del espectro lleva información solo sobre el componente de alta frecuencia de la señal, filtrando (suprimiendo) su componente de baja frecuencia.
A medida que aumenta, la extensión de la función base
psi( fract−ba) , por lo tanto, reduciendo su espectro y reduciendo el ancho de banda de la "ventana" de frecuencia. Como resultado, cuando
a2=15(a2:1/ omega1) La sección transversal del espectro es solo un componente de baja frecuencia de la señal.
Con un aumento adicional en a, la banda de la ventana todavía disminuye y el nivel de este componente de baja frecuencia disminuye a un componente constante (para a> 25), que es igual a cero para la señal analizada.

El gráfico muestra las secciones del espectro wavelet W (a, b) que caracterizan
espectro de señal actual en
b1=13 y
b2=17 . El espectro de la señal considerada, en contraste con el armónico, contiene un componente de alta frecuencia en la región de valores pequeños de la escala de tiempo a (a: 1..3), que corresponde al segundo componente de la señal
A2sin( omega2t) .
Momento rectangular.U:=5,t0:=20, tau:=60s(t):= beginvmatrixU,sit0 leqt leqt0+ tau0,delocontrario endvmatrixMHAT(t):= fracd2dt2exp left( frac−t22 right)N:=128, psi(a,b,t):=MHAT left( fractba right),W(a,b):= intN−N psi(a,b,t)f(t)dta:=1..50,b:=0..100,Nba:=W(a,b)Listado de programa from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): U=5;t0=20;tau=60 if t0<=t<=t0+tau: return U else: return 0 plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,120,1)] x=[t for t in arange(0,120,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,100,1) y = arange(1,100,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(99, 99) fig = plt.figure("3D- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
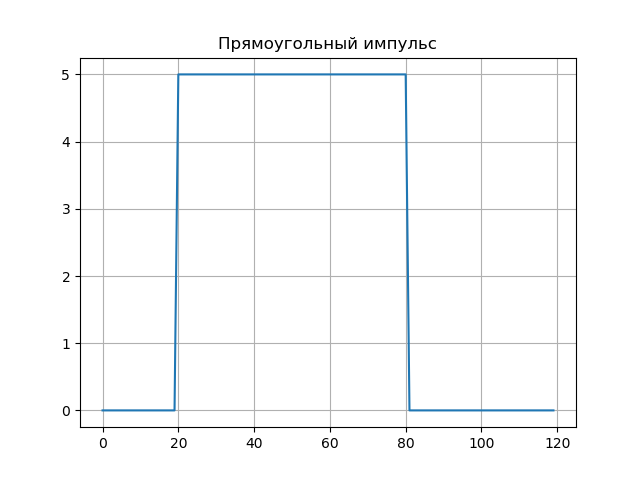


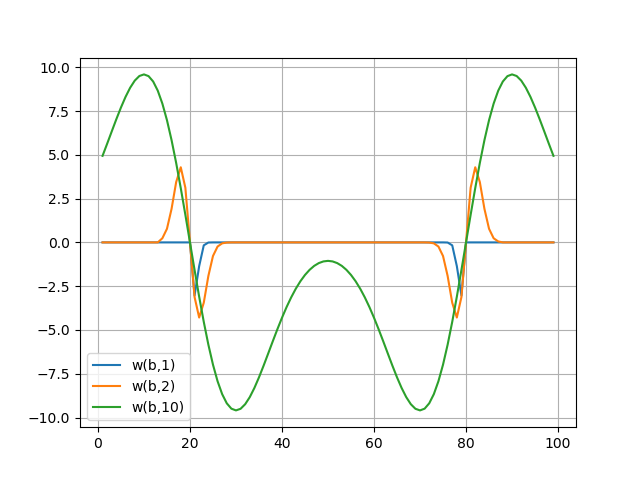
Los espectros wavelet se muestran en gráficos, el espectro wavelet transmite bien las características sutiles de la señal: sus saltos en las muestras b = 20 y b = 80 (para a: 1..10).
Conclusiones
Esta publicación es de naturaleza educativa, proporciona información básica sobre el análisis wavelet en general, y ejemplos simples en el lenguaje de programación de alto nivel distribuido libremente Python muestran las características del análisis wavelet continuo con una amplia visualización gráfica en 3D y 2D.
PD: El autor no resta ventajas incondicionales al análisis de wavelets utilizando Matlab tanto en términos de número de wavelets como de velocidad. Pero en Python todavía hay espacio para un mayor desarrollo: scipy.signal y PyWavelets.