Todos en la industria de TI saben lo difícil que es evaluar la fecha límite de un proyecto. Es difícil evaluar objetivamente cuánto tiempo llevará resolver una tarea difícil. Una de mis teorías favoritas es que esto es solo un artefacto estadístico.

Supongamos que evalúa un proyecto a la semana 1. Supongamos que hay tres resultados igualmente probables: o tomará 1/2 semana, o 1 semana, o 2 semanas. El resultado medio es en realidad el mismo que el estimado: 1 semana, pero el valor promedio (también conocido como promedio, también conocido como valor esperado) es 7/6 = 1.17 semanas. El puntaje está realmente calibrado (imparcial) para la mediana (que es 1), pero no para el promedio.

Un modelo razonable para el "factor de inflación" (tiempo real dividido por tiempo estimado) sería algo así como una distribución lognormal . Si la estimación es igual a una semana, simulamos el resultado real como una variable aleatoria distribuida de acuerdo con la distribución lognormal durante aproximadamente una semana. En tal situación, la mediana de la distribución es exactamente una semana, pero el valor promedio es mucho mayor:



Si tomamos el logaritmo del coeficiente de inflación, obtenemos una distribución normal simple con un centro de aproximadamente 0. Esto supone un coeficiente de inflación medio de 1x y, como espera, recuerde, log (1) = 0. Sin embargo, en varios problemas puede haber diferentes incertidumbres alrededor de 0. Podemos modelarlos cambiando el parámetro σ, que corresponde a la desviación estándar de la distribución normal:



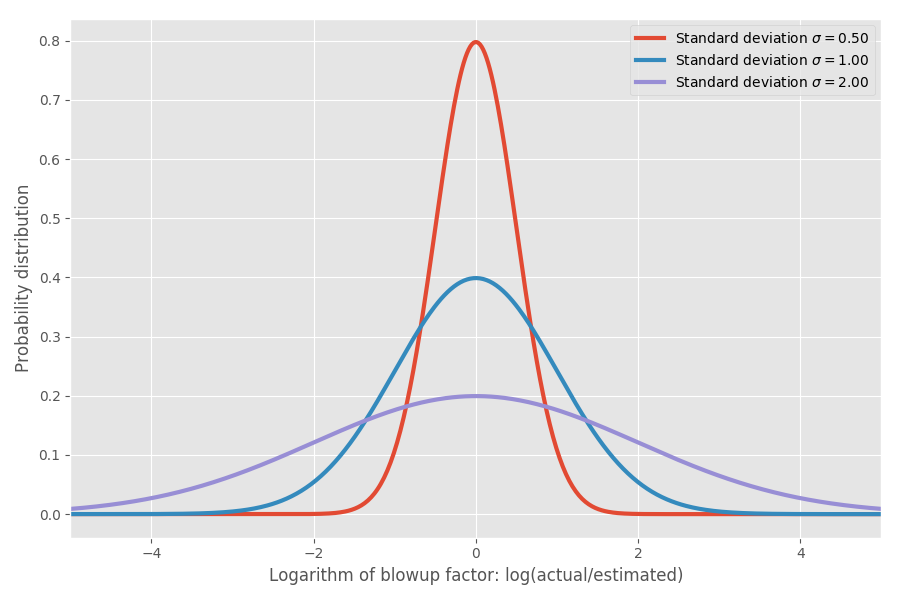
Solo para mostrar los números reales: cuando log (real / estimado) = 1, entonces el coeficiente de inflación exp (1) = e = 2.72. Es igualmente probable que el proyecto se extienda a exp (2) = 7.4 veces, y que termine en exp (-2) = 0.14, es decir, 14% del tiempo estimado. Intuitivamente, la razón por la que el promedio es tan grande es porque las tareas que se ejecutan más rápido de lo esperado no pueden compensar las tareas que toman mucho más tiempo de lo esperado. Estamos limitados a 0, pero no limitados en la otra dirección.

¿Es esto solo un modelo? ¡Ojalá pudieras! Pero pronto llegaré a los datos reales y en algunos datos empíricos demostraré que, de hecho, es bastante consistente con la realidad.

Estimación de cronogramas de desarrollo de software

Hasta ahora, todo bien, pero intentemos comprender lo que esto significa en términos de estimación de cronogramas de desarrollo de software. Supongamos que miramos un plan de 20 proyectos de software diferentes y tratamos de evaluar cuánto tiempo llevará completarlos.

Aquí es donde la media se vuelve decisiva. Los promedios se suman, pero no hay mediana. Por lo tanto, si queremos tener una idea de cuánto tiempo llevará completar la suma de N proyectos, debemos analizar el valor promedio. Supongamos que tenemos tres proyectos diferentes con el mismo σ = 1:


Tenga en cuenta que los promedios se suman y 4.95 = 1.65 * 3, pero otras columnas no.

Ahora agreguemos tres proyectos con diferente sigma:


Los promedios todavía están tomando forma, pero la realidad ni siquiera está cerca de la ingenua estimación de 3 semanas que podría haber esperado. Tenga en cuenta que un proyecto altamente incierto con σ = 2 domina el resto en el tiempo promedio de finalización. Y para el percentil 99, no solo domina, sino que literalmente absorbe a todos los demás. Podemos dar un ejemplo más amplio:


Nuevamente, la única tarea desagradable es principalmente dominante en el cálculo de la estimación, al menos para el 99% de los casos. Incluso en el tiempo promedio, un proyecto loco lleva aproximadamente la mitad del tiempo dedicado a todas las tareas, aunque tienen valores similares en términos de mediana. Por simplicidad, supuse que todas las tareas tienen la misma estimación de tiempo, pero diferentes incertidumbres. Las matemáticas se guardan cuando cambian los términos.

Es divertido, pero hace mucho que tengo este sentimiento. Agregar clasificaciones rara vez funciona cuando tienes muchas tareas. En cambio, descubra qué tareas tienen la mayor incertidumbre: estas tareas generalmente dominarán el tiempo promedio de ejecución.

El diagrama muestra la media y el percentil 99 en función de la incertidumbre (σ):



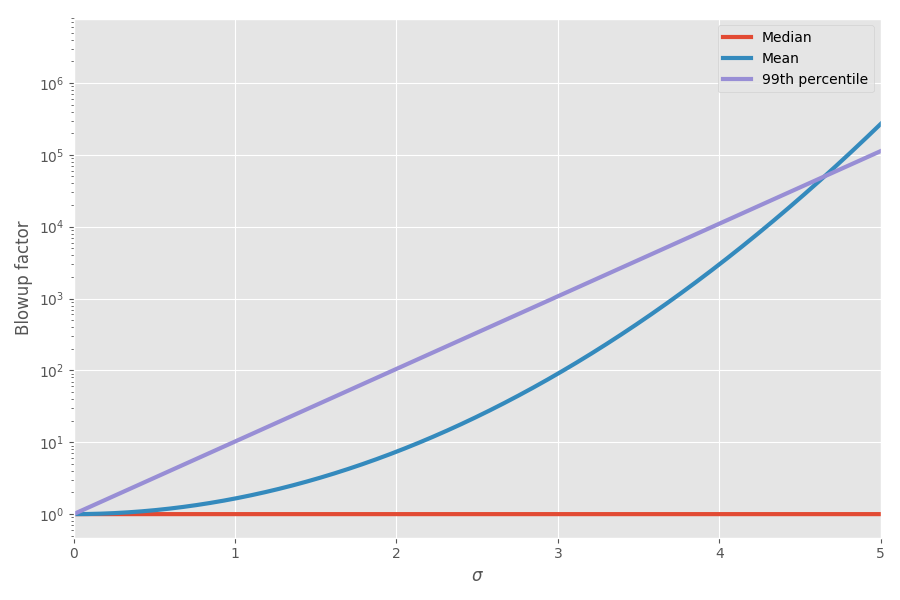
¡Ahora las matemáticas explicaron mis sensaciones! Comencé a tener esto en cuenta al planificar proyectos. Realmente creo que agregar estimaciones de los plazos para las tareas es muy engañoso y crea una imagen falsa de cuánto tiempo tomará todo el proyecto, porque tienes estas locas tareas sesgadas que finalmente toman todo el tiempo.

¿Dónde está la evidencia empírica?

Durante mucho tiempo lo mantuve en mi cerebro en la sección "modelos de juguetes curiosos", a veces pensando que esta es una buena ilustración del fenómeno del mundo real. Pero un día, deambulando por la red, me topé con un conjunto interesante de datos para evaluar el momento de los proyectos y el tiempo real para completarlos. Ficcion!

Hagamos un gráfico de dispersión rápida del tiempo estimado y real:



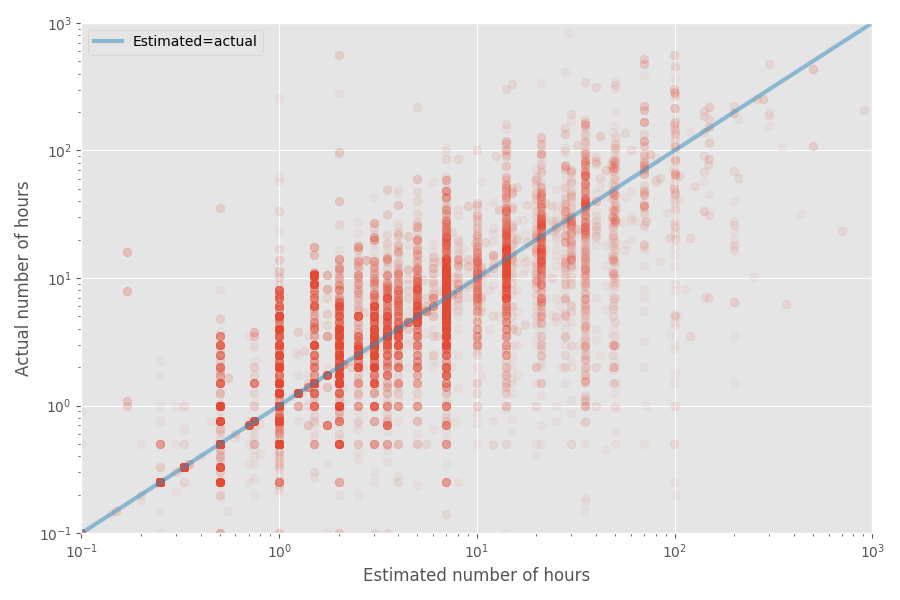
La tasa de inflación media para este conjunto de datos es 1X, mientras que el coeficiente promedio es 1.81x. Nuevamente, esto confirma el presentimiento de que los desarrolladores califican bien la mediana, pero el promedio es mucho más alto.

Veamos la distribución del coeficiente de inflación (logaritmo):



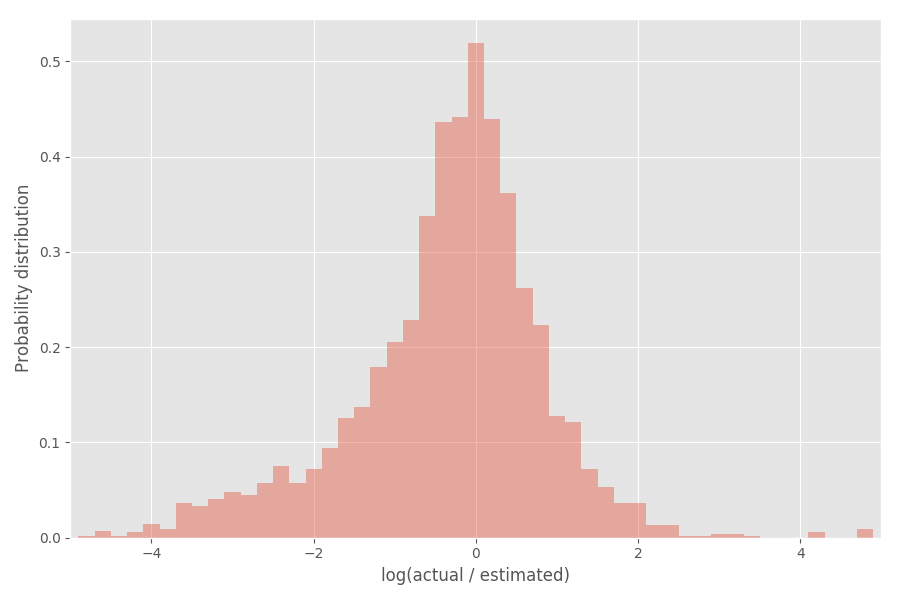
Como puede ver, está bastante bien centrado alrededor de 0, donde el coeficiente de inflación exp (0) = 1.

Toma las herramientas estadísticas

Ahora voy a soñar un poco con las estadísticas. No dude en omitir esta parte si no le resulta interesante. ¿Qué podemos concluir de esta distribución empírica? Puede esperar que los logaritmos de la tasa de inflación se distribuyan de acuerdo con la distribución normal, pero esto no es del todo cierto. Tenga en cuenta que σ en sí es aleatorio y varía para cada proyecto.

Una forma conveniente de modelar σ es que se seleccionan de la distribución gamma inversa . Si suponemos (como antes) que el logaritmo de los coeficientes de inflación se distribuye de acuerdo con la distribución normal, entonces la distribución "global" de los logaritmos de los coeficientes de inflación termina con la distribución de Student .

Aplicamos la distribución del alumno a la anterior:



Decente converge, en mi opinión! Los parámetros de distribución de los estudiantes también determinan la distribución gamma inversa de los valores de σ:



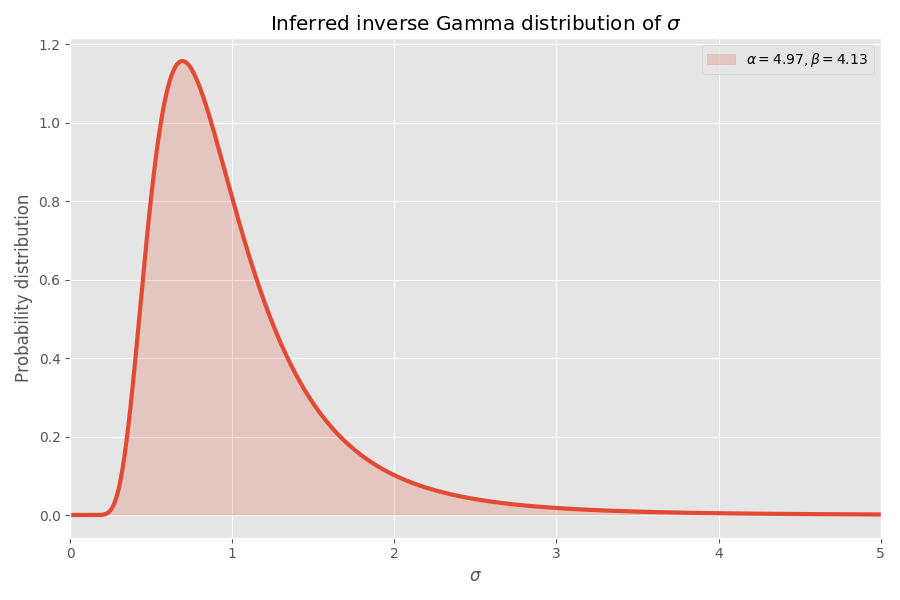
Tenga en cuenta que los valores de σ> 4 son muy poco probables, pero cuando ocurren, causan una explosión promedio de varios miles de veces.

Por qué las tareas de software siempre toman más tiempo de lo que piensas

Suponiendo que este conjunto de datos sea representativo del desarrollo de software (¡dudoso!), Podemos sacar algunas conclusiones más. Tenemos parámetros para la distribución de Estudiantes, por lo que podemos calcular el tiempo promedio requerido para completar la tarea sin conocer σ para esta tarea.

Si bien la tasa de inflación media de este ajuste es 1x (como antes), la tasa de inflación del 99% es 32x, pero si va al percentil 99.99, ¡son la friolera de 55 millones ! Una interpretación (gratuita) es que algunas tareas son en última instancia imposibles. De hecho, estos casos extremos tienen un impacto tan grande en el promedio que la tasa de inflación promedio de cualquier tarea se vuelve infinita . ¡Estas son noticias bastante malas para cualquiera que intente cumplir con los plazos!

Resumen

Si mi modelo es correcto (grande si), entonces esto es lo que podemos descubrir:

• Las personas estiman bien el tiempo medio para completar una tarea, pero no el promedio.
  
• El tiempo promedio es mucho mayor que la mediana debido al hecho de que la distribución está distorsionada (distribución lognormal).
  
• Cuando agrega calificaciones para n tareas, las cosas empeoran.
  
• Las tareas de mayor incertidumbre (más bien, de mayor tamaño) a menudo pueden dominar en el tiempo promedio requerido para completar todas las tareas.
  
• El tiempo promedio de ejecución de una tarea de la que no sabemos nada es en realidad infinito .

Notas

• Obviamente, los resultados se basan en un solo conjunto de datos que encontré en Internet. Otros conjuntos de datos pueden dar resultados diferentes.
  
• Mi modelo, por supuesto, también es muy subjetivo, como cualquier modelo estadístico.
  
• Me encantaría aplicar el modelo a un conjunto de datos mucho más grande para ver qué tan estable es.
  
• Sugerí que todas las tareas son independientes. De hecho, pueden tener una correlación que hará que el análisis sea mucho más molesto, pero (creo) terminar con conclusiones similares.
  
• La suma de los valores distribuidos lognormalmente no es otro valor distribuido lognormalmente. Esta es la debilidad de esta distribución, ya que puede argumentar que la mayoría de las tareas son simplemente la suma de las subtareas. Sería bueno si nuestra distribución fuera sostenible .
  
• Eliminé pequeñas tareas del histograma (el tiempo estimado es menor o igual a 7 horas), ya que distorsionan el análisis y hubo una oleada extraña de exactamente 7.
  
• El código está en Github , como siempre.