Buenas tardes, querido lector! Este es el segundo artículo traducido en una serie de artículos sobre la creación del motor de física por Chris Hecker. Si aún no se ha familiarizado con el primero , le recomiendo hacerlo, porque todo se aclarará de inmediato. Muchas gracias por apoyar la primera traducción: ¡es muy alentador trabajar más y más! Que tengas una buena lectura!

Física, Parte 2, Efectos Angulares

Solo quería retroceder la puerta con algo pesado para que no entrara un intruso. ¿Estoy preguntando mucho? Quiero que su auto se voltee y explote en un lugar específico. Quiero que los enormes engranajes se atasquen antes de aplanarme. Y quiero construir apresuradamente una cosa que parece un columpio, para catapultar un lindo regalo brillante a través de la pared de la fortaleza del castillo. ¿Quién puede evitar que traduzca todo esto en realidad? Asumes que mi oponente está en el mundo del juego, pero en realidad, un programador del motor físico, porque todo lo anterior se basa en el efecto angular. Puede contar con los dedos aquellos juegos donde se implementan efectos de esquina, sin mencionar encontrar al menos uno en el que esto se hace correctamente.

La razón principal por la cual los efectos angulares (o de otro modo rotacionales) no se implementan en los juegos hoy en día es porque los programadores creen que la física que describe el movimiento rotacional es demasiado complicada para comprenderla y traducirla en realidad. En las clases de física en la escuela secundaria (donde todos aprendimos la segunda ley de Newton) por lo general no hablan de efectos de rotación, y no es del todo obvio cómo pasar de la fuerza aplicada al objeto a la rotación de este objeto. Por supuesto, la dinámica del movimiento de rotación es un poco más difícil de entender que la dinámica del movimiento lineal, pero es más simple de lo que parece. Cualquiera que pueda crear un motor físico de acuerdo con el material que se presenta en el primer artículo del ciclo también logrará incluir los efectos angulares descritos en este artículo. Se espera que después de la publicación de este artículo, el mundo se llene de juegos que utilicen todas las posibilidades y ventajas de los efectos de esquina, o al menos pueda crear un juego en el que, cuando se doble, dispare a su amigo en la pierna en una batalla mortal.

Breve repetición

A pesar del hecho de que cada uno de mis artículos sobre algún tema único, siempre releo lo que escribí antes, para entender dónde terminé. Acabo de ver mi primer artículo sobre física, y estoy encantado: ¡logramos aprender tanto y, además, nunca escribimos un código de programa ni leímos literatura adicional! Antes de comenzar, vamos a actualizar el material del último artículo.



La Tabla 1 contiene las conclusiones más importantes para la dinámica de los sólidos. De la ecuación 1 se deduce que el vector de coordenadas (r), el vector de velocidad (v) y el vector de aceleración (a) están relacionados por derivadas (y por integrales, si leemos en orden inverso). Como recordatorio, marcamos la diferenciación de tiempo por un primo (r '). r 'es lo mismo que dr / dt, y r' 'es lo mismo que la segunda derivada del tiempo. De la ecuación 2 se deduce que la fuerza está asociada con un momento lineal (el producto de la masa y la velocidad), la masa y la aceleración. La definición del centro de masa se puede obtener de la Ecuación 3 (este es el punto donde todas las masas y distancias se equilibran entre sí). La ecuación 4 establece que el momento lineal total de un sólido es la suma de todos sus momentos, que, para nuestra suerte, son simplemente iguales al momento del centro de masa (CM). La ecuación 5 es una verdadera joya. Utiliza la Ecuación 4 para demostrar que la aceleración del centro de masa de un objeto está relacionada con la fuerza total (el vector de la suma de todas las fuerzas que actúan sobre el objeto en un momento dado) a través de una cantidad escalar, la masa del objeto.

Para resumir todo lo descrito en el primer artículo: aprendimos que la fuerza total que actúa sobre nuestro centro de masa es igual a la suma de todas las fuerzas aplicadas al cuerpo (incluida la fuerza de gravedad, el carro del villano, una explosión cercana, el empuje de nuestro motor, etc. .). Después de eso, dividimos este vector suma por la masa corporal para obtener la aceleración CM, y luego integramos la aceleración de tiempo para obtener la velocidad y la coordenada del cuerpo.

¡La ecuación 5 es solo una obra maestra! Verá que en él no hay un concepto de puntos de aplicación de fuerzas al cuerpo, y este es un punto clave para determinar cómo rotará el cuerpo bajo su acción. La ecuación 5 es correcta. De hecho, es excelente para encontrar aceleración lineal. Nos falta la mitad de la batalla. Pero lo primero es lo primero ...

Cual es tu angulo

En el primer artículo, se ignoró la rotación, por lo que solo necesitábamos un vector de radio y su derivada para describir la configuración de nuestro cuerpo en 2D. Ahora agreguemos otro valor cinemático, orientación (denotado por la letra mayúscula omega - Ω), para trabajar con efectos de esquina. Para establecer Ω, debemos elegir el sistema de coordenadas relativo al sólido y el sistema de coordenadas del mundo del juego, y el valor de Ω será igual a la diferencia en ángulos entre ellos en radianes, como se muestra en la Figura 1.



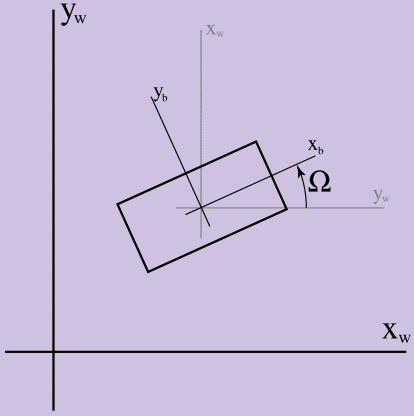Figura 1. Definición de Ω

En la figura, los ejes xw, yw son los ejes de coordenadas del mundo del juego, y xb, yb son los ejes de coordenadas del sólido. Ω es mayor que 0 si se cuenta en sentido antihorario. Aquí es importante aclarar por qué estudiamos la dinámica del mundo bidimensional antes de pasar al tridimensional: la orientación en 2D es una cantidad escalar (el ángulo entre sistemas de coordenadas en radianes), mientras que determinar la orientación en el mundo tridimensional es mucho más difícil.

A medida que el cuerpo gira, el valor de Ω cambia. Este cambio nos lleva a otra cinemática: la velocidad angular (denotada por la letra minúscula omega - ω). En contraste con la coordenada y la velocidad lineal del cuerpo, no denotamos la velocidad angular como sigue: Ω '. Sin embargo, a veces denotamos la derivada de la velocidad con respecto al tiempo, o la aceleración angular, como ω '(este es otro valor cinemático) o como α (alfa en minúscula). No me culpes: no se me ocurrieron todas estas designaciones; y en cada libro que leo hay ligeras discrepancias. Nuestra contraparte angular para la ecuación 1 es:

$$$$ display $$ {d ^ 2 Ω \ over {dt ^ 2}} = {dω \ over {dt}} = ω '= α $$ display $$

Ecuación 6

Como en la ecuación 1, diferenciamos ω en el tiempo para obtener α; y si integramos α a lo largo del tiempo, obtenemos ω, etc. Todo por analogía con el artículo anterior: conociendo la aceleración angular de α, podemos integrarlo dos veces para obtener una nueva orientación. Pero el punto clave aquí es conocer el valor de α.

Como puede imaginar, nuestro objetivo para este artículo es derivar un análogo angular para cada una de las ecuaciones lineales en la Tabla 1, y luego, teniendo en cuenta las ecuaciones lineales y angulares y la fuerza aplicada al objeto, podemos calcular su aceleración lineal ay la aceleración angular α. Finalmente, podemos integrar numéricamente estas aceleraciones para encontrar nuevas posiciones y orientaciones de nuestros cuerpos.

Para empezar, conectaremos cantidades lineales y angulares juntas. Y este es un truco bastante obvio en el que se usa la velocidad angular. Al calcular en dinámica, a menudo necesitamos encontrar la velocidad de un punto arbitrario en un objeto. Por ejemplo, cuando calculamos colisiones de sólidos, necesitamos conocer la velocidad de los puntos de colisión para comprender cuánto se golpean entre sí. Si nuestros cuerpos no giran, la velocidad de cada punto del cuerpo es la misma. Simplemente podemos controlar la velocidad del centro de masa del cuerpo, y eso será suficiente. Mientras que si nuestros cuerpos giran, cada punto de estos cuerpos puede tener una velocidad diferente. Obviamente, no podemos calcular la velocidad de un número infinito de puntos de nuestro cuerpo rígido, por lo tanto, necesitamos una solución diferente y mejor.

Uno de los métodos simples que se utilizan para encontrar la velocidad lineal de cualquier punto dentro de un objeto utiliza la velocidad angular del objeto. Considere el caso cuando el cuerpo gira solo alrededor de un punto fijo O, sin cambiar la coordenada del cuerpo. Es decir, el cuerpo gira, pero no se mueve. De la ecuación 7 se sigue cómo calcular la velocidad del punto B de un cuerpo giratorio:

$$$$ display $$ v ^ B = ωr ^ {OB} _⟂ $$ display $$

Ecuación 7

Necesitamos aclarar un par de puntos en la Ecuación 7, dediquemos un tiempo a esto. Primero, uso la indexación superior para mostrar qué parámetro pertenece a estos puntos, por lo que v ^ B es el vector de velocidad del punto B de nuestro cuerpo. Del mismo modo, r ^ OB denota un vector dibujado desde el centro de rotación de nuestro cuerpo O hasta el punto B. La divertida letra invertida T es el "operador perpendicular" que actúa sobre el vector (como el vector r en la ecuación 7) y lo gira 90 grados en sentido antihorario flechas En otras palabras, se construye un nuevo vector que es perpendicular al anterior. En un mundo bidimensional, un vector perpendicular a (x, y) es solo (-y, x). Puede verificar fácilmente mis palabras en una hoja de papel cuadriculado. Hablemos más sobre esto. La magnitud del vector perpendicular está determinada por la velocidad angular ω y establece la velocidad lineal v ^ B. En ruso, la ecuación 7 muestra que la velocidad de un punto de un cuerpo giratorio se calcula multiplicando el vector perpendicular dibujado desde el centro de rotación por la velocidad angular. ¿Cómo entiendo eso? Bueno, lo leí en el libro, pero es obvio que tal explicación no es suficiente, por lo que demostramos que esto es cierto.

Probemos la verdad de las conclusiones de la ecuación 7 en dos etapas. Primero, demostramos que el valor del vector de velocidad resultante es correcto; entonces, que su dirección es correcta. Para la primera parte de la prueba, considere la Figura 2.



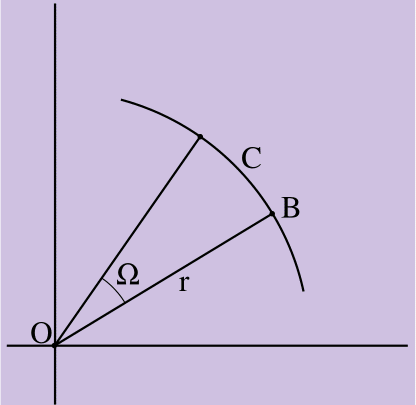Figura 2. C = Ωr

La Figura 2 muestra la rotación del punto B en un ángulo igual a Ω radianes a lo largo de la rotación de un cuerpo rígido con un vector de radio de longitud r dirigido desde el centro de rotación del cuerpo O al punto B. B pasó la longitud del arco C, donde C = Ωr de la definición de radianes. (Una medida en radianes de un ángulo es una medida de un arco delimitado por el radio de un círculo. La circunferencia de un círculo es C = 2πr porque la medida en radianes de un arco de un círculo es 2π [o 360 grados]).

La velocidad de un punto es un cambio en su coordenada en el tiempo. Por lo tanto, podemos encontrar la velocidad del punto B, en otras palabras, la magnitud del vector de velocidad, al diferenciar las ecuaciones de movimiento con respecto al tiempo. C = Ωr es la ecuación de movimiento.

$$

$${d (Ωr) \ over {dt}} = {dΩ \ over {dt}} r = ωr$$

El radio se saca del signo de diferenciación, porque es una constante (el punto B simplemente gira, sin movimiento lineal), y la derivada del tiempo Ω es ω de la ecuación 6. Por lo tanto, la magnitud del vector B es el vector de velocidad ωr.

Al considerar la Ecuación 7, notamos que la magnitud del vector de velocidad es correcta, ya que la perpendicular no afecta la longitud del vector y r ^ OB es un vector de radio dirigido de O a B. Fuh, estamos a medio camino.

Para verificar que la dirección del vector de velocidad en la ecuación 7 es correcta, comencemos por asegurarnos de que el vector de velocidad debe ser perpendicular al vector de radio. Esta suposición es comprensible intuitivamente, porque un punto que gira alrededor de otro punto dado solo puede moverse perpendicular al vector entre estos puntos. No puede acercarse al centro de rotación o alejarse de él, o este movimiento simplemente dejará de ser rotación. Podemos apoyar nuestra suposición con cálculos para vectores, pero estoy sujeto en un marco determinado para el volumen del artículo, por lo que asumiremos que nuestra suposición es correcta. (Si está ansioso por demostrarlo por su cuenta, diferencie el producto escalar de un vector de longitud fija por sí mismo).

Finalmente, debemos asegurarnos de que el vector esté marcado correctamente, porque la figura muestra dos vectores de igual longitud perpendiculares al radio: v y -v. Como el valor de Ω se mide en sentido antihorario, ω> 0 cuando el punto gira en sentido horario. Los puntos perpendiculares en el sentido de las agujas del reloj, al igual que el vector de radio. La Figura 3 muestra las conclusiones de la Ecuación 7:



Figura 3. Relación entre velocidad lineal y angular

Complemente la ecuación 7 para describir la rotación de los cuerpos móviles. Consideramos el movimiento de un cuerpo sólido como un simple movimiento del centro de rotación del cuerpo y una simple rotación del resto del cuerpo alrededor de este punto. Para aquellos que estén interesados, este es el teorema de Schal sobre la clasificación de los movimientos.

El teorema de Chall divide nuestro movimiento en dos componentes: lineal y angular. Deje que el centro de rotación del cuerpo O sea el único punto de movimiento, luego usamos ω para calcular la rotación alrededor del punto O, y esto nos da la forma general de la ecuación 7:

$$$$ display $$ v ^ B = v ^ O + ωr ^ {OB} _⟂ $$ display $$

Ecuación 9

La ecuación 9 dice que podemos calcular la velocidad de cualquier punto de un cuerpo en movimiento usando la velocidad lineal del centro de rotación del cuerpo y, además, la velocidad adquirida durante la rotación del cuerpo.

Motivo de nuestro impulso.

Ahora podemos escribir un análogo angular de la ecuación 2, la ecuación de fuerza. Comenzamos determinando el momento angular, L ^ AB de un punto B dado, alrededor de otro punto A:

$$

$${L} ^ {AB} = {\ vec r} ^ {AB} \ times {\ vec p} ^ B$$

Ecuación 10

El momento de impulso de un punto difiere del momento lineal de un punto en que la versión angular de la ecuación tiene en cuenta la posición del cuerpo en el espacio. De esto se deduce que el momento angular de un punto debe medirse para otro lugar en el mundo del juego, en contraste con el impulso lineal, que se determina para un punto dado (el producto de su masa y velocidad). Esto se muestra a través de la indexación superior en la ecuación 10. La notación L ^ AB dice que el momento angular se mide para el punto B desde el punto A (centro de rotación del cuerpo). Imagine una flecha apuntando desde el punto A al punto B. Esta flecha es un vector de radio entre dos puntos, significa r ^ AB. Entonces, el momento angular de un punto es un producto escalar de un vector de momento lineal y un vector de radio perpendicular a él. Esta operación se llama el "producto escalar con perpendicular", y es un análogo 2D para el producto vectorial 3D, pero lo discutiremos en otro momento.

Si representa gráficamente lo que sigue de la ecuación 10, en papel, como lo hice en la Figura 4, verá que determina la medida de cómo el momento lineal del punto B "gira" alrededor de A.



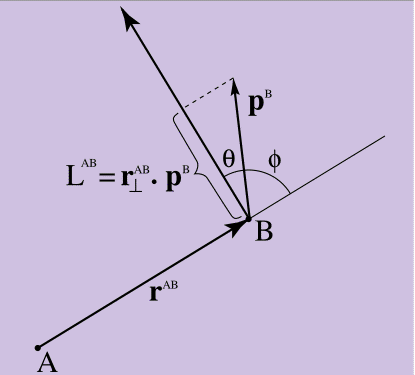Figura 4. Momento de impulso

Todo es correcto si el momento del punto B apunta directamente al punto A, ecuación 10 = 0 (ya que la perpendicular a r forma un ángulo recto con p, y el producto escalar será 0). Cuanto mayor sea el impulso B dirigido perpendicular a A, mayor será el impulso. Como se puede ver en la Figura 4, el producto escalar en la Ecuación 10 tiene como parámetro el coseno del ángulo θ encerrado entre la perpendicular r ^ AB a p ^ B. Si lo miras por otro lado, la magnitud del producto escalar viene dada por el seno del ángulo φ entre el original, no perpendicular r ^ AB y p ^ B (el seno es otra clave para desentrañar la conexión entre el vector y el producto escalar). La ecuación 10 da una medida de la cantidad de impulso del punto B "mira" en la "dirección de rotación" en relación con el punto A.

Además, como usamos la derivada del momento lineal para determinar la fuerza, usaremos la derivada del momento angular para determinar el gemelo angular de la fuerza: el momento de la fuerza (indicado por la letra minúscula tau - τ).

$$

$$τ ^ {AB} = {dL ^ {AB} \ over dt} = {d ({\ vec r} ^ {AB} \ times {\ vec p} ^ B) \ over dt} = \ vec r ^ { AB} \ veces ma ^ B = \ vec r ^ {AB} \ veces F ^ B$$

Ecuación 11

Para ahorrar espacio, hice un poco de trampa en la Ecuación 11, omitiendo un par de pasos difíciles que implicaban encontrar derivados. De lo anterior, se deduce que el momento de fuerza está asociado con la fuerza en un determinado punto a través de un producto escalar.

Finalmente, obtuvimos una ecuación dinámica que utiliza el punto de aplicación de la fuerza, que anteriormente se ignoraba en las ecuaciones de momento lineal. La ecuación 11 utiliza un producto escalar con una perpendicular como medida de la cantidad de fuerza aplicada al punto B que gira alrededor del punto A; Esta "fuerza de rotación" se llama el momento de la fuerza. La ecuación 11 le permite encontrar el valor numérico del momento de fuerza y, por lo tanto, el momento angular, si integramos el momento de fuerza, conociendo la fuerza aplicada y el punto de aplicación.

Sin embargo, todavía no hemos recibido la ecuación de la relación entre el momento de fuerza y ​​las magnitudes angulares de la cinemática que necesitamos para rotar el objeto alrededor de su eje, como la aceleración angular, la velocidad angular u orientación. Por lo tanto, no podemos avanzar antes de derivar algunas ecuaciones más.

El momento que todos hemos estado esperando

Antes de hacer una conexión entre la dinámica y la cinemática, necesitamos determinar el momento angular total, por analogía con cómo determinamos el momento lineal total en la Ecuación 4. No me he olvidado del equivalente angular para el centro de masa en la Ecuación 3; Lo veremos en la ecuación del momento angular total.

El momento angular total cerca del punto A se denota por L ^ AT y se determina por la ecuación 12:

$$

$$L ^ {AT} = {\ sum _ {i} {} {\ vec r ^ {Ai} \ times p ^ i}} = {\ sum _ {i} {\ vec r ^ {Ai} \ times m ^ iv ^ i}}$$

Ecuación 12

La ecuación 12 es la suma de todos los momentos angulares de todos los puntos del cuerpo, medidos en relación con el punto A. En el lado derecho, utilicé la definición de momento lineal para representar p ^ i como el producto de masa y velocidad (mv). Esto me será útil en el futuro para hacer de la Ecuación 12 algo con un carácter aplicado más pronunciado. La ecuación dice que para encontrar el momento angular total de nuestro objeto, es necesario sumar el momento angular de todos sus puntos. Para un cuerpo sólido que consta de caras (y no de puntos separados), es necesario calcular la integral, para una suma no discreta.

Afortunadamente, podemos simplificar nuestros cálculos al introducir una nueva cantidad llamada "momento de inercia", similar a cómo introdujimos el centro de masa para simplificar la ecuación de momento total. Recuerde que, gracias a la ecuación 7, podemos encontrar la velocidad de un punto a través de la velocidad angular. Si el punto A en la ecuación 12 es el centro de rotación de la ecuación 7, y el índice de suma i en la ecuación 12 es el punto B de la ecuación 7, entonces es posible convertir la ecuación 7 en la ecuación 12. Obtenemos:

$$

$$L^{AT} = \sum _{ i} {\vec r ^{Ai} \times m^i ω \vec r^{Ai}} = ω {\sum _{ i} {m^i \vec r^{Ai} \times \vec r ^{Ai}}} = ω \sum_{ i} {m^i (\vec r ^{Ai})^2} = ωI^A$$

Ecuación 13

Escribiré la ecuación 13 con más detalle, paso a paso. Primero, reemplazamos la ecuación 7 con 12 para obtener la suma en la ecuación 13. Este reemplazo nos permite describir el momento angular usando la velocidad angular. Luego, tomamos ω para la suma, porque es igual para todos los puntos del sólido (la velocidad angular se determina para todo el cuerpo, y no para cada punto por separado), y escribimos la masa con el índice i a la izquierda, para ver más claramente el radio del producto escalar -vectores para ellos mismos. Este producto escalar es igual al cuadrado de la longitud del radio vector (el producto escalar de cualquier vector en sí mismo = el cuadrado de su longitud. Recuerde que el operador perpendicular no cambia la longitud del vector). Finalmente, escribimos I ^ A para denotar el momento de inercia alrededor del punto A.

El momento de inercia para un sólido bidimensional es un número extremadamente bueno, porque los puntos que componen el cuerpo no pueden cambiar su masa o alejarse del centro de rotación. Como consecuencia de estas dos propiedades, la suma en la ecuación 13 es una constante para cada cuerpo, por lo que podemos calcularla. Hablando en ruso, I ^ A es la suma de las distancias al cuadrado desde el punto A a todos los demás puntos del cuerpo, y cada una de esas distancias se escala de acuerdo con la masa de cada punto. Al igual que para el centro de masa: si el cuerpo es más sólido que compuesto de puntos discretos, las sumas se convertirán en integrales. Y el momento de inercia seguirá siendo el mismo en magnitud y tendrá el mismo significado físico.

Determinar el momento de inercia cerca de un punto es detallado, pero piense en I ^ A como la medida de lo difícil que es girar el cuerpo alrededor del punto A. Por ejemplo, imagine un lápiz (lápiz plano). Si medimos el momento de inercia cerca del centro del lápiz, obtenemos un cierto valor igual a la suma de los cuadrados de las distancias escaladas de acuerdo con la masa de cada punto. Mientras que si medimos la inercia en la punta del mismo lápiz, obtenemos un valor mayor, porque cuanto más se eliminan los puntos con masa, mayor es el valor de los cuadrados de sus distancias. Aquí formularemos matemáticamente lo que es intuitivo para nosotros: rotar un lápiz alrededor de su centro es mucho más fácil (leerlo requiere menos esfuerzo) que rotarlo alrededor de uno de los extremos.

Finalmente, estamos listos para establecer una conexión entre las ecuaciones angulares de la dinámica y las ecuaciones angulares de la cinemática. Si diferenciamos la Ecuación 13, obtenemos el momento total de fuerza a la izquierda y el producto del momento de inercia y aceleración angular a la derecha (I ^ A es una constante, lo ponemos fuera del signo de diferenciación):

$$

$$τ^{AT} = {dL^{AT} \over dt} = {d( I^A ω) \over dt} = I^A ω = I^A α$$

Ecuación 14

Esta ecuación es el equivalente angular de la Ecuación 5; de hecho, es F = ma para dinámica angular. Esta es la ecuación de la conexión del momento total de fuerza y ​​la aceleración angular del cuerpo a través del momento escalar de inercia. Si conocemos el momento de fuerza ejercido sobre nuestro cuerpo, podemos encontrar su aceleración angular, y luego la velocidad angular y la orientación en el espacio a través de la integración, dividiendo el momento de fuerza por el momento de inercia.

Algoritmo de dinámica

Apenas nos ve a través de este torbellino de ecuaciones, pero todas ellas son su parte integral. Hemos derivado suficientes ecuaciones para obtener la magnífica dinámica de un mundo bidimensional con fuerzas arbitrarias y momentos de fuerzas que mueven y giran nuestros objetos. ¿Cómo usar estas ecuaciones? A continuación se muestra el algoritmo básico:

1. Encuentre el valor del centro de masa y el momento de inercia en el centro de masa.
2. Establezca las coordenadas iniciales del cuerpo, su orientación en el espacio, sus velocidades lineales y angulares.
3. Tenga en cuenta todas las fuerzas que actúan sobre el cuerpo y los puntos de su aplicación.
4. Encuentre la resultante de todas las fuerzas y divídala por la masa del cuerpo para encontrar la aceleración lineal del centro de masa (Ecuación 5).
5. , , , ( 11).
6. ( 14).
7. , , ( ).
8. , 3.

En el algoritmo anterior, solo hay dos pasos que no he explicado. Primero, ¿cómo calcular el momento de inercia en el Paso 1 para un objeto sólido? En segundo lugar, ¿cómo resolver el problema con las fuerzas del Paso 3? La respuesta a la primera pregunta se puede encontrar en un ejemplo de código simple, que dejaré en la aplicación al final de este artículo (integrará el objeto por su área). Muchos libros sobre dinámica contienen el momento de inercia calculado para las formas de objetos que se encuentran con frecuencia en la aplicación al final, por lo que no tiene que mostrarlos usted mismo cada vez.

La respuesta a la pregunta de cómo calcular las fuerzas del Paso 3 depende de la aplicación, pero daré algunas recomendaciones generales. En primer lugar, fuerzas como la gravedad, siempre dirigidas en una dirección (hacia abajo, en el caso de la gravedad), no crean un momento de fuerza, porque tiran de todos los puntos al mismo tiempo en la misma dirección, aunque Aplicamos estas fuerzas directamente al centro de masa. Se aplican fuerzas similares a la fuerza elástica en un determinado punto del objeto, crearán un momento de fuerza, por lo tanto, las consideramos en el caso general. Como vimos en el primer artículo, la fuerza de fricción es la misma fuerza dirigida en la dirección opuesta a la velocidad del cuerpo.

Puede hacer un modelo físico simple que demuestre la fuerza de fricción, y simplemente aplicar fuerza al centro de masa, o puede elegir qué partes del objeto aplicarán fuerzas de fricción, y hacer esto, lo que puede crear un momento de fuerza que actúa sobre el objeto. Las fuerzas que los cuerpos experimentan en colisiones son un poco más difíciles, y las conoceremos en el próximo artículo. Las fuerzas como el empuje de un motor de cohete deben considerarse fuerzas con un punto de aplicación (en este caso, si uno de los motores falla, comenzará a girar alrededor de su eje hasta que ajuste el volante para equilibrar el momento de la fuerza). Si quieres algo similar a los rayos gravitacionales de un OVNI, entonces esta fuerza debe calcularse como la fuerza de gravedad y no crear un momento de fuerza, o debe aplicarse a un punto específico del objeto,¿Y girará en torno a este punto mientras se levanta? La elección es tuya. El punto clave es no tener miedo de experimentar con diferentes fuerzas calculadas de diferentes maneras, porque ahora que tiene un simulador gráfico bidimensional real, ¡pruebe diferentes tipos de fuerzas!

Dejé todo el código y los enlaces que necesita en mi sitio web porque no queda más espacio. En mi aplicación simple, implementé el algoritmo de la dinámica de un mundo bidimensional, y también agregué objetos sujetos por un resorte; giran alrededor de su eje, y a veces incluso chocan con paredes, giran. Pero hablaré de esto en otra ocasión. Siga el enlace para obtener más literatura y una aplicación simple para Windows 32 y Macintosh.

Muy raramente, Chris Hecker experimenta el efecto del momento de inercia, pero generalmente pasa con bastante rapidez. Las fuerzas se pueden aplicar a checker@bix.com.

Notas del traductor: aquí se presenta un juego de palabras, se reproduce el tema del artículo y su contenido.

PD Feedback es bienvenido. Sus comentarios pueden mejorar la calidad del trabajo. Gracias

PPS El autor de la traducción expresa un agradecimiento especial a los usuarios de berez y Vasily Tereshkov por editar la traducción. Gracias