Matrices de antenas adaptativas: ¿cómo funciona? (Básico)

Buen dia

Los últimos años me he dedicado a la investigación y creación de varios algoritmos para el procesamiento espacial de señales en matrices de antenas adaptativas, y continúo haciendo esto como parte de mi trabajo en este momento. Aquí me gustaría compartir el conocimiento y las fichas que descubrí. Espero que sea útil para las personas que comienzan a estudiar esta área de procesamiento de señales o simplemente están interesadas.

¿Qué es un conjunto de antenas adaptativas?

Un conjunto de antenas es un conjunto de elementos de antena, dispuestos de alguna manera en el espacio. Para simplificar la estructura del conjunto de antenas adaptativas, que consideraremos, se puede representar de la siguiente forma:


Las matrices de antenas adaptativas a menudo se denominan "antenas inteligentes" (antenas inteligentes ). El conjunto de antenas "inteligentes" está formado por la unidad de procesamiento de señal espacial y los algoritmos implementados en ella. Estos algoritmos analizan la señal recibida y forman un conjunto de pesos.$$ $ en línea $ w_1 ... w_N $ en línea $ que determinan la amplitud y la fase inicial de la señal para cada uno de los elementos. La distribución de amplitud-fase dada determina el patrón de directividad de toda la red como un todo. La capacidad de sintetizar el patrón de radiación de la forma requerida y cambiarlo durante el procesamiento de la señal es una de las características principales de los conjuntos de antenas adaptativas, lo que permite resolver una amplia gama de problemas . Pero lo primero es lo primero.

¿Cómo se forma el patrón de radiación?

Un patrón de radiación caracteriza el poder de una señal radiada en una determinada dirección. Por simplicidad, ponemos los elementos de la red isotrópicos, es decir Para cada uno de ellos, la potencia de la señal emitida no depende de la dirección. La amplificación o atenuación de la potencia radiada por el conjunto en una determinada dirección se obtiene debido a la interferencia de las ondas electromagnéticas emitidas por varios elementos del conjunto de antenas. Un patrón de interferencia estable para EMW solo es posible si son coherentes , es decir La diferencia de fase de las señales no debe cambiar con el tiempo. En el caso ideal, cada uno de los elementos del conjunto de antenas debería emitir una señal armónica a la misma frecuencia portadora$$ $ en línea $ f_ {0} $ en línea $ . Sin embargo, en la práctica, es necesario trabajar con señales de banda estrecha que tengan un espectro de ancho finito$$ $ en línea $ \ Delta f << f_ {0} $ en línea $ .
Deje que todos los elementos AR emitan la misma señal con amplitud compleja$$ $ en línea $ x_n (t) = u (t) $ en línea $ . Luego, en el receptor remoto , la señal recibida desde el enésimo elemento se puede representar de forma analítica :

$$$$ display $$ a_n (t) = u (t- \ tau_n) e ^ {i2 \ pi f_0 (t- \ tau_n)} $$ display $$

donde$$ $ en línea $ \ tau_n $ en línea $ - retraso en la propagación de la señal desde el elemento de antena hasta el punto de recepción.
Dicha señal es "cuasi armónica", y para satisfacer la condición de coherencia, es necesario que el retraso máximo en la propagación de ondas electromagnéticas entre dos elementos sea mucho menor que el tiempo característico del cambio de envolvente de la señal.$$ $ en línea $ T $ en línea $ es decir$$ $ en línea $ u (t- \ tau_n) ≈ u (t- \ tau_m) $ en línea $ . Por lo tanto, la condición para la coherencia de una señal de banda estrecha se puede escribir de la siguiente manera:

$$$$ display $$ T≈ \ frac {1} {\ Delta f} >> \ frac {D_ {max}} {c} = max (\ tau_k- \ tau_m) $$ display $$

donde$$ $ en línea $ D_ {max} $ en línea $ - la distancia máxima entre los elementos del AR , y$$ $ en línea $ con $ en línea $ Es la velocidad de la luz.

Al recibir una señal, la suma coherente se realiza digitalmente en la unidad de procesamiento espacial. En este caso, el valor complejo de la señal digital en la salida de este bloque está determinado por la expresión:

$$$$ display $$ y = \ sum_ {n = 1} ^ Nw_n ^ * x_n $$ display $$

Es más conveniente presentar la última expresión en forma de un producto escalar de vectores complejos N-dimensionales en forma de matriz:

$$$$ display $$ y = (\ textbf {w}, \ textbf {x}) = \ textbf {w} ^ H \ textbf {x} $$ display $$

donde w y x son vectores de columna, y$$ $ en línea $ (.) ^ H $ en línea $ - operación de emparejamiento hermitiano .

La representación vectorial de señales es uno de los elementos básicos cuando se trabaja con matrices de antenas, porque a menudo evita cálculos matemáticos engorrosos. Además, la identificación de una señal recibida en un determinado momento con un vector a menudo nos permite abstraernos de un sistema físico real y comprender qué sucede exactamente desde el punto de vista de la geometría.

Para calcular el patrón de directividad del conjunto de antenas, es necesario "ejecutar" mental y consistentemente un conjunto de ondas planas desde todas las direcciones posibles. En este caso, los valores de los elementos del vector x se pueden representar de la siguiente manera:

$$$$ display $$ x_n = s_n = \ exp \ {- i (\ textbf {k} (\ phi, \ theta), \ textbf {r} _n) \} $$ display $$

donde k es el vector de onda$$ $ en línea $ \ phi $ en línea $ y$$ $ en línea $ \ theta $ en línea $ - ángulo azimutal y ángulo de elevación que caracterizan la dirección de llegada de una onda plana,$$ $ en línea $ \ textbf {r} _n $ en línea $ - coordenada del elemento de antena,$$ $ en línea $ s_n $ en línea $ - un elemento del vector de fases s de una onda plana con el vector de ondas k (en la literatura inglesa, el vector de fases se denomina vector de dirección). La dependencia del cuadrado de la amplitud de y en$$ $ en línea $ \ phi $ en línea $ y$$ $ en línea $ \ theta $ en línea $ determina el patrón de directividad del conjunto de antenas en recepción para un vector dado de coeficientes de peso w .

Características del conjunto de antenas

Es conveniente estudiar las propiedades generales del diagrama de radiación del conjunto de antenas en un conjunto de antenas equidistantes lineales en un plano horizontal (es decir, el patrón del haz depende solo del ángulo azimutal$$ $ en línea $ \ phi $ en línea $ ) Es conveniente desde dos puntos de vista: cálculos analíticos y presentación visual.

Calculamos el DN para un vector de peso unitario ($$ $ en línea $ w_n = 1, n = 1 ... N $ en línea $ ), siguiendo el enfoque descrito anteriormente .


Como resultado, obtenemos:

$$$$ display $$ F (\ phi) = | y | ^ 2 = \ frac {\ sin ^ 2 (\ pi \ frac {Nd} {\ lambda} \ sin \ phi)} {\ sin ^ 2 (\ pi \ frac {d} {\ lambda} \ sin \ phi)} $$ display $$

Frecuencia de patrón de radiación

El patrón de radiación resultante del conjunto de antenas es una función periódica del seno del ángulo. Esto significa que para ciertos valores de la relación d / λ , tiene máximos de difracción (adicionales).
Patrón de antena no normalizado para N = 5
Diagrama de radiación normalizado del conjunto de antenas para N = 5 en el sistema de coordenadas polares

La posición de los "difraccionistas" se puede ver directamente desde la fórmula para NAM. Sin embargo, trataremos de comprender de dónde provienen física y geométricamente (en el espacio N-dimensional).

Los elementos del vector s en fases son exponentes complejos$$ $ en línea $ e ^ {i \ Psi n} $ en línea $ cuyos valores están determinados por el valor del ángulo generalizado$$ $ en línea $ \ Psi = 2 \ pi \ frac {d} {\ lambda} \ sin \ phi $ en línea $ . Si hay dos ángulos generalizados correspondientes a diferentes direcciones de llegada de una onda plana, para lo cual$$ $ en línea $ \ Psi_1 = \ Psi_2 + 2 \ pi m $ en línea $ , entonces esto significa dos cosas:

• Físicamente: los frentes de ondas planas que provienen de estas direcciones inducen distribuciones idénticas de amplitud-fase de ondas electromagnéticas en los elementos del conjunto de antenas.
• Geométricamente: los vectores de fase para estas dos direcciones coinciden.

Las direcciones de llegada de ondas conectadas de manera similar son equivalentes desde el punto de vista de la matriz de antenas y no son distinguibles entre sí.

¿Cómo determinar la región de ángulos en la que siempre se encuentra un máximo máximo de MD ? Haremos esto cerca del azimut cero por las siguientes razones: el cambio de fase entre dos elementos adyacentes debe estar en el intervalo de$$ $ en línea $ - \ pi $ en línea $ antes$$ $ en línea $ \ pi $ en línea $ .

$$$$ display $$ - \ pi <2 \ pi \ frac {d} {\ lambda} \ sin \ phi <\ pi $$ display $$

Al resolver esta desigualdad, obtenemos la condición en la región de unicidad en un vecindario de cero:

$$$$ display $$ | \ sin \ phi | <\ frac {\ lambda} {2d} $$ display $$

Se puede ver que el tamaño de la región de unicidad en ángulo depende de la relación d / λ . Si d = 0.5 λ , entonces cada dirección de llegada de la señal es "individual", y la región de unicidad cubre el rango completo de ángulos. Si d = 2.0 λ , entonces las direcciones 0, ± 30, ± 90 son equivalentes. Los lóbulos de difracción aparecen en el patrón de radiación.

Típicamente, los lóbulos de difracción tienden a suprimirse usando elementos de antena direccionales. En este caso, el patrón de radiación completo del conjunto de antenas es el producto del patrón de un elemento y el conjunto de elementos isotrópicos. Los parámetros DN de un elemento generalmente se seleccionan en función de la condición en la región de unicidad del conjunto de antenas.

El ancho del lóbulo principal.

La fórmula de ingeniería para estimar el ancho del lóbulo principal del sistema de antena es ampliamente conocida :$$ $ en línea $ \ Delta \ phi ≈ \ frac {\ lambda} {D} $ en línea $ donde D es el tamaño característico de la antena. La fórmula se usa para varios tipos de antenas, incluidas las SLR. Mostramos que también es válido para matrices de antenas.

Determinamos el ancho del lóbulo principal por los primeros ceros del MD en la vecindad del máximo principal. Numerador de expresión para$$ $ en línea $ F (\ phi) $ en línea $ desaparece en$$ $ en línea $ \ sin \ phi = m \ frac {\ lambda} {dN} $ en línea $ . Los primeros ceros corresponden a m = ± 1. Asumiendo$$ $ en línea $ \ frac {\ lambda} {dN} << 1 $ en línea $ tenemos$$ $ en línea $ \ Delta \ phi = 2 \ frac {\ lambda} {dN} $ en línea $ .

Típicamente, el ancho de haz de directividad AR está determinado por el nivel de potencia media (-3 dB). En este caso, use la expresión:

$$$$ display $$ \ Delta \ phi≈0.88 \ frac {\ lambda} {dN} $$ display $$

El ancho del lóbulo principal se puede controlar estableciendo diferentes valores de las amplitudes para los coeficientes de peso del conjunto de antenas. Considere tres distribuciones:

• Distribución de amplitud uniforme (pesos 1):$$ $ en línea $ w_n = 1 $ en línea $ .
• Valores de amplitud que caen a los bordes de la red (pesos 2):$$ $ en línea $ w_n = 0.5 + 0.3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ en línea $
• Valores de amplitud que aumentan hasta los bordes de la rejilla (pesos 3):$$ $ en línea $ w_n = 0.5-0.3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ en línea $

La figura muestra los patrones de radiación normalizados resultantes en una escala logarítmica:
Las siguientes tendencias se pueden rastrear desde la figura: la distribución de las amplitudes de los coeficientes de peso que disminuyen hacia los bordes de la red conduce a una ampliación del lóbulo principal del MD, pero a una disminución en el nivel de los lóbulos laterales. Las amplitudes que aumentan hacia los bordes del conjunto de antenas, por el contrario, conducen a un estrechamiento del lóbulo principal y un aumento en el nivel de los lados. Es conveniente considerar limitar los casos aquí:

1. Las amplitudes de los coeficientes de ponderación de todos los elementos, excepto los extremos, son iguales a cero. Los pesos para elementos extremos son iguales a la unidad. En este caso, la red se convierte en equivalente a un AR de dos elementos con un período de D = (N-1) d . No es difícil estimar de acuerdo con la fórmula anterior el ancho del pétalo principal. En este caso, los laterales se convertirán en máximos de difracción y se alinearán con el máximo principal.
2. El peso del elemento central es igual a uno, y el resto a cero. En este caso, esencialmente tenemos una antena con un patrón de radiación isotrópica.

La dirección del máximo principal

Entonces, vimos cómo puede ajustar el ancho del lóbulo principal del AP AR . Ahora veamos cómo dirigir la dirección. Recuerde la expresión del vector para la señal recibida. Supongamos que queremos que el patrón de radiación máxima mire en cierta dirección$$ $ en línea $ \ phi_0 $ en línea $ . Esto significa que la potencia máxima debe tomarse desde esta dirección. El vector de fases corresponde a esta dirección.$$ $ en línea $ \ textbf {s} (\ phi_0) $ en línea $ en el espacio vectorial N- dimensional, y la potencia recibida se define como el cuadrado del producto escalar de este vector en fase por el vector de coeficientes de peso w . El producto escalar de dos vectores es máximo cuando son colineales , es decir.$$ $ en línea $ \ textbf {w} = \ beta \ textbf {s} (\ phi_0) $ en línea $ , donde β es algún factor de normalización. Por lo tanto, si elegimos un vector de peso igual al vector de fase para la dirección deseada, giraremos el patrón de radiación máxima.

Considere los siguientes pesos como ejemplo:$$ $ en línea $ \ textbf {w} = \ textbf {s} (10 °) $ en línea $

$$$$ display $$ w_n = \ exp \ {i2 \ pi \ frac {d} {\ lambda} (n-1) \ sin (10 \ pi / 180) \} $$ display $$

Como resultado, obtenemos un patrón de radiación con el máximo principal en la dirección de 10 °.

Ahora aplicamos los mismos pesos, pero no para la recepción de la señal, sino para la transmisión. Aquí vale la pena considerar que cuando se transmite una señal, la dirección del vector de onda se invierte. Esto significa que los elementos del vector de fase para recepción y transmisión difieren en el signo en el exponente, es decir. interconectados por conjugación compleja. Como resultado, obtenemos el máximo del patrón de radiación en la dirección de -10 °, que no coincide con el máximo de la señal de recepción en los mismos coeficientes de peso. Para corregir la situación, es necesario aplicar conjugación compleja también a los coeficientes de peso.

La característica descrita de la formación de los haces para recepción y transmisión siempre debe tenerse en cuenta al trabajar con conjuntos de antenas.

Juguemos con el patrón de radiación

Pocos máximos

Planteamos el problema para formar dos máximos principales del patrón de radiación en la dirección: -5 ° y 10 °. Para hacer esto, elegimos la suma ponderada de los vectores de fase para las direcciones correspondientes como el vector de peso.

$$$$ display $$ \ textbf {w} = \ beta \ textbf {s} (10 °) + (1- \ beta) \ textbf {s} (- 5 °) $$ display $$

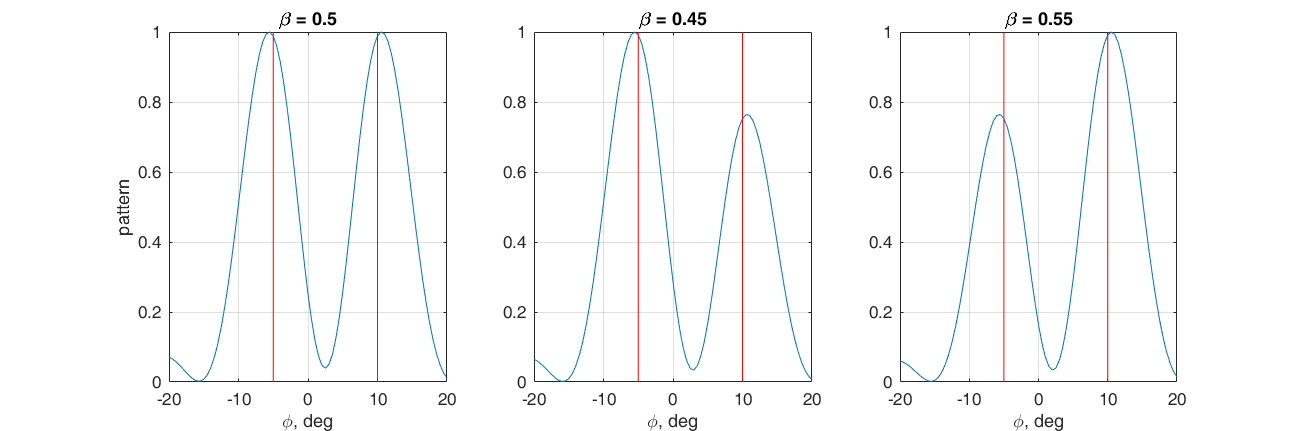
Al ajustar el coeficiente β , se puede ajustar la relación entre los lóbulos principales. Aquí nuevamente, es conveniente ver lo que está sucediendo en el espacio vectorial. Si β es mayor que 0.5, entonces el vector de pesos se encuentra más cerca de s (10 °), de lo contrario a s (-5 °). Cuanto más cerca esté el vector de peso de uno de los fasores, mayor será el producto escalar correspondiente y, por lo tanto, la magnitud del máximo correspondiente del ND .

Sin embargo, vale la pena considerar que ambos pétalos principales tienen un ancho finito, y si queremos sintonizar en dos direcciones cercanas, entonces estos pétalos se fusionarán en uno, orientado a alguna dirección intermedia.

Un máximo y cero

Ahora intentemos ajustar el patrón de radiación máxima a la dirección$$ $ en línea $ \ phi_1 = 10 ° $ en línea $ y simultáneamente suprimir la señal proveniente de la dirección$$ $ en línea $ \ phi_2 = -5 ° $ en línea $ . Para esto, es necesario establecer el cero para el ángulo correspondiente. Puede hacer esto de la siguiente manera:

$$$$ display $$ \ textbf {w} = \ textbf {s} _1- \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {N} \ textbf {s} _2 $$ display $$

donde$$ $ en línea $ \ textbf {s} _1 = \ textbf {s} (10 °) $ en línea $ y$$ $ en línea $ \ textbf {s} _2 = \ textbf {s} (- 5 °) $ en línea $ .

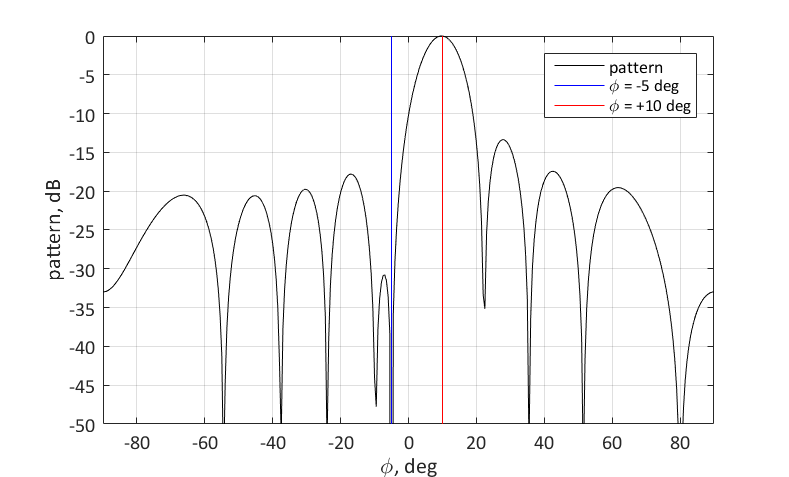
El significado geométrico de la elección del vector de peso es el siguiente. Queremos que este vector w tenga una proyección máxima en$$ $ en línea $ \ textbf {s} _1 $ en línea $ y era ortogonal al vector$$ $ en línea $ \ textbf {s} _2 $ en línea $ . Vector$$ $ en línea $ \ textbf {s} _1 $ en línea $ se puede representar como dos términos: vector colineal$$ $ en línea $ \ textbf {s} _2 $ en línea $ y vector ortogonal$$ $ en línea $ \ textbf {s} _2 $ en línea $ . Para satisfacer el enunciado del problema, es necesario elegir el segundo componente como el vector de coeficientes de peso w . El componente colineal se puede calcular diseñando un vector$$ $ en línea $ \ textbf {s} _1 $ en línea $ al vector normalizado$$ $ en línea $ \ frac {\ textbf {s} _2} {\ sqrt {N}} $ en línea $ utilizando un producto escalar.

$$$$ display $$ \ textbf {s} _ {1 ||} = \ frac {\ textbf {s} _2} {\ sqrt {N}} \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {\ sqrt {N}} $$ display $$

En consecuencia, restando del vector de fase inicial$$ $ en línea $ \ textbf {s} _1 $ en línea $ su componente colineal, obtenemos el vector de peso deseado.

Algunas notas adicionales

1. En todas partes arriba, omití la cuestión de normalizar el vector de peso, es decir su longitud Por lo tanto, la normalización del vector de peso no afecta las características del patrón de radiación del conjunto de antenas: la dirección de la máxima principal, el ancho del lóbulo principal, etc. También se puede demostrar que esta normalización no afecta la SNR a la salida del bloque de procesamiento espacial. En este sentido, cuando considero algoritmos de procesamiento de señales espaciales, generalmente acepto una normalización unitaria del vector de peso, es decir$$ $ en línea $ \ textbf {w} ^ H \ textbf {w} = 1 $ en línea $
2. Las posibilidades para la formación del fondo de la matriz de antenas están determinadas por el número de elementos N. Cuantos más elementos, mayores son las posibilidades. Cuantos más grados de libertad en la implementación del procesamiento de peso espacial, más opciones de cómo "torcer" el vector de peso en el espacio N-dimensional.
3. Cuando se recibe el patrón del haz de la antena , el conjunto de antenas no existe físicamente, y todo esto existe solo en la "imaginación" de la unidad informática que procesa la señal. Esto significa que, al mismo tiempo, es posible sintetizar varios MD y procesar de forma independiente las señales que llegan desde diferentes direcciones. En el caso de la transmisión, todo es algo más complicado, pero también es posible sintetizar varios MD para transmitir varios flujos de datos. Esta tecnología en sistemas de comunicación se llama MIMO .
4. Usando el código de matlab proporcionado, puedes jugar con NAM tú mismo
   
   Código

   % antenna array settings N = 10; % number of elements d = 0.5; % period of antenna array wLength = 1; % wavelength mode = 'receiver'; % receiver or transmitter % weights of antenna array w = ones(N,1); % w = 0.5 + 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = 0.5 - 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+10/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+3/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-3/180*pi)*(0:N-1)).'; % s1 = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % s2 = exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % w = s1 - (1/N)*s2*s2'*s1; % w = s1; % normalize weights w = w./sqrt(sum(abs(w).^2)); % set of angle values to calculate pattern angGrid_deg = (-90:0.5:90); % convert degree to radian angGrid = angGrid_deg * pi / 180; % calculate set of steerage vectors for angle grid switch (mode) case 'receiver' s = exp(2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); case 'transmitter' s = exp(-2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); end % calculate pattern y = (abs(w'*s)).^2; %linear scale plot(angGrid_deg,y/max(y)); grid on; xlim([-90 90]); % log scale % plot(angGrid_deg,10*log10(y/max(y))); % grid on; % xlim([-90 90]); 

   
   

¿Qué tareas se pueden resolver con la ayuda de un conjunto de antenas adaptativas?

Gracias por su atencion