Hola amigos El curso
Algorithms for Developers comienza mañana, y todavía tenemos una traducción inédita. En realidad corregimos y compartimos material con usted. Vamos
La Transformada rápida de Fourier (FFT) es uno de los algoritmos de procesamiento de señales y análisis de datos más importantes. Lo usé durante años sin conocimientos formales en informática. Pero esta semana se me ocurrió que nunca me pregunté cómo la FFT calcula la transformada discreta de Fourier tan rápido. Me sacudí el polvo de un viejo libro sobre algoritmos, lo abrí y leí con placer sobre el truco computacional engañosamente simple que J.V. Cooley y John Tukey describieron en su clásico
trabajo de 1965 sobre este tema.
El objetivo de esta publicación es sumergirse en el algoritmo Cooley-Tukey FFT, explicando las simetrías que lo conducen, y mostrar algunas implementaciones simples de Python que aplican la teoría en la práctica. Espero que este estudio brinde a los especialistas en análisis de datos, como yo mismo, una imagen más completa de lo que está sucediendo bajo el capó de los algoritmos que utilizamos.
Transformada discreta de FourierFFT es rápido
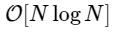
un algoritmo para calcular la transformada discreta de Fourier (DFT), que se calcula directamente para
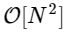
. El DFT, como la versión continua más familiar de la transformada de Fourier, tiene una forma directa e inversa, que se definen de la siguiente manera:
Transformada discreta directa de Fourier (DFT):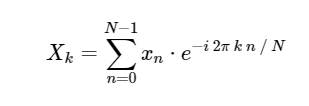
Transformada discreta inversa de Fourier (ODPF):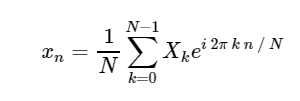
La conversión de
xn → Xk es una traducción del espacio de configuración al espacio de frecuencia y puede ser muy útil tanto para estudiar el espectro de potencia de la señal como para convertir ciertas tareas para un cálculo más eficiente. Puede encontrar algunos ejemplos de esto en acción en el
capítulo 10 de nuestro futuro libro sobre astronomía y estadísticas, donde también puede encontrar imágenes y el código fuente de Python. Para ver un ejemplo del uso de FFT para simplificar la integración de ecuaciones diferenciales complicadas, vea mi publicación
"Resolviendo la ecuación de Schrödinger en Python" .
Debido a la importancia de FFT (en adelante, se puede usar la FFT equivalente - Transformada rápida de Fourier) en muchas áreas de Python contiene muchas herramientas estándar y shells para calcularla. Tanto NumPy como SciPy tienen shells de la biblioteca FFTPACK extremadamente bien probada, que se encuentran en los
scipy.fftpack numpy.fft y
scipy.fftpack respectivamente. El FFT más rápido que conozco está en el paquete
FFTW , que también está disponible en Python a través del paquete
PyFFTW .
Por el momento, sin embargo, dejemos de lado estas implementaciones y preguntémonos cómo podemos calcular FFT en Python desde cero.
Cálculo discreto de la transformación de FourierPara simplificar, solo trataremos con la conversión directa, ya que la transformación inversa se puede implementar de una manera muy similar. Al observar la expresión anterior del DFT, vemos que esto no es más que una operación lineal directa: multiplicar la matriz por un vector
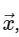
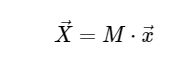
con matriz M dada
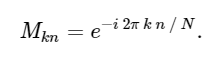
Con esto en mente, podemos calcular el DFT usando una simple matriz de multiplicación de la siguiente manera:
En [1]:
import numpy as np def DFT_slow(x): """Compute the discrete Fourier Transform of the 1D array x""" x = np.asarray(x, dtype=float) N = x.shape[0] n = np.arange(N) k = n.reshape((N, 1)) M = np.exp(-2j * np.pi * k * n / N) return np.dot(M, x)
Podemos verificar el resultado comparándolo con la función FFT incorporada en numpy:
En [2]:
x = np.random.random(1024) np.allclose(DFT_slow(x), np.fft.fft(x))
0ut [2]:
TrueSolo para confirmar la lentitud de nuestro algoritmo, podemos comparar el tiempo de ejecución de estos dos enfoques:
En [3]:
%timeit DFT_slow(x) %timeit np.fft.fft(x)
10 loops, best of 3: 75.4 ms per loop 10000 loops, best of 3: 25.5 µs per loop
Somos más de 1000 veces más lentos, lo que es de esperar para una implementación tan simplificada. Pero esto no es lo peor. Para un vector de entrada de longitud N, el algoritmo FFT se escala como
mientras que nuestro algoritmo lento escala como
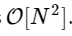
. Esto significa que para
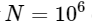
elementos, esperamos que la FFT se complete en aproximadamente 50 ms, ¡mientras que nuestro algoritmo lento tomará aproximadamente 20 horas!
Entonces, ¿cómo logra la FFT tal aceleración? La respuesta es usar simetría.
Simetrías en la transformada discreta de FourierUna de las herramientas más importantes en la creación de algoritmos es el uso de simetrías de tareas. Si puede demostrar analíticamente que una parte del problema está simplemente relacionada con la otra, puede calcular el resultado secundario solo una vez y ahorrar este costo computacional. Cooley y Tukey utilizaron exactamente este enfoque para obtener FFT.
Comenzamos con la cuestión del significado.
. De nuestra expresión anterior:
donde usamos la identidad exp [2π in] = 1, que se cumple para cualquier número entero n.
La última línea muestra bien la propiedad de simetría del DFT:
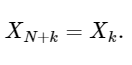
Una simple extensión
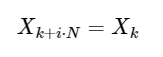
para cualquier número entero i. Como veremos a continuación, esta simetría se puede usar para calcular el DFT mucho más rápido.
DFT en FFT: usando simetríaCooley y Tukey mostraron que los cálculos de FFT se pueden dividir en dos partes más pequeñas. De la definición de DFT tenemos:
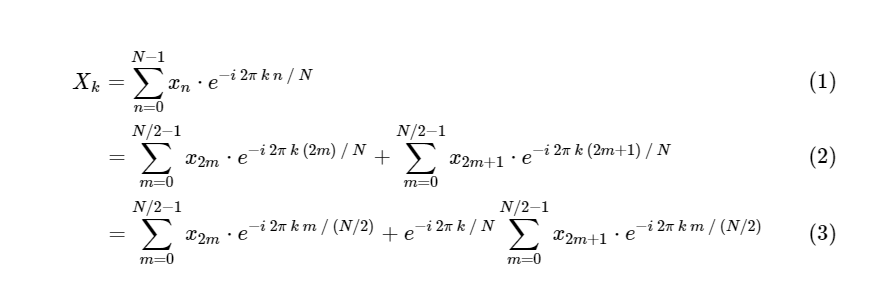
Dividimos una transformada discreta de Fourier en dos términos, que en sí mismos son muy similares a las transformadas discretas de Fourier más pequeñas, una a valores con un número impar y otra a valores con un número par. Sin embargo, hasta ahora no hemos guardado ningún ciclo computacional. Cada término consta de (N / 2) ∗ N cálculos, total
.
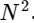
El truco es usar simetría en cada una de estas condiciones. Dado que el rango de k es 0≤k <N, y el rango de n es 0≤n <M≡N / 2, vemos por las propiedades de simetría anteriores que necesitamos realizar solo la mitad de los cálculos para cada subtarea. Nuestro cálculo
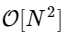
se ha convertido
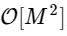
donde M es dos veces menos que N.
Pero no hay razón para detenerse en esto: siempre que nuestras transformadas de Fourier más pequeñas tengan una M uniforme, podemos volver a aplicar este enfoque de dividir y conquistar, reduciendo a la mitad el costo computacional, hasta que nuestras matrices sean lo suficientemente pequeñas como para que la estrategia ya no se beneficie. En el límite asintótico, este enfoque recursivo se escala como O [NlogN].
Este algoritmo recursivo se puede implementar muy rápidamente en Python, a partir de nuestro código DFT lento, cuando el tamaño de la subtarea se vuelve bastante pequeño:
En [4]:
def FFT(x): """A recursive implementation of the 1D Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if N % 2 > 0: raise ValueError("size of x must be a power of 2") elif N <= 32:
Aquí haremos una comprobación rápida de que nuestro algoritmo da el resultado correcto:
En [5]:
x = np.random.random(1024) np.allclose(FFT(x), np.fft.fft(x))
Fuera [5]:
TrueCompare este algoritmo con nuestra versión lenta:
-En [6]:
%timeit DFT_slow(x) %timeit FFT(x) %timeit np.fft.fft(x)
10 loops, best of 3: 77.6 ms per loop 100 loops, best of 3: 4.07 ms per loop 10000 loops, best of 3: 24.7 µs per loop
¡Nuestro cálculo es más rápido que la versión directa! Además, nuestro algoritmo recursivo es asintóticamente
: implementamos la rápida transformación de Fourier.
Tenga en cuenta que todavía no estamos cerca de la velocidad del algoritmo FFT incorporado numpy, y esto debería esperarse. El algoritmo FFTPACK detrás de
fft numpy es una implementación de Fortran que ha recibido años de refinamiento y optimización. Además, nuestra solución NumPy incluye tanto la recursión de la pila de Python como la asignación de muchas matrices temporales, lo que aumenta el tiempo de cálculo.
Una buena estrategia para acelerar el código cuando se trabaja con Python / NumPy es vectorizar los cálculos repetidos siempre que sea posible. Podemos hacer esto: en el proceso, eliminemos nuestras llamadas a funciones recursivas, lo que hará que nuestra Python FFT sea aún más eficiente.
Versión Numpy VectorizadaTenga en cuenta que en la implementación recursiva anterior de FFT, en el nivel más bajo de recursión, realizamos
N / 32 productos de matriz-vector idénticos. La efectividad de nuestro algoritmo ganará si calculamos simultáneamente estos productos matriz-vector como un solo producto matriz-matriz. En cada nivel de recursión posterior, también realizamos operaciones repetitivas que se pueden vectorizar. NumPy hace un excelente trabajo en dicha operación, y podemos usar este hecho para crear esta versión vectorizada de la rápida transformación de Fourier:
En [7]:
def FFT_vectorized(x): """A vectorized, non-recursive version of the Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if np.log2(N) % 1 > 0: raise ValueError("size of x must be a power of 2")
Aunque el algoritmo es ligeramente más opaco, es simplemente una reorganización de las operaciones utilizadas en la versión recursiva, con una excepción: usamos simetría en el cálculo de los coeficientes y construimos solo la mitad de la matriz. Nuevamente, confirmamos que nuestra función da el resultado correcto:
En [8]:
x = np.random.random(1024) np.allclose(FFT_vectorized(x), np.fft.fft(x))
Fuera [8]:
TrueA medida que nuestros algoritmos se vuelven mucho más eficientes, podemos usar una matriz más grande para comparar el tiempo, dejando
DFT_slow :
En [9]:
x = np.random.random(1024 * 16) %timeit FFT(x) %timeit FFT_vectorized(x) %timeit np.fft.fft(x)
10 loops, best of 3: 72.8 ms per loop 100 loops, best of 3: 4.11 ms per loop 1000 loops, best of 3: 505 µs per loop
¡Hemos mejorado nuestra implementación en un orden de magnitud! Ahora estamos a unas 10 veces del punto de referencia FFTPACK, usando solo un par de docenas de líneas de Python + NumPy puro. Aunque esto todavía no es computacionalmente consistente, en términos de legibilidad, la versión de Python es muy superior al código fuente FFTPACK, que puede ver
aquí .
Entonces, ¿cómo logra FFTPACK esta última aceleración? Bueno, básicamente, es solo una cuestión de contabilidad detallada. FFTPACK pasa mucho tiempo reutilizando cualquier cálculo intermedio que pueda reutilizarse. Nuestra versión irregular todavía incluye un exceso de asignación de memoria y copia; En un lenguaje de bajo nivel como Fortran, es más fácil controlar y minimizar el uso de memoria. Además, el algoritmo Cooley-Tukey se puede extender para usar particiones con un tamaño diferente a 2 (lo que hemos implementado aquí se conoce como Cooley-Tukey Radix FFT sobre la base de 2). También se pueden utilizar otros algoritmos FFT más complejos, incluidos enfoques fundamentalmente diferentes basados en datos de convolución (ver, por ejemplo, el algoritmo Blueshtein y el algoritmo Raider). La combinación de las extensiones y métodos anteriores puede conducir a FFT muy rápidas incluso en matrices cuyo tamaño no es una potencia de dos.
Aunque las funciones en Python puro son probablemente inútiles en la práctica, espero que proporcionen una idea de lo que está sucediendo en el fondo del análisis de datos basado en FFT. Como especialistas en datos, podemos hacer frente a la implementación de la "caja negra" de herramientas fundamentales creadas por nuestros colegas con una mentalidad más algorítmica, pero creo firmemente que cuanto más comprendamos acerca de los algoritmos de bajo nivel que aplicamos a nuestros datos, mejores prácticas lo haremos
Esta publicación fue escrita completamente en el Bloc de notas de IPython. El cuaderno completo se puede descargar
aquí o ver estáticamente
aquí .
Muchos pueden notar que el material está lejos de ser nuevo, pero, como nos parece, es bastante relevante. En general, escriba si el artículo fue útil. Esperando sus comentarios.