La verificación formal es la verificación de un programa o algoritmo utilizando otro.
Este es uno de los métodos más poderosos que le permite encontrar todas las vulnerabilidades en el programa o demostrar que no están allí.
Se puede ver una descripción más detallada de la verificación formal en el ejemplo de resolución del problema de
Wolf, Goat y col en mi artículo anterior.
En este artículo, pasaré de la verificación formal de tareas a los programas, y describiré
cómo convertirlos en sistemas de reglas formales automáticamente.
Para esto, escribí mi análogo de una máquina virtual, sobre principios simbólicos.
Analiza el código del programa y lo traduce a un sistema de ecuaciones (SMT), que ya se puede resolver mediante programación.
Dado que la información sobre los cálculos simbólicos se presenta en Internet de manera bastante fragmentaria,
Describiré brevemente de qué se trata.
Los cálculos de caracteres son una forma de ejecutar simultáneamente un programa en una amplia gama de datos y son la herramienta principal para la verificación formal de los programas.
Por ejemplo, podemos establecer las condiciones de entrada donde el primer argumento puede tomar valores positivos, el segundo negativo, el tercer cero y el argumento de salida, por ejemplo, 42.
Los cálculos simbólicos en una ejecución nos darán la respuesta, ¿es posible que obtengamos el resultado deseado y un ejemplo de un conjunto de tales parámetros de entrada? O la prueba de que no existen tales parámetros.
Además, podemos establecer los argumentos de entrada en general como sea posible, y seleccionar solo la salida, por ejemplo, la contraseña del administrador.
En este caso, encontraremos todas las vulnerabilidades del programa o obtendremos pruebas de que la contraseña de administrador es segura.
Puede notar que la ejecución clásica de un programa con datos de entrada específicos es un caso especial de uno simbólico.
Por lo tanto, mi VM de personaje también puede funcionar en el modo de emulación de una máquina virtual estándar.
En los comentarios al artículo anterior, puede encontrar una crítica justa de la verificación formal con una discusión de sus debilidades.
Los principales problemas son los siguientes:
- Explosión combinatoria, ya que la verificación formal finalmente descansa en P = NP
- Manejar llamadas al sistema de archivos, redes y otro almacenamiento externo es más difícil de verificar
- Errores en la especificación, cuando el cliente o programador concibió una cosa, pero no la describió con precisión en la declaración de trabajo.
Como resultado, el programa se verificará y cumplirá con las especificaciones, pero no hará lo que los creadores esperaban de él.
Como en este artículo considero principalmente la aplicación de la verificación formal en la práctica, todavía no golpearé mi frente contra la pared, y elegiré un sistema donde la complejidad algorítmica y la cantidad de llamadas externas sean mínimas.
Dado que los contratos inteligentes se ajustan a estos requisitos de la mejor manera, la elección recayó en los contratos RIDE de la plataforma Waves: no son completos para Turing, y su máxima complejidad está artificialmente limitada.
Pero los consideraremos únicamente desde el punto de vista técnico.
Además de todo, para cualquier contrato, la verificación formal será especialmente solicitada: como regla, es imposible corregir un error de contrato después de su lanzamiento.
Y el precio de tales errores puede ser muy alto, ya que grandes cantidades de fondos a menudo se almacenan en contratos inteligentes.
Mi máquina virtual de personajes está escrita en PHP y Python, y usa Z3Prover de Microsoft Research para resolver las fórmulas SMT resultantes.
En su núcleo se encuentra una poderosa búsqueda multi-transaccional, que
le permite encontrar soluciones o vulnerabilidades, incluso si requiere muchas transacciones.
Incluso
Mythril , uno de los marcos simbólicos más poderosos para buscar vulnerabilidades de Ethereum, agregó esta característica hace solo unos meses.
Pero vale la pena señalar que los contratos de ether son más complejos y tienen integridad de Turing.
PHP traduce el código fuente del contrato inteligente RIDE en un script python en el que el programa se presenta en forma de un sistema de estados y condiciones contractuales para sus transiciones compatibles con Z3 SMT:
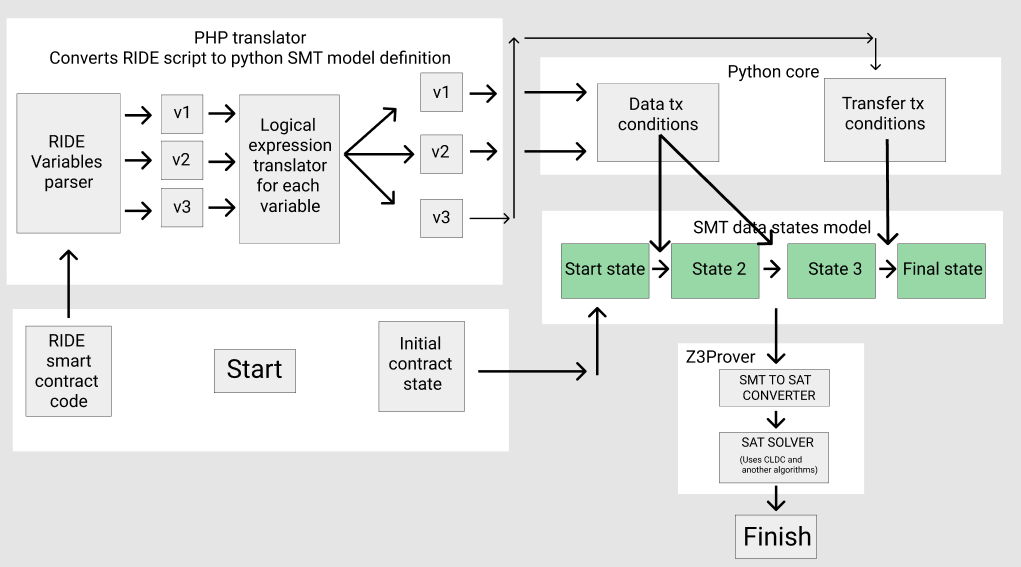
Ahora describiré lo que sucede dentro, con más detalle.
Pero primero, algunas palabras sobre el lenguaje de los contratos inteligentes RIDE.
Es un lenguaje de programación funcional y basado en expresiones que es perezoso según lo previsto.
RIDE se realiza de forma aislada dentro de blockchain y puede extraer y escribir información del almacenamiento asociado con la billetera del usuario.
Puede adjuntar un contrato RIDE a cada billetera y el resultado de la ejecución será solo VERDADERO o FALSO.
VERDADERO significa que el contrato inteligente permite la transacción y FALSO que lo prohíbe.
Un ejemplo simple: un script puede prohibir una transferencia si el saldo de la billetera es inferior a 100.
Como ejemplo, tomaré todos los mismos Wolf, Goat y Cabbage, pero ya presentados en forma de contrato inteligente.
El usuario no podrá retirar dinero de la billetera en la que se implementa el contrato hasta que reenvíe a todos al otro lado.
# let contract = tx.sender let human= extract(getInteger(contract,"human")) let wolf= extract(getInteger(contract,"wolf")) let goat= extract(getInteger(contract,"goat")) let cabbage= extract(getInteger(contract,"cabbage")) # -, 4 . # . match tx { case t:DataTransaction => # let newHuman= extract(getInteger(t.data,"human")) let newWolf= extract(getInteger(t.data,"wolf")) let newGoat= extract(getInteger(t.data,"goat")) let newCabbage= extract(getInteger(t.data,"cabbage")) #0 , , 1 let humanSide= human == 0 || human == 1 let wolfSide= wolf == 0 || wolf == 1 let goatSide= goat == 0 || goat == 1 let cabbageSide= cabbage == 0 || cabbage == 1 let side= humanSide && wolfSide && goatSide && cabbageSide # , . let safeAlone= newGoat != newWolf && newGoat != newCabbage let safe= safeAlone || newGoat == newHuman let humanTravel= human != newHuman # , - . let t1= humanTravel && newWolf == wolf + 1 && newGoat == goat && newCabbage == cabbage let t2= humanTravel && newWolf == wolf && newGoat == goat + 1 && newCabbage == cabbage let t3= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage + 1 let t4= humanTravel && newWolf == wolf - 1 && newGoat == goat && newCabbage == cabbage let t5= humanTravel && newWolf == wolf && newGoat == goat - 1 && newCabbage == cabbage let t6= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage - 1 let t7= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage let objectTravel = t1 || t2 || t3 || t4 || t5 || t6 || t7 # . # 1 0, # , # - side && safe && humanTravel && objectTravel case s:TransferTransaction => # human == 1 && wolf == 1 && goat == 1 && cabbage == 1 # case _ => false }
PHP, en primer lugar, extrae del contrato inteligente todas las variables en forma de sus claves y la variable correspondiente de la expresión lógica.
cabbage: extract ( getInteger ( contract , "cabbage" ) ) goat: extract ( getInteger ( contract , "goat" ) ) human: extract ( getInteger ( contract , "human" ) ) wolf: extract ( getInteger ( contract , "wolf" ) ) fState: human== 1 && wolf== 1 && goat== 1 && cabbage== 1 fState: wolf: goat: cabbage: cabbageSide: cabbage== 0 || cabbage== 1 human: extract ( getInteger ( contract , "human" ) ) newGoat: extract ( getInteger ( t.data , "goat" ) ) newHuman: extract ( getInteger ( t.data , "human" ) ) goatSide: goat== 0 || goat== 1 humanSide: human== 0 || human== 1 t7: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage t3: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage + 1 t6: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage - 1 t2: humanTravel && newWolf== wolf && newGoat== goat + 1 && newCabbage== cabbage t5: humanTravel && newWolf== wolf && newGoat== goat - 1 && newCabbage== cabbage t1: humanTravel && newWolf== wolf + 1 && newGoat== goat && newCabbage== cabbage t4: humanTravel && newWolf== wolf - 1 && newGoat== goat && newCabbage== cabbage safeAlone: newGoat != newWolf && newGoat != newCabbage wolfSide: wolf== 0 || wolf== 1 humanTravel: human != newHuman side: humanSide && wolfSide && goatSide && cabbageSide safe: safeAlone || newGoat== newHuman objectTravel: t1 || t2 || t3 || t4 || t5 || t6 || t7
PHP luego los convierte en una descripción del sistema Python compatible para Z3Prover SMT.
Los datos se envuelven en un ciclo donde las variables de almacenamiento obtienen el índice i, las variables de transacción índice i + 1, y las variables con expresiones establecen las reglas para la transición del estado anterior al siguiente.
Este es el corazón de nuestra máquina virtual, que proporciona un motor de búsqueda multi-transaccional.
fState: And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 ) final: fState[Steps] fState: wolf: goat: cabbage: cabbageSide: Or( cabbage[i] == 0 , cabbage[i] == 1 ) goatSide: Or( goat[i] == 0 , goat[i] == 1 ) humanSide: Or( human[i] == 0 , human[i] == 1 ) t7: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) t3: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] + 1 ) t6: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] - 1 ) t2: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage == cabbage[i] ) t5: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage == cabbage[i] ) t1: And( And( And( humanTravel[i] , wolf == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) t4: And( And( And( humanTravel[i] , wolf == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) safeAlone: And( goat[i+1] != wolf , goat[i+1] != cabbage ) wolfSide: Or( wolf[i] == 0 , wolf[i] == 1 ) humanTravel: human[i] != human[i+1] side: And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] ) safe: Or( safeAlone[i] , goat[i+1] == human[i+1] ) objectTravel: Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] ) data: And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] )
Las condiciones se ordenan y se insertan en una plantilla de script diseñada para describir el sistema SMT en python.
Plantilla en blanco import json from z3 import * s = Solver() Steps=7 Num= Steps+1 $code$
Para el último estado de toda la cadena, se aplican las reglas que se especifican en la sección de transacción de transferencia.
Por lo tanto, Z3Prover buscará un conjunto de condiciones que eventualmente le permitirán retirar fondos del contrato.
Como resultado, obtenemos automáticamente un modelo SMT totalmente funcional de nuestro contrato.
Puede ver que es muy similar al modelo de mi artículo anterior, que escribí manualmente.
Plantilla completa import json from z3 import * s = Solver() Steps=7 Num= Steps+1 human = [ Int('human_%i' % (i + 1)) for i in range(Num) ] wolf = [ Int('wolf_%i' % (i + 1)) for i in range(Num) ] goat = [ Int('goat_%i' % (i + 1)) for i in range(Num) ] cabbage = [ Int('cabbage_%i' % (i + 1)) for i in range(Num) ] nothing= [ And( human[i] == human[i+1], wolf[i] == wolf[i+1], goat[i] == goat[i+1], cabbage[i] == cabbage[i+1] ) for i in range(Num-1) ] start= [ human[0] == 1, wolf[0] == 0, goat[0] == 1, cabbage[0] == 0 ] safeAlone= [ And( goat[i+1] != wolf[i+1] , goat[i+1] != cabbage[i+1] ) for i in range(Num-1) ] safe= [ Or( safeAlone[i] , goat[i+1] == human[i+1] ) for i in range(Num-1) ] humanTravel= [ human[i] != human[i+1] for i in range(Num-1) ] cabbageSide= [ Or( cabbage[i] == 0 , cabbage[i] == 1 ) for i in range(Num-1) ] goatSide= [ Or( goat[i] == 0 , goat[i] == 1 ) for i in range(Num-1) ] humanSide= [ Or( human[i] == 0 , human[i] == 1 ) for i in range(Num-1) ] t7= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t3= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] + 1 ) for i in range(Num-1) ] t6= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] - 1 ) for i in range(Num-1) ] t2= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t5= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t1= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t4= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] wolfSide= [ Or( wolf[i] == 0 , wolf[i] == 1 ) for i in range(Num-1) ] side= [ And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] ) for i in range(Num-1) ] objectTravel= [ Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] ) for i in range(Num-1) ] data= [ Or( And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] ) , nothing[i]) for i in range(Num-1) ] fState= And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 ) final= fState
Después del lanzamiento, Z3Prover resuelve un contrato inteligente y nos muestra una cadena de transacciones, que nos permitirá retirar fondos:
Winning transaction chain found: Data transaction: human= 0, wolf= 0, goat= 1, cabbage= 0 Data transaction: human= 1, wolf= 0, goat= 1, cabbage= 1 Data transaction: human= 0, wolf= 0, goat= 0, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 0, cabbage= 1 Data transaction: human= 0, wolf= 1, goat= 0, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1 Transfer transaction
Además del contrato de reenvío, puede experimentar con sus propios contratos o probar este sencillo ejemplo, que se resuelve en 2 transacciones.
let contract = tx.sender let a= extract(getInteger(contract,"a")) let b= extract(getInteger(contract,"b")) let c= extract(getInteger(contract,"c")) let d= extract(getInteger(contract,"d")) match tx { case t:DataTransaction => let na= extract(getInteger(t.data,"a")) let nb= extract(getInteger(t.data,"b")) let nc= extract(getInteger(t.data,"c")) let nd= extract(getInteger(t.data,"d")) nd == 0 || a == 100 - 5 case s:TransferTransaction => ( a + b - c ) * d == 12 case _ => true }
Como esta es la primera versión, la sintaxis es muy limitada y pueden producirse errores.
En los siguientes artículos, planeo destacar el desarrollo posterior de VM y mostrar cómo es posible crear contratos inteligentes verificados formalmente con su ayuda, y no solo resolverlos.
Una máquina virtual simbólica está disponible en
http://2.59.42.98/hyperbox/Las fuentes están disponibles en github:
http://github.com/scp1001/hyperboxToda la lógica de VM está contenida en 2 archivos, hyperbox.php e hyperbox2.php