Un par de matemáticos basados en una teoría matemática poco conocida de hace 30 años demostraron que las superficies mínimas que se asemejan a una película de jabón aparecen en grandes cantidades en una amplia gama de figuras.

A finales de 2011,
Brian White ocasionalmente escuchó un golpe en la puerta de su oficina de Stanford. Afuera, en estos momentos, dos jóvenes matemáticos lo esperaban,
Fernando Coda Márquez y
Andre Nevis , que siempre tenían la misma pregunta: ¿tendrían White unos minutos para ayudarlos a descubrir una de las partes oscuras de una disertación poco conocida para varios cientos? páginas escritas hace treinta años?
La disertación, escrita por
John Pitts , presentó un poderoso mecanismo para construir superficies mínimas, estructuras similares a la película de jabón y las burbujas, dentro de una amplia gama de formas. Cuando se puede construir una superficie mínima en una figura, esta última permite estudiar la geometría del espacio que la rodea. Dichas superficies aparecen en varios problemas científicos, desde el estudio de los agujeros negros hasta el desarrollo de biomoléculas.
Y, sin embargo, todos estos años, la disertación de Pitts ha quedado fuera del alcance de la atención de los académicos, tal vez porque fue increíblemente difícil de leer. Márquez y Nevis estaban convencidos de que tenía un gran potencial. "Para nosotros era obvio que esta teoría estaba completamente subestimada y pasó desapercibida", dijo Nevis, quien ahora es profesor en la Universidad de Chicago.
Aunque White nunca preguntó a la pareja por qué estaban interesados en el trabajo de Pitts, cada vez declararon que su interés era "puramente académico", dijo Nevis. Sin embargo, tenían un objetivo definido: probar la hipótesis de Wilmore hace 50 años, que aborda el problema de encontrar la mejor forma de rosquilla posible (detalles más adelante). Después de tres meses de luchar con las ideas de la disertación de Pitts, Márquez y Nevis
lograron su objetivo , obteniendo muchos premios y críticas positivas.
Pero en los últimos años, han podido impulsar las ideas de Pitts mucho más. Pitts, con su curador, Frederick Almgren, encontró una manera de asegurarse de que cada figura en un pequeño número de dimensiones tenga al menos una superficie mínima. Ahora, Márquez y Nevis, utilizando la cohorte de jóvenes matemáticos reunidos a su alrededor, basados en las ideas de Almgren y Pitts, han demostrado que, en el caso general, estas formas deben contener muchas superficies mínimas, infinitas superficies que se apiñan y apiñan en todos los rincones de las figuras. "Este es un gran avance", nos escribió en un correo electrónico la famosa geómetra
Karen Uhlenbeck de la Universidad de Texas.
"Se necesita mucho esfuerzo para crear una superficie mínima única", dijo
Richard Shoin, de la Universidad de California, Irvine, quien asesoró a Nevis hace unos 15 años. "El hecho de que haya tantos es increíble".
Este renacimiento de la teoría de Almgren y Pitts ha llevado a una explosión de actividad en los últimos años. "Los resultados son tan rápidos y en cantidades tan grandes que es difícil hacer un seguimiento de ellos", dijo White. "Me parece muy interesante y maravilloso".
Marcar la cordillera
Sumerja el alambre curvo en una solución de jabón, o sople una burbuja de jabón, y el líquido formará rápidamente la superficie del área más pequeña posible. La geometría de estas superficies mínimas ha ocupado a los matemáticos durante cientos de años. Aparecen en varios campos, desde la arquitectura, donde la superficie mínima inspira el diseño de techos y otras estructuras, hasta la creación de micropartículas para la entrega de medicamentos. Hace cinco años, cuando un equipo de científicos
creó moléculas porosas capaces de transportar drogas u hormonas dentro de sí mismas, descubrieron que algunas moléculas tomaban la forma de un
giroides , una superficie que se repetía sin cesar, algunas de las cuales se asemejan a una película de jabón.
Técnicamente, los matemáticos consideran solo las películas de jabón en un alambre como superficies con una superficie mínima, pero no burbujas de jabón, porque en un espacio abstracto donde no hay moléculas de aire, la burbuja se desinflaría hasta un punto. Sin embargo, la película en el cable no satisface completamente a los matemáticos. Su parte interna es una superficie lisa, pero su cable se rompe bruscamente. Es lógico pensar si es posible extender esta superficie más allá de los límites de los cables para que siga pareciendo una película de jabón en cada área individual. A veces esto es posible, y la superficie se extiende hasta el infinito. A veces la superficie regresa y se cruza torpemente consigo misma, o encuentra otras dificultades.
 Gyroid: un tipo de superficie mínima que se produjo durante el diseño de micropartículas para la administración de fármacos.
Gyroid: un tipo de superficie mínima que se produjo durante el diseño de micropartículas para la administración de fármacos.En el espacio ordinario, esto agota todas las posibilidades. Pero los matemáticos y otros científicos a menudo consideran otros mundos que son diferentes del espacio tridimensional infinito al que estamos acostumbrados, curvos o finitos, como las analogías tridimensionales de una esfera o superficie de un toro. Tales figuras tienen nuevas posibilidades interesantes: superficies mínimas que se doblan sobre sí mismas y se bloquean en una figura final cerrada que no requiere soporte de alambre.
En la teoría de la relatividad, estas superficies mínimas finitas juegan el papel del horizonte de eventos de los agujeros negros. Y si se pueden encontrar en cualquier figura, esto ayuda a los matemáticos a considerar su geometría desde diferentes lados: dan una plantilla para cortar la figura (o
colector ) en piezas potencialmente más simples, indican áreas de curvatura positiva dentro del colector, en secciones, curvarse hacia adentro, como una esfera o un agujero negro, en lugar de curvarse hacia afuera.
"Sabemos poco acerca de los colectores con curvatura positiva", dijo Shoin.
Sin embargo, a menudo es difícil demostrar la existencia de una superficie mínima dentro de una figura. Para entender por qué, considere una versión bidimensional de este problema. La cuestión de encontrar la superficie mínima tiene sentido en cualquier dimensión: los matemáticos simplemente consideran que la superficie es una forma cuya dimensión es una menos que el espacio en el que vive. Entonces, en un mundo bidimensional, las curvas "geodésicas" formadas por los caminos más cortos que conectan puntos cercanos serán la superficie mínima.
Para algunas figuras bidimensionales, encuentre fácilmente curvas geodésicas cerradas en un bucle finito. Tome la superficie de un toro, ni siquiera necesariamente uniforme y simétrico; deje que tenga irregularidades y protuberancias. Si envolvemos una rosquilla con una banda elástica que pasa por su centro, podemos imaginar cómo la apretamos y cambiamos a varias posiciones posibles. Uno de ellos será el más corto, por definición, será una curva geodésica.
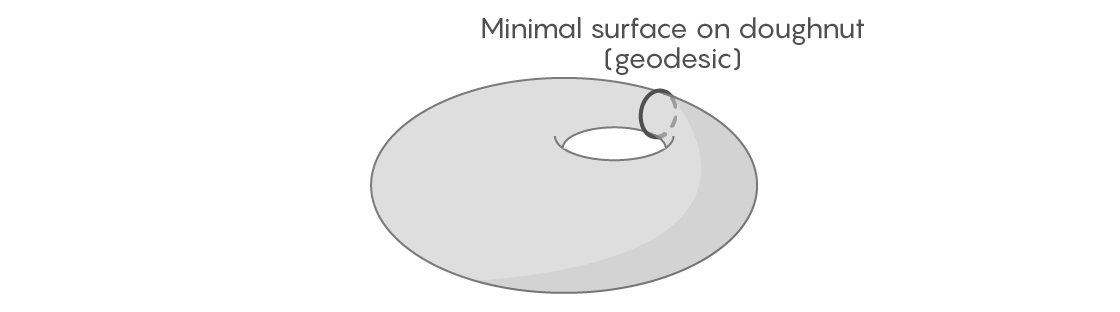
Pero si la esfera es nuestra figura, este enfoque ya no funcionará. En una esfera perfectamente plana, es fácil encontrar una curva geodésica: será el ecuador y otros círculos completos. Pero en una esfera desigual, por ejemplo, en la superficie de la Tierra, no está claro a dónde van las curvas geodésicas y si alguna de ellas está cerrada en un bucle. Puedes imaginar cómo envolvemos la tierra con una banda elástica, como en el caso de una dona. Pero si comienza a moverlo, tratando de acortarlo, se reducirá a un punto, porque a diferencia de una rosquilla, la esfera no tiene un agujero para que el elástico se adhiera.
Sin embargo, este fiasco con una banda elástica está plagado del germen del éxito. Si el ecuador de una esfera redonda es interceptado por una banda elástica, entonces la única forma de desplazarlo, para agregarle ondas, lo hará más largo. Si lo mueve de manera diferente, hacia arriba o hacia abajo a una nueva latitud, se acortará. Por lo tanto, el ecuador será la curva más corta desde un punto de vista y la más larga desde el otro.
Esto hace que el ecuador se relacione con la silla del paso de montaña, el punto más alto en un lado (desde el camino a través de las montañas) y el más bajo en el otro (desde el camino hasta los picos cercanos). Y esto no es solo una analogía débil: como regla, las superficies mínimas resultan ser tales, pero sus cadenas montañosas viven en un mundo que es mucho más difícil de visualizar.
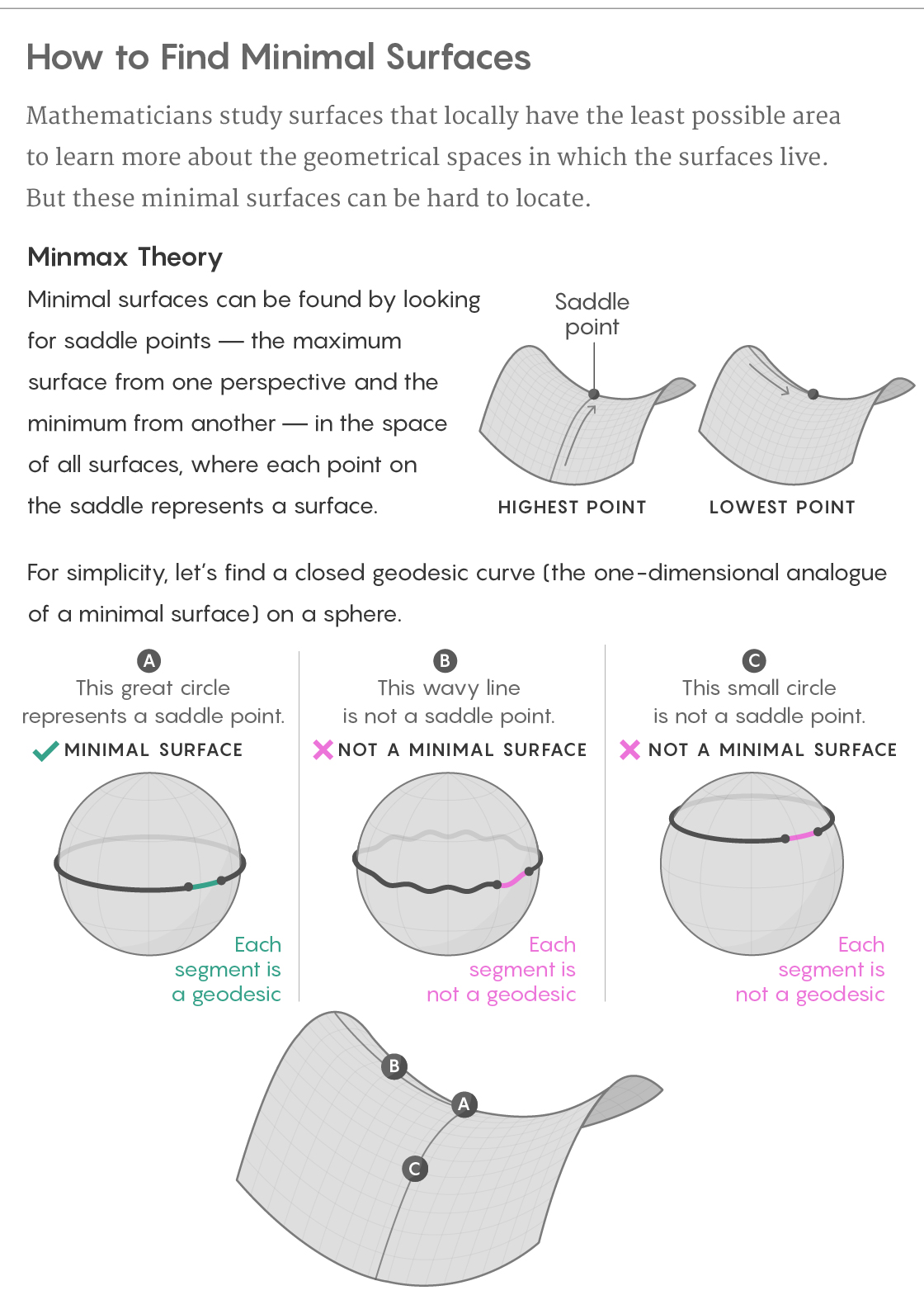
Al determinar la superficie mínima de una figura, podemos considerar un nuevo mundo que consta de todas las superficies finitas posibles existentes dentro de esta figura; la llamaremos la "superficie de las superficies". Cada punto del espacio de superficie corresponde a toda la superficie en su totalidad en la figura original. Entonces podemos considerar el área de cada superficie como la altura del punto correspondiente en el espacio de superficies, como resultado de lo cual nuestro mundo tendrá una topografía natural. La búsqueda de superficies mínimas en la figura original se convierte en la búsqueda de monturas en el espacio de superficie.
En 1917, George David Birkhoff
utilizó este enfoque para mostrar que cualquier esfera, irregular o lisa, debe tener una curva geodésica cerrada. Aproximadamente seis décadas después, Almgren y Pitts ampliaron magistralmente las ideas de Birkhoff al marcar la topografía de la superficie de todas las figuras finitas en dimensiones de tres a siete, y luego usaron esta topografía para demostrar que tales figuras siempre tienen al menos una superficie mínima cerrada. La
disertación de Pitts de 1981 sobre esta teoría de Minmax, llamada así porque el sillín es un mínimo y un máximo, fue "absolutamente increíble", dijo Nevis.
Sin embargo, fue extremadamente complejo. Pocas personas entendieron los matices de la teoría, y algunos matemáticos que la estudiaron afirmaron que no estaba completamente confirmada, dijo Shoin. "No creo que haya ninguna duda de que fue extremadamente interesante e importante", dijo. "Pero no estaba claro qué tan lleno estaba".
El trabajo sobre la teoría de Minmax gradualmente quedó en nada. "El trabajo de Pitts ha sido olvidado por la comunidad matemática durante unos 30 años", dijo Nevis. No fue resucitada hasta que Nevis y Márquez se conocieron en 2006 en el ascensor del edificio matemático de la Universidad de Princeton.
Sobre el puerto de montaña
En ese momento, Márquez llegó a Princeton para dar una conferencia; Nevis consiguió un trabajo allí poco después de defender un doctorado. Ambos tenían el portugués como lengua materna (Márquez era de Brasil y Nevis era de Portugal), y encontraron fácilmente un idioma común. "Luego hablé con él por primera vez, pero él habló conmigo como si hubiéramos sido amigos durante 10 años", recuerda Márquez, ahora profesor de Princeton.
Luego descubrieron que discutir ideas matemáticas era igual de natural para ellos. Tienen diferentes estilos: Márquez es más tranquilo y Nevis es más intenso. Pero esto sirvió como una ventaja para ellos. "Es muy raro encontrar a alguien que te complemente tan bien", dijo Márquez.
Ambos estaban ansiosos por encontrar algún problema matemático complejo en el que pudieran estar inmersos. Durante varios años, la pareja lanzó ideas cada vez que sus caminos se cruzaron para "ver qué se retrasó", dijo Nevis. "Teníamos un millón de ideas y, como resultado, una de ellas se filtró y se convirtió en algo formado".
El problema filtrado resultó ser el famoso problema de la "hipótesis de Wilmore". Ella sugiere encontrar una forma de toro que minimice la magnitud conocida como la energía de Willmore, que, en términos generales, mide la diferencia entre una forma dada y una esfera circular. En 1965, Wilmore
sugirió que sería la dona más redonda de una forma particularmente simétrica, conocida como
el toro de Clifford , sin embargo, a pesar de muchos intentos, la hipótesis no se pudo probar a nadie.
 Márquez (izquierda) y Nevis
Márquez (izquierda) y NevisMárquez y Nevis desarrollaron un enfoque prometedor, pero para que funcionara, necesitaban el último ingrediente: la teoría minimax. Pensaron que dominar esta teoría y escribir el trabajo final tomaría de dos a tres semanas, hasta que abrieron el libro de Pitts. “Nos sorprendió, ¿de qué se trata todo esto? - dijo Nevis "El libro estaba increíblemente seco".
Los teoremas separados crecieron en muchas páginas, y esto fue solo una descripción de los teoremas, no su prueba. El teorema principal era simplemente difícil de encontrar. "Recuerdo cómo Fernando llegó a mi oficina y dijo: ¡Encontré la declaración del teorema!" - dijo Nevis
 Thor Clifford
Thor CliffordCuando se atascaron, jugaron al póker y le pidieron ayuda a White, una de las pocas personas que entendía la mayor parte del trabajo de Pitts (aunque White mismo describió estas conversaciones como "ciegas, ciegas"; el mismo Pitts, profesor de la Universidad de Texas A&M, se graduó escribir obras sobre la teoría de minmax hace unas décadas). "Estábamos increíblemente motivados, por lo que pudimos avanzar", recuerda Nevis. "Pero esa no fue una tarea para los débiles de corazón".
Cuando Márquez y Nevis terminaron su prueba de la hipótesis de Wilmore, entendieron la teoría de Minmax mejor que cualquier otro matemático. Estaban convencidos de que su potencial se extiende mucho más allá de la declaración misma de la hipótesis. "Sabíamos que teníamos una teoría muy poderosa", dijo Nevis. - Cada vez, utilizando el método para probar un cierto resultado que ha permanecido abierto durante mucho tiempo, comprende que hay algo en él. Esto sugiere que vale la pena seguir investigando más ".
El diagrama minmax de Almgren y Pitts produce no solo una silla de montar, sino un número infinito de ellas. En teoría, esto debería corresponder a un número infinito de superficies mínimas de la forma original. Pero Almgren y Pitts no pudieron demostrar que las superficies mínimas obtenidas de esta manera fueran diferentes. Por lo tanto, lo único que definitivamente se podía decir era que cada figura tenía al menos una superficie mínima.
Después de eso, "el desarrollo del tema prácticamente se ha detenido", dijo Nevis. "Fue el mejor resultado por un período de más de 30 años".
Se necesitaba un nuevo ingrediente, y Márquez y Nevis lo encontraron. La lista interminable de superficies mínimas, como se mostró en 2016, se comporta igual que las frecuencias del tambor.
El matemático alemán Weil en 1911 demostró que las frecuencias fundamentales del tambor tienen una propiedad inesperada: en términos generales, las frecuencias altas dependen solo del volumen del tambor y no de su forma. Márquez y Nevis, junto con
Eugene Lekumovich del Instituto de Tecnología de Massachusetts,
mostraron que las superficies Minmax satisfacen una ley matemática similar a la ley de las frecuencias de tambor. En particular, las áreas de superficie están determinadas aproximadamente por la cantidad de espacio en el que viven, y no por su forma.
Este resultado, que puso fin a la hipótesis presentada hace varias décadas, permitió a Márquez y Nevis
mostrar en 2017, esta vez fueron ayudados por
Kay Air de la Universidad de Tokio, que para la mayoría de las cifras, la lista de minmax contiene un número infinito de diferentes superficies mínimas. Además, mostraron que estas superficies son "densas": aparecen al lado de cada punto en el espacio circundante. La intuición que respalda esta conclusión es que para que el volumen del espacio determine las áreas de ubicación de las superficies mínimas, este último debe de alguna manera "ver" todo el volumen. Y esto "dice que estos muchachos están en toda su diversidad", dijo Márquez.
Un par de meses después, esta pareja, junto con la estudiante graduada de Marques,
Antoine Sun , demostró que si revisa la lista de superficies mínimas, verá que
llenan el espacio de manera uniforme , lo que los matemáticos llaman "equidistribución".
"Cuando escuché que estaban distribuidos por igual, me sorprendió", dijo White. "Parecía que la gente no debería haber podido probar tal resultado durante mi vida".
En los últimos años, varios matemáticos más se han unido a la pregunta. Por ejemplo, en enero,
Xin Zhou, de la Universidad de California en Santa Bárbara, basándose en el trabajo previo de Márquez y Nevis,
demostró que para la mayoría de las figuras todas las superficies mínimas en la lista de Almgren y Pitts son diferentes entre sí, lo que pone un buen punto en este tema. "Esto cierra muy bien este tema, abierto desde los días de Almgren y Pitts en los años 80", dijo White.
Esta familia de resultados tiene en cuenta casi todas las figuras en dimensiones de tres a siete, con la excepción de las formas más suaves, sin importar cuán contradictorias sean. Pero en junio pasado, Sunn pudo
demostrar que cada figura en estas dimensiones, incluidas las más redondeadas, tiene infinitas superficies mínimas cerradas, lo que confirmó otra hipótesis que tiene varias décadas de antigüedad.
Todavía no está claro si la densidad y la equidistribución se comportarán de manera tan uniforme, como tampoco cómo la teoría minmax no funciona en múltiples compactos, o en ocho o más dimensiones (sin embargo, el
nuevo trabajo también ha tenido cierto éxito aquí). Los matemáticos predicen que podremos responder muchas preguntas antes de lo que parecía.
"Todo se está desarrollando extremadamente rápido", dijo Nevis. "Cada semana miro el sitio con preimpresiones arxiv, y veo cómo alguien decidió algo más".
Desde un punto de vista, estas obras marcan el final, o el final, de una historia que ha permanecido en su estado inacabado durante casi cuatro décadas. Pero este también es un nuevo comienzo: los matemáticos apenas comienzan a comprender que estas nuevas ideas sobre superficies mínimas pueden contarnos sobre los espacios en los que viven.
"Puedo suponer que pronto aparecerán otras formas interesantes de aplicar este conocimiento, pero qué, exactamente, definitivamente no puedo decir", dijo Shoin.
"Estoy seguro de que esta será una de las direcciones principales en geometría".