Proyecto: "Tipo de cambio absoluto"
Introduccion
Sobre el proyecto
El proyecto " Tipo de cambio absoluto " se dedica al análisis de los tipos de cambio emparejados, la asignación de los tipos de cambio absolutos de ellos y su análisis.
En el marco del proyecto, se obtuvo una metodología para la conversión de tasas de pares a tasas de cambio absolutas. Para esto, se define la moneda absoluta ABS. Todas las monedas disponibles se expresan en términos de ABS.
El proyecto explora las propiedades de los cursos absolutos. Se investigan diversas aplicaciones de los tipos de cambio absolutos.
¿Por qué es esto ...?
Hasta la fecha, ya se han publicado varios artículos sobre la aplicación del método de tipo de cambio absoluto. Traigo los dos últimos.
El artículo " Un estudio de la conexión de las monedas mundiales a través de la correlación de los tipos de cambio absolutos " describe una de las aplicaciones de la tecnología de los tipos de cambio absolutos. Se da un método formal para calcular la relación entre las diferentes monedas.
El artículo " El método de cartera de Markowitz aplicado al mercado de divisas " describe la tecnología previamente inaccesible para optimizar la cartera de divisas.
La investigación no se detiene en estas dos aplicaciones. Se están probando otras aplicaciones tecnológicas. Si los lectores tienen sus propias visiones de otros usos posibles, se pueden escribir en la discusión del artículo. Se proporcionan enlaces a sitios de discusión.
Metodología para la obtención de cursos absolutos.
En el artículo " De pares de divisas a tipos de cambio absolutos " se ofrece una descripción detallada de la tecnología.
El método se basa en el análisis de la presentación de cursos emparejados. Un tipo de cambio de par es la relación entre el valor de una moneda y el valor de otra. Y si introduce algunos ABS de moneda absoluta universal, entonces tiene lugar la siguiente transformación.
EUR/USD= fracEURUSD= fracEUR/ABSUSD/ABS
Un tipo de cambio de par es la razón de dos tipos absolutos.
Para obtener cursos absolutos, primero debe prologarithm esta ecuación.
ln(EUR/USD)=ln( fracEUR/ABSUSD/ABS)=ln(EUR/ABS)−ln(USD/ABS)
En consecuencia, se puede ver que los logaritmos de las tasas de pares están linealmente relacionados con los logaritmos de las tasas de cambio absolutas. Y eso significa que puede buscar una transformación lineal simple entre ellos. Los logaritmos de los cursos absolutos se pueden multiplicar por la matriz de conversión directa y obtener los logaritmos de los cursos emparejados.
ln(Xabs) vecesMpr=ln(Xpar)
Y debemos esperar que haya una transformación lineal inversa para la transición de cursos de pares a cursos absolutos.
ln(Xpar) vecesMobr=ln(Xobr)
En consecuencia, toda la metodología para obtener cursos absolutos está escrita de la siguiente manera.
Xabs=eln(Xpar) vecesMobr
Solo necesita registrar los cursos emparejados, multiplicarlos por la matriz inversa y aplicar el exponente.
Sobre problema
Se describió anteriormente cómo obtener cursos absolutos de dobles. Esto se realiza mediante una transformación lineal de las tasas de pares logarítmicos y el retorno a través del exponente.
La conversión lineal directa de tasas absolutas a pareadas se realiza utilizando una matriz directa. Conseguirlo es muy simple. Consiste en ceros, unos y menos unos ("0" significa que no hay relación par / moneda, "+1" significa la moneda en el numerador del par, "-1" significa la moneda en el denominador del par). Debajo puedes verlo.
El mayor problema es obtener la matriz inversa (más precisamente, debe usar la transformación pseudo-inversa ). Con su ayuda, puedes pasar de cursos en pareja a cursos absolutos. Pero obtener esta matriz no es trivial debido a la degeneración de la matriz de transformación directa.
En el artículo anterior, se da una descripción de un método para obtener dicha matriz. En el artículo " Detalles de la transición de los tipos de cambio par (relativos) a absolutos. Trabajar en errores ”revela un método para obtener cursos absolutos. En el experimento, utilizamos la técnica de transición a componentes linealmente independientes. Por lo tanto, fue posible deshacerse de la degeneración en la transformación pseudo-inversa.
Método del presente experimento.
En este artículo, se propone otro método para evitar la degeneración en la matriz de transformación directa. Actualmente, los cursos emparejados son proporcionados por el RBC . Hay 88 pares de monedas para la exportación. Para ellos, existe la siguiente matriz de transformación directa.
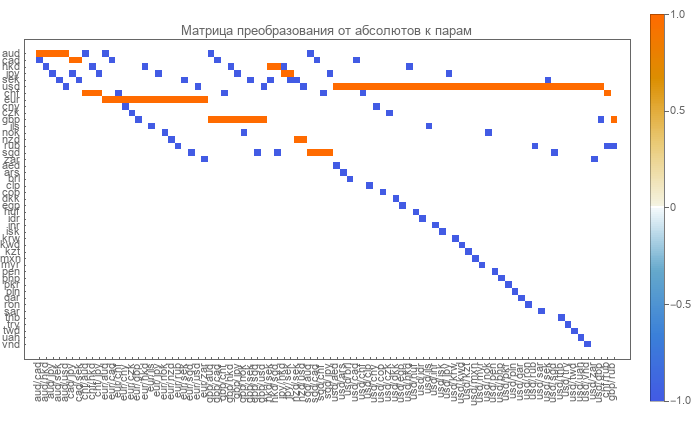
Ceros blancos, azul -1 y rojo son unidades. Pero es degenerado. Es decir no producirá una matriz inversa.
Durante el experimento anterior, fue posible notar que una matriz diagonalmente similar tiene una transformación inversa. En consecuencia, se hizo una propuesta para cambiar a tasas cruzadas y una matriz de transformación no degenerada .
Todo el cálculo se realizó en el sistema Wolfram Mathematica . El sistema le permite recibir cursos cruzados directamente dentro del sistema .
Detalles del experimento (pequeño ejemplo)
Hay un total de 45 monedas. Para mayor claridad, primero consideramos el caso con un pequeño número de monedas y pares de divisas. El cálculo está disponible a través del enlace en Wolfram Cloud .
Lista de monedas y pares de divisas.
Se seleccionaron las siguientes 10 monedas: AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK. De estos, se determinaron 9 pares de divisas: AUD / CAD, CAD / HKD, HKD / JPY, JPY / SEK, SEK / USD, USD / CHF, CHF / EUR, EUR / CNY, CNY / CZK.
Matriz de conversión directa
La matriz de transformación directa tiene la siguiente forma.

La versión coloreada se ve así.

El tamaño de la matriz es 10x9. El rango de la matriz es 9. La matriz no está degenerada. Puedes buscar libremente lo contrario.
Matriz de transformación inversa de emparejado a absoluto
Como resultado de aplicar el método de transformación pseudo-inversa, obtenemos la matriz inversa.

En forma coloreada así.

El tamaño de la matriz inversa es de 9x10.
Comprobación de matriz inversa
Antes de continuar, verifique la matriz resultante. Para hacer esto, multiplicamos la matriz inversa por la línea recta. El resultado es el siguiente.

Y en forma coloreada.
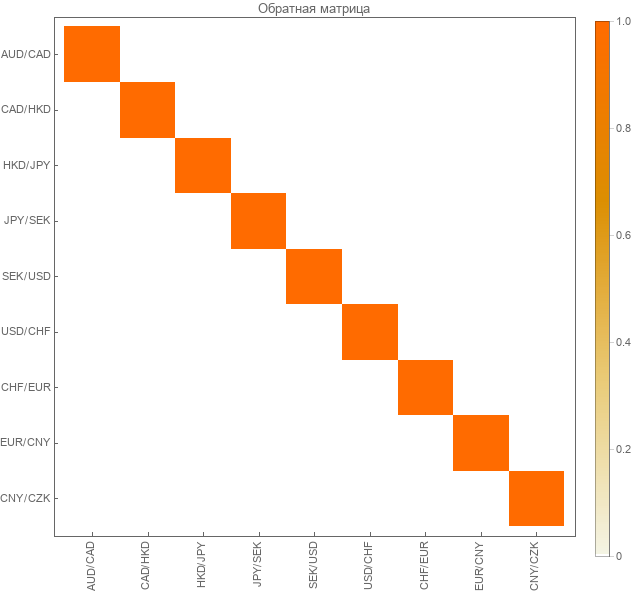
Realmente tengo la unidad de matriz diagonal . Entonces lo contrario es cierto.
En un experimento anterior , probamos el método para obtener tasas absolutas. Para esto, a partir de los cursos absolutos obtenidos, los cursos de pares se restauraron mediante la matriz de conversión directa. Luego comparamos los cursos emparejados restaurados con los originales y observamos el error. En nuestro caso, el error en dicha verificación estará dentro de los límites de precisión de la máquina.
Pruebas en cursos reales.
Ahora veamos los resultados en datos reales. Tomemos cotizaciones reales de las tasas cruzadas de divisas de pares y calculemos las tasas absolutas para ellas.
Tomamos cursos cruzados diarios durante 30 días del 28/03/2019 al 27/04/2019.
Tasas de pares de divisas
Aquí hay una matriz de tipos de cambio emparejados. Estas son las columnas de pares de divisas para los siguientes pares AUD / CAD, CAD / HKD, HKD / JPY, JPY / SEK, SEK / USD, USD / CHF, CHF / EUR, EUR / CNY, CNY / CZK.

Aquí está el gráfico de uno de los pares de divisas.

Los valores promedio para cursos en pareja fueron los siguientes.
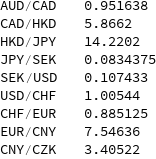
Ahora intentemos evaluar la variabilidad de los datos. Para hacer esto, use la desviación estándar . Pero para la estandarización, lo dividimos por el valor promedio. Mostramos los resultados en el gráfico.
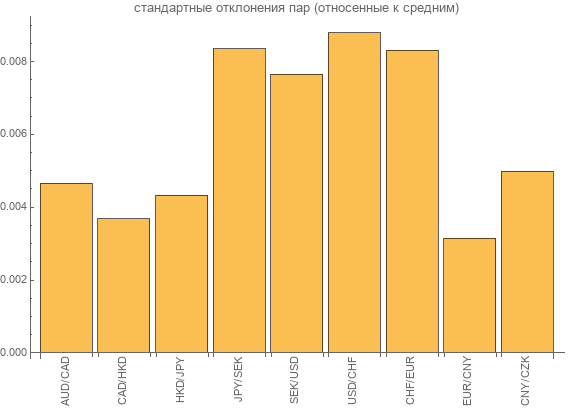
Como puede ver, las desviaciones estándar para cada par de divisas están en el rango de 0, 2% - 0, 9% de los valores promedio de las tasas de pares.
Cursos Absolutos
Ahora calculamos cursos absolutos para pares (la metodología se describe en la sección Metodología para obtener cursos absolutos). Después de los cálculos, obtenemos la siguiente serie de datos.
Estas son columnas de cambio absoluto para las siguientes monedas AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK.

Aquí hay un gráfico del tipo de cambio absoluto de una de las monedas.
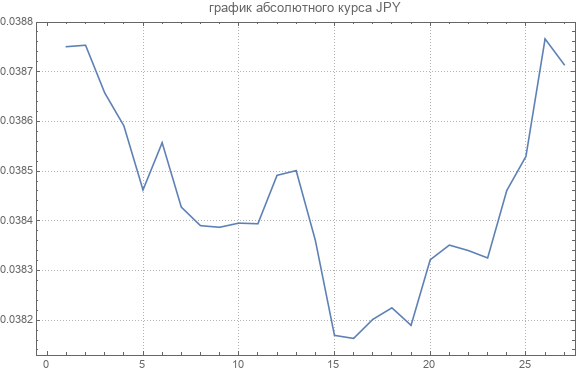
Los valores promedio para cursos absolutos son los siguientes.

Estimamos la variabilidad de los tipos de cambio absolutos.

Las desviaciones estándar para las tasas absolutas de cada moneda están en el rango de 0, 2% - 0, 7% de los valores promedio de las tasas absolutas. Y esto es consistente con los datos de los pares de divisas.
Resultados en todas las monedas
Ahora considere los resultados en todas las monedas disponibles. La fuente de cálculo está disponible aquí .
Lista de monedas y pares de divisas.
La lista completa contiene las siguientes 45 monedas: AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK, GBP, ILS, NOK, NZD, RUB, SGD, ZAR, AED, ARS, BRL, CLP, COP , DKK, EGP, HUF, IDR, INR, ISK, KRW, KWD, KZT, MXN, MYR, PEN, PHP, PKR, PLN, QAR, RON, SAR, THB, PRUEBA, TWD, UAH, VND. Se seleccionaron los siguientes 44 pares de divisas: AUD / CAD, CAD / HKD, HKD / JPY, JPY / SEK, SEK / USD, USD / CHF, CHF / EUR, EUR / CNY, CNY / CZK, CZK / GBP, GBP / ILS, ILS / NOK, NOK / NZD, NZD / RUB, RUB / SGD, SGD / ZAR, ZAR / AED, AED / ARS, ARS / BRL, BRL / CLP, CLP / COP, COP / DKK, DKK / EGP, EGP / HUF, HUF / IDR, IDR / INR, INR / ISK, ISK / KRW, KRW / KWD, KWD / KZT, KZT / MXN, MXN / MYR, MYR / PEN, PEN / PHP, PHP / PKR, PKR / PLN, PLN / QAR, QAR / RON, RON / SAR, SAR / THB, THB / TRY, TRY / TWD, TWD / UAH, UAH / VND.
Matriz de conversión directa
Tenemos una matriz de transformación directa de tamaño 45 por 44. Su rango es 44.
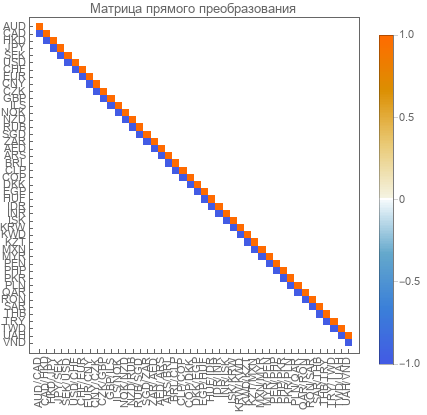
Matriz de transformación inversa
La matriz inversa es el resultado de aplicar pseudo-transformación inversa. El tamaño de la matriz es de 44 por 45.
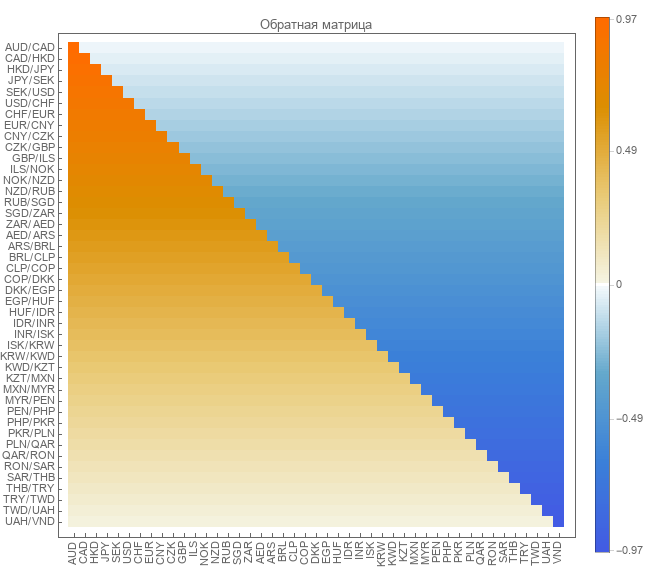
Comprobación de matriz inversa
Después de multiplicar la matriz inversa por la línea recta, obtuvimos la matriz de identidad.
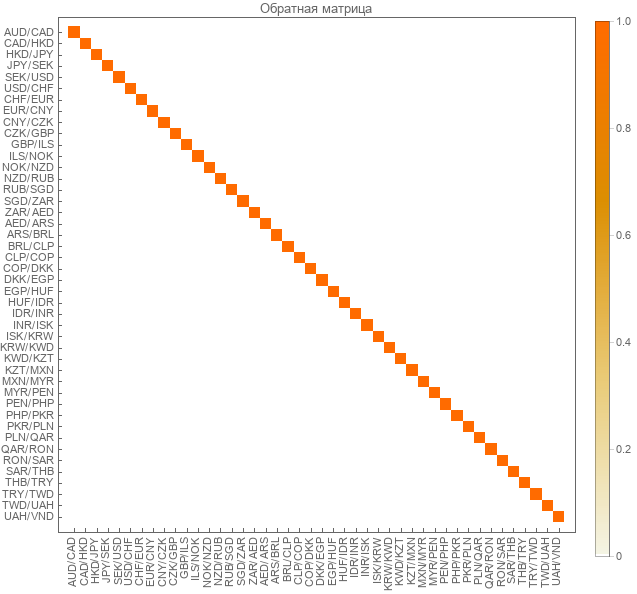
Pruebas en cursos reales.
Cargó 44 pares de tipos de cambio cruzados. Un ejemplo de uno se da en el siguiente gráfico.
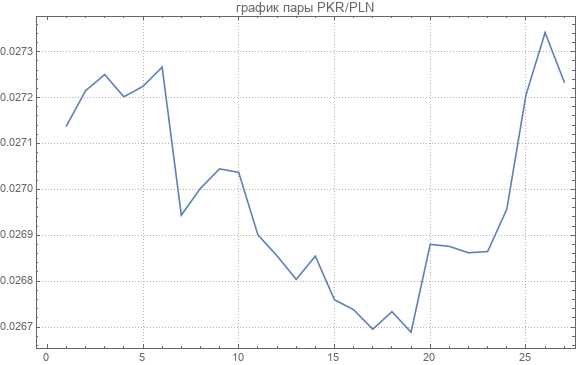
Aquí están los tipos de cambio promedio para cada par de divisas.
AUD / CAD 0.951638
CAD / HKD 5.8662
HKD / JPY 14.2202
JPY / SEK 0.0834375
SEK / USD 0,107433
USD / CHF 1.00544
CHF / EUR 0.885125
EUR / CNY 7.54636
CNY / CZK 3.40522
CZK / GBP 0.0335481
GBP / ILS 4.69022
ILS / NOK 2.38106
NOK / NZD 0.173451
NZD / RUB 43.5338
RUB / SGD 0.0209621
SGD / ZAR 10.4641
ZAR / AED 0.259015
AED / ARS 11.7136
ARS / BRL 0.0907021
BRL / CLP 171.256
CLP / COP 4.72058
COP / DKK 0.00210715
DKK / EGP 2.60095
EGP / HUF 16.5291
HUF / IDR 49.5307
IDR / INR 0.00490364
INR / ISK 1.73912
ISK / KRW 9.44975
KRW / KWD 0.000266945
KWD / KZT 1248.05
KZT / MXN 0.050062
MXN / MYR 0.216251
MYR / PEN 0.803967
PEN / PHP 15.7631
PHP / PKR 2.71475
PKR / PLN 0.0269842
PLN / QAR 0.954411
QAR / RON 1.16298
RON / SAR 0.885697
SAR / THB 8.48908
THB / TRY 0.179564
PRUEBA / TWD 5.39876
TWD / UAH 0.871089
UAH / VND 863.675
Para cada par de divisas, observamos la variabilidad como en el experimento anterior.

La desviación estándar para todos los pares de divisas varía de 0.2% a 2.5% del promedio.
Después del recuento obtenemos tasas absolutas. Aquí hay un gráfico de la tasa absoluta de una de las monedas.
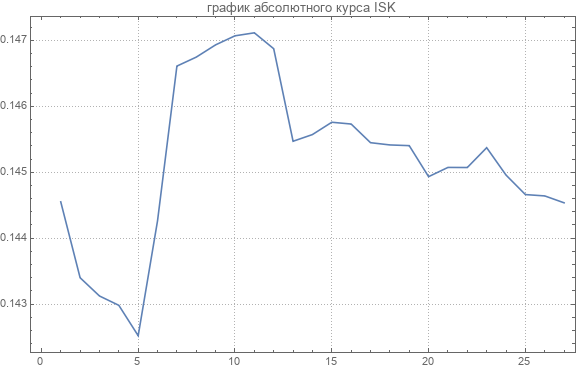
Los valores promedio de las tasas absolutas fueron los siguientes.
AUD 12.4626
CAD 13.096
HKD 2.23247
JPY 0.156996
1.88165 SEK
USD 17.5149
17,42 CHF
19,6824 EUR
CNY 2.60821
0,765955 coronas checas
GBP 22.832
ILS 4.86814
2,04455 NOK
NZD 11.7884
RUB 0.270822
SGD 12.9197
ZAR 1.23485
AED 4.76765
ARS 0.407218
BRL 4.49018
CLP 0.0262207
COP 0.0055548
DKK 2.63619
EGP 1.01359
0,0613224 HUF
IDR 0.00123809
INR 0.25249
ISK 0.145194
KRW 0.0153652
KWD 57.5605
KZT 0.0461203
MXN 0.921362
MYR 4.26106
PEN 5.30007
PHP 0.336241
PKR 0.123862
PLN 4.59025
QAR 4.8096
RON 4.1356
SAR 4.66938
THB 0.550046
PRUEBE 3.06473
TWD 0.567676
UAH 0.651731
VND 0.000754602
La variabilidad de las tasas absolutas se puede estimar mediante el diagrama.

La desviación estándar de todas las tasas absolutas varía de 0.2% a 2.5% del promedio. Lo cual es consistente con los datos de los pares de divisas.
Conclusiones
El experimento con la obtención de cursos absolutos de cursos cruzados emparejados fue un éxito. Se ha obtenido un nuevo método para calcular las tasas absolutas. El método funciona y es fácilmente aplicable. Para futuras investigaciones, es bastante fácil recibir cursos absolutos.
La precisión del método está limitada solo por la precisión de los cursos cruzados emitidos.
Desafortunadamente, las tasas cruzadas de código abierto no se pueden encontrar en la red. Y en consecuencia, este método no se puede aplicar en el sitio. Pero en la comparación inicial de los cursos absolutos del sitio y los obtenidos en el presente experimento, las diferencias se revelaron solo en el cuarto decimal. Realizaremos una comparación detallada en los siguientes trabajos.
La última versión de este artículo en formato PDF se puede descargar aquí .
Enin A.V.
Orenburg
02/05/2019