Hola Habr!
Esta publicación me pareció interesante: obtenemos
tipos de cambio absolutos de los tipos de cambio cruzados por pares y quería probar la capacidad de encontrar este tipo de cambio absoluto a través del modelado numérico, generalmente abandonando el álgebra lineal.
Los resultados fueron interesantes.
El experimento será pequeño: 4 monedas, 6 pares de monedas. Para cada par, una medida de curso.
Así que empecemos
La hipótesis es que el valor de cualquier moneda puede expresarse como un valor que tendrá en cuenta el valor de otras monedas en las que se cotiza, mientras que otras monedas se expresarán en el valor de todas las demás monedas. Esta es una tarea recursiva interesante.
Hay 4 monedas:
Para ellos, se marcaron los pares de divisas:
- eurusd
- gbpusd
- eurchf
- eurgbp
- gbpchf
- usdchf
Tenga en cuenta que si el número de monedas es n = 4, entonces el número de pares es k = (n ^ 2 - n) / 2 = 6. No tiene sentido buscar usdeur si se cotiza eurusd ...
En el tiempo t, se midió el tipo de cambio de uno de los proveedores:
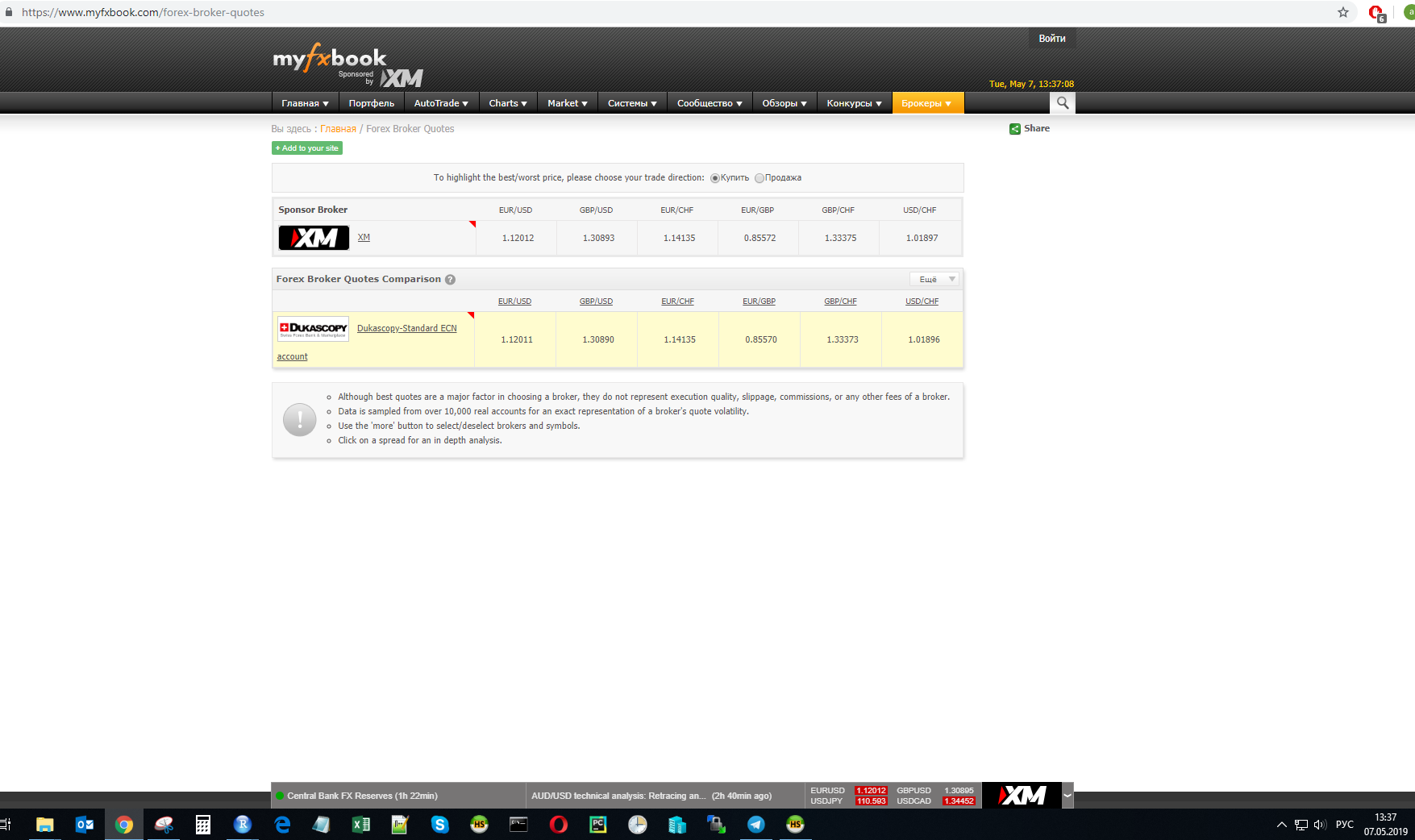
Se realizarán cálculos para estos valores.
Matemáticas
Resuelvo el problema tomando analíticamente el gradiente de la función de pérdida, que es esencialmente un sistema de ecuaciones.
El código del experimento estará en R:
R permite usar stats :: D para tomar una derivada de una función. Por ejemplo, si queremos diferenciar por la moneda USD, obtenemos la expresión:
2 * (eur / usd ^ 2 * (eurusd - eur / usd)) + 2 * (gbp / usd ^ 2 * (gbpusd -
gbp / usd)) - 2 * (1 / chf * (usdchf - usd / chf))
Para reducir el valor de la función express, realizaremos un descenso de gradiente e inmediatamente queda claro (vemos diferencias cuadradas) que el valor mínimo será cero, que es lo que necesitamos.
-deriv_vals * lr
El paso de descenso del gradiente será controlado por el parámetro lr y todo esto se toma con un signo negativo.
Es decir, en palabras humanas, seleccionamos las tasas de 4 monedas para que todos los pares de monedas en el experimento reciban valores iguales a los valores iniciales de estos pares. Mmm, resolvamos el rompecabezas, ¡en la frente!
Resultados
Para no estirar, le informaré de inmediato lo siguiente: el experimento en su conjunto fue exitoso, el código funcionó, el error se acercó, casi a cero. Pero luego noté que los resultados son siempre diferentes.
Una pregunta para los entendidos: parece que esta tarea tiene un número ilimitado de soluciones, pero en esto soy un cero completo, creo que me lo dirán en los comentarios.
Para verificar la (des) estabilidad de la solución, simulé 1000 veces sin fijar la semilla PRNG para los valores iniciales de los valores de moneda.
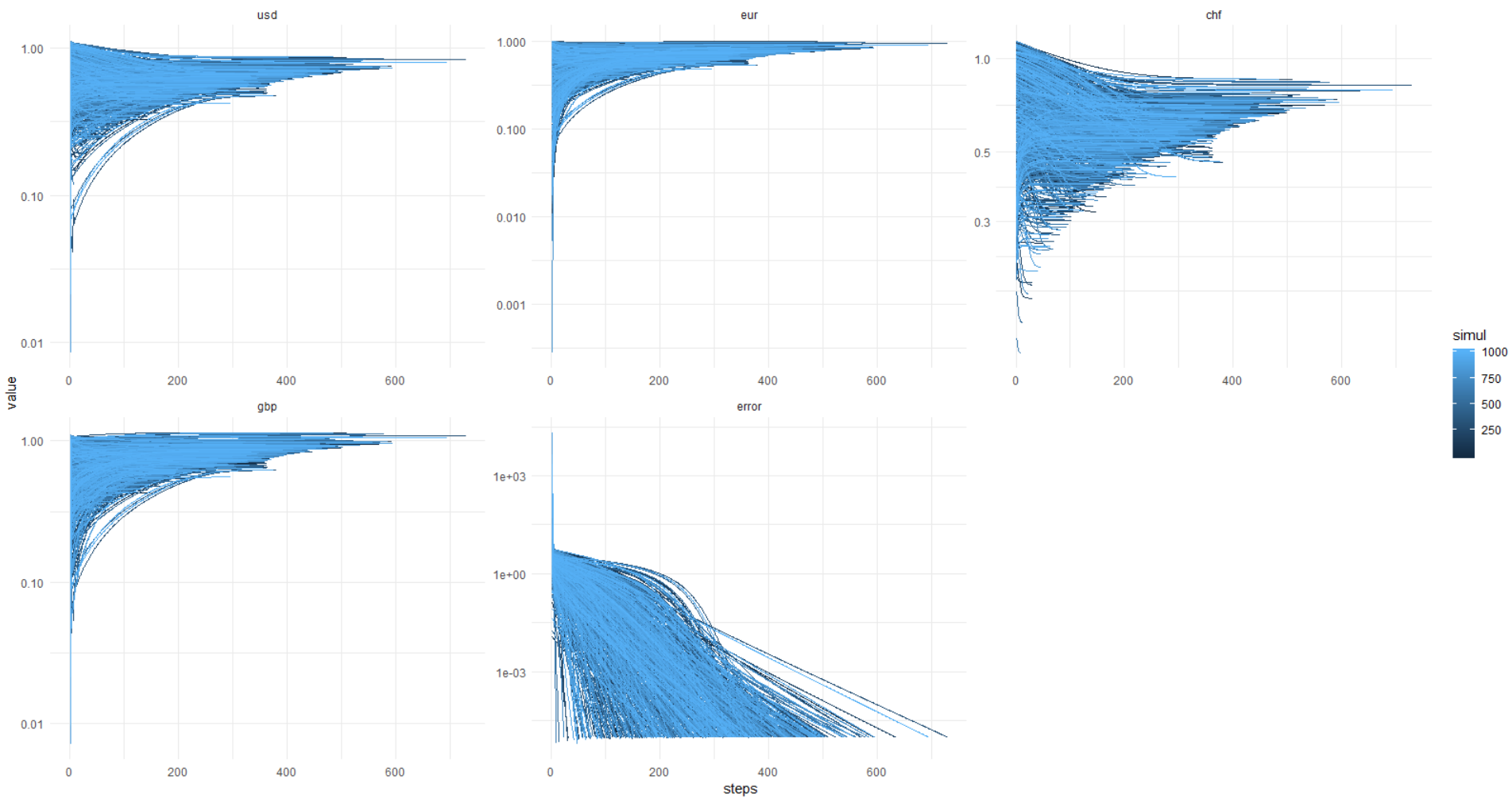
Y aquí viene la imagen del kata: el error alcanza 0.00001 y menos (la optimización se establece de esta manera) siempre, mientras que los valores de las monedas flotan en el diablo, sabe dónde. ¡Resulta que siempre hay una decisión diferente, caballeros!
Una vez más, esta imagen, eje y en las unidades originales (no log):
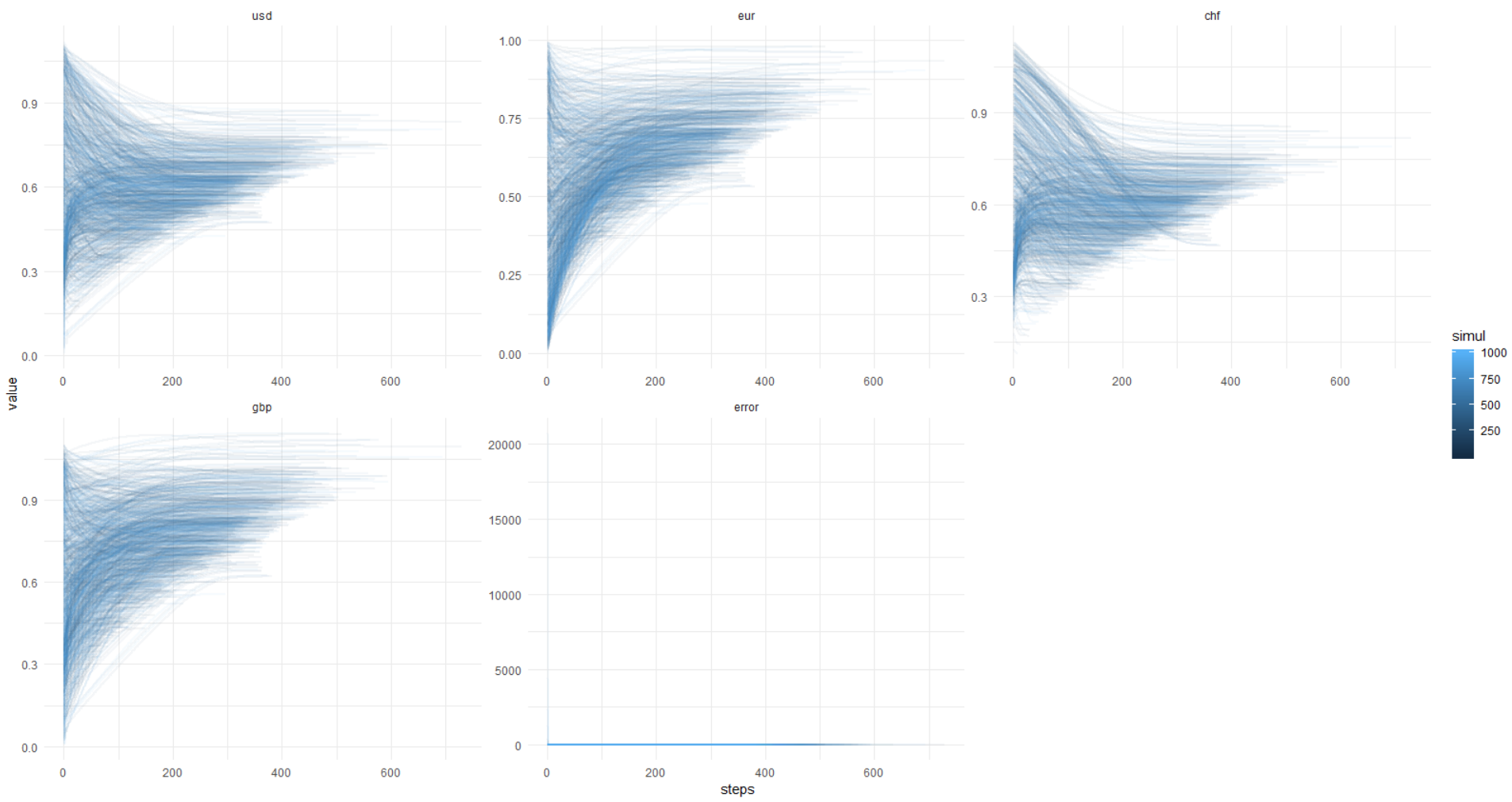
Para que pueda repetir esto, a continuación adjunto el código completo.
El código para 1000 simulaciones funciona durante aproximadamente un minuto.Conclusión
Esto es lo que no me queda claro:
- ¿Es posible estabilizar la solución de una manera matemática complicada?
- si habrá una convergencia con más monedas y pares de divisas;
- si no puede haber estabilidad, entonces, para cada nueva instantánea de datos, nuestras monedas caminarán como quieran, si no arregla la semilla PRNG, y esto es un fracaso.
Toda la idea parece muy vaga en ausencia de prerrequisitos y limitaciones inteligibles. ¡Pero fue interesante!
Bueno, también quería decir que puedes prescindir de OLS cuando los datos son complicados, las matrices son singulares, bueno, o cuando la teoría es poco conocida (ehh ...).
Gracias
eavprog por el mensaje inicial.
Adios